第3单元三位数乘两位数经典题型检测卷-数学四年级下册苏教版(含解析)
文档属性
| 名称 | 第3单元三位数乘两位数经典题型检测卷-数学四年级下册苏教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 365.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-02 21:59:53 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第3单元三位数乘两位数经典题型检测卷-数学四年级下册苏教版
一、选择题
1.已知a×b=c,且a和b都比300小,那么c最大是( )。
A.四位数 B.五位数 C.六位数
2.625乘35的积比325乘65的积( )。
A.大 B.小 C.相等
3.若△×430=☆×260(△和☆均不为0),△与☆比较,( )。
A.△<☆ B.△>☆ C.不能确定
4.( )组中两道算式的得数相等。
A.32×120和32×12 B.45×730和540×73 C.960×40和96×400
5.246×75,乘数十位上的7乘246得( )。
A.1722 B.17220 C.172200
6.楚源小区有15栋楼房,每栋有120户人家,小区共有( )户人家。
A.1800 B.1500 C.2000
二、填空题
7.的积的个位是( ),的积是( )位数。
8.333乘一个两位数,积是一个四位数,这个两位数最大是( )。
9.在( )里填“>”“<”或“=”。
①320×1( )150×32 ②37×402( )501×37
③230×15( )230×17 ④99999( )100000
⑤36080000( )999万 ⑥10个十万( )100万
10.找规律填数。
1+121×9=1090
2+232×9=2090
3+343×9=3090
4+( )×9=4090
( )+( )×9=7090
11.已知a×b=c,(a×10)×(b×10)=c×( );已知a÷b=c,(a÷d)÷(b÷d)=( )(b和d均不为0)。
12.两个数相乘的积是68,如果一个因数乘3,另一个因数不变,现在的积是( )。
三、判断题
13.在计算208×17时,乘数中间的0可以不乘。( )
14.两数相乘,一个乘数不变,另一个乘数扩大几倍,积也扩大几倍。( )
15.25×4=100,25×12=300。( )
16.我国古代劳动人民创造的“铺地锦”的方法,可以计算两位数或三位数乘两位数。( )
17.小明骑车的速度是15千米/小时,小华骑车的速度是250米/分钟,小华速度快。( )
四、计算题
18.口算。
1200÷40= 200×35= 510÷30= 15×600=
7200÷6= 640÷4= 400÷50= 400×20=
19.用竖式计算。
①208×36= ②50×980= ③67×289=
五、解答题
20.王爷爷家有116棵槐树,去年平均每棵树收获槐米47千克。今年预计每棵比去年多收获20千克,今年预计一共能收获槐米多少千克?
21.商店购进44台复读机,每台320元,已经按原价卖出31台,剩下的按现价出售,如果所有的复读机全部售出,这家商店是赚了还是赔了?
22.一只山雀5天大约能吃800只害虫,照这样计算,一只山雀一个月大约能吃多少只害虫?(一个月按30天计算)
23.张老师买来500毫升装的饮料16瓶,共花了48元。平均每瓶饮料多少元?张老师一共买来多少升饮料?
24.一份稿件有5300个字,红红平均每分钟能打120个字,她45分钟能打完吗?
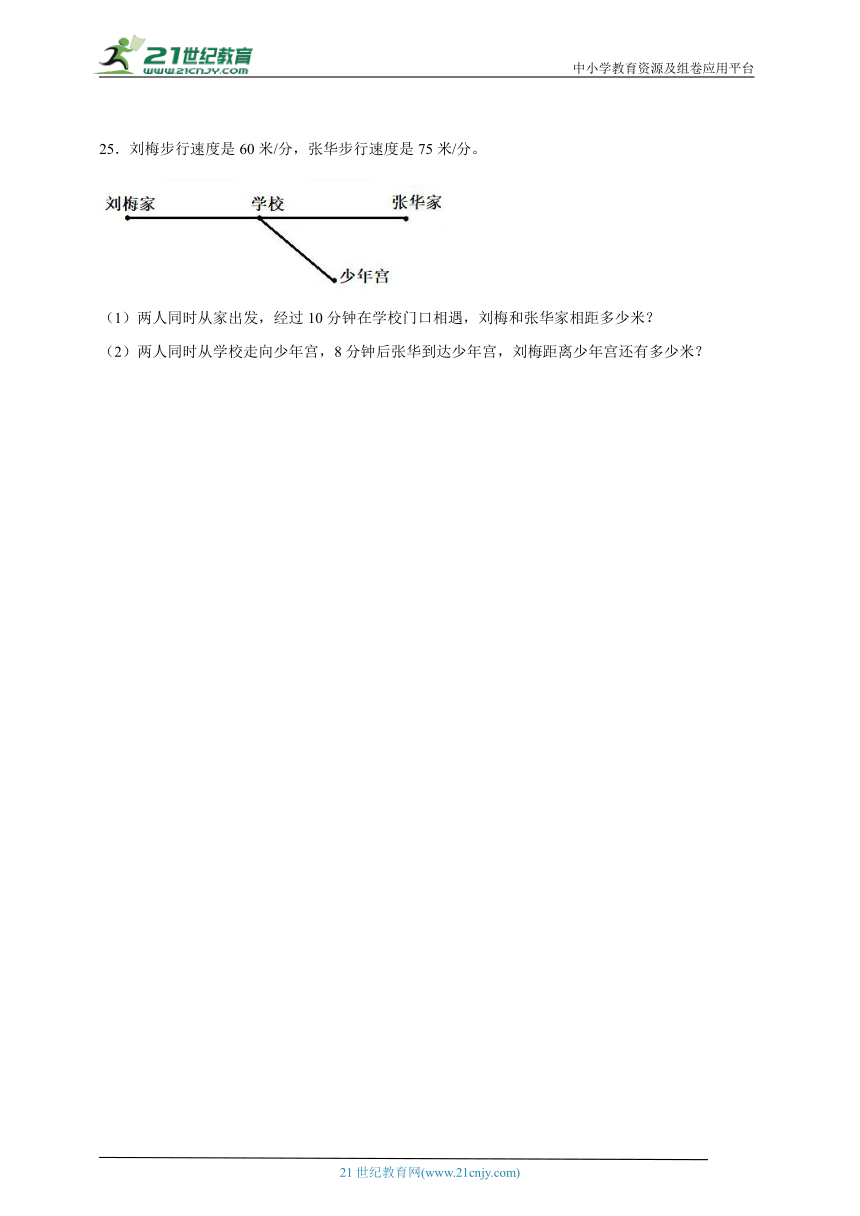
25.刘梅步行速度是60米/分,张华步行速度是75米/分。
(1)两人同时从家出发,经过10分钟在学校门口相遇,刘梅和张华家相距多少米?
(2)两人同时从学校走向少年宫,8分钟后张华到达少年宫,刘梅距离少年宫还有多少米?
参考答案:
1.B
【分析】从题意中知道要求c最大是几位数,c最大时,a和b也得最大。a和b都比300小,那么最大是299,299×299=89401。
【详解】299×299=89401,积是五位数。已知a×b=c,且a和b都比300小,那么c最大是五位数。
故答案为:B
【点睛】当算式中都是字母时,可以通过举例子的方法进行解题,把a,b,c当作数通过计算出数值来确认最终答案。
2.A
【解析】先求出两个数的积,再进行比较来选择。
【详解】625×35=21875,325×65=21125,21875>21125。
故答案为:A
【点睛】考查学生对三位数乘两位数的计算掌握情况。
3.A
【解析】因为△×430=☆×260(△和☆均不为0),430>260,一个因数变小,要使积不变,另一个因数需要变大,由此解答。
【详解】△×430=☆×260(△和☆均不为0)
430>260
△<☆
故答案为:A
【点睛】解答本题的关键是明白:要使积不变,一个因数变小,另一个因数需要变大。
4.C
【分析】根据整数乘法的计算方法,分别计算出结果后即可判断。
【详解】A. 32×120=3840,32×12=384
B. 45×730=32850,540×73=39420
C. 960×40=38400,96×400=38400
故答案为:C
【点睛】解答本题的关键是熟练掌握整数乘法的计算方法,本题也可根据积的变化规律解答。
5.B
【解析】根据三位数乘两位数的计算方法,两位数十位数上的数是几,表示几个十,去乘三位数,表示几个十去乘三位数,由此计算即可。
【详解】十位上的7表示7个十;
246×70=17220
故答案为:B
【点睛】解答本题的关键是要正确理解三位数乘两位数的每一步的意义,对算理要能充分理解。
6.A
【解析】根据题意,可知每栋有120户人家,小区内有15栋楼房,就有15个120户,即120×15就是要求的结果。
【详解】120×15=1800(户)
答:小区共有1800户人家。
故答案为:A
【点睛】理解好题意,找清它们之间的关系,是解决此类问题的关键,然后再进一步解答即可。
7. 7 五
【分析】根据三位数乘两位数的计算方法,求出的积,再判断积个位上的数。先求出的积,再判断积的位数。
【详解】,19027个位是7;
,11250的积是五位数。
【点睛】熟练掌握三位数乘两位数的计算方法并正确计算是解决本题的关键。
8.30
【分析】根据三位数乘整十数的口算方法,333×30=9990,再计算333×31的积,若积是五位数,则这个两位数最大是30;若积不是五位数,则继续计算333×32,若积是五位数,则这个两位数最大是31;若积不是五位数,则继续计算333×33;依次类推。
【详解】
所以这个两位数最大是30。
【点睛】熟练掌握三位数乘两位数的计算方法是解答此题的关键。
9. < < < < > =
【分析】①:根据积不变的规律把320×1变换成32×10,然后比较大小;
②③:一个因数相同,另一个因数大的积就大;
④:五位数小于六位数;
⑤:把999万写成9990000,然后比较大小;
⑥:10个十万就是一百万,也就是100万。
【详解】320×1=32×10,所以320×1<150×32;
402<501,所以37×402<501×37;
15<17,所以230×15<230×17;
99999<100000;
999万=9990000,36080000>999万;
10个十万=100万。
【点睛】此题重点考查整数大小比较和积的变化规律的灵活运用。
10. 454 7 787
【分析】观察这组算式可知,第一个加数与第一个因数百位和个位上的数字相同,第一个因数十位上的数字比第一个加数多1,第二个因数是9,而积是一个四位数,个位和百位是0.十位是9,千位上的数和第一个加数相同,据此解答。
【详解】1+121×9=1090
2+232×9=2090
3+343×9=3090
4+454×9=4090
7+787×9=7090
【点睛】根据已知的算式得出算式之间的变化关系和规律,然后利用这个变化规律解决问题。
11. 100 c
【分析】(1)乘法算式中,一个因数扩大a倍,一个因数扩大b倍,积就扩大a×b倍。
(2)商不变的规律:被除数和除数同时乘或除以相同的数(0除外),商不变。
【详解】已知a×b=c,(a×10)×(b×10)=c×100;
已知a÷b=c,(a÷d)÷(b÷d)=c(b和d均不为0)。
【点睛】熟练掌握积的变化规律与商不变的规律,是解答此题的关键。
12.204
【分析】积的变化规律:两个数相乘,一个因数不变,另一个因数乘几或除以几(0除外),积也乘几或除以相同的数。
【详解】根据积的变化规律可知:两个数相乘的积是68,如果一因数乘3,另一个因数不变,现在的积是68×3=204。
【点睛】熟练掌握积的变化规律是解答此题的关键。
13.×
【分析】本题根据整数乘法的运算法则进行分析判断即可。
【详解】在计算整数乘法时,从右起,依次用第二个因数每位上的数去乘第一个因数,乘到哪一位,得数的末尾就和第二个因数的哪一位对齐,即乘数中间有0,也同样要乘。
故答案为:×
【点睛】该题要求学生熟练掌握整数乘法的运算法则,特别是乘数末尾有0和中间有0的区别。
14.√
【分析】根据积的变化规律:一个因数不变,另一个因数扩大或缩小多少倍(0除外),积也会随着扩大或缩小相同的倍数。
【详解】两个数相乘,一个因数不变,另一个因数扩大几倍,积也扩大几倍。
如:2×10=20,2×100=200,一个因数不变,另一个因数扩大10倍,积也扩大10倍。
故答案为:√
【点睛】本题主要考查了学生对积的变化规律的掌握情况。
15.√
【分析】根据积的变化规律:一个因数不变,另一个因数扩大几倍,积也扩大相同的倍数。
【详解】25×4=100;
4×3=12;
100×3=300;
所以,25×12=300
故答案为:√
【点睛】本题主要考查积的变化规律,关键是通过观察数据进行巧算。
16.√
【分析】“铺地锦”方法:先画一个矩形,把它分成m×n个方格(m,n分别为两乘数的位数),在方格上边、右边分别写下两个因数;再用对角线把方格一分为二,分别记录上述各位数字相应乘积的十位数与个位数,然后这些乘积由右下到左上,沿斜线方向相加,相加满十时向前进一,最后得到结果(方格左侧与下方数字依次排列),据此判断。
【详解】由分析知:
如:26×73=1898
487×34=16558
所以判断正确。
故答案为:√
【点睛】本题主要考查了学生对“铺地锦”法的掌握情况。
17.×
【分析】小明骑车的速度是15千米/小时,则小明1小时行驶15千米。小华骑车的速度是250米/分钟,则小华1小时行驶250×60米。千米和米之间的进率是1000,据此将小华1小时行驶的路程换算成千米,再和15千米比较大小。
【详解】250×60=15000(米)=15(千米)
则小华1小时行驶15千米,与小明骑车的速度是同样大的。
故答案为:×。
【点睛】本题考查行程问题,要判断两个人的速度大小,应分别求出同样时间内行驶的路程,再进行比较。
18.30;7000;17;9000;
1200;160;8;8000
【详解】略
19.7488;49000;19363
【分析】三位数乘两位数时,用第二个因数每一位上的数分别去乘第一个因数,然后把各次乘得的数加起来。
【详解】①208×36=7488 ②50×980=49000 ③67×289=19363
20.7772千克
【分析】首先求出今年平均每棵收获槐米多少千克,然后根据乘法的意义,用求出今年平均每棵收获槐米的重量乘王爷爷家槐树的数量,求出今年预计收获槐米多少千克即可。
【详解】(47+20)×116
=67×116
=7772(千克)
答:今年预计一共能收获槐米7772千克。
【点睛】此题主要考查了加法、乘法的意义的应用,解答此题的关键是求出今年平均每棵收获槐米多少千克。
21.赚了
【分析】用44乘320求出44台的进购价;用31乘400求出31台卖了多少元,剩下44-31=13台,用13乘220求出13台卖了多少元,然后把31台和13台卖的价钱相加,最后相加的和与44台的进购价相比,据此解答。
【详解】320×44=14080(元)
400×31+220×(44-31)
=12400+220×13
=12400+2860
=15260(元)
15260>14080
答:这家商店赚了。
【点睛】解答此题的关键是求出进购价、总的售价;最后两者相比较。
22.4800只
【分析】先用800除以5计算出一只山雀1天大约能吃害虫的数量,然后用一只山雀1天大约能吃害虫的数量乘30即可,依此计算。
【详解】800÷5=160(只)
160×30=4800(只)
答:一只山雀一个月大约能吃4800只害虫。
【点睛】此题考查的是归一问题的计算,先计算出一只山雀1天大约能吃害虫的数量是解答此题的关键。
23.3元;8升
【分析】16瓶饮料花了48元钱,用除法可以计算出一瓶饮料的价格;16瓶500毫升装的饮料,用乘法可以求出一共多少毫升;根据升和毫升的进率,可以换算出共有多少升饮料。
【详解】48÷16=3(元)
500×16=8000(毫升)
8000毫升=8升
答:平均每瓶饮料3元;张老师一共买来8升饮料。
【点睛】本题考查的是整数的乘法和除法的应用以及升与毫升的进率换算。
24.能
【分析】用每分钟打字字数乘打字时间,求出打字总字数。再和稿件字数比较大小。
【详解】120×45=5400(个)
5300<5400
答:她45分钟能打完。
【点睛】熟练掌握三位数乘两位数的计算方法并正确计算是解决本题的关键。
25.(1)1350米
(2)120米
【分析】(1)两人的速度和乘行走的时间即可解答。
(2)两人的速度差乘行走的时间即可解答。
【详解】(1)(60+75)×10
=135×10
=1350(米)
答:刘梅和张华家相距1350米。
(2)(75-60)×8
=15×8
=120(米)
答:刘梅距离少年宫还有120米。
【点睛】熟练掌握路程、速度和时间三者之间的关系是解答本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第3单元三位数乘两位数经典题型检测卷-数学四年级下册苏教版
一、选择题
1.已知a×b=c,且a和b都比300小,那么c最大是( )。
A.四位数 B.五位数 C.六位数
2.625乘35的积比325乘65的积( )。
A.大 B.小 C.相等
3.若△×430=☆×260(△和☆均不为0),△与☆比较,( )。
A.△<☆ B.△>☆ C.不能确定
4.( )组中两道算式的得数相等。
A.32×120和32×12 B.45×730和540×73 C.960×40和96×400
5.246×75,乘数十位上的7乘246得( )。
A.1722 B.17220 C.172200
6.楚源小区有15栋楼房,每栋有120户人家,小区共有( )户人家。
A.1800 B.1500 C.2000
二、填空题
7.的积的个位是( ),的积是( )位数。
8.333乘一个两位数,积是一个四位数,这个两位数最大是( )。
9.在( )里填“>”“<”或“=”。
①320×1( )150×32 ②37×402( )501×37
③230×15( )230×17 ④99999( )100000
⑤36080000( )999万 ⑥10个十万( )100万
10.找规律填数。
1+121×9=1090
2+232×9=2090
3+343×9=3090
4+( )×9=4090
( )+( )×9=7090
11.已知a×b=c,(a×10)×(b×10)=c×( );已知a÷b=c,(a÷d)÷(b÷d)=( )(b和d均不为0)。
12.两个数相乘的积是68,如果一个因数乘3,另一个因数不变,现在的积是( )。
三、判断题
13.在计算208×17时,乘数中间的0可以不乘。( )
14.两数相乘,一个乘数不变,另一个乘数扩大几倍,积也扩大几倍。( )
15.25×4=100,25×12=300。( )
16.我国古代劳动人民创造的“铺地锦”的方法,可以计算两位数或三位数乘两位数。( )
17.小明骑车的速度是15千米/小时,小华骑车的速度是250米/分钟,小华速度快。( )
四、计算题
18.口算。
1200÷40= 200×35= 510÷30= 15×600=
7200÷6= 640÷4= 400÷50= 400×20=
19.用竖式计算。
①208×36= ②50×980= ③67×289=
五、解答题
20.王爷爷家有116棵槐树,去年平均每棵树收获槐米47千克。今年预计每棵比去年多收获20千克,今年预计一共能收获槐米多少千克?
21.商店购进44台复读机,每台320元,已经按原价卖出31台,剩下的按现价出售,如果所有的复读机全部售出,这家商店是赚了还是赔了?
22.一只山雀5天大约能吃800只害虫,照这样计算,一只山雀一个月大约能吃多少只害虫?(一个月按30天计算)
23.张老师买来500毫升装的饮料16瓶,共花了48元。平均每瓶饮料多少元?张老师一共买来多少升饮料?
24.一份稿件有5300个字,红红平均每分钟能打120个字,她45分钟能打完吗?
25.刘梅步行速度是60米/分,张华步行速度是75米/分。
(1)两人同时从家出发,经过10分钟在学校门口相遇,刘梅和张华家相距多少米?
(2)两人同时从学校走向少年宫,8分钟后张华到达少年宫,刘梅距离少年宫还有多少米?
参考答案:
1.B
【分析】从题意中知道要求c最大是几位数,c最大时,a和b也得最大。a和b都比300小,那么最大是299,299×299=89401。
【详解】299×299=89401,积是五位数。已知a×b=c,且a和b都比300小,那么c最大是五位数。
故答案为:B
【点睛】当算式中都是字母时,可以通过举例子的方法进行解题,把a,b,c当作数通过计算出数值来确认最终答案。
2.A
【解析】先求出两个数的积,再进行比较来选择。
【详解】625×35=21875,325×65=21125,21875>21125。
故答案为:A
【点睛】考查学生对三位数乘两位数的计算掌握情况。
3.A
【解析】因为△×430=☆×260(△和☆均不为0),430>260,一个因数变小,要使积不变,另一个因数需要变大,由此解答。
【详解】△×430=☆×260(△和☆均不为0)
430>260
△<☆
故答案为:A
【点睛】解答本题的关键是明白:要使积不变,一个因数变小,另一个因数需要变大。
4.C
【分析】根据整数乘法的计算方法,分别计算出结果后即可判断。
【详解】A. 32×120=3840,32×12=384
B. 45×730=32850,540×73=39420
C. 960×40=38400,96×400=38400
故答案为:C
【点睛】解答本题的关键是熟练掌握整数乘法的计算方法,本题也可根据积的变化规律解答。
5.B
【解析】根据三位数乘两位数的计算方法,两位数十位数上的数是几,表示几个十,去乘三位数,表示几个十去乘三位数,由此计算即可。
【详解】十位上的7表示7个十;
246×70=17220
故答案为:B
【点睛】解答本题的关键是要正确理解三位数乘两位数的每一步的意义,对算理要能充分理解。
6.A
【解析】根据题意,可知每栋有120户人家,小区内有15栋楼房,就有15个120户,即120×15就是要求的结果。
【详解】120×15=1800(户)
答:小区共有1800户人家。
故答案为:A
【点睛】理解好题意,找清它们之间的关系,是解决此类问题的关键,然后再进一步解答即可。
7. 7 五
【分析】根据三位数乘两位数的计算方法,求出的积,再判断积个位上的数。先求出的积,再判断积的位数。
【详解】,19027个位是7;
,11250的积是五位数。
【点睛】熟练掌握三位数乘两位数的计算方法并正确计算是解决本题的关键。
8.30
【分析】根据三位数乘整十数的口算方法,333×30=9990,再计算333×31的积,若积是五位数,则这个两位数最大是30;若积不是五位数,则继续计算333×32,若积是五位数,则这个两位数最大是31;若积不是五位数,则继续计算333×33;依次类推。
【详解】
所以这个两位数最大是30。
【点睛】熟练掌握三位数乘两位数的计算方法是解答此题的关键。
9. < < < < > =
【分析】①:根据积不变的规律把320×1变换成32×10,然后比较大小;
②③:一个因数相同,另一个因数大的积就大;
④:五位数小于六位数;
⑤:把999万写成9990000,然后比较大小;
⑥:10个十万就是一百万,也就是100万。
【详解】320×1=32×10,所以320×1<150×32;
402<501,所以37×402<501×37;
15<17,所以230×15<230×17;
99999<100000;
999万=9990000,36080000>999万;
10个十万=100万。
【点睛】此题重点考查整数大小比较和积的变化规律的灵活运用。
10. 454 7 787
【分析】观察这组算式可知,第一个加数与第一个因数百位和个位上的数字相同,第一个因数十位上的数字比第一个加数多1,第二个因数是9,而积是一个四位数,个位和百位是0.十位是9,千位上的数和第一个加数相同,据此解答。
【详解】1+121×9=1090
2+232×9=2090
3+343×9=3090
4+454×9=4090
7+787×9=7090
【点睛】根据已知的算式得出算式之间的变化关系和规律,然后利用这个变化规律解决问题。
11. 100 c
【分析】(1)乘法算式中,一个因数扩大a倍,一个因数扩大b倍,积就扩大a×b倍。
(2)商不变的规律:被除数和除数同时乘或除以相同的数(0除外),商不变。
【详解】已知a×b=c,(a×10)×(b×10)=c×100;
已知a÷b=c,(a÷d)÷(b÷d)=c(b和d均不为0)。
【点睛】熟练掌握积的变化规律与商不变的规律,是解答此题的关键。
12.204
【分析】积的变化规律:两个数相乘,一个因数不变,另一个因数乘几或除以几(0除外),积也乘几或除以相同的数。
【详解】根据积的变化规律可知:两个数相乘的积是68,如果一因数乘3,另一个因数不变,现在的积是68×3=204。
【点睛】熟练掌握积的变化规律是解答此题的关键。
13.×
【分析】本题根据整数乘法的运算法则进行分析判断即可。
【详解】在计算整数乘法时,从右起,依次用第二个因数每位上的数去乘第一个因数,乘到哪一位,得数的末尾就和第二个因数的哪一位对齐,即乘数中间有0,也同样要乘。
故答案为:×
【点睛】该题要求学生熟练掌握整数乘法的运算法则,特别是乘数末尾有0和中间有0的区别。
14.√
【分析】根据积的变化规律:一个因数不变,另一个因数扩大或缩小多少倍(0除外),积也会随着扩大或缩小相同的倍数。
【详解】两个数相乘,一个因数不变,另一个因数扩大几倍,积也扩大几倍。
如:2×10=20,2×100=200,一个因数不变,另一个因数扩大10倍,积也扩大10倍。
故答案为:√
【点睛】本题主要考查了学生对积的变化规律的掌握情况。
15.√
【分析】根据积的变化规律:一个因数不变,另一个因数扩大几倍,积也扩大相同的倍数。
【详解】25×4=100;
4×3=12;
100×3=300;
所以,25×12=300
故答案为:√
【点睛】本题主要考查积的变化规律,关键是通过观察数据进行巧算。
16.√
【分析】“铺地锦”方法:先画一个矩形,把它分成m×n个方格(m,n分别为两乘数的位数),在方格上边、右边分别写下两个因数;再用对角线把方格一分为二,分别记录上述各位数字相应乘积的十位数与个位数,然后这些乘积由右下到左上,沿斜线方向相加,相加满十时向前进一,最后得到结果(方格左侧与下方数字依次排列),据此判断。
【详解】由分析知:
如:26×73=1898
487×34=16558
所以判断正确。
故答案为:√
【点睛】本题主要考查了学生对“铺地锦”法的掌握情况。
17.×
【分析】小明骑车的速度是15千米/小时,则小明1小时行驶15千米。小华骑车的速度是250米/分钟,则小华1小时行驶250×60米。千米和米之间的进率是1000,据此将小华1小时行驶的路程换算成千米,再和15千米比较大小。
【详解】250×60=15000(米)=15(千米)
则小华1小时行驶15千米,与小明骑车的速度是同样大的。
故答案为:×。
【点睛】本题考查行程问题,要判断两个人的速度大小,应分别求出同样时间内行驶的路程,再进行比较。
18.30;7000;17;9000;
1200;160;8;8000
【详解】略
19.7488;49000;19363
【分析】三位数乘两位数时,用第二个因数每一位上的数分别去乘第一个因数,然后把各次乘得的数加起来。
【详解】①208×36=7488 ②50×980=49000 ③67×289=19363
20.7772千克
【分析】首先求出今年平均每棵收获槐米多少千克,然后根据乘法的意义,用求出今年平均每棵收获槐米的重量乘王爷爷家槐树的数量,求出今年预计收获槐米多少千克即可。
【详解】(47+20)×116
=67×116
=7772(千克)
答:今年预计一共能收获槐米7772千克。
【点睛】此题主要考查了加法、乘法的意义的应用,解答此题的关键是求出今年平均每棵收获槐米多少千克。
21.赚了
【分析】用44乘320求出44台的进购价;用31乘400求出31台卖了多少元,剩下44-31=13台,用13乘220求出13台卖了多少元,然后把31台和13台卖的价钱相加,最后相加的和与44台的进购价相比,据此解答。
【详解】320×44=14080(元)
400×31+220×(44-31)
=12400+220×13
=12400+2860
=15260(元)
15260>14080
答:这家商店赚了。
【点睛】解答此题的关键是求出进购价、总的售价;最后两者相比较。
22.4800只
【分析】先用800除以5计算出一只山雀1天大约能吃害虫的数量,然后用一只山雀1天大约能吃害虫的数量乘30即可,依此计算。
【详解】800÷5=160(只)
160×30=4800(只)
答:一只山雀一个月大约能吃4800只害虫。
【点睛】此题考查的是归一问题的计算,先计算出一只山雀1天大约能吃害虫的数量是解答此题的关键。
23.3元;8升
【分析】16瓶饮料花了48元钱,用除法可以计算出一瓶饮料的价格;16瓶500毫升装的饮料,用乘法可以求出一共多少毫升;根据升和毫升的进率,可以换算出共有多少升饮料。
【详解】48÷16=3(元)
500×16=8000(毫升)
8000毫升=8升
答:平均每瓶饮料3元;张老师一共买来8升饮料。
【点睛】本题考查的是整数的乘法和除法的应用以及升与毫升的进率换算。
24.能
【分析】用每分钟打字字数乘打字时间,求出打字总字数。再和稿件字数比较大小。
【详解】120×45=5400(个)
5300<5400
答:她45分钟能打完。
【点睛】熟练掌握三位数乘两位数的计算方法并正确计算是解决本题的关键。
25.(1)1350米
(2)120米
【分析】(1)两人的速度和乘行走的时间即可解答。
(2)两人的速度差乘行走的时间即可解答。
【详解】(1)(60+75)×10
=135×10
=1350(米)
答:刘梅和张华家相距1350米。
(2)(75-60)×8
=15×8
=120(米)
答:刘梅距离少年宫还有120米。
【点睛】熟练掌握路程、速度和时间三者之间的关系是解答本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
