子集(江苏省徐州市)

课件12张PPT。子集、全集、补集数学理论子集的概念
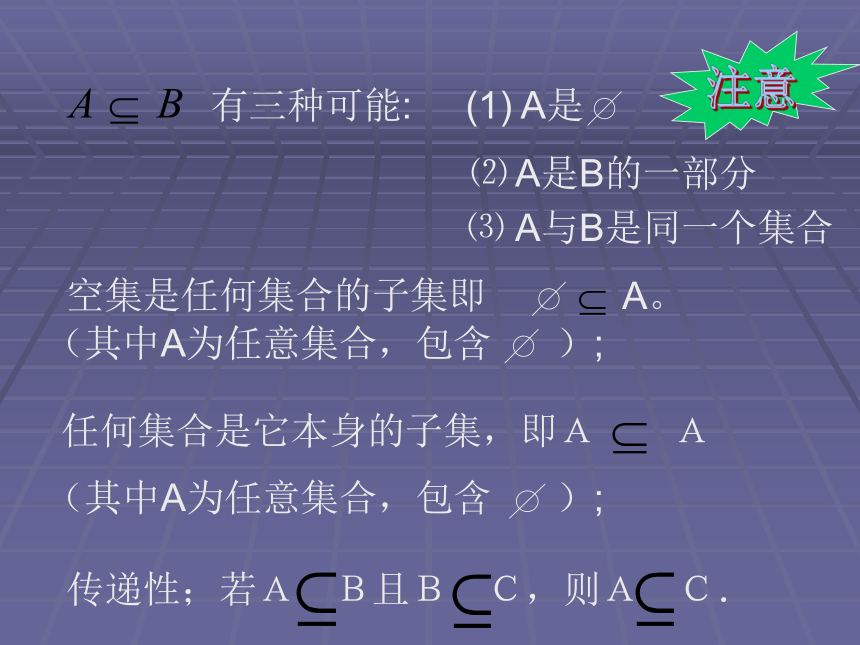
如果集合A中的任意一个元素都是集合B中的元素（若a∈A，则a∈B），那么集合A叫做集合B的子集（subset），记作A?B或B? A，读作“集合A包含于集合B”或“集合B包含集合A”.
B A传递性；若Ａ　Ｂ且Ｂ　Ｃ，则Ａ　Ｃ．数学运用例1、写出集合{a, b}的所有子集， 集合 {1,2,3}的所有子集.
解：集合{a, b}的所有子集是Φ, {a}, {b}, {a, b}.
集合{1，2，3}的所有子集是Φ， {1},{2},{3},{1,2},
{1,3},{2,3},{1,2,3}.
集合{a1,a2,a3,a4}有多少子集？数学理论、数学运用真子集的概念
对于两个集合A与B,如果A?B ，并且A≠B 则称集合A为集合B的真子集．记A B或B 　A读作“集合A真包含于集合B”或“集合B真包含集合A”.例1、写出集合{a,b}的所有真子集， 集合{1,2,3}的所有真子集.数学运用略解：⑴Φ，{4}，{1，4}，{4，5}.
⑵{1，2，3}，{1，2，3，4}，{1，2，3，5}
⑶①若3=x+2,则x=1,此时x2=1，与互异性矛盾，舍去；
②若x2=x+2，则x=-1（舍）x=2(符合) .数学理论补集的概念思考：观察例3中每一组的3个集合，它们之间还有什么
关系？ 例3、（1）S={-2,-1,1,2},A={-1,1},B={-2,2};
（2）S=R,A={x|x≤0,x∈R}，B={x|x>0, x∈R };
（3）S={x|x为地球人}，A={x|x为中国人}，B={x|x为外国人}.设A S，由S中不属于A的所有元素组成的集合称为S的
子集A的补集（complementary set),记为?SA={x|x∈S，
且x S}.?SA可用阴影部分表示，如图对于例3，我们有B=?SA, A=?SB.数学理论 、数学运用如果集合S包含我们所要研究的各个集合，这时S
可以看作一个全集（universal set）,全集通常
记作U.如在实数集范围内讨论集合时，R便可看
作一个全集.注：（1）补集是相对全集而言，离开全集谈补集
没有意义；
（2）B=?SA, 则A=?SB，即?S(?SA )=A；
（3）Φ=?SS, S=?SΦ.全集的概念数学运用例 、⑴已知全集U，集合A={1，3，5，7，9}，
?UA={2，4，6，8}，?UB={1，4，6，8，9}，求集合B；
⑵已知全集U={2，4，a2-a+1},B={a+1,2},若?UB={7}，
求实数a的值.答：⑴B={2，3，5，7}.
⑵a=3.回顾反思
本节课我们学习了子集、全集、补集的概念，认识了两集合之间的关系，初步掌握了补集的求法以及利用子集、补集的定义来处理相关的问题.课堂练习1已知集合A＝{x|x2＋ax＋1＝0}，B＝{1,2}，且A?B，求a的取值范围.
2 已知集合A＝{1，3，a}，Ｂ＝{1，a2－a＋ 1}若B?A，求a的值.
3 已知全集U＝{1，2，3，4，5}，A＝{x|x2
－5x＋q＝0}，求?UA及q的值.
再见