第4单元比例高频考点检测卷-数学六年级下册人教版(含解析)
文档属性
| 名称 | 第4单元比例高频考点检测卷-数学六年级下册人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 489.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-03 14:16:11 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第4单元比例高频考点检测卷-数学六年级下册人教版
一、选择题
1.如果5a=7b,下列式子正确的是( )。
A.5∶b=7∶a B.a∶b=5∶7 C.b∶a=7∶5 D.5∶a=7∶b
2.以下哪个不成正比例( )。
A.长方形的宽一定,面积和长 B.汽车的速度一定,总路程和时间
C.被减数一定,减数和差 D.除数一定,被除数和商
3.下列各关系中,成正比例关系的是( )。
A.全班人数一定,出勤人数和缺勤人数 B.货物总量一定,每天运送的吨数和所需天数
C.总价一定,数量和单价 D.水稻每公顷产量一定,水稻的总产量与公顷数
4.如果按1∶1000的比例尺制作一个中央广播电视塔模型(包括避雷针),高为40.5cm。中央广播电视塔的实际总高度是( )米。
A.4.05 B.40.5 C.405 D.4050
5.一个零件长5毫米,在设计图纸上的长度是20厘米,图纸的比例尺是( )。
A.1∶4 B.4∶1 C.1∶40 D.40∶1
6.把一个长10cm、宽6cm的长方形按3∶1放大,得到的图形的面积是( )。
A. B. C. D.
二、填空题
7.根据4.5×4=3.6×5写出一个比例是( )。
8.如果5=6,那么和成( )比例;如果∶3=5∶,那么和成( )比例。
9.东东沿着直尺的方向将橡皮筋拉紧(如图,AC是橡皮筋示意图,B是橡皮筋上的一点)。如果点A的位置固定不变,沿着原来的方向将橡皮筋拉长,使点C的位置在15cm处,此时点B的位置在( )cm处。
10.在比例尺的地图上。1厘米表示实际距离( )千米,实际距离420千米,在这幅地图上用( )厘米表示。
11.小华身高1.6米,在照片上她的身高是5厘米,这张照片的比例尺是( );在一幅比例尺是1∶500的图纸上,量得一个圆形草坪的直径是4厘米,这个草坪的实际面积是( )平方米。
12.为了庆祝六一节每张卡片减价20%,用同样多的钱可以多买6张,原来可以买( )张卡片。
三、判断题
13.如果,那么和一定互为倒数。( )
14.一个5mm长零件画在图纸上的长是20cm,这幅图的比例尺是1∶40。( )
15.汽车的速度和时间成反比例关系。( )
16.如果a×3=b×5(a、b均不为0),那么a∶b=3∶5。( )
17.a和b都不为0,a×=b×,那么a>b。( )
四、计算题
18.应用比例的基本性质,判断下面哪几组的两个比可以组成比例。把组成的比例写出来。
(1)和 (2)和
(3)和 (4)和
19.解方程或比例。
① ② ③
五、解答题
20.化肥厂生产一批化肥,每天生产30吨,50天完成。如果要40天完成任务,每天应多生产多少吨?(用比例解)
21.在比例尺为1∶6000000的地图上量得A、B两地相距8厘米,一辆货车以每小时80千米的速度从A地开往B地。需要多少小时到达?
22.一种稀释消毒液,用药液和水按1∶120配制而成。要配制这种稀释消毒液605千克,需要药液多少千克?(用比例知识解答)
23.按要求完成下列各题。
(1)将这幅平面图的线段比例尺转化成数值比例尺是( )。
(2)邮局在学校的( ),相距( )m。
(3)少年宫在学校的西偏北30°方向上250m处,请按给定的比例尺画出少年宫的位置。
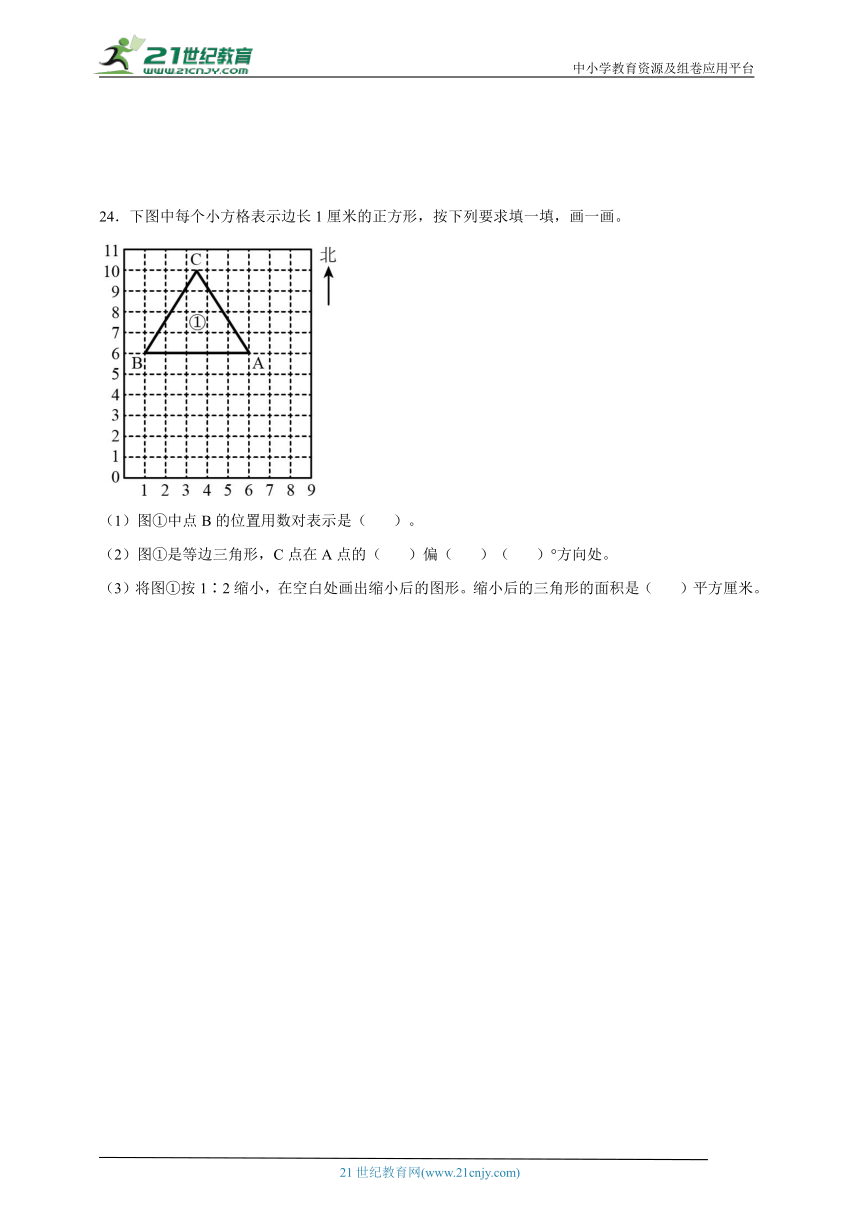
24.下图中每个小方格表示边长1厘米的正方形,按下列要求填一填,画一画。
(1)图①中点B的位置用数对表示是( )。
(2)图①是等边三角形,C点在A点的( )偏( )( )°方向处。
(3)将图①按1∶2缩小,在空白处画出缩小后的图形。缩小后的三角形的面积是( )平方厘米。
参考答案:
1.A
【分析】比例的基本性质:两内项之积等于两外项之积。据此分析解题。
【详解】A.5∶b=7∶a可得:5a=7b;
B.a∶b=5∶7可得:7a=5b;
C.b∶a=7∶5可得:7a=5b;
D.5∶a=7∶b可得:7a=5b;
所以,如果5a=7b,式子正确的是5∶b=7∶a。
故答案为:A
【点睛】本题考查了比例,掌握比例的基本性质是解题的关键。
2.C
【分析】两个相关联的量比值一定,那么这两个量成正比例关系,据此解题即可。
【详解】A.面积÷长=宽,长方形的宽一定,面积和长成正比例关系;
B.路程÷时间=速度,汽车的速度一定,总路程和时间成正比例关系;
C.被减数一定,减数和差不成比例;
D.除数=被除数÷商,除数一定,被除数和商成正比例关系。
故答案为:C
【点睛】考查正比例的判定,知道两个相关联的量比值一定,那么这两个量成正比例关系。
3.D
【分析】判断两个相关联的量之间成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例。
【详解】A.因为出勤人数+缺勤人数=全班人数(一定),则出勤人数和缺勤人数的和一定,所以出勤人数和缺勤人数不成比例;
B.因为每天运送的吨数×所需天数=货物总量(一定),每天运送的吨数和所需天数的乘积一定,则每天运送的吨数和所需天数成反比例;
C.因为单价×数量=总价(一定),单价和数量的乘积一定,则单价和数量成反比例;
D.因为水稻的总产量÷公顷数=水稻每公顷产量(一定),水稻的总产量与公顷数的比值一定,所以水稻的总产量与公顷数成正比例。
故答案为:D
【点睛】本题考查正反比例的判定,明确正反比例的定义是解题的关键。
4.C
【分析】设中央广播电视塔的实际总高度是x厘米,根据模型高度∶实际高度=1∶1000,列出比例解答即可。
【详解】解:设中央广播电视塔的实际总高度是x厘米。
40.5∶x=1∶1000
1x=40.5×1000
x=40500
40500厘米=405米
中央广播电视塔的实际总高度是405米。
故答案为:C
【点睛】用比例解决问题只要等号两边的比统一即可。
5.D
【分析】先统一单位,然后根据比例尺=图上距离∶实际距离,代入数据解答。
【详解】5毫米=0.5厘米
20厘米∶0.5厘米
=(20÷0.5)∶(0.5÷0.5)
=40∶1
一个零件长5毫米,在设计图纸上的长度是20厘米,图纸的比例尺是40∶1。
故答案为:D
【点睛】本题考查了比例尺的意义和求法,要注意统一单位。
6.D
【分析】先根据放大比例尺求出放大后的长方形的长和宽,再根据“长方形的面积=长×宽”求出放大后长方形的面积,据此解答。
【详解】长:10×3=30(cm)
宽:6×3=18(cm)
面积:30×18=540(cm2)
所以,得到的图形的面积是540cm2。
故答案为:D
【点睛】本题主要考查图形的放大与缩小,求出放大后长方形的长和宽是解答题目的关键。
7.5∶4=4.5∶3.6
【分析】比例的基本性质:在比例里,两个外项的积等于两个内项的积;据此解答。
【详解】根据4.5×4=3.6×5写出一个比例是5∶4=4.5∶3.6。
(答案不唯一)
【点睛】解答此题的关键是比例基本性质的逆运用,要注意:相乘的两个数要做外项就都做外项,要做内项就都做内项。
8. 正 反
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。
【详解】如果5=6,则=(一定),比值一定,那么和成正比例;
如果∶3=5∶,则=3×5=15(一定),乘积一定,那么和成反比例。
【点睛】掌握正、反比例的意义及辨识方法是解题的关键。
9.10
【分析】因为橡皮的弹性一定,所以原来B、C点的位置和拉长后B、C点的位置存在正比例关系,所以设此时点B的位置在xcm处,即可算出答案。
【详解】解:设此时点B的位置在xcm处。
6∶9=x∶15
9x=6×15
9x=90
9x÷9=90÷9
x=10
【点睛】此题考查了正比例关系以及解比例的应用。
10. 30 14
【分析】由线段比例尺可知,图上1厘米代表实际距离30千米,根据“比例尺=图上距离∶实际距离”求出数值比例尺,最后利用“图上距离=实际距离×比例尺”求出在这幅地图上的图上距离,据此解答。
【详解】图上1厘米表示实际距离30千米;
1厘米∶30千米
=1厘米∶3000000厘米
=1∶3000000
420千米=42000000厘米
42000000×=14(厘米)
即实际距离420千米在这幅地图上用14厘米表示。
【点睛】掌握比例尺的意义以及图上距离和实际距离换算的方法是解答题目的关键。
11. 1∶32/ 314
【分析】先统一单位,然后根据比例尺=图上距离∶实际距离,写出这张照片的比例尺;已知图纸上的比例尺是1∶500,根据实际距离=图上距离÷比例尺,用4÷即可求出4厘米的实际距离,再根据圆面积公式,代入数据解答即可。
【详解】1.6米=160厘米
5∶160
=(5÷5)∶(160÷5)
=1∶32
这张照片的比例尺是1∶32;
4÷
=4×500
=2000(厘米)
2000厘米=20米
3.14×(20÷2)2
=3.14×102
=3.14×100
=314(平方米)
这个草坪的实际面积是314平方米。
【点睛】本题主要考查了比例尺的意义、图上距离和实际距离的换算,圆面积公式的灵活应用,要熟练掌握相关公式。
12.24
【分析】先设原来卡片的单价是1,把原来卡片的单价看作单位“1”,现在每张卡片减价20%,则现在每张卡片的价格是原来的(1-20%),用原价乘(1-20%),求出现在每张卡片的价格;
根据“用同样多的钱”可知,总钱数不变,即单价×数量=总价(一定),乘积一定,则单价和数量成反比例关系,据此列出反比例方程,并求解。
【详解】设原来卡片的单价是1,现在卡片的单价是:
1×(1-20%)
=1×0.8
=0.8
解:设原来可以买张卡片。
1×=0.8×(+6)
=0.8+4.8
-0.8=4.8
0.2=4.8
=4.8÷0.2
=24
原来可以买24张卡片。
【点睛】先确定总钱数不变,再根据单价、数量、总价之间的关系,得出单价和数量成反比例关系,据此列出相应的比例方程。
13.√
【分析】根据比例的基本性质,把比例式化为乘积式,再结合倒数的定义可知,互为倒数的两个数的乘积是1,据此计算即可。
【详解】因为,所以xy==1,则和一定互为倒数。原题干说法正确。
故答案为:√
【点睛】本题考查比例的基本性质,结合倒数的定义是解题的关键。
14.×
【分析】比例尺=图上距离∶实际距离,据此求出比例尺即可判断。
【详解】20cm=200mm
这幅图的比例尺是200∶5=40∶1
所以原题说法错误。
故答案为:×
【点睛】熟练掌握比例尺的意义是解题的关键。
15.×
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫作成反比例的量,它们的关系叫作反比例关系,如果用字母和表示两种相关联的量,用表示它们的乘积(一定),反比例关系可以用表示,据此解答。
【详解】路程不一定时,汽车的速度和时间不成比例关系;路程一定时,速度×时间=路程(一定),此时汽车的速度和时间成反比例关系。
故答案为:×
【点睛】本题主要考查反比例关系的辨识,掌握反比例关系的意义是解答题目的关键。
16.×
【分析】根据比例的基本性质,把乘积式化为比例式即可。
【详解】因为a×3=b×5,所以a∶b=5∶3。原题干说法错误。
故答案为:×
【点睛】本题考查比例的基本性质,明确内项积等于外项积是解题的关键。
17.×
【分析】利用比例的基本性质,在比例里,两个外项的积等于两个内项的积。把a和看作比例的两个外项,把b和看作比例的两个内项,据此写出比例,求出a和b的比,即可比较得出a和b的大小。
【详解】若a×=b×
则a∶b=∶=(×12)∶(×12)=8∶9
所以可以看出a<b
故答案为:×
【点睛】此题主要通过比例的基本性质以及比的化简求解。
18.(1)不能组成比例;(2)可以组成比例,∶=∶1;
(3)可以组成比例,2.7∶1.8=6∶4;(4)不能组成比例。
【分析】根据比例的基本性质“两个外项的积等于两个内项的积”,分别计算出各组内项的积和外项的积,如果相等,就说明两个比能组成比例;如果不相等,就说明两个比不能组成比例。
【详解】(1)12×28=336
36×14=504
即:12×26≠36×14
所以,12∶36和14∶28,不能组成比例;
(2)×=
×1=
×=×1
所以,∶=∶1,即:∶和∶1可以组成比例。
(3)2.7×4=10.8
1.8×6=10.8
2.7×4=1.8×6
所以,2.7∶1.8=6∶4,即2.7∶1.8和6∶4可以组成比例。
(4)15×50=750
×4=
15×50≠×4
所以,15∶和4∶50,不能组成比例。
19.①;②;③
【分析】①先计算方程左边的,把方程化简成,然后方程两边同时除以,求出方程的解;
②先根据比例的基本性质把比例方程改写成,然后方程两边同时除以,求出方程的解;
③先根据比例的基本性质把比例方程改写成,然后方程两边同时除以,求出方程的解。
【详解】①
解:
②
解:
③
解:
20.7.5吨
【分析】根据题意知道总工作量一定,工作时间和工作效率成反比例,由此列式解答即可。
【详解】解:设每天应多生产x吨,可得:
40×(30+x)=30×50
1200+40x=1500
1200+40x-1200=1500-1200
40x=300
40x÷40=300÷40
x=7.5
答:每天应多生产7.5吨。
【点睛】解答此题的关键是,弄清题意,根据工作效率、工作时间和工作量之间的关系,先判断哪两种量成何比例,再找准对应量,列式解答即可。
21.6小时
【分析】首先计算A、B两地之间的实际距离,A、B两地之间的实际距离=图上距离÷比例尺;A、B两地之间的实际距离÷汽车的行驶速度=行驶时间,把数据代入即可求解。
【详解】8÷
=8×6000000
=48000000(厘米)
=480(千米)
480÷80=6(小时)
答:需要6小时到达。
【点睛】本题主要考查图上距离和实际距离的换算,同时熟练掌握行程问题的公式并灵活运用。
22.5千克
【分析】由“用药液和水按照1∶120配制而成”可以看出,农药的浓度一定,那么药液和水的质量的比值一定,所以药液和水的质量成正比例,设需要药液x千克,利用药液和水的比列出比例解答即可。
【详解】解:设需要药液x千克。
x∶(605-x)=1∶120
120x=605-x
120x+x=605-x+x
121x=605
121x÷121=605÷121
x=5
答:需要药液5千克。
【点睛】解答此题的关键是,先判断题中的两种相关联的量成何比例,然后找准对应量,列式解答即可。
23.(1)1∶10000;
(2)北偏东45°方向上;300;
(3)图见详解
【分析】(1)把线段比例尺改写成数值比例尺的方法:写出1厘米和1厘米所代表的实际距离的比,统一单位后再化成最简比的形式即可;
(2)根据地图上的方向“上北下南,左西右东”、“线段比例尺:图上1厘米表示实际距离100m”、及角度的信息;可知:邮局在学校的北偏东45°方向上,相距(100×3)m处。
(3)根据:“图上距离=实际距离×比例尺”,求出少年宫到学校的图上距离,再根据方向、角度等信息,标出少年宫的位置即可。
【详解】(1)根据题意可知,图上1个单位长度表示100米,可得:
1cm∶100m
=1cm∶10000cm
=1∶10000
所以,将这幅平面图的线段比例尺转化成数值比例尺是1∶10000;
(2)100×3=300(m)
邮局在学校的北偏东45°方向上,相距300m。
(3)250m=2500cm
2500×=2.5(cm)
少年宫的位置如下图:
【点睛】本题综合性较强,熟练掌握根据方向和距离确定位置以及比例尺的有关知识是关键。
24.(1)(1,6);(2)西;北;60 ;(3)见详解;2.5
【分析】(1)用数对表示位置时,前一个数表示第几列,后一个数表示第几行,据此表示出B点的位置;
(2)根据等边三角形的特征可知,∠CAB是60°,根据图上确定方向的方法:上北下南、左西右东,以A点为观测点,即可确定C点的方向;
(3)三角形按1∶2缩小,也就是把原来的底和高都缩小到原来的,已知原来的底和高分别是5厘米、4厘米,则分别用5÷2和4÷2即可求出缩小后的底和高,据此画图,再根据三角形的面积公式,求出缩小后的面积。
【详解】(1)图①中点B的位置用数对表示是(1,6);
(2)图①是等边三角形,C点在A点的西偏北60°方向处。
(3)原来的底和高分别是5厘米、4厘米,
5÷2=2.5(厘米)
4÷2=2(厘米)
2.5×2÷2=2.5(平方厘米)
缩小后的三角形的面积是2.5平方厘米。
如图②:
【点睛】本题主要考查了用数对表示位置、位置和方向、图形的缩小、三角形的面积,要熟练掌握每个知识点。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第4单元比例高频考点检测卷-数学六年级下册人教版
一、选择题
1.如果5a=7b,下列式子正确的是( )。
A.5∶b=7∶a B.a∶b=5∶7 C.b∶a=7∶5 D.5∶a=7∶b
2.以下哪个不成正比例( )。
A.长方形的宽一定,面积和长 B.汽车的速度一定,总路程和时间
C.被减数一定,减数和差 D.除数一定,被除数和商
3.下列各关系中,成正比例关系的是( )。
A.全班人数一定,出勤人数和缺勤人数 B.货物总量一定,每天运送的吨数和所需天数
C.总价一定,数量和单价 D.水稻每公顷产量一定,水稻的总产量与公顷数
4.如果按1∶1000的比例尺制作一个中央广播电视塔模型(包括避雷针),高为40.5cm。中央广播电视塔的实际总高度是( )米。
A.4.05 B.40.5 C.405 D.4050
5.一个零件长5毫米,在设计图纸上的长度是20厘米,图纸的比例尺是( )。
A.1∶4 B.4∶1 C.1∶40 D.40∶1
6.把一个长10cm、宽6cm的长方形按3∶1放大,得到的图形的面积是( )。
A. B. C. D.
二、填空题
7.根据4.5×4=3.6×5写出一个比例是( )。
8.如果5=6,那么和成( )比例;如果∶3=5∶,那么和成( )比例。
9.东东沿着直尺的方向将橡皮筋拉紧(如图,AC是橡皮筋示意图,B是橡皮筋上的一点)。如果点A的位置固定不变,沿着原来的方向将橡皮筋拉长,使点C的位置在15cm处,此时点B的位置在( )cm处。
10.在比例尺的地图上。1厘米表示实际距离( )千米,实际距离420千米,在这幅地图上用( )厘米表示。
11.小华身高1.6米,在照片上她的身高是5厘米,这张照片的比例尺是( );在一幅比例尺是1∶500的图纸上,量得一个圆形草坪的直径是4厘米,这个草坪的实际面积是( )平方米。
12.为了庆祝六一节每张卡片减价20%,用同样多的钱可以多买6张,原来可以买( )张卡片。
三、判断题
13.如果,那么和一定互为倒数。( )
14.一个5mm长零件画在图纸上的长是20cm,这幅图的比例尺是1∶40。( )
15.汽车的速度和时间成反比例关系。( )
16.如果a×3=b×5(a、b均不为0),那么a∶b=3∶5。( )
17.a和b都不为0,a×=b×,那么a>b。( )
四、计算题
18.应用比例的基本性质,判断下面哪几组的两个比可以组成比例。把组成的比例写出来。
(1)和 (2)和
(3)和 (4)和
19.解方程或比例。
① ② ③
五、解答题
20.化肥厂生产一批化肥,每天生产30吨,50天完成。如果要40天完成任务,每天应多生产多少吨?(用比例解)
21.在比例尺为1∶6000000的地图上量得A、B两地相距8厘米,一辆货车以每小时80千米的速度从A地开往B地。需要多少小时到达?
22.一种稀释消毒液,用药液和水按1∶120配制而成。要配制这种稀释消毒液605千克,需要药液多少千克?(用比例知识解答)
23.按要求完成下列各题。
(1)将这幅平面图的线段比例尺转化成数值比例尺是( )。
(2)邮局在学校的( ),相距( )m。
(3)少年宫在学校的西偏北30°方向上250m处,请按给定的比例尺画出少年宫的位置。
24.下图中每个小方格表示边长1厘米的正方形,按下列要求填一填,画一画。
(1)图①中点B的位置用数对表示是( )。
(2)图①是等边三角形,C点在A点的( )偏( )( )°方向处。
(3)将图①按1∶2缩小,在空白处画出缩小后的图形。缩小后的三角形的面积是( )平方厘米。
参考答案:
1.A
【分析】比例的基本性质:两内项之积等于两外项之积。据此分析解题。
【详解】A.5∶b=7∶a可得:5a=7b;
B.a∶b=5∶7可得:7a=5b;
C.b∶a=7∶5可得:7a=5b;
D.5∶a=7∶b可得:7a=5b;
所以,如果5a=7b,式子正确的是5∶b=7∶a。
故答案为:A
【点睛】本题考查了比例,掌握比例的基本性质是解题的关键。
2.C
【分析】两个相关联的量比值一定,那么这两个量成正比例关系,据此解题即可。
【详解】A.面积÷长=宽,长方形的宽一定,面积和长成正比例关系;
B.路程÷时间=速度,汽车的速度一定,总路程和时间成正比例关系;
C.被减数一定,减数和差不成比例;
D.除数=被除数÷商,除数一定,被除数和商成正比例关系。
故答案为:C
【点睛】考查正比例的判定,知道两个相关联的量比值一定,那么这两个量成正比例关系。
3.D
【分析】判断两个相关联的量之间成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例。
【详解】A.因为出勤人数+缺勤人数=全班人数(一定),则出勤人数和缺勤人数的和一定,所以出勤人数和缺勤人数不成比例;
B.因为每天运送的吨数×所需天数=货物总量(一定),每天运送的吨数和所需天数的乘积一定,则每天运送的吨数和所需天数成反比例;
C.因为单价×数量=总价(一定),单价和数量的乘积一定,则单价和数量成反比例;
D.因为水稻的总产量÷公顷数=水稻每公顷产量(一定),水稻的总产量与公顷数的比值一定,所以水稻的总产量与公顷数成正比例。
故答案为:D
【点睛】本题考查正反比例的判定,明确正反比例的定义是解题的关键。
4.C
【分析】设中央广播电视塔的实际总高度是x厘米,根据模型高度∶实际高度=1∶1000,列出比例解答即可。
【详解】解:设中央广播电视塔的实际总高度是x厘米。
40.5∶x=1∶1000
1x=40.5×1000
x=40500
40500厘米=405米
中央广播电视塔的实际总高度是405米。
故答案为:C
【点睛】用比例解决问题只要等号两边的比统一即可。
5.D
【分析】先统一单位,然后根据比例尺=图上距离∶实际距离,代入数据解答。
【详解】5毫米=0.5厘米
20厘米∶0.5厘米
=(20÷0.5)∶(0.5÷0.5)
=40∶1
一个零件长5毫米,在设计图纸上的长度是20厘米,图纸的比例尺是40∶1。
故答案为:D
【点睛】本题考查了比例尺的意义和求法,要注意统一单位。
6.D
【分析】先根据放大比例尺求出放大后的长方形的长和宽,再根据“长方形的面积=长×宽”求出放大后长方形的面积,据此解答。
【详解】长:10×3=30(cm)
宽:6×3=18(cm)
面积:30×18=540(cm2)
所以,得到的图形的面积是540cm2。
故答案为:D
【点睛】本题主要考查图形的放大与缩小,求出放大后长方形的长和宽是解答题目的关键。
7.5∶4=4.5∶3.6
【分析】比例的基本性质:在比例里,两个外项的积等于两个内项的积;据此解答。
【详解】根据4.5×4=3.6×5写出一个比例是5∶4=4.5∶3.6。
(答案不唯一)
【点睛】解答此题的关键是比例基本性质的逆运用,要注意:相乘的两个数要做外项就都做外项,要做内项就都做内项。
8. 正 反
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。
【详解】如果5=6,则=(一定),比值一定,那么和成正比例;
如果∶3=5∶,则=3×5=15(一定),乘积一定,那么和成反比例。
【点睛】掌握正、反比例的意义及辨识方法是解题的关键。
9.10
【分析】因为橡皮的弹性一定,所以原来B、C点的位置和拉长后B、C点的位置存在正比例关系,所以设此时点B的位置在xcm处,即可算出答案。
【详解】解:设此时点B的位置在xcm处。
6∶9=x∶15
9x=6×15
9x=90
9x÷9=90÷9
x=10
【点睛】此题考查了正比例关系以及解比例的应用。
10. 30 14
【分析】由线段比例尺可知,图上1厘米代表实际距离30千米,根据“比例尺=图上距离∶实际距离”求出数值比例尺,最后利用“图上距离=实际距离×比例尺”求出在这幅地图上的图上距离,据此解答。
【详解】图上1厘米表示实际距离30千米;
1厘米∶30千米
=1厘米∶3000000厘米
=1∶3000000
420千米=42000000厘米
42000000×=14(厘米)
即实际距离420千米在这幅地图上用14厘米表示。
【点睛】掌握比例尺的意义以及图上距离和实际距离换算的方法是解答题目的关键。
11. 1∶32/ 314
【分析】先统一单位,然后根据比例尺=图上距离∶实际距离,写出这张照片的比例尺;已知图纸上的比例尺是1∶500,根据实际距离=图上距离÷比例尺,用4÷即可求出4厘米的实际距离,再根据圆面积公式,代入数据解答即可。
【详解】1.6米=160厘米
5∶160
=(5÷5)∶(160÷5)
=1∶32
这张照片的比例尺是1∶32;
4÷
=4×500
=2000(厘米)
2000厘米=20米
3.14×(20÷2)2
=3.14×102
=3.14×100
=314(平方米)
这个草坪的实际面积是314平方米。
【点睛】本题主要考查了比例尺的意义、图上距离和实际距离的换算,圆面积公式的灵活应用,要熟练掌握相关公式。
12.24
【分析】先设原来卡片的单价是1,把原来卡片的单价看作单位“1”,现在每张卡片减价20%,则现在每张卡片的价格是原来的(1-20%),用原价乘(1-20%),求出现在每张卡片的价格;
根据“用同样多的钱”可知,总钱数不变,即单价×数量=总价(一定),乘积一定,则单价和数量成反比例关系,据此列出反比例方程,并求解。
【详解】设原来卡片的单价是1,现在卡片的单价是:
1×(1-20%)
=1×0.8
=0.8
解:设原来可以买张卡片。
1×=0.8×(+6)
=0.8+4.8
-0.8=4.8
0.2=4.8
=4.8÷0.2
=24
原来可以买24张卡片。
【点睛】先确定总钱数不变,再根据单价、数量、总价之间的关系,得出单价和数量成反比例关系,据此列出相应的比例方程。
13.√
【分析】根据比例的基本性质,把比例式化为乘积式,再结合倒数的定义可知,互为倒数的两个数的乘积是1,据此计算即可。
【详解】因为,所以xy==1,则和一定互为倒数。原题干说法正确。
故答案为:√
【点睛】本题考查比例的基本性质,结合倒数的定义是解题的关键。
14.×
【分析】比例尺=图上距离∶实际距离,据此求出比例尺即可判断。
【详解】20cm=200mm
这幅图的比例尺是200∶5=40∶1
所以原题说法错误。
故答案为:×
【点睛】熟练掌握比例尺的意义是解题的关键。
15.×
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫作成反比例的量,它们的关系叫作反比例关系,如果用字母和表示两种相关联的量,用表示它们的乘积(一定),反比例关系可以用表示,据此解答。
【详解】路程不一定时,汽车的速度和时间不成比例关系;路程一定时,速度×时间=路程(一定),此时汽车的速度和时间成反比例关系。
故答案为:×
【点睛】本题主要考查反比例关系的辨识,掌握反比例关系的意义是解答题目的关键。
16.×
【分析】根据比例的基本性质,把乘积式化为比例式即可。
【详解】因为a×3=b×5,所以a∶b=5∶3。原题干说法错误。
故答案为:×
【点睛】本题考查比例的基本性质,明确内项积等于外项积是解题的关键。
17.×
【分析】利用比例的基本性质,在比例里,两个外项的积等于两个内项的积。把a和看作比例的两个外项,把b和看作比例的两个内项,据此写出比例,求出a和b的比,即可比较得出a和b的大小。
【详解】若a×=b×
则a∶b=∶=(×12)∶(×12)=8∶9
所以可以看出a<b
故答案为:×
【点睛】此题主要通过比例的基本性质以及比的化简求解。
18.(1)不能组成比例;(2)可以组成比例,∶=∶1;
(3)可以组成比例,2.7∶1.8=6∶4;(4)不能组成比例。
【分析】根据比例的基本性质“两个外项的积等于两个内项的积”,分别计算出各组内项的积和外项的积,如果相等,就说明两个比能组成比例;如果不相等,就说明两个比不能组成比例。
【详解】(1)12×28=336
36×14=504
即:12×26≠36×14
所以,12∶36和14∶28,不能组成比例;
(2)×=
×1=
×=×1
所以,∶=∶1,即:∶和∶1可以组成比例。
(3)2.7×4=10.8
1.8×6=10.8
2.7×4=1.8×6
所以,2.7∶1.8=6∶4,即2.7∶1.8和6∶4可以组成比例。
(4)15×50=750
×4=
15×50≠×4
所以,15∶和4∶50,不能组成比例。
19.①;②;③
【分析】①先计算方程左边的,把方程化简成,然后方程两边同时除以,求出方程的解;
②先根据比例的基本性质把比例方程改写成,然后方程两边同时除以,求出方程的解;
③先根据比例的基本性质把比例方程改写成,然后方程两边同时除以,求出方程的解。
【详解】①
解:
②
解:
③
解:
20.7.5吨
【分析】根据题意知道总工作量一定,工作时间和工作效率成反比例,由此列式解答即可。
【详解】解:设每天应多生产x吨,可得:
40×(30+x)=30×50
1200+40x=1500
1200+40x-1200=1500-1200
40x=300
40x÷40=300÷40
x=7.5
答:每天应多生产7.5吨。
【点睛】解答此题的关键是,弄清题意,根据工作效率、工作时间和工作量之间的关系,先判断哪两种量成何比例,再找准对应量,列式解答即可。
21.6小时
【分析】首先计算A、B两地之间的实际距离,A、B两地之间的实际距离=图上距离÷比例尺;A、B两地之间的实际距离÷汽车的行驶速度=行驶时间,把数据代入即可求解。
【详解】8÷
=8×6000000
=48000000(厘米)
=480(千米)
480÷80=6(小时)
答:需要6小时到达。
【点睛】本题主要考查图上距离和实际距离的换算,同时熟练掌握行程问题的公式并灵活运用。
22.5千克
【分析】由“用药液和水按照1∶120配制而成”可以看出,农药的浓度一定,那么药液和水的质量的比值一定,所以药液和水的质量成正比例,设需要药液x千克,利用药液和水的比列出比例解答即可。
【详解】解:设需要药液x千克。
x∶(605-x)=1∶120
120x=605-x
120x+x=605-x+x
121x=605
121x÷121=605÷121
x=5
答:需要药液5千克。
【点睛】解答此题的关键是,先判断题中的两种相关联的量成何比例,然后找准对应量,列式解答即可。
23.(1)1∶10000;
(2)北偏东45°方向上;300;
(3)图见详解
【分析】(1)把线段比例尺改写成数值比例尺的方法:写出1厘米和1厘米所代表的实际距离的比,统一单位后再化成最简比的形式即可;
(2)根据地图上的方向“上北下南,左西右东”、“线段比例尺:图上1厘米表示实际距离100m”、及角度的信息;可知:邮局在学校的北偏东45°方向上,相距(100×3)m处。
(3)根据:“图上距离=实际距离×比例尺”,求出少年宫到学校的图上距离,再根据方向、角度等信息,标出少年宫的位置即可。
【详解】(1)根据题意可知,图上1个单位长度表示100米,可得:
1cm∶100m
=1cm∶10000cm
=1∶10000
所以,将这幅平面图的线段比例尺转化成数值比例尺是1∶10000;
(2)100×3=300(m)
邮局在学校的北偏东45°方向上,相距300m。
(3)250m=2500cm
2500×=2.5(cm)
少年宫的位置如下图:
【点睛】本题综合性较强,熟练掌握根据方向和距离确定位置以及比例尺的有关知识是关键。
24.(1)(1,6);(2)西;北;60 ;(3)见详解;2.5
【分析】(1)用数对表示位置时,前一个数表示第几列,后一个数表示第几行,据此表示出B点的位置;
(2)根据等边三角形的特征可知,∠CAB是60°,根据图上确定方向的方法:上北下南、左西右东,以A点为观测点,即可确定C点的方向;
(3)三角形按1∶2缩小,也就是把原来的底和高都缩小到原来的,已知原来的底和高分别是5厘米、4厘米,则分别用5÷2和4÷2即可求出缩小后的底和高,据此画图,再根据三角形的面积公式,求出缩小后的面积。
【详解】(1)图①中点B的位置用数对表示是(1,6);
(2)图①是等边三角形,C点在A点的西偏北60°方向处。
(3)原来的底和高分别是5厘米、4厘米,
5÷2=2.5(厘米)
4÷2=2(厘米)
2.5×2÷2=2.5(平方厘米)
缩小后的三角形的面积是2.5平方厘米。
如图②:
【点睛】本题主要考查了用数对表示位置、位置和方向、图形的缩小、三角形的面积,要熟练掌握每个知识点。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
