集合(江苏省徐州市)

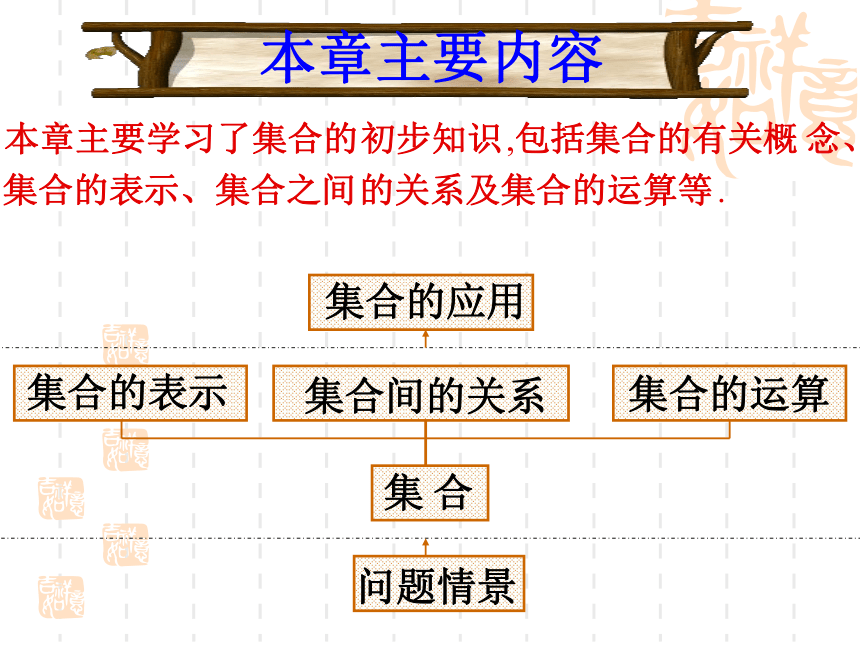
课件14张PPT。第一章:集 合本章主要内容⑴集合的基本性质、元素与集合的关系、集合的表示方法；
⑵子集、真子集、补集的概念；
⑶集合的交、并、补运算；
⑷集合问题的解答方法：Venn图示法、数轴分析法.知识要点数学应用集合的三个特征、元素与集合的关系元素的确定性；
元素的互异性；
元素的无序性；例１、求集合{1，x2－x－1}中实数x应满足的条件．例2、 集合A＝{x | x2－2ax＋b＝0 x∈R}，
（1）若A＝{－1，1}，求a、b．
（2）若A＝{－1}，求a、b．例3、已知集合M={-2，3x2+3x-4,x2+x-4},若2∈M，
求x的值.数学应用例5、用另一种方法表示集合：集 合的表示方法
数学应用子集、真子集的问题
例6、已知集合A＝{1，3，a}，Ｂ＝{1，a2－a＋ 1}
若B?A，求a的值.
解：因为B?A，故有a2－a＋1＝3或a2－a＋1＝a.
1. 由a2－a＋1＝3解得a＝2或a＝－1.经检验，它
们均满足题设条件.
2.由a2－a＋1＝a解得，a＝1.此时集合A中有两个
元素1，与元素的互异性相矛盾，故知a＝1不合题
意，应舍去.综上所述，所求a的值是－1或2.数学应用子集、真子集的问题
例7、 已知集合A＝{x|x2＋ax＋1＝0}，B＝{1,2}，且
A?B，求a的取值范围.
解:∵A是B的子集，故知集合A可能为　?，{1}，{2}，{1,2}.由根与系数的关系可知x1·x2＝1，知A＝{2}及A＝{1,2}均不可能．因而A＝?或{1}．
当A＝?时，即方程x2＋ax＋1＝0没有实数解，故知
a2－4<0，即－2当A＝{1}时，即方程有两个相等的根1，由根与系数的关系可知，1＋1＝－a，即a＝－2.
综上所述，所求a的范围是－2≤a<2.数学应用集合的交、并、补运算
例8、设二次方程 x2＋ax＋b＝0和x2＋cx＋15＝0的解集分别为A、B，又A∪B＝{3，5}， A∩B＝{3}，求a， b， c的值．
解 ∵ A∩B＝{3},
∴ 3∈B，即3是方程x2＋cx＋15＝0的根.
∴ 32＋3c＋15＝0 得 c＝－8.
由方程x2－8x＋15＝0 解得 x1＝3， x2＝5,
∴ B＝{3， 5}.又A∪B＝{3，5}，故必有A＝{3}，即方程x2＋ax＋b＝0有
两重根为3,由韦达定理可得 a＝－6， b＝9.
例 9 、已知全集U＝{1，2，3，4，5}，A＝{x|x2
－5x＋q＝0}，求?UA及q的值.
分析:由U是全集，可知A ? U.但A是表示方程的
解集，故A中最多只能有两个元素.
又方程x2－5x＋q＝0的根必是U中的元素.结合根与
系数的关系可知，A中有一个元素的情况不可能.
故A＝?或A中必有两不等实根，且两元素之和为5.
所以A的可能情况为A＝?、A＝{ 1，4}、A＝{2，
3}.（1）当A＝?时，?UA＝U，此时，25－4q＜0，知q＞25/4，即q的值为大于25/4的实数；
（2）当A＝{1，4}时，?UA＝{2，3，5}，此时
q＝1·4＝4；（3）当A＝{2，3}时，?UA＝{1，4，5}，此时q＝2·3＝6.数学应用Venn图示法、数轴分析法
例10、分别用集合A,B,C表示下图的阴影部分例11、已知集合A=}121|{-￡￡+=mxmxB课堂练习
教材第13页 习题7、8.回顾反思
本节课我们学习复习了集合这一章，并处理了一些与集合有关的问题.我们在处理有关集合问题时一定要注意集合的性质.
教材第17页 习题1—9.课后作业再见