2024版《课时节节练》数学选择性必修第一册RJ A第一章 1.4 空间向量的应用 1.4.1 用空间向量研究直线、平面的位置关系12
文档属性
| 名称 | 2024版《课时节节练》数学选择性必修第一册RJ A第一章 1.4 空间向量的应用 1.4.1 用空间向量研究直线、平面的位置关系12 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-07 13:07:27 | ||
图片预览

文档简介
第一章 空间向量与立体几何
课时把关练
1.4 空间向量的应用
1.4.1 用空间向量研究直线、平面的位置关系
1.已知平面内有一点M(1,-1,2),平面的一个法向量为=(6,-3,6),则下列点P中,在平面内的是( )
A.P(2,3,3) B.P(-2,0,1) C.P(-4,4,0) D.P(3,-3,4)
2.如果直线l的方向向量是,且直线l上有一点P不在平面α内,平面α的法向量是,那么( )
A. B. C. D.l与α斜交
3.(多选题)已知,是坐标原点,则下列各向量中是平面的法向量的是( )
A. B. C. D.
4.(多选题)设直线l的方向向量为,平面的法向量为, l?,则使l∥成立的有( )
A. , B. ,
C. , D. ,
5.如图,正方形与矩形所在平面互相垂直,,,
M在上,且平面.则M点的坐标为( )
A. B. C. D.
6.(多选题)如图,在正方体ABCD-A1B1C1D1中,点E,F是BC上的两个三等分点,点G,H是A1D1上的两个三等分点,点M,N,P分别为AB,C1D1和CD的中点,
点Q是A1M上的一个动点,下面结论中正确的是( )
A. FH与AC1异面且垂直 B. FG与AC1相交且垂直
C. D1Q∥平面EFN D. B1,H,F,P四点共面
7.(多选题)下列四个正方体图形中,l是正方体的一条体对角线,点M,N,P
分别为其所在棱的中点,能得出l⊥平面MNP的是( )
A B C D
8.已知平面α经过点,且是α的一个法向量,是平面α内任意一点,则x,y,z满足的关系式是________________.
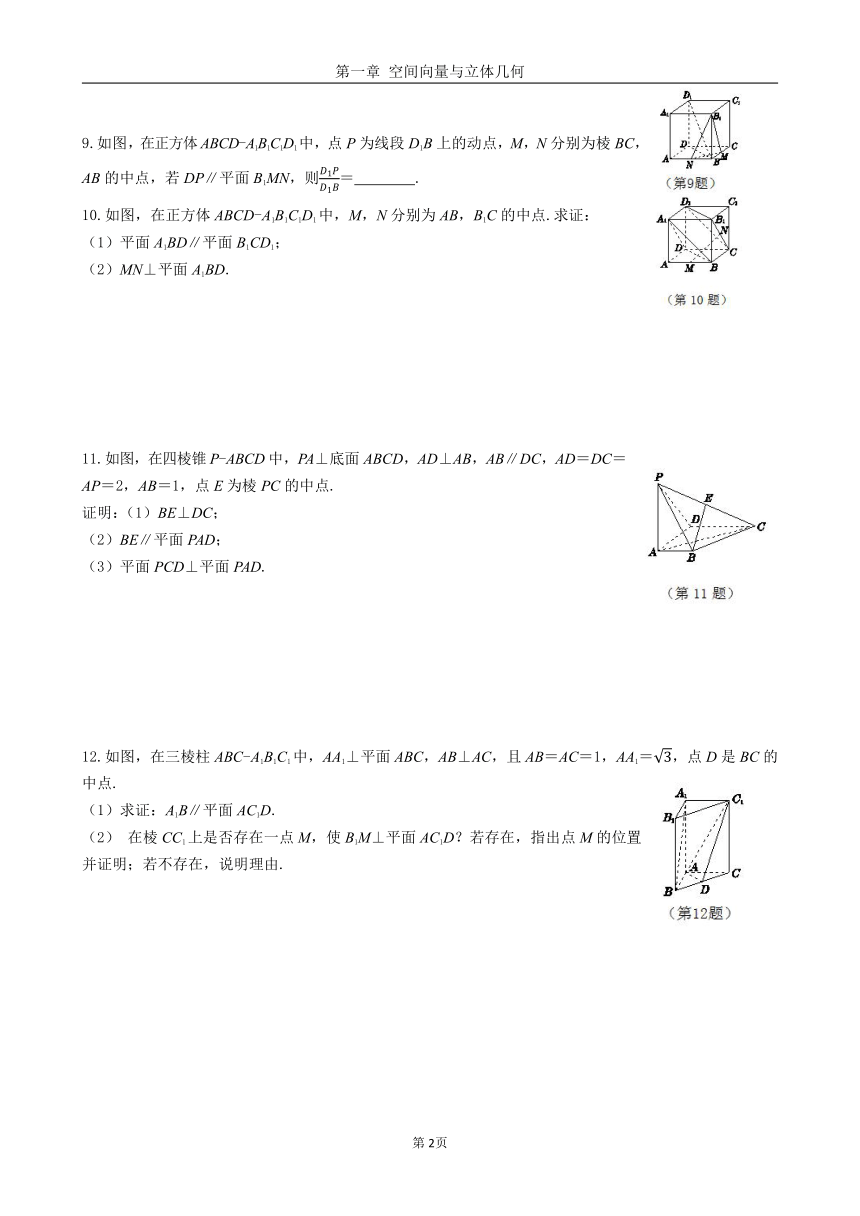
9.如图,在正方体ABCD-A1B1C1D1中,点P为线段D1B上的动点,M,N分别为棱BC,AB的中点,若DP∥平面B1MN,则= .
10.如图,在正方体ABCD-A1B1C1D1中,M,N分别为AB,B1C的中点.求证:
(1)平面A1BD∥平面B1CD1;
(2)MN⊥平面A1BD.
11.如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
证明:(1)BE⊥DC;
(2)BE∥平面PAD;
(3)平面PCD⊥平面PAD.
12.如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,且AB=AC=1,AA1=,点D是BC的中点.
(1)求证:A1B∥平面AC1D.
(2) 在棱CC1上是否存在一点M,使B1M⊥平面AC1D?若存在,指出点M的位置并证明;若不存在,说明理由.
课时把关练
1.4 空间向量的应用
1.4.1 用空间向量研究直线、平面的位置关系
参考答案
1.A 2.B 3.BD 4.BD 5.C 6.ACD 7.ACD 8. 9.
10. 证明:(1)建立如图所示的空间直角坐标系Dxyz,设正方体的棱长为2,则D(0,0,0),A1(2,0,2),B(2,2,0),B1(2,2,2),C(0,2,0),D1(0,0,2).
设平面A1BD的法向量为=(x,y,z),
∵=(2,0,2),=(2,2,0),
且∴
取x=-1,得y=1,z=1,∴ =(-1,1,1).
同理可求得平面B1CD1的一个法向量为n=(-1,1,1).
∵ ∴ ∥,
∴ 平面A1BD∥平面B1CD1.
(2)∵ M,N分别为AB,B1C的中点,∴ M(2,1,0),N(1,2,1),
∴=(-1,1,1),∴∥,
∴ MN⊥平面A1BD.
11. 证明:以点A为坐标原点,AB,AD,AP所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系.可得B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2),
由E为PC的中点,得E(1,1,1).
(1)向量=(0,1,1),=(2,0,0),故·=0,
∴ BE⊥DC.
(2)∵ PA⊥平面ABCD,AB?平面ABCD,∴ AB⊥PA.
∵ AB⊥AD,PA∩AD=A,
∴ AB⊥平面PAD.
∴ 向量=(1,0,0)为平面PAD的一个法向量.
而·=0,∴⊥.
又∵ BE?平面PAD,∴ BE∥平面PAD.
(3)由(2)知平面PAD的一个法向量为=(1,0,0),
向量=(0,2,-2),=(2,0,0),
设平面PCD的一个法向量为=(x,y,z),
则
取y=1,可得平面PCD的一个法向量为=(0,1,1).
∵·,∴ ⊥,
∴ 平面PCD⊥平面PAD.
12. (1)证明:以A为坐标原点,以AB,AC,AA1所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系Axyz,则A(0,0,0),B(1,0,0),C(0,1,0),A1(0,0,),C1(0,1,),
,B1(1,0,).
所以=(1,0,-),=,=(0,1,).
设平面AC1D的一个法向量为=(x,y,z),
则有取z=1,则x=,y=-.
所以=(,-,1).
所以·=1×+0× (-)+(-)×1=0,所以⊥.
因为A1B?平面AC1D,所以A1B∥平面AC1D.
(2)解:存在.假设在棱CC1上存在一点M,使B1M⊥平面AC1D.
设M(0,1,λ),λ∈[0,],则=(-1,1,λ-).
由(1)知,平面AC1D的一个法向量为=(,-,1),若B1M⊥平面AC1D,则∥.
所以==,解得λ=∈[0,],即M,且=.
所以在棱CC1上存在一点M,且满足=,使B1M⊥平面AC1D.
第4页
课时把关练
1.4 空间向量的应用
1.4.1 用空间向量研究直线、平面的位置关系
1.已知平面内有一点M(1,-1,2),平面的一个法向量为=(6,-3,6),则下列点P中,在平面内的是( )
A.P(2,3,3) B.P(-2,0,1) C.P(-4,4,0) D.P(3,-3,4)
2.如果直线l的方向向量是,且直线l上有一点P不在平面α内,平面α的法向量是,那么( )
A. B. C. D.l与α斜交
3.(多选题)已知,是坐标原点,则下列各向量中是平面的法向量的是( )
A. B. C. D.
4.(多选题)设直线l的方向向量为,平面的法向量为, l?,则使l∥成立的有( )
A. , B. ,
C. , D. ,
5.如图,正方形与矩形所在平面互相垂直,,,
M在上,且平面.则M点的坐标为( )
A. B. C. D.
6.(多选题)如图,在正方体ABCD-A1B1C1D1中,点E,F是BC上的两个三等分点,点G,H是A1D1上的两个三等分点,点M,N,P分别为AB,C1D1和CD的中点,
点Q是A1M上的一个动点,下面结论中正确的是( )
A. FH与AC1异面且垂直 B. FG与AC1相交且垂直
C. D1Q∥平面EFN D. B1,H,F,P四点共面
7.(多选题)下列四个正方体图形中,l是正方体的一条体对角线,点M,N,P
分别为其所在棱的中点,能得出l⊥平面MNP的是( )
A B C D
8.已知平面α经过点,且是α的一个法向量,是平面α内任意一点,则x,y,z满足的关系式是________________.
9.如图,在正方体ABCD-A1B1C1D1中,点P为线段D1B上的动点,M,N分别为棱BC,AB的中点,若DP∥平面B1MN,则= .
10.如图,在正方体ABCD-A1B1C1D1中,M,N分别为AB,B1C的中点.求证:
(1)平面A1BD∥平面B1CD1;
(2)MN⊥平面A1BD.
11.如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
证明:(1)BE⊥DC;
(2)BE∥平面PAD;
(3)平面PCD⊥平面PAD.
12.如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,且AB=AC=1,AA1=,点D是BC的中点.
(1)求证:A1B∥平面AC1D.
(2) 在棱CC1上是否存在一点M,使B1M⊥平面AC1D?若存在,指出点M的位置并证明;若不存在,说明理由.
课时把关练
1.4 空间向量的应用
1.4.1 用空间向量研究直线、平面的位置关系
参考答案
1.A 2.B 3.BD 4.BD 5.C 6.ACD 7.ACD 8. 9.
10. 证明:(1)建立如图所示的空间直角坐标系Dxyz,设正方体的棱长为2,则D(0,0,0),A1(2,0,2),B(2,2,0),B1(2,2,2),C(0,2,0),D1(0,0,2).
设平面A1BD的法向量为=(x,y,z),
∵=(2,0,2),=(2,2,0),
且∴
取x=-1,得y=1,z=1,∴ =(-1,1,1).
同理可求得平面B1CD1的一个法向量为n=(-1,1,1).
∵ ∴ ∥,
∴ 平面A1BD∥平面B1CD1.
(2)∵ M,N分别为AB,B1C的中点,∴ M(2,1,0),N(1,2,1),
∴=(-1,1,1),∴∥,
∴ MN⊥平面A1BD.
11. 证明:以点A为坐标原点,AB,AD,AP所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系.可得B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2),
由E为PC的中点,得E(1,1,1).
(1)向量=(0,1,1),=(2,0,0),故·=0,
∴ BE⊥DC.
(2)∵ PA⊥平面ABCD,AB?平面ABCD,∴ AB⊥PA.
∵ AB⊥AD,PA∩AD=A,
∴ AB⊥平面PAD.
∴ 向量=(1,0,0)为平面PAD的一个法向量.
而·=0,∴⊥.
又∵ BE?平面PAD,∴ BE∥平面PAD.
(3)由(2)知平面PAD的一个法向量为=(1,0,0),
向量=(0,2,-2),=(2,0,0),
设平面PCD的一个法向量为=(x,y,z),
则
取y=1,可得平面PCD的一个法向量为=(0,1,1).
∵·,∴ ⊥,
∴ 平面PCD⊥平面PAD.
12. (1)证明:以A为坐标原点,以AB,AC,AA1所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系Axyz,则A(0,0,0),B(1,0,0),C(0,1,0),A1(0,0,),C1(0,1,),
,B1(1,0,).
所以=(1,0,-),=,=(0,1,).
设平面AC1D的一个法向量为=(x,y,z),
则有取z=1,则x=,y=-.
所以=(,-,1).
所以·=1×+0× (-)+(-)×1=0,所以⊥.
因为A1B?平面AC1D,所以A1B∥平面AC1D.
(2)解:存在.假设在棱CC1上存在一点M,使B1M⊥平面AC1D.
设M(0,1,λ),λ∈[0,],则=(-1,1,λ-).
由(1)知,平面AC1D的一个法向量为=(,-,1),若B1M⊥平面AC1D,则∥.
所以==,解得λ=∈[0,],即M,且=.
所以在棱CC1上存在一点M,且满足=,使B1M⊥平面AC1D.
第4页
