【五环分层导学-课件】2-18 单元复习 有理数及其运算-北师大版数学七(上)
文档属性
| 名称 | 【五环分层导学-课件】2-18 单元复习 有理数及其运算-北师大版数学七(上) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-02 00:00:00 | ||
图片预览











文档简介
(共40张PPT)
第二章 有理数及其运算
单元复习
北师大版七年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
资料简介
【问题1】请你构思一个生活中的场景,使其尽可能多地包含负数、数轴、绝对值?
【问题2】举例说明你是怎样获得有理数加法或减法的运算法则的运算内容?
【问题3】有理数有哪些运算法则和运算律?
【问题4】有理数的运算与小学学过的有关数的运算有什么联系?你能举例说明吗?
【问题5】生活中你遇到过用科学记数法表示的“大数”吗?你能举例说明吗?
【问题6】梳理本章内容,用适当的方式(可以用表格、思维导图、列要点)呈现全章知识结构.
【例题1】《九章算术》中有注:“今两算得失相反,要令正负以名之.”意思是:“今有两数若其意义相反,则分别叫做正数和负数.”如果水位升高5米记为+5米,那么水位下降3米应记为(%////%)
A.-5米 B.+5米 C.-2米 D.-3米
D
【例题2】将下列各数填入相应的大括号里.
-,0.618,-3.14,260,-2,,-0.010010001…(每相邻两个1之间依次多一个0),0,.
正数集合:{%// //% };
负数集合:{%// };
整数集合:{%// //% };
分数集合:{%// //% };
0.618,260,,
,-3.14,-2,-0.010010001…
260,-2,0
,0.618,-3.14,,
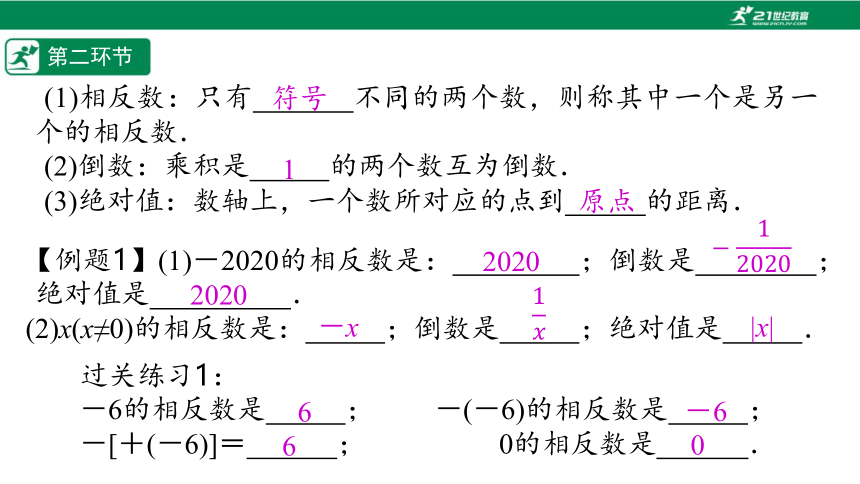
(1)相反数:只有%/// /%不同的两个数,则称其中一个是另一个的相反数.
(2)倒数:乘积是%////%的两个数互为倒数.
(3)绝对值:数轴上,一个数所对应的点到%// //%的距离.
【例题1】(1)-2020的相反数是:%// / /%;倒数是%// //%;绝对值是%// //%.
(2)x(x≠0)的相反数是:%////%;倒数是%////%;绝对值是%////%.
2020
2020
-x
|x|
符号
1
原点
过关练习1:
-6的相反数是%////%; -(-6)的相反数是%////%;
-[+(-6)]=%/// /%; 0的相反数是%//// %.
6
-6
6
0
过关练习2:
(1)a的倒数是%////%(a≠0);
(2)若a与b互为倒数,则%// //%;倒数是它本身的是%// //%.
(3)-的相反数的倒数是%////%.
ab=1
1和-1
6
过关练习3:
(1)-4的绝对值表示它离开原点的距离是%////个单位,记作// %.
(2)|-6|=%////%;-|-6|=%////%;绝对值等于6的数是%////%.
(3)绝对值等于其相反数的数是%// //%.
(4)绝对值不大于11的整数有
% // //%.
4
|-4|
6
-6
±6
负数或0
0,±1,±2,±3,±4,±5,±6,±7,±8,±9,±10
规定了%// //%、%// //%和%// //%的一条%// //%.
原点
正方向
单位长度
直线
【例题1】把下列各数表示在如图所示数轴上,然后把这些数按从大到小的顺序用“>”连接起来.
0,1,-3,-(-0.5),-|-|,+(-4).
根据数轴的特点把这些数按从大到小的顺序用“>”连接起来为:
1>(-0.5)>0>-||>-3>+(-4).
【例题2】实数a,b在数轴上的对应点的位置如图所示,则正确的结论是(%////%)
A.a>-2 B.a<-3 C.a>-b D.a<-b
D
过关练习1:如图,数轴的单位长度为1,如果点A表示的数是-3,那么点B表示的数是(%////%)
A.0 B.1 C.2 D.3
过关练习2:点A,B在数轴上的位置如图所示,如果点C也在数轴上,且B和C两点间的距离是1,那么AC长度为%// //%.
B
2或4
【例题1】下列各数中,最小的数是(%////%)
A.-3 B.|-2| C.(-3)2 D.2×10-5
A
【例题2】比较大小:%////%-0.009; -%////%-.
>
<
(1)有理数的加法
①(+5)+(+8)=%// //%; ②(-5)+(-8)=%// //%;
③(+12)+(-10)=%// //%; ④2+3=%// //%;
⑤(-2)+(-3)=%// //%; ⑥(+3)+0=%// //%.
(2)有理数的减法法则:减去一个数,等于加上这个数的%////% .
①9-(-5)=%// //%; ②0-6=%// //%;
③|-3|-(-8)=%// //%; ④(-2)-(-1)=%// //%.
相反数
13
-13
2
5
-5
3
14
-6
12
(3)有理数加减混合运算关键是%////% .
①(+12)-(+18)-(+23)+(+51); ②()-().
化成代数和的形式
解:原式=12-18-23+51
=(12+51)-23-18
=63-23-18
=40-18
=22.
解:原式=
=)
=1.
(4)有理数的乘法:
①-6×2=%// //%;
②(-)×(-)=%// //%;
③0×(-)=%// //%;
④()×(-2)=%// //%;
⑤-2.5×0.02=%// //%;
⑥(-)×(-)×(-)=%// //%;
-12
3
0
-0.05
(5)有理数的除法:
①÷(-); ②0÷(-0.52);
③(-3)÷[(-1)÷].
解:原式=×(-7)
=-1.
解:原式=0.
解:原式=(-3)÷(×)
=-3÷()
=(-3)×()=.
(6)有理数的乘方
①(-2)4=%// //%; -24=%// //%; 32=%// //%; (-3)2=%// //%;
②(-)3=%// //%; -=%// //%; (-1)1000=%////%; (-1)2005=%// //%
16
-16
9
9
1
-1
(7)有理数的混合运算:先算%// //%,再算%// //%,最后算%// //%;如果有括号,先算%// //%.
①16÷(-2)3-(-)×(-4)+(-1)2020;②-14-(1-0.5)××[2-(-3)2].
解:原式=16÷(-8)-+1
=-2-+1
=-1.
解:原式=-1-×(2-9)
=-1+
=.
乘方
乘除
加减
括号里面的
【例题1】新型冠状病毒疫情控制期间,大家响应政府号召,防止疫情扩散,人们出行必须佩戴口罩,据不完全统计,天津市每天需要一次性医用口罩约154000个.将154000用科学记数法表示应为(%////%)
A.0.154×106 B.1.54×105
C.15.4×104 D.154×103
B
【例题1】观察下列等式:31=3,32=9,33=27,34=81,
35=243,36=729,…,试猜想,32016的个位数字是%////%.
过关练习1:如图,下面每个图形中的四个数都是按相同的规律填写的,根据此规律确定x的值为%// //%.
1
370
过关练习2:观察下列等式:
第一层1+2=3
第二层4+5+6=7+8
第三层9+10+11+12=13+14+15
第四层16+17+18+19+20=21+22+23+24
…
在上述的数字宝塔中,从上往下数,2017在第%// //%层.
44
1.下列说法中,错误的是(%////%)
A.整数和分数统称有理数
B.整数分为正整数和负整数
C.分数分为正分数和负分数
D.0既不是正数,也不是负数
B
2.下列所画的数轴中,正确的是(%////%)
C
3. 4÷×=%////% .
9
4. 15÷(-)=%// //% .
-112.5
1.(3分)中国人很早开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入负数.如果收入100元记作+100元.那么-80元表示(%////%)
A.支出20元 B.收入20元
C.支出80元 D.收入80元
C
2.(3分)下列说法正确的是(%////%)
A.分数都是有理数
B.-a是负数
C.有理数不是正数就是负数
D.绝对值等于本身的数是正数
A
3.(3分)计算(-2)-5的结果等于(%////%)
A.-7 B.-3 C.3 D.7
A
4.(3分)-的倒数是(%////%)
A.-2 B.2
C. D.-
A
5.(3分)据统计,2015年“十 一”国庆长假期间,衢州市共接待国内外游客约319万人次,与2014年同比增长16.43%,数据319万用科学记数法表示为(%////%)
A.3.19×105 B.3.19×106 C.0.319×107 D.319×106
B
6.(3分)13世纪数学家斐波那契的《计算书》中有这样一个问题:“在罗马有7位老妇人,每人赶着7头毛驴,每头驴驮着7只口袋,每只口袋里装着7个面包,每个面包附有7把餐刀,每把餐刀有7只刀鞘”,则刀鞘数为(%////%)
A.42 B.49 C.76 D.77
C
7.(3分)有理数a,b在数轴上的位置如图所示,在-a,b-a,a+b,0中,最大的是(%////%)
A.-a B.0 C.a+b D.b-a
D
8.(3分)若|x-3|+|y+2|=0,则|x|+|y|=%////%.
5
9.(3分)计算1-2+3-4+5-6+…+2015-2016的
结果是% ////%.
-1008
10.(3分)把下列各数填入它所属的集合内:
5.2,0,,,+(-4),-2,-(-3),0.25555…,-0.030030003…
分数集合:{%// //% };
非负整数集合:{%// //% };
有理数集合:{%// //% }.
5.2,,-2,0.25555…
0,-(-3)
5.2,0,,+(-4),-2,-(-3),0.25555…
11.(6分)计算:
(1)-3-[-5-(1-0.2÷)÷(-2)];
(2)-32×(-)2+(-+)×(-24).
解:原式=-3-[-5-(1-)÷(-2)]
=-3-[-5-×()]
=-3-(-5+)=1.
解:原式=-9×+(-18+4-9)
=-1-18+4-9
=-24.
12.(4分)有一张厚度为0.1毫米的纸片,对折1次后的厚度是2×0.1毫米.
(1)对折2次的厚度是多少毫米?
(2)假设这张纸能无限地折叠下去,那么对折20次后相当于每层高度为3米的楼房多少层?
解:(1)根据题意得:2×2×0.1=0.4毫米,则对折2次的厚度是0.4毫米;
(2)对折20次的厚度为220×0.1=104857.6毫米≈104.9 m,104.9÷3≈35层,
则对折20次后相当于每层高度为3米的楼房35层.
13.(4分)一辆货车为一家商场的仓库运货,仓库在记录进出货物时把运进记作正数,运出记作负数下午记录如下(单位:吨):5.5,-4.6,-5.3,5.4,-3.4,4.8,-3.
(1)仓库上午存货物60吨,下午运完货物后存货多少吨?
(2)如果货车的运费为每吨10元,那么下午货车共得运费多少元?
/解:(1)60+5.5-4.6-5.3+5.4-3.4+4.8-3=59.4(吨),
则下午运完货物后存货59.4吨;
(2)(5.5+4.6+5.3+5.4+3.4+4.8+3)×10=32×10=320(元),则下午货车共得运费320元.
14.(6分)有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
(1)20筐白菜中,最重的一筐比最轻的一筐重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.6元,则出售这20筐白菜可卖多少元?(结果保留整数)
与标准质量的差值(单位:千克) -3 -2 -1.5 0 1 2.5
筐数 1 4 2 3 2 8
解:(1)最重的一筐超过2.5千克,最轻的差3千克,求差即可2.5-(-3)=5.5(千克),
故最重的一筐比最轻的一筐重5.5千克;
(2)列式1×(-3)+4×(-2)+2×(-1.5)+3×0+1×2+8×2.5=-3-8-3+2+20=8(千克),
故20筐白菜总计超过8千克;
(3)用(2)的结果列式计算2.6×(25×20+8)=1320.8≈1321(元),故这20筐白菜可卖1321元.
第二章 有理数及其运算
单元复习
北师大版七年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
资料简介
【问题1】请你构思一个生活中的场景,使其尽可能多地包含负数、数轴、绝对值?
【问题2】举例说明你是怎样获得有理数加法或减法的运算法则的运算内容?
【问题3】有理数有哪些运算法则和运算律?
【问题4】有理数的运算与小学学过的有关数的运算有什么联系?你能举例说明吗?
【问题5】生活中你遇到过用科学记数法表示的“大数”吗?你能举例说明吗?
【问题6】梳理本章内容,用适当的方式(可以用表格、思维导图、列要点)呈现全章知识结构.
【例题1】《九章算术》中有注:“今两算得失相反,要令正负以名之.”意思是:“今有两数若其意义相反,则分别叫做正数和负数.”如果水位升高5米记为+5米,那么水位下降3米应记为(%////%)
A.-5米 B.+5米 C.-2米 D.-3米
D
【例题2】将下列各数填入相应的大括号里.
-,0.618,-3.14,260,-2,,-0.010010001…(每相邻两个1之间依次多一个0),0,.
正数集合:{%// //% };
负数集合:{%// };
整数集合:{%// //% };
分数集合:{%// //% };
0.618,260,,
,-3.14,-2,-0.010010001…
260,-2,0
,0.618,-3.14,,
(1)相反数:只有%/// /%不同的两个数,则称其中一个是另一个的相反数.
(2)倒数:乘积是%////%的两个数互为倒数.
(3)绝对值:数轴上,一个数所对应的点到%// //%的距离.
【例题1】(1)-2020的相反数是:%// / /%;倒数是%// //%;绝对值是%// //%.
(2)x(x≠0)的相反数是:%////%;倒数是%////%;绝对值是%////%.
2020
2020
-x
|x|
符号
1
原点
过关练习1:
-6的相反数是%////%; -(-6)的相反数是%////%;
-[+(-6)]=%/// /%; 0的相反数是%//// %.
6
-6
6
0
过关练习2:
(1)a的倒数是%////%(a≠0);
(2)若a与b互为倒数,则%// //%;倒数是它本身的是%// //%.
(3)-的相反数的倒数是%////%.
ab=1
1和-1
6
过关练习3:
(1)-4的绝对值表示它离开原点的距离是%////个单位,记作// %.
(2)|-6|=%////%;-|-6|=%////%;绝对值等于6的数是%////%.
(3)绝对值等于其相反数的数是%// //%.
(4)绝对值不大于11的整数有
% // //%.
4
|-4|
6
-6
±6
负数或0
0,±1,±2,±3,±4,±5,±6,±7,±8,±9,±10
规定了%// //%、%// //%和%// //%的一条%// //%.
原点
正方向
单位长度
直线
【例题1】把下列各数表示在如图所示数轴上,然后把这些数按从大到小的顺序用“>”连接起来.
0,1,-3,-(-0.5),-|-|,+(-4).
根据数轴的特点把这些数按从大到小的顺序用“>”连接起来为:
1>(-0.5)>0>-||>-3>+(-4).
【例题2】实数a,b在数轴上的对应点的位置如图所示,则正确的结论是(%////%)
A.a>-2 B.a<-3 C.a>-b D.a<-b
D
过关练习1:如图,数轴的单位长度为1,如果点A表示的数是-3,那么点B表示的数是(%////%)
A.0 B.1 C.2 D.3
过关练习2:点A,B在数轴上的位置如图所示,如果点C也在数轴上,且B和C两点间的距离是1,那么AC长度为%// //%.
B
2或4
【例题1】下列各数中,最小的数是(%////%)
A.-3 B.|-2| C.(-3)2 D.2×10-5
A
【例题2】比较大小:%////%-0.009; -%////%-.
>
<
(1)有理数的加法
①(+5)+(+8)=%// //%; ②(-5)+(-8)=%// //%;
③(+12)+(-10)=%// //%; ④2+3=%// //%;
⑤(-2)+(-3)=%// //%; ⑥(+3)+0=%// //%.
(2)有理数的减法法则:减去一个数,等于加上这个数的%////% .
①9-(-5)=%// //%; ②0-6=%// //%;
③|-3|-(-8)=%// //%; ④(-2)-(-1)=%// //%.
相反数
13
-13
2
5
-5
3
14
-6
12
(3)有理数加减混合运算关键是%////% .
①(+12)-(+18)-(+23)+(+51); ②()-().
化成代数和的形式
解:原式=12-18-23+51
=(12+51)-23-18
=63-23-18
=40-18
=22.
解:原式=
=)
=1.
(4)有理数的乘法:
①-6×2=%// //%;
②(-)×(-)=%// //%;
③0×(-)=%// //%;
④()×(-2)=%// //%;
⑤-2.5×0.02=%// //%;
⑥(-)×(-)×(-)=%// //%;
-12
3
0
-0.05
(5)有理数的除法:
①÷(-); ②0÷(-0.52);
③(-3)÷[(-1)÷].
解:原式=×(-7)
=-1.
解:原式=0.
解:原式=(-3)÷(×)
=-3÷()
=(-3)×()=.
(6)有理数的乘方
①(-2)4=%// //%; -24=%// //%; 32=%// //%; (-3)2=%// //%;
②(-)3=%// //%; -=%// //%; (-1)1000=%////%; (-1)2005=%// //%
16
-16
9
9
1
-1
(7)有理数的混合运算:先算%// //%,再算%// //%,最后算%// //%;如果有括号,先算%// //%.
①16÷(-2)3-(-)×(-4)+(-1)2020;②-14-(1-0.5)××[2-(-3)2].
解:原式=16÷(-8)-+1
=-2-+1
=-1.
解:原式=-1-×(2-9)
=-1+
=.
乘方
乘除
加减
括号里面的
【例题1】新型冠状病毒疫情控制期间,大家响应政府号召,防止疫情扩散,人们出行必须佩戴口罩,据不完全统计,天津市每天需要一次性医用口罩约154000个.将154000用科学记数法表示应为(%////%)
A.0.154×106 B.1.54×105
C.15.4×104 D.154×103
B
【例题1】观察下列等式:31=3,32=9,33=27,34=81,
35=243,36=729,…,试猜想,32016的个位数字是%////%.
过关练习1:如图,下面每个图形中的四个数都是按相同的规律填写的,根据此规律确定x的值为%// //%.
1
370
过关练习2:观察下列等式:
第一层1+2=3
第二层4+5+6=7+8
第三层9+10+11+12=13+14+15
第四层16+17+18+19+20=21+22+23+24
…
在上述的数字宝塔中,从上往下数,2017在第%// //%层.
44
1.下列说法中,错误的是(%////%)
A.整数和分数统称有理数
B.整数分为正整数和负整数
C.分数分为正分数和负分数
D.0既不是正数,也不是负数
B
2.下列所画的数轴中,正确的是(%////%)
C
3. 4÷×=%////% .
9
4. 15÷(-)=%// //% .
-112.5
1.(3分)中国人很早开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入负数.如果收入100元记作+100元.那么-80元表示(%////%)
A.支出20元 B.收入20元
C.支出80元 D.收入80元
C
2.(3分)下列说法正确的是(%////%)
A.分数都是有理数
B.-a是负数
C.有理数不是正数就是负数
D.绝对值等于本身的数是正数
A
3.(3分)计算(-2)-5的结果等于(%////%)
A.-7 B.-3 C.3 D.7
A
4.(3分)-的倒数是(%////%)
A.-2 B.2
C. D.-
A
5.(3分)据统计,2015年“十 一”国庆长假期间,衢州市共接待国内外游客约319万人次,与2014年同比增长16.43%,数据319万用科学记数法表示为(%////%)
A.3.19×105 B.3.19×106 C.0.319×107 D.319×106
B
6.(3分)13世纪数学家斐波那契的《计算书》中有这样一个问题:“在罗马有7位老妇人,每人赶着7头毛驴,每头驴驮着7只口袋,每只口袋里装着7个面包,每个面包附有7把餐刀,每把餐刀有7只刀鞘”,则刀鞘数为(%////%)
A.42 B.49 C.76 D.77
C
7.(3分)有理数a,b在数轴上的位置如图所示,在-a,b-a,a+b,0中,最大的是(%////%)
A.-a B.0 C.a+b D.b-a
D
8.(3分)若|x-3|+|y+2|=0,则|x|+|y|=%////%.
5
9.(3分)计算1-2+3-4+5-6+…+2015-2016的
结果是% ////%.
-1008
10.(3分)把下列各数填入它所属的集合内:
5.2,0,,,+(-4),-2,-(-3),0.25555…,-0.030030003…
分数集合:{%// //% };
非负整数集合:{%// //% };
有理数集合:{%// //% }.
5.2,,-2,0.25555…
0,-(-3)
5.2,0,,+(-4),-2,-(-3),0.25555…
11.(6分)计算:
(1)-3-[-5-(1-0.2÷)÷(-2)];
(2)-32×(-)2+(-+)×(-24).
解:原式=-3-[-5-(1-)÷(-2)]
=-3-[-5-×()]
=-3-(-5+)=1.
解:原式=-9×+(-18+4-9)
=-1-18+4-9
=-24.
12.(4分)有一张厚度为0.1毫米的纸片,对折1次后的厚度是2×0.1毫米.
(1)对折2次的厚度是多少毫米?
(2)假设这张纸能无限地折叠下去,那么对折20次后相当于每层高度为3米的楼房多少层?
解:(1)根据题意得:2×2×0.1=0.4毫米,则对折2次的厚度是0.4毫米;
(2)对折20次的厚度为220×0.1=104857.6毫米≈104.9 m,104.9÷3≈35层,
则对折20次后相当于每层高度为3米的楼房35层.
13.(4分)一辆货车为一家商场的仓库运货,仓库在记录进出货物时把运进记作正数,运出记作负数下午记录如下(单位:吨):5.5,-4.6,-5.3,5.4,-3.4,4.8,-3.
(1)仓库上午存货物60吨,下午运完货物后存货多少吨?
(2)如果货车的运费为每吨10元,那么下午货车共得运费多少元?
/解:(1)60+5.5-4.6-5.3+5.4-3.4+4.8-3=59.4(吨),
则下午运完货物后存货59.4吨;
(2)(5.5+4.6+5.3+5.4+3.4+4.8+3)×10=32×10=320(元),则下午货车共得运费320元.
14.(6分)有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
(1)20筐白菜中,最重的一筐比最轻的一筐重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.6元,则出售这20筐白菜可卖多少元?(结果保留整数)
与标准质量的差值(单位:千克) -3 -2 -1.5 0 1 2.5
筐数 1 4 2 3 2 8
解:(1)最重的一筐超过2.5千克,最轻的差3千克,求差即可2.5-(-3)=5.5(千克),
故最重的一筐比最轻的一筐重5.5千克;
(2)列式1×(-3)+4×(-2)+2×(-1.5)+3×0+1×2+8×2.5=-3-8-3+2+20=8(千克),
故20筐白菜总计超过8千克;
(3)用(2)的结果列式计算2.6×(25×20+8)=1320.8≈1321(元),故这20筐白菜可卖1321元.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
