【五环分层导学-课件】4-6 角的比较(2)-北师大版数学七(上)
文档属性
| 名称 | 【五环分层导学-课件】4-6 角的比较(2)-北师大版数学七(上) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-02 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
第四章 基本平面图形
第6课 角的比较(2)
北师大版七年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈等环节来完成。
资料简介
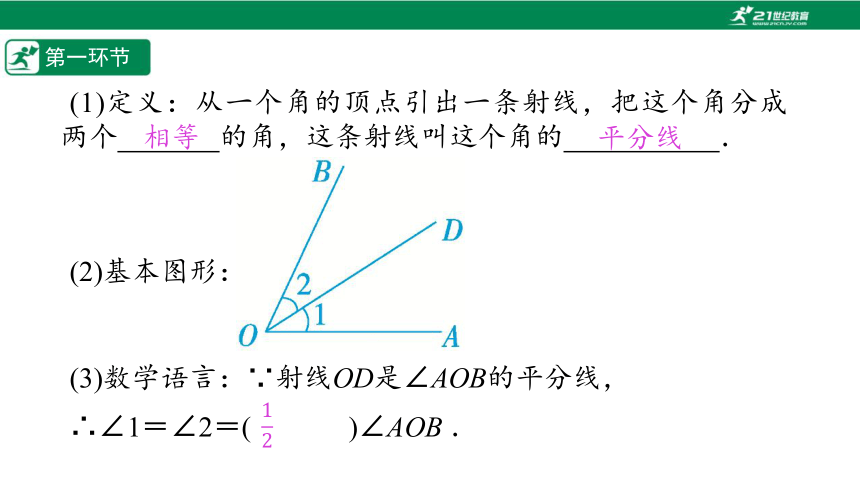
(1)定义:从一个角的顶点引出一条射线,把这个角分成两个%// //%的角,这条射线叫这个角的// %.
(2)基本图形:
(3)数学语言:∵射线OD是∠AOB的平分线,
∴∠1=∠2=(%// //%)∠AOB .
相等
平分线
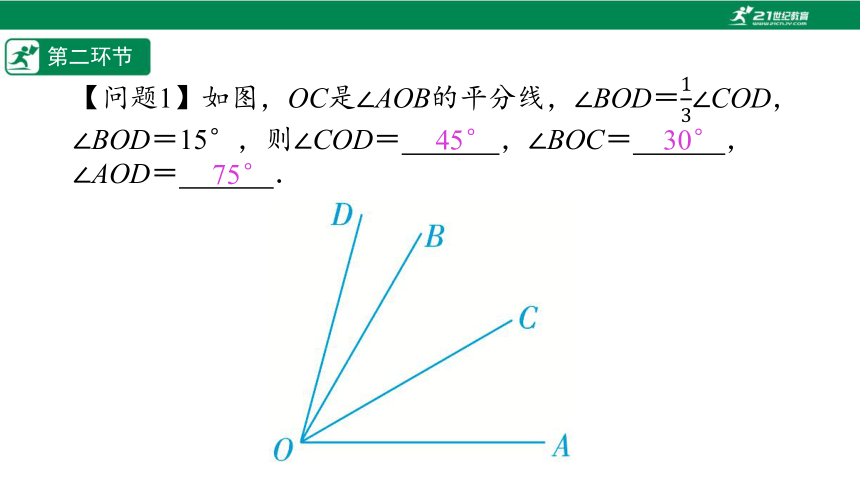
【问题1】如图,OC是∠AOB的平分线,∠BOD=∠COD,∠BOD=15°,则∠COD=%// //%,∠BOC=%// //%,
∠AOD=%// //%.
45°
30°
75°
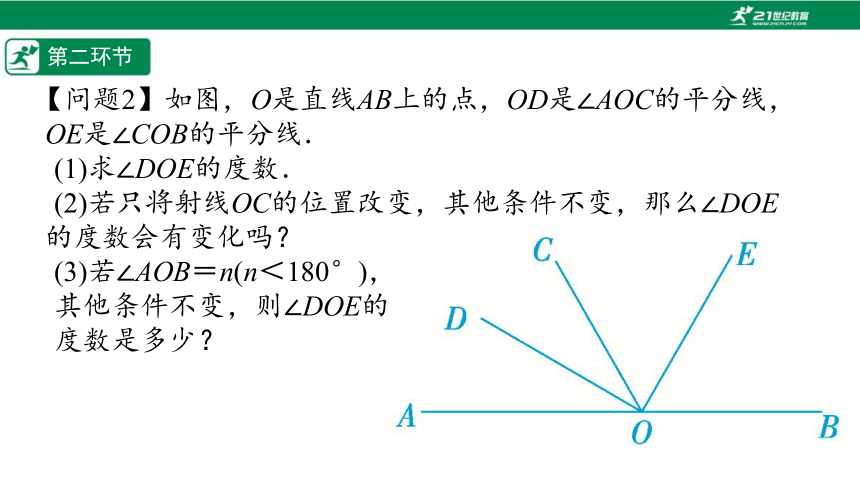
【问题2】如图,O是直线AB上的点,OD是∠AOC的平分线,OE是∠COB的平分线.
(1)求∠DOE的度数.
(2)若只将射线OC的位置改变,其他条件不变,那么∠DOE的度数会有变化吗?
(3)若∠AOB=n(n<180°),
其他条件不变,则∠DOE的
度数是多少?
解:(1)∵OD是∠AOC的平分线,OE是∠COB的平分线.
∴∠AOD=∠COD,∠BOE=∠COE,
∵∠AOB=180°,∴∠DOE=∠COD+∠COE=90°;
(2)由(1)中可知,∠DOE大小和射线OC无关,
∴只将射线OC的位置改变,其他条件不变,
那么∠DOE的度数不会有变化;
(3)∵OD是∠AOC的平分线,OE是∠COB的平分线.
∴∠AOD=∠COD,∠BOE=∠COE,
∵∠AOB=n,∴∠DOE=∠COD+∠COE.
【问题3】已知∠AOB=3∠BOC,若∠BOC=30°,则∠AOC是多少度?
解:∵∠BOC=30°,∠AOB=3∠BOC,
∴∠AOB=3×30°=90°;
(1)当OC在∠AOB的外侧时,
∠AOC=∠AOB+∠BOC=90°+30°=120°;
(2)当OC在∠AOB的内侧时,
∠AOC=∠AOB-∠BOC=90°-30°=60°.
综上,∠AOC=120°或60°
【问题4】解决问题1-3的过程中,你总结出了那些解题策略?
1.如图所示,OC是∠AOB平分线,OD平分∠AOC,且∠AOB=60°,则∠COD为(%////%)
A.15° B.30°
C.45° D.20°
A
2.已知∠AOB=2∠BOC,若∠BOC=30°,则∠AOC=%// //%.
30°或90°
3.(1)从一个角的顶点出发,把这个角分成%// //%的射线,叫做这个角的平分线.
(2)根据定义作出图①中∠AOB的平分线OC .
解:量得∠AOB= ,那么∠AOC= ,
作图如图②所示:根据所画图形OC是∠AOB的平分线,
则∠AOC=∠BOC=%// //%,∠AOB=2%// //%=2%// //%.
两个相等的角
120°
60°
∠AOB
∠AOC
∠BOC
4.如图,OB是∠AOC的角平分线,OD是∠COE的角平分线.
(1)∠AOC=%// //%+%// //%;∠BOD=%// //%+%/ / //%;
∠DOE=% // //%-%// // %;∠AOB=%// //%-%// //%;
(2)如果∠AOB=40°,∠DOE=30°,
那么∠BOD是多少度?
(3)如果∠AOE=140°,∠COD=30°,
那么∠AOB是多少度?
∠AOB
∠BOC
∠BOC
∠COD
∠COE
∠COD
∠AOC
∠BOC
(2)解:∵OB是∠AOC的角平分线,
OD是∠COE的角平分线,
∴∠BOD=∠AOB+∠DOE=40°+30°=70°.
(3)解:∵OD是∠COE的角平分线,
∴∠COD=∠DOE=30°;
∠AOC=∠AOE-∠COE=140°-30°-30°=80°;
∵OB是∠AOC的角平分线,∴∠AOB=∠BOC,
∴∠AOB=∠AOC=40°.
5.如图,从点O引四条射线OA,OB,OC,OD,如果∠AOB∶∠BOC∶∠COD∶∠DOA=1∶2∶3∶4,那么这四个角的度数分别是多少?
解:∵∠AOB∶∠BOC∶∠COD∶∠DOA=1∶2∶3∶4,
又∵∠AOB+∠BOC+∠COD+∠DOA=360°,
∴可设∠AOB=x°,∠BOC=2x°,
∠COD=3x°,∠DOA=4x°,
则x+2x+3x+4x=360,x=36,
∴∠AOB=36°,∠BOC=72°,
∠COD=108°,∠AOD=144°./
6.(★)将两个三角板的两个直角的顶点O重合在一起,放置成如图所示的位置.
(1)如果重叠在一起∠BOC=40°,
猜想∠AOD=%// //%;
(2)如果重叠在一起∠BOC=50°,
猜想∠AOD=%// //%;
(3)在(1)、(2)中,计算∠AOD+∠BOC=%// //%;
(4)由此可知,三角板AOB绕重合点O旋转,不论旋转到任何位置,∠AOD与∠BOC始终满足%// //%的关系;
140°
130°
180°
互补
第四章 基本平面图形
第6课 角的比较(2)
北师大版七年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈等环节来完成。
资料简介
(1)定义:从一个角的顶点引出一条射线,把这个角分成两个%// //%的角,这条射线叫这个角的// %.
(2)基本图形:
(3)数学语言:∵射线OD是∠AOB的平分线,
∴∠1=∠2=(%// //%)∠AOB .
相等
平分线
【问题1】如图,OC是∠AOB的平分线,∠BOD=∠COD,∠BOD=15°,则∠COD=%// //%,∠BOC=%// //%,
∠AOD=%// //%.
45°
30°
75°
【问题2】如图,O是直线AB上的点,OD是∠AOC的平分线,OE是∠COB的平分线.
(1)求∠DOE的度数.
(2)若只将射线OC的位置改变,其他条件不变,那么∠DOE的度数会有变化吗?
(3)若∠AOB=n(n<180°),
其他条件不变,则∠DOE的
度数是多少?
解:(1)∵OD是∠AOC的平分线,OE是∠COB的平分线.
∴∠AOD=∠COD,∠BOE=∠COE,
∵∠AOB=180°,∴∠DOE=∠COD+∠COE=90°;
(2)由(1)中可知,∠DOE大小和射线OC无关,
∴只将射线OC的位置改变,其他条件不变,
那么∠DOE的度数不会有变化;
(3)∵OD是∠AOC的平分线,OE是∠COB的平分线.
∴∠AOD=∠COD,∠BOE=∠COE,
∵∠AOB=n,∴∠DOE=∠COD+∠COE.
【问题3】已知∠AOB=3∠BOC,若∠BOC=30°,则∠AOC是多少度?
解:∵∠BOC=30°,∠AOB=3∠BOC,
∴∠AOB=3×30°=90°;
(1)当OC在∠AOB的外侧时,
∠AOC=∠AOB+∠BOC=90°+30°=120°;
(2)当OC在∠AOB的内侧时,
∠AOC=∠AOB-∠BOC=90°-30°=60°.
综上,∠AOC=120°或60°
【问题4】解决问题1-3的过程中,你总结出了那些解题策略?
1.如图所示,OC是∠AOB平分线,OD平分∠AOC,且∠AOB=60°,则∠COD为(%////%)
A.15° B.30°
C.45° D.20°
A
2.已知∠AOB=2∠BOC,若∠BOC=30°,则∠AOC=%// //%.
30°或90°
3.(1)从一个角的顶点出发,把这个角分成%// //%的射线,叫做这个角的平分线.
(2)根据定义作出图①中∠AOB的平分线OC .
解:量得∠AOB= ,那么∠AOC= ,
作图如图②所示:根据所画图形OC是∠AOB的平分线,
则∠AOC=∠BOC=%// //%,∠AOB=2%// //%=2%// //%.
两个相等的角
120°
60°
∠AOB
∠AOC
∠BOC
4.如图,OB是∠AOC的角平分线,OD是∠COE的角平分线.
(1)∠AOC=%// //%+%// //%;∠BOD=%// //%+%/ / //%;
∠DOE=% // //%-%// // %;∠AOB=%// //%-%// //%;
(2)如果∠AOB=40°,∠DOE=30°,
那么∠BOD是多少度?
(3)如果∠AOE=140°,∠COD=30°,
那么∠AOB是多少度?
∠AOB
∠BOC
∠BOC
∠COD
∠COE
∠COD
∠AOC
∠BOC
(2)解:∵OB是∠AOC的角平分线,
OD是∠COE的角平分线,
∴∠BOD=∠AOB+∠DOE=40°+30°=70°.
(3)解:∵OD是∠COE的角平分线,
∴∠COD=∠DOE=30°;
∠AOC=∠AOE-∠COE=140°-30°-30°=80°;
∵OB是∠AOC的角平分线,∴∠AOB=∠BOC,
∴∠AOB=∠AOC=40°.
5.如图,从点O引四条射线OA,OB,OC,OD,如果∠AOB∶∠BOC∶∠COD∶∠DOA=1∶2∶3∶4,那么这四个角的度数分别是多少?
解:∵∠AOB∶∠BOC∶∠COD∶∠DOA=1∶2∶3∶4,
又∵∠AOB+∠BOC+∠COD+∠DOA=360°,
∴可设∠AOB=x°,∠BOC=2x°,
∠COD=3x°,∠DOA=4x°,
则x+2x+3x+4x=360,x=36,
∴∠AOB=36°,∠BOC=72°,
∠COD=108°,∠AOD=144°./
6.(★)将两个三角板的两个直角的顶点O重合在一起,放置成如图所示的位置.
(1)如果重叠在一起∠BOC=40°,
猜想∠AOD=%// //%;
(2)如果重叠在一起∠BOC=50°,
猜想∠AOD=%// //%;
(3)在(1)、(2)中,计算∠AOD+∠BOC=%// //%;
(4)由此可知,三角板AOB绕重合点O旋转,不论旋转到任何位置,∠AOD与∠BOC始终满足%// //%的关系;
140°
130°
180°
互补
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
