【五环分层导学-课件】4-8 单元复习 基本平面图形-北师大版数学七(上)
文档属性
| 名称 | 【五环分层导学-课件】4-8 单元复习 基本平面图形-北师大版数学七(上) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-02 00:00:00 | ||
图片预览









文档简介
(共37张PPT)
第四章 基本平面图形
单元复习
北师大版七年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
资料简介
【问题1】生活中有哪些你熟悉的平面图形?举例说明.
【问题2】找一找生活中你喜欢的图案,说说它是由哪些基本几何图形组成的.
【问题3】选择几种基本几何图形设计一个你喜欢的图案,说明寓意并与同伴交流.
【问题4】通过本章的学习,你知道了哪些比较线段长短的方法?比较角的大小呢?它们间有什么相似之处?
【问题5】梳理本章内容,用适当的方式(可以用表格、思维导图、列要点)呈现全章知识结构.
考点1:线段、射线、直线
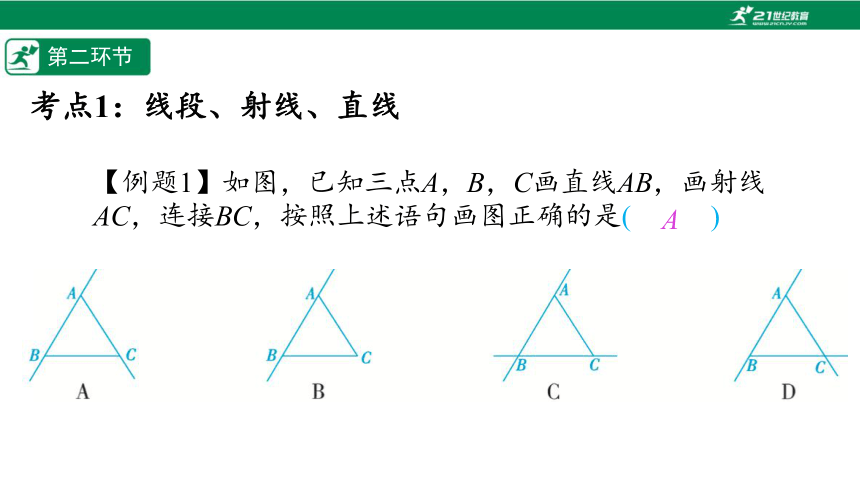
【例题1】如图,已知三点A,B,C画直线AB,画射线AC,连接BC,按照上述语句画图正确的是(%////%)
A
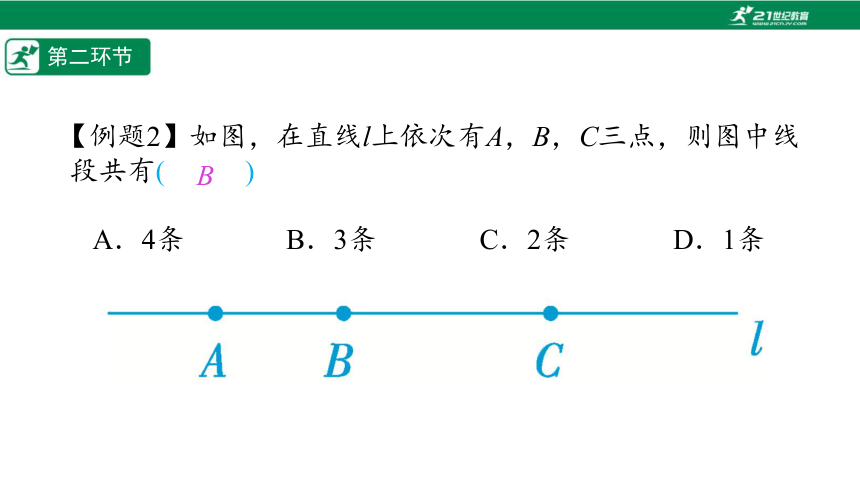
【例题2】如图,在直线l上依次有A,B,C三点,则图中线段共有(%////%)
A.4条 B.3条 C.2条 D.1条
B
【例题3】如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是(%////%)
A.垂线段最短
B.经过一点有无数条直线
C.经过两点,有且仅有一条直线
D.两点之间,线段最短
D
考点2:中点与线段的计算
【例题1】如图,AB=CD,那么AC与BD的大小关系是(%////%)
A.AC=BD B.AC<BD C.AC>BD D.不能确定
A
【例题2】如图,点C、D是线段AB上的两点,点D是线段AC的中点.若AB=10 cm,BC=4 cm,则线段DB的长等于(%////%)
A.2 cm B.3 cm C.6 cm D.7 cm
D
【例题3】如图,AB=18,C为AB的中点,点D在线段AC上,且AD∶CB=1∶3,则DB的长度是(%////%)
A.8 B.10 C.12 D.15
D
考点3:角的相关概念
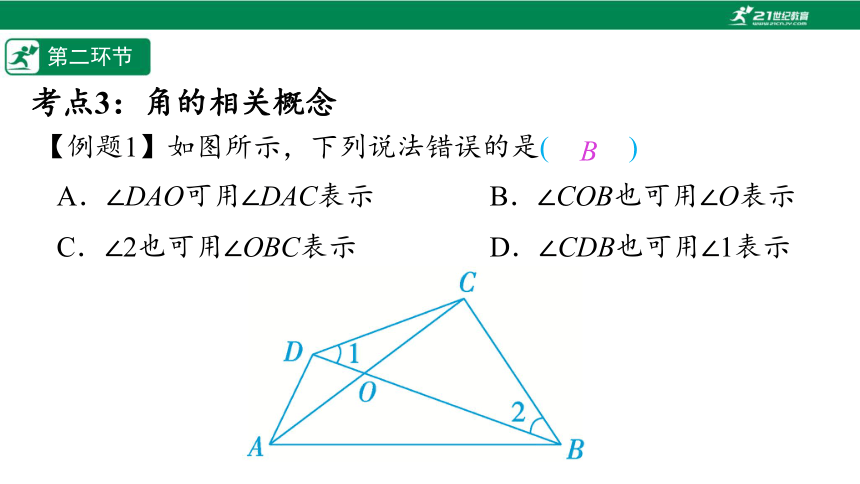
【例题1】如图所示,下列说法错误的是(%////%)
A.∠DAO可用∠DAC表示 B.∠COB也可用∠O表示
C.∠2也可用∠OBC表示 D.∠CDB也可用∠1表示
B
【例题2】如图,已知轮船甲在A处沿北偏东65°的方向匀速航行,同时轮船乙在轮船甲的南偏东40°方向的点B处沿某一方向航行,速度与甲轮船的速度相同.若经过一段时间后,两艘轮船恰好相遇,则轮船乙的航行方向为(%////%)
A.北偏西40°
B.北偏东40°
C.北偏西35°
D.北偏东35°
D
【例题3】当钟表上显示1点30分时,时针与分针所成夹角的度数为(%////%)
A.130° B.135° C.150° D.210°
B
考点4:角平分线与计算
【例题1】若∠1=40.4°,∠2=40°4′,则∠1与∠2的大小关系是(%////%)
A.∠1<∠2 B.∠1>∠2
C.∠1=∠2 D.无法确定
B
【例题2】如图,O为直线AC上一点,OD是∠AOB的平分线,OE在∠BOC的内部,∠BOE=∠BOC,∠DOE=72°,∠EOC的度数%// //%.
72°
【例题3】如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为%// //%.
70°
考点5:多边形和圆(扇形)
【例题1】从十二边形的一个顶点出发,可引出对角线有(%////%)
A.9条 B.10条 C.11条 D.12条
A
【例题2】扇子是引风用品,夏令营必备之物,纸扇在DE与BC之间糊有纸条,可以题字或者作画.如图,竹条AD的长为5 cm,贴纸的部分BD的长为10 cm.扇形纸扇完全打开后,外侧两竹条AB,AC夹角为120°,则纸扇贴纸部分的面积为(%////%)
A.πcm2 B.πcm2
C.πcm2 D.100πcm2
C
1.下列语句正确的有(%////%)
①画直线AB;
②因为直线AB与直线BA是同一条直线,所以射线AB与射线BA是同一条射线;
③延长射线OA;
④线段AB与线段BA是同一条线段.
A.0个 B.1个 C.2个 D.3个
C
2.如图中角的表示方法正确的个数有(%////%)
A.1个 B.2个 C.3个 D.4个
B
3.下列四种说法:
①因为AM=MB,所以M是AB中点;
②在线段AM的延长线上取一点B,如果AB=2AM,那么M是AB的中点;
③因为M是AB的中点,所以AM=MB=AB;
④因为A、M、B在同一条直线上,且AM=BM,所以M是AB中点
其中正确的是(%////%)
A.①③④ B.④ C.②③④ D.③④
C
4.下列说法中,能说明射线OP为∠AOB的平分线的有(%////%)
①∠AOP=∠BOP; ②∠AOP=∠AOB;
③∠AOB=2∠AOP;
④∠AOB=∠AOP+∠BOP; ⑤∠AOP=∠BOP=∠AOB .
A.①②③⑤ B.①②③ C.①④⑤ D.⑤
D
5.已知在平面内,∠AOB=70°,∠BOC=40°,求∠AOC的度数.
解:分两种情况考虑:
(1)当∠BOC在∠AOB外部时,
∠AOC=∠AOB+∠BOC=70°+40°=110°;
(2)当∠BOC在∠AOB内部时,
∠AOC=∠AOB-∠BOC=70°-40°=30°;
则∠AOC的度数为110°或30°.
1.(3分)下列说法正确的是(%////%)
A.过一点P只能作一条直线
B.直线AB和直线BA表示同一条直线
C.射线AB和射线BA表示同一条射线
D.射线a比直线b短
B
2.(3分)下面表示∠ABC的图是(%////%)
C
3.(3分)下列说法正确的是(%////%)
A.连接两点的线段叫做两点的距离
B.线段的中点到线段两个端点的距离相等
C.到线段两个端点距离相等的点叫做线段的中点
D.AB=BC,则点B是线段AC的中点
B
4.(3分)现在的时间是9点30分,时钟面上的时针与分针的夹角是(%////%)
A.90° B.100° C.105° D.107°
C
5.(3分)如图,CO⊥AB,DO是∠AOC的平分线,EO是∠BOC的平分线,则∠DOE的度数是(%////%)
A.89° B.91° C.92° D.90°
D
6.(3分)如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2 cm,AC比BC长(%////%)
A.1 cm B.2 cm C.4 cm D.6 cm
C
7.(3分)如图,圆的四条半径分别是OA,OB,OC,OD,其中点O,A,B在同一条直线上,∠AOD=90°,∠AOC=3∠BOC,那么圆被四条半径分成的四个扇形的面积的比是(%////%)
A.1∶2∶2∶3 B.3∶2∶2∶3
C.4∶2∶2∶3 D.1∶2∶2∶1
A
8.(3分)已知线段AB=5 cm,在直线AB上画线段AC=3 cm,则线段BC的长为(%////%)
A.8 cm B.2 cm或8 cm C.2 cm D.不能确定
B
9.(3分)若将弯曲的河道改直,可以缩短航程,根据是%// //%.
两点之间,线段最短
10.(3分)选定多边形的一个顶点,连接这个顶点和多边形的其余各个顶点,得到了8个三角形,则原多边形的边数是%// //%.
10
11.(6分)如图,C是线段AB上一点,M是AC的中点,N是BC的中点.
(1)若AM=1,BC=4,求MN的长度.
(2)若AB=6,求MN的长度.
解:(1)∵N是BC的中点,M是AC的中点,AM=1,BC=4,
∴CN=2,AM=CM=1,∴MN=MC+CN=3;
(2)∵M是AC的中点,N是BC的中点,AB=6,
∴NM=MC+CNAB=3.
12.(4分)如图,OE为∠AOD的平分线,∠COD=∠EOC,∠COD=15°,求:
(1)∠EOC的大小; (2)∠AOD的大小.
解:(1)由∠COD∠EOC,
得∠EOC=4∠COD=4×15°=60°;
(2)由角的和差,
得∠EOD=∠EOC-∠COD=60°-15°=45°.
由角平分线的性质,得∠AOD=2∠EOD=2×45°=90°.
13.(4分)如图,将一个圆分成4个扇形,已知扇形AOB、AOD、BOD的圆心角的度数之比为2∶3∶4,OC为∠BOD的角平分线,求这4个扇形的圆心角度数.
解:∵OC为∠BOD的角平分线,
∴∠BOC=∠COD,
∵扇形AOB、AOD、BOD的圆心角
的度数之比为2∶3∶4,
∴∠AOB∶∠AOD∶∠COD∶∠BOC=2∶3∶2∶2,
∵∠AOB+∠AOD+∠COD+∠BOC=360°,
∴∠AOB=∠COD=∠BOC=80°,∠AOD=120°.
14.(6分)探索题:如图,线段AB上的点数与线段的总数有如下关系:
如果线段AB上有三个点时,线段总共有3条,如果线段AB上有4个点时,线段总数有6条,如果线段AB上有5个点时,线段总数共有10条,…
(1)当线段AB上有6个点时,线段总数共有%////%条.
(2)当线段AB上有101个点时,线段总数共有多少条?
解:(1)AB上有3个点时,线段总数共有3=条,
AB上有4个点时,线段总数共有6=条,
AB上有5个点时,线段总数共有10=条,
…
AB上有n个点时,线段总数共有:条,
故当线段AB上有6个点时,线段总数共有=15条;
(2)当n=101时,线段总数共有=5050条.
第四章 基本平面图形
单元复习
北师大版七年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
资料简介
【问题1】生活中有哪些你熟悉的平面图形?举例说明.
【问题2】找一找生活中你喜欢的图案,说说它是由哪些基本几何图形组成的.
【问题3】选择几种基本几何图形设计一个你喜欢的图案,说明寓意并与同伴交流.
【问题4】通过本章的学习,你知道了哪些比较线段长短的方法?比较角的大小呢?它们间有什么相似之处?
【问题5】梳理本章内容,用适当的方式(可以用表格、思维导图、列要点)呈现全章知识结构.
考点1:线段、射线、直线
【例题1】如图,已知三点A,B,C画直线AB,画射线AC,连接BC,按照上述语句画图正确的是(%////%)
A
【例题2】如图,在直线l上依次有A,B,C三点,则图中线段共有(%////%)
A.4条 B.3条 C.2条 D.1条
B
【例题3】如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是(%////%)
A.垂线段最短
B.经过一点有无数条直线
C.经过两点,有且仅有一条直线
D.两点之间,线段最短
D
考点2:中点与线段的计算
【例题1】如图,AB=CD,那么AC与BD的大小关系是(%////%)
A.AC=BD B.AC<BD C.AC>BD D.不能确定
A
【例题2】如图,点C、D是线段AB上的两点,点D是线段AC的中点.若AB=10 cm,BC=4 cm,则线段DB的长等于(%////%)
A.2 cm B.3 cm C.6 cm D.7 cm
D
【例题3】如图,AB=18,C为AB的中点,点D在线段AC上,且AD∶CB=1∶3,则DB的长度是(%////%)
A.8 B.10 C.12 D.15
D
考点3:角的相关概念
【例题1】如图所示,下列说法错误的是(%////%)
A.∠DAO可用∠DAC表示 B.∠COB也可用∠O表示
C.∠2也可用∠OBC表示 D.∠CDB也可用∠1表示
B
【例题2】如图,已知轮船甲在A处沿北偏东65°的方向匀速航行,同时轮船乙在轮船甲的南偏东40°方向的点B处沿某一方向航行,速度与甲轮船的速度相同.若经过一段时间后,两艘轮船恰好相遇,则轮船乙的航行方向为(%////%)
A.北偏西40°
B.北偏东40°
C.北偏西35°
D.北偏东35°
D
【例题3】当钟表上显示1点30分时,时针与分针所成夹角的度数为(%////%)
A.130° B.135° C.150° D.210°
B
考点4:角平分线与计算
【例题1】若∠1=40.4°,∠2=40°4′,则∠1与∠2的大小关系是(%////%)
A.∠1<∠2 B.∠1>∠2
C.∠1=∠2 D.无法确定
B
【例题2】如图,O为直线AC上一点,OD是∠AOB的平分线,OE在∠BOC的内部,∠BOE=∠BOC,∠DOE=72°,∠EOC的度数%// //%.
72°
【例题3】如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为%// //%.
70°
考点5:多边形和圆(扇形)
【例题1】从十二边形的一个顶点出发,可引出对角线有(%////%)
A.9条 B.10条 C.11条 D.12条
A
【例题2】扇子是引风用品,夏令营必备之物,纸扇在DE与BC之间糊有纸条,可以题字或者作画.如图,竹条AD的长为5 cm,贴纸的部分BD的长为10 cm.扇形纸扇完全打开后,外侧两竹条AB,AC夹角为120°,则纸扇贴纸部分的面积为(%////%)
A.πcm2 B.πcm2
C.πcm2 D.100πcm2
C
1.下列语句正确的有(%////%)
①画直线AB;
②因为直线AB与直线BA是同一条直线,所以射线AB与射线BA是同一条射线;
③延长射线OA;
④线段AB与线段BA是同一条线段.
A.0个 B.1个 C.2个 D.3个
C
2.如图中角的表示方法正确的个数有(%////%)
A.1个 B.2个 C.3个 D.4个
B
3.下列四种说法:
①因为AM=MB,所以M是AB中点;
②在线段AM的延长线上取一点B,如果AB=2AM,那么M是AB的中点;
③因为M是AB的中点,所以AM=MB=AB;
④因为A、M、B在同一条直线上,且AM=BM,所以M是AB中点
其中正确的是(%////%)
A.①③④ B.④ C.②③④ D.③④
C
4.下列说法中,能说明射线OP为∠AOB的平分线的有(%////%)
①∠AOP=∠BOP; ②∠AOP=∠AOB;
③∠AOB=2∠AOP;
④∠AOB=∠AOP+∠BOP; ⑤∠AOP=∠BOP=∠AOB .
A.①②③⑤ B.①②③ C.①④⑤ D.⑤
D
5.已知在平面内,∠AOB=70°,∠BOC=40°,求∠AOC的度数.
解:分两种情况考虑:
(1)当∠BOC在∠AOB外部时,
∠AOC=∠AOB+∠BOC=70°+40°=110°;
(2)当∠BOC在∠AOB内部时,
∠AOC=∠AOB-∠BOC=70°-40°=30°;
则∠AOC的度数为110°或30°.
1.(3分)下列说法正确的是(%////%)
A.过一点P只能作一条直线
B.直线AB和直线BA表示同一条直线
C.射线AB和射线BA表示同一条射线
D.射线a比直线b短
B
2.(3分)下面表示∠ABC的图是(%////%)
C
3.(3分)下列说法正确的是(%////%)
A.连接两点的线段叫做两点的距离
B.线段的中点到线段两个端点的距离相等
C.到线段两个端点距离相等的点叫做线段的中点
D.AB=BC,则点B是线段AC的中点
B
4.(3分)现在的时间是9点30分,时钟面上的时针与分针的夹角是(%////%)
A.90° B.100° C.105° D.107°
C
5.(3分)如图,CO⊥AB,DO是∠AOC的平分线,EO是∠BOC的平分线,则∠DOE的度数是(%////%)
A.89° B.91° C.92° D.90°
D
6.(3分)如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2 cm,AC比BC长(%////%)
A.1 cm B.2 cm C.4 cm D.6 cm
C
7.(3分)如图,圆的四条半径分别是OA,OB,OC,OD,其中点O,A,B在同一条直线上,∠AOD=90°,∠AOC=3∠BOC,那么圆被四条半径分成的四个扇形的面积的比是(%////%)
A.1∶2∶2∶3 B.3∶2∶2∶3
C.4∶2∶2∶3 D.1∶2∶2∶1
A
8.(3分)已知线段AB=5 cm,在直线AB上画线段AC=3 cm,则线段BC的长为(%////%)
A.8 cm B.2 cm或8 cm C.2 cm D.不能确定
B
9.(3分)若将弯曲的河道改直,可以缩短航程,根据是%// //%.
两点之间,线段最短
10.(3分)选定多边形的一个顶点,连接这个顶点和多边形的其余各个顶点,得到了8个三角形,则原多边形的边数是%// //%.
10
11.(6分)如图,C是线段AB上一点,M是AC的中点,N是BC的中点.
(1)若AM=1,BC=4,求MN的长度.
(2)若AB=6,求MN的长度.
解:(1)∵N是BC的中点,M是AC的中点,AM=1,BC=4,
∴CN=2,AM=CM=1,∴MN=MC+CN=3;
(2)∵M是AC的中点,N是BC的中点,AB=6,
∴NM=MC+CNAB=3.
12.(4分)如图,OE为∠AOD的平分线,∠COD=∠EOC,∠COD=15°,求:
(1)∠EOC的大小; (2)∠AOD的大小.
解:(1)由∠COD∠EOC,
得∠EOC=4∠COD=4×15°=60°;
(2)由角的和差,
得∠EOD=∠EOC-∠COD=60°-15°=45°.
由角平分线的性质,得∠AOD=2∠EOD=2×45°=90°.
13.(4分)如图,将一个圆分成4个扇形,已知扇形AOB、AOD、BOD的圆心角的度数之比为2∶3∶4,OC为∠BOD的角平分线,求这4个扇形的圆心角度数.
解:∵OC为∠BOD的角平分线,
∴∠BOC=∠COD,
∵扇形AOB、AOD、BOD的圆心角
的度数之比为2∶3∶4,
∴∠AOB∶∠AOD∶∠COD∶∠BOC=2∶3∶2∶2,
∵∠AOB+∠AOD+∠COD+∠BOC=360°,
∴∠AOB=∠COD=∠BOC=80°,∠AOD=120°.
14.(6分)探索题:如图,线段AB上的点数与线段的总数有如下关系:
如果线段AB上有三个点时,线段总共有3条,如果线段AB上有4个点时,线段总数有6条,如果线段AB上有5个点时,线段总数共有10条,…
(1)当线段AB上有6个点时,线段总数共有%////%条.
(2)当线段AB上有101个点时,线段总数共有多少条?
解:(1)AB上有3个点时,线段总数共有3=条,
AB上有4个点时,线段总数共有6=条,
AB上有5个点时,线段总数共有10=条,
…
AB上有n个点时,线段总数共有:条,
故当线段AB上有6个点时,线段总数共有=15条;
(2)当n=101时,线段总数共有=5050条.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
