【五环分层导学-课件】6-5 统计图的选择-北师大版数学七(上)
文档属性
| 名称 | 【五环分层导学-课件】6-5 统计图的选择-北师大版数学七(上) |

|
|
| 格式 | pptx | ||
| 文件大小 | 17.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-02 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
第六章 数据的收集与整理
第5课 统计图的选择
北师大版七年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈等环节来完成。
资料简介
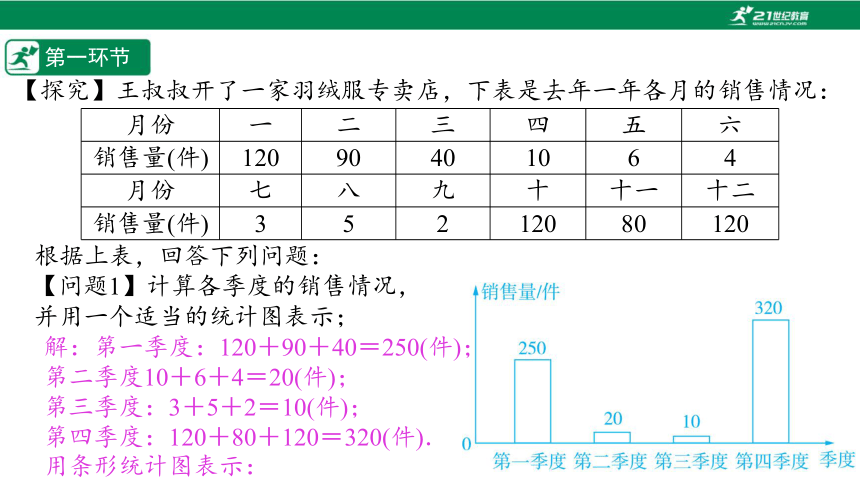
【探究】王叔叔开了一家羽绒服专卖店,下表是去年一年各月的销售情况:
根据上表,回答下列问题:
【问题1】计算各季度的销售情况,
并用一个适当的统计图表示;
月份 一 二 三 四 五 六
销售量(件) 120 90 40 10 6 4
月份 七 八 九 十 十一 十二
销售量(件) 3 5 2 120 80 120
解:第一季度:120+90+40=250(件);
第二季度10+6+4=20(件);
第三季度:3+5+2=10(件);
第四季度:120+80+120=320(件).
用条形统计图表示:
【问题2】计算各季度的销售量在全年销售中所占的百分比,并用适当的统计图表示;
解:用扇形统计图表示:
各季度所占的百分比为:41.7%,3.3%,1.7%,53.3%.
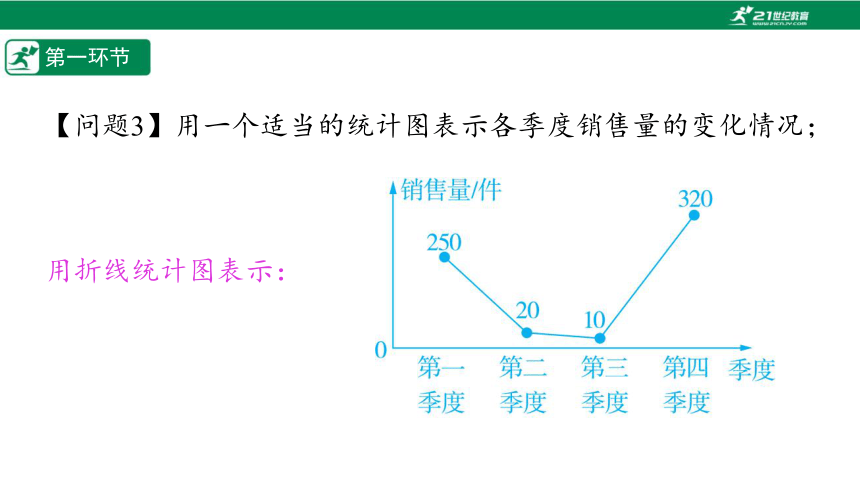
【问题3】用一个适当的统计图表示各季度销售量的变化情况;
用折线统计图表示:
【问题4】从这些统计图表中,你能分别得出什么结论?根据结论你能否针对经营决策向小明提出建议?
【问题5】通过以上活动,我们将如何根据需要选择合适的统计图?
小结:条形统计图能清楚地表示出每个项目的%// //%;折线统计图能清楚地反映出事物的%// //%;扇形统计图能清楚地表示出各部分在总体中所占的%// //%.
答:从图表中可以看到二、三季度的销售量小,一、四季度的销售量大.
根据图示对王叔叔提出合理建议即可,建议:如在11、12月份招聘员工,旺季时多进羽绒服,淡季时转进其它货物或租给别人使用.
答:若要清楚地表示出每个项目的具体数目选择条形统计图;
若要清楚地反映事物的变化情况需选择折线统计图;
若要清楚地表示出各部分在总体中所占的百分比则选择扇形统计图.
具体数目
变化情况
百分比
【例题1】一所中学准备搬迁到新校舍,在这之前,同学们就该校300名学生如何到校问题进行了一次调查,并得到下列数据:
根据下面要求制作统计图:
(1)统计图能清楚地表示每个项目的
具体数目,选择%// //%统计图;
(2)统计图能清楚表示各个部分在总体
中所占的百分比,选择%// //%统计图.
A步行 60人
B骑自行车 100人
C坐公共汽车 130人
D其他 10人
条形
扇形
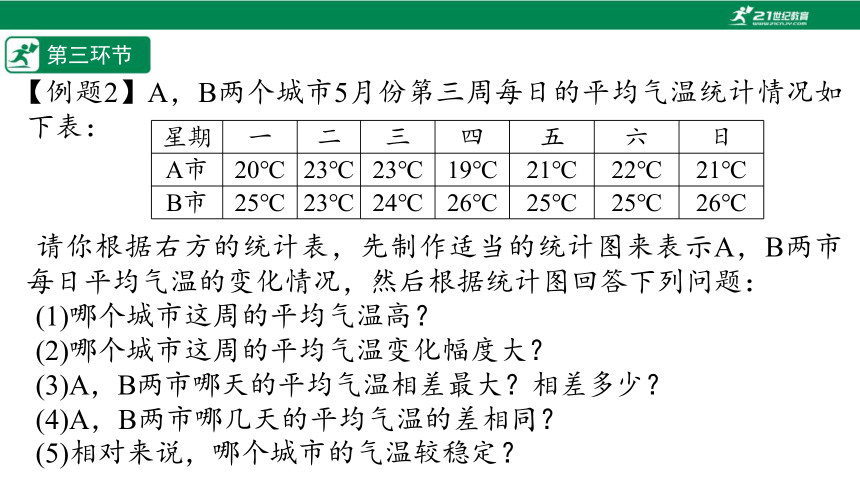
【例题2】A,B两个城市5月份第三周每日的平均气温统计情况如下表:
请你根据右方的统计表,先制作适当的统计图来表示A,B两市每日平均气温的变化情况,然后根据统计图回答下列问题:
(1)哪个城市这周的平均气温高?
(2)哪个城市这周的平均气温变化幅度大?
(3)A,B两市哪天的平均气温相差最大?相差多少?
(4)A,B两市哪几天的平均气温的差相同?
(5)相对来说,哪个城市的气温较稳定?
星期 一 二 三 四 五 六 日
A市 20℃ 23℃ 23℃ 19℃ 21℃ 22℃ 21℃
B市 25℃ 23℃ 24℃ 26℃ 25℃ 25℃ 26℃
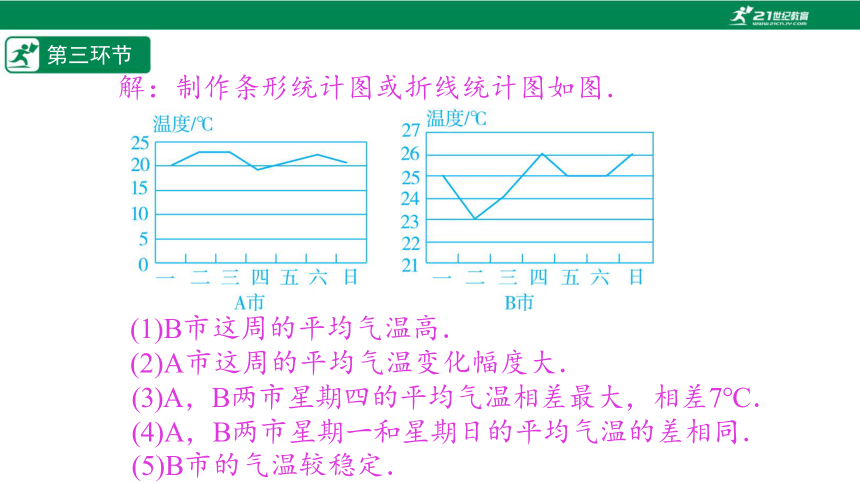
解:制作条形统计图或折线统计图如图.
(1)B市这周的平均气温高.
(2)A市这周的平均气温变化幅度大.
(3)A,B两市星期四的平均气温相差最大,相差7℃.
(4)A,B两市星期一和星期日的平均气温的差相同.
(5)B市的气温较稳定.
1.为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少?”,共有4个选项:
(A)1.5小时以上 (B)1~1.5小时 (C)0.5—1小时 (D)0.5小时以下
图①、②是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
(1)本次一共调查了%// //%名学生;
(2)在图①中将选项B的部分补充完整;
(3)若该校有3000名学生,请你估计
全校平均每天参加体育活动的时间
在0.5小时以下的学生可能有多少名?
解:(1)本次调查活动采取了抽样调查方式;
由图知A类有60人,占30%,则本次一共调查了60÷30%=200人;
200
(2)选B的人数:200×50%=100(人),
选项B的部分补充如图所示:
(3)3000×5%=150(人),
答:估计全校可能有150名学生平均每天参加体育活动的时间在0.5小时以下.
2.保障房建设是民心工程.某市从2008年开始加快保障房建设进程.现统计了该市2008年到2012年这5年新建保障房情况,绘制成如图所示的折线统计图和不完整的条形统计图.
(1)小丽看了统计图后说:“该市2011年新建保障房的套数比2010年少了.”你认为小丽的说法正确吗?请说明理由;
(2)请补全条形统计图;
(3)求这5年平均每年
新建保障房的套数.
解:(1)该市2011年新建保障房的增长率比2010年的增长率减少了,
但是保障房的总数在增加,故小丽的说法错误;
(2)2011年保障房的套数为:
750×(1+20%)=900(套),
设2008年保障房的套数为x,
所以x(1+20%)=600,则x=500,
如图所示:
(3)这5年平均每年新建保障房的套数为:
(500+600+750+900+1170)÷5=784(套),
答:这5年平均每年新建保障房的套数为784套.
3. 2013年3月28日是全国中小学生安全教育日,某校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计.请根据尚未完成的频率分布表和频数分布直方图(如图),解答下列问题:
频率分布表 分数段 频数 频率
50.5~60.5 16 0.08
60.5~70.5 40 0.2
70.5~80.5 50 0.25
80.5~90.5 m 0.35
90.5~100.5 24 n
(1)这次抽取了%////%名学生的竞赛成绩进行统计,
其中:m=%////%,n=%////%;
(2)补全频数分布直方图;
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?
解:(1)抽取的学生数:
16÷0.08=200(名),
m=200-16-40-50-24=70,
n=24÷200=0.12=12%;
(2)如图所示:
(3)1500×=420(人),
答:该校安全意识不强的学生约有420人.
4.(★)甲乙两种酒近几年的销售量和价格如下:
甲品牌酒的产量和价格:
乙品牌酒的产量和价格:
2002年 2006年 2010年
年度销售量(万瓶) 150 180 210
该年度的单价(元) 40 50 60
2006年 2008年 2010年
年度销售量(万瓶) 160 180 200
该年度的单价(元) 40 50 60
有人根据上面的图表,在下图中作出甲乙两种酒的价格变化的折线统计图:
(1)你认为哪一种酒的价格增长较快?为什么?这与上面画出的折线统计图,给你的感觉一致吗?为什么图象会给人这样的感觉?
(2)甲种酒的销售人员将甲种酒的销售信息制作成了如图③的条形统计图:请你在图④中作出甲种酒的年度销售量的条形统计图:
(3)两幅条形统计图给你的感觉一样吗?在甲种酒销售人员画的条形统计图中,2010年甲种酒的年度销售量看上去是2002年的多少倍?实际上呢?
(4)为了较直观地比较某两个统计量的变化速度,绘制折线统计图时,应注意什么?为了较直观地反映几个统计量之间的比例关系,绘制条形统计图时,应注意些什么?
解:(1)甲种酒是从2002年到2010年涨了20元,而乙种酒却是从2006年到2010年涨了20元,显然乙钟酒价格涨得比较快.但是从折线统计图看,似乎甲种酒价格涨得较快.这是因为图①与图②中坐标轴上同一单位长度所表示的意义不一致,图①与图②相比.纵轴(价格)被“拉长”了,横轴(年份)被“压缩”了,结果使得图①中的折线看起来更“陡”了.
(2)如图所示:
(3)图③与图④给人的感觉不一样,在图③中,2010年的销售量看上去是2002年的3倍左右;但根据统计表提供的数据信息,甲种酒2010年的销售量是2002年的1.4倍.人们往往习惯于根据条形统计图中的“柱”的高度来判断相应数值的大小,而图③的纵轴不是从“0”开始的(下面一段被砍掉了),因此“柱”的高度与其相应的数值不成正比,从而给人造成错觉.
(4)若要较为直观地比较两个统计量的变化速度,在绘制折线统计图时,应注意:两个图横轴上同一单位长度所表示的意义应一致,纵轴上同一单位长度所表示的意义也应一致.为了直观地反映几个统计量之间的比例关系,绘制条形统计图时应注意:纵轴上的数值应从0开始.
第六章 数据的收集与整理
第5课 统计图的选择
北师大版七年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈等环节来完成。
资料简介
【探究】王叔叔开了一家羽绒服专卖店,下表是去年一年各月的销售情况:
根据上表,回答下列问题:
【问题1】计算各季度的销售情况,
并用一个适当的统计图表示;
月份 一 二 三 四 五 六
销售量(件) 120 90 40 10 6 4
月份 七 八 九 十 十一 十二
销售量(件) 3 5 2 120 80 120
解:第一季度:120+90+40=250(件);
第二季度10+6+4=20(件);
第三季度:3+5+2=10(件);
第四季度:120+80+120=320(件).
用条形统计图表示:
【问题2】计算各季度的销售量在全年销售中所占的百分比,并用适当的统计图表示;
解:用扇形统计图表示:
各季度所占的百分比为:41.7%,3.3%,1.7%,53.3%.
【问题3】用一个适当的统计图表示各季度销售量的变化情况;
用折线统计图表示:
【问题4】从这些统计图表中,你能分别得出什么结论?根据结论你能否针对经营决策向小明提出建议?
【问题5】通过以上活动,我们将如何根据需要选择合适的统计图?
小结:条形统计图能清楚地表示出每个项目的%// //%;折线统计图能清楚地反映出事物的%// //%;扇形统计图能清楚地表示出各部分在总体中所占的%// //%.
答:从图表中可以看到二、三季度的销售量小,一、四季度的销售量大.
根据图示对王叔叔提出合理建议即可,建议:如在11、12月份招聘员工,旺季时多进羽绒服,淡季时转进其它货物或租给别人使用.
答:若要清楚地表示出每个项目的具体数目选择条形统计图;
若要清楚地反映事物的变化情况需选择折线统计图;
若要清楚地表示出各部分在总体中所占的百分比则选择扇形统计图.
具体数目
变化情况
百分比
【例题1】一所中学准备搬迁到新校舍,在这之前,同学们就该校300名学生如何到校问题进行了一次调查,并得到下列数据:
根据下面要求制作统计图:
(1)统计图能清楚地表示每个项目的
具体数目,选择%// //%统计图;
(2)统计图能清楚表示各个部分在总体
中所占的百分比,选择%// //%统计图.
A步行 60人
B骑自行车 100人
C坐公共汽车 130人
D其他 10人
条形
扇形
【例题2】A,B两个城市5月份第三周每日的平均气温统计情况如下表:
请你根据右方的统计表,先制作适当的统计图来表示A,B两市每日平均气温的变化情况,然后根据统计图回答下列问题:
(1)哪个城市这周的平均气温高?
(2)哪个城市这周的平均气温变化幅度大?
(3)A,B两市哪天的平均气温相差最大?相差多少?
(4)A,B两市哪几天的平均气温的差相同?
(5)相对来说,哪个城市的气温较稳定?
星期 一 二 三 四 五 六 日
A市 20℃ 23℃ 23℃ 19℃ 21℃ 22℃ 21℃
B市 25℃ 23℃ 24℃ 26℃ 25℃ 25℃ 26℃
解:制作条形统计图或折线统计图如图.
(1)B市这周的平均气温高.
(2)A市这周的平均气温变化幅度大.
(3)A,B两市星期四的平均气温相差最大,相差7℃.
(4)A,B两市星期一和星期日的平均气温的差相同.
(5)B市的气温较稳定.
1.为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少?”,共有4个选项:
(A)1.5小时以上 (B)1~1.5小时 (C)0.5—1小时 (D)0.5小时以下
图①、②是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
(1)本次一共调查了%// //%名学生;
(2)在图①中将选项B的部分补充完整;
(3)若该校有3000名学生,请你估计
全校平均每天参加体育活动的时间
在0.5小时以下的学生可能有多少名?
解:(1)本次调查活动采取了抽样调查方式;
由图知A类有60人,占30%,则本次一共调查了60÷30%=200人;
200
(2)选B的人数:200×50%=100(人),
选项B的部分补充如图所示:
(3)3000×5%=150(人),
答:估计全校可能有150名学生平均每天参加体育活动的时间在0.5小时以下.
2.保障房建设是民心工程.某市从2008年开始加快保障房建设进程.现统计了该市2008年到2012年这5年新建保障房情况,绘制成如图所示的折线统计图和不完整的条形统计图.
(1)小丽看了统计图后说:“该市2011年新建保障房的套数比2010年少了.”你认为小丽的说法正确吗?请说明理由;
(2)请补全条形统计图;
(3)求这5年平均每年
新建保障房的套数.
解:(1)该市2011年新建保障房的增长率比2010年的增长率减少了,
但是保障房的总数在增加,故小丽的说法错误;
(2)2011年保障房的套数为:
750×(1+20%)=900(套),
设2008年保障房的套数为x,
所以x(1+20%)=600,则x=500,
如图所示:
(3)这5年平均每年新建保障房的套数为:
(500+600+750+900+1170)÷5=784(套),
答:这5年平均每年新建保障房的套数为784套.
3. 2013年3月28日是全国中小学生安全教育日,某校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计.请根据尚未完成的频率分布表和频数分布直方图(如图),解答下列问题:
频率分布表 分数段 频数 频率
50.5~60.5 16 0.08
60.5~70.5 40 0.2
70.5~80.5 50 0.25
80.5~90.5 m 0.35
90.5~100.5 24 n
(1)这次抽取了%////%名学生的竞赛成绩进行统计,
其中:m=%////%,n=%////%;
(2)补全频数分布直方图;
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?
解:(1)抽取的学生数:
16÷0.08=200(名),
m=200-16-40-50-24=70,
n=24÷200=0.12=12%;
(2)如图所示:
(3)1500×=420(人),
答:该校安全意识不强的学生约有420人.
4.(★)甲乙两种酒近几年的销售量和价格如下:
甲品牌酒的产量和价格:
乙品牌酒的产量和价格:
2002年 2006年 2010年
年度销售量(万瓶) 150 180 210
该年度的单价(元) 40 50 60
2006年 2008年 2010年
年度销售量(万瓶) 160 180 200
该年度的单价(元) 40 50 60
有人根据上面的图表,在下图中作出甲乙两种酒的价格变化的折线统计图:
(1)你认为哪一种酒的价格增长较快?为什么?这与上面画出的折线统计图,给你的感觉一致吗?为什么图象会给人这样的感觉?
(2)甲种酒的销售人员将甲种酒的销售信息制作成了如图③的条形统计图:请你在图④中作出甲种酒的年度销售量的条形统计图:
(3)两幅条形统计图给你的感觉一样吗?在甲种酒销售人员画的条形统计图中,2010年甲种酒的年度销售量看上去是2002年的多少倍?实际上呢?
(4)为了较直观地比较某两个统计量的变化速度,绘制折线统计图时,应注意什么?为了较直观地反映几个统计量之间的比例关系,绘制条形统计图时,应注意些什么?
解:(1)甲种酒是从2002年到2010年涨了20元,而乙种酒却是从2006年到2010年涨了20元,显然乙钟酒价格涨得比较快.但是从折线统计图看,似乎甲种酒价格涨得较快.这是因为图①与图②中坐标轴上同一单位长度所表示的意义不一致,图①与图②相比.纵轴(价格)被“拉长”了,横轴(年份)被“压缩”了,结果使得图①中的折线看起来更“陡”了.
(2)如图所示:
(3)图③与图④给人的感觉不一样,在图③中,2010年的销售量看上去是2002年的3倍左右;但根据统计表提供的数据信息,甲种酒2010年的销售量是2002年的1.4倍.人们往往习惯于根据条形统计图中的“柱”的高度来判断相应数值的大小,而图③的纵轴不是从“0”开始的(下面一段被砍掉了),因此“柱”的高度与其相应的数值不成正比,从而给人造成错觉.
(4)若要较为直观地比较两个统计量的变化速度,在绘制折线统计图时,应注意:两个图横轴上同一单位长度所表示的意义应一致,纵轴上同一单位长度所表示的意义也应一致.为了直观地反映几个统计量之间的比例关系,绘制条形统计图时应注意:纵轴上的数值应从0开始.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
