【五环分层导学-课件】6-6 单元复习 数据的收集与整理-北师大版数学七(上)
文档属性
| 名称 | 【五环分层导学-课件】6-6 单元复习 数据的收集与整理-北师大版数学七(上) |

|
|
| 格式 | pptx | ||
| 文件大小 | 20.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-02 00:00:00 | ||
图片预览











文档简介
(共34张PPT)
第六章 数据的收集与整理
单元复习
北师大版七年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
资料简介
【问题1】说一说可以运用哪些方法获得数据?
【问题2】抽样调查时,如何保证样本的代表性?举例说明.
【问题3】说一说怎样制作扇形统计图和频数直方图?
【问题4】条形统计图、折线统计图、扇形统计图、频数直方图各有什么特点?
【问题5】统计图有时可能会使人产生“错觉”,请举例说明.为了直观地反映数据信息,制作有关统计图时应注意些什么?
【问题6】梳理本章内容,用适当的方式(可以用表格、思维导图、列要点)呈现全章知识结构.
考点1:收集数据
【例题1】下列调查方式,你认为最合适的是(%////%)
A.了解北京市每天的流动人口数,采用抽样调查方式
B.旅客上飞机前的安检,采用抽样调查方式
C.了解北京市居民“一带一路”期间的出行方式,采用全面调查方式
D.日光灯管厂要检测一批灯管的使用寿命,采用全面调查方式
A
【例题2】2018年我市有近3万名学生参加中考,为了解这些考生的数学成绩,从中抽取1000名考生的数学成绩进行统计分析,以下说法正确的是(%////%)
A.近3万名考生是总体
B.这1000名考生是总体的一个样本
C.每位考生的数学成绩是个体
D.1000名学生是样本容量
C
考点2:整理与表示数据
【例题1】如图是某市电视台记者为了解市民获取新闻的主要途径,通过抽样调查绘制的一个条形统计图.若该市约有230万人,则可估计其中将报纸和手机上网作为获取新闻的主要途径的总人数大约为%// //%万人.
151.8
【例题2】近年来国内生产总值年增长率的变化情况如图,从图上看,下列结论中不正确的是(%////%)
A.1995~1999年,国内生
产总值的年增长率逐年减小
B.2000年国内生产总值的
年增长率开始回升
C.这7年中,每年的国内生
产总值不断增长
D.这7年中,每年的国内生
产总值有增有减
D
【例题3】如图,某校根据学生上学方式的一次抽样调查结果,绘制出一个未完成的扇形统计图,若该校共有学生1000人,则根据此估计步行上学的有%// //%人.
400
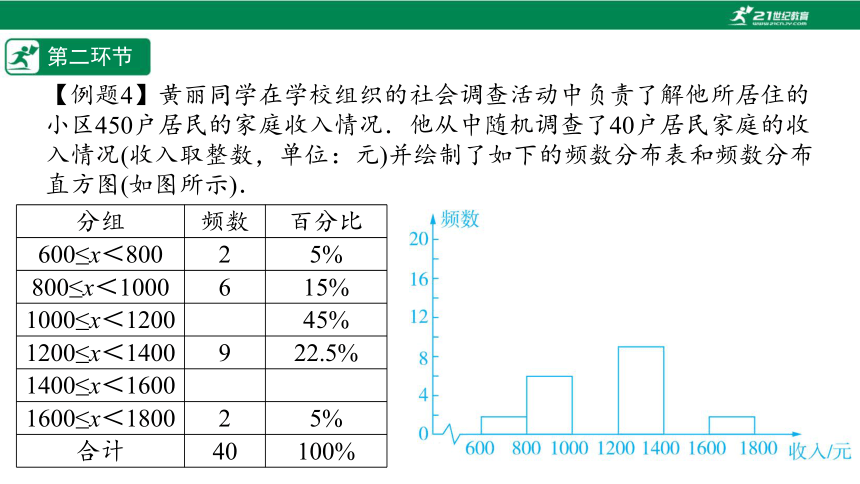
【例题4】黄丽同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况.他从中随机调查了40户居民家庭的收入情况(收入取整数,单位:元)并绘制了如下的频数分布表和频数分布直方图(如图所示).
分组 频数 百分比
600≤x<800 2 5%
800≤x<1000 6 15%
1000≤x<1200 45%
1200≤x<1400 9 22.5%
1400≤x<1600
1600≤x<1800 2 5%
合计 40 100%
根据以上提供的信息,解答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)请你估计该居民小区家庭属于中等收入(大于或等于1000不足1600元)的大约有多少户?
解:(1)收入是1000≤x<1200一组的户数是:
40×45%=18(户),
1400≤x<1600一组的户数是:
40-(2+6+18+9+2)=3,
所占百分比为×100%=7.5%.
(2)依次填写为18,3,7 % :
(3)估计该居民小区家庭属于中等收入(大于1000不足
1600元)的大约有450×(45%+22.5%+7.5%)≈338(户).
易错点1:调查对象理解有误
1.为了了解某校初三年级400名学生的体重情况,从中抽查了50名学生的体重进行统计分析,在这个问题中,总体是(%////%)
A.400名学生的体重 B.被抽取的50名学生
C.400名学生 D.被抽取的50名学生的体重
A
易错点2:扇形统计图中百分比理解有误
2.甲、乙两所学校男女生人数可见如图统计图,甲学校有1000人,乙学校有1250人,则(%////%)
A.甲校的女生与乙校的女生一样多
B.甲校的女生比乙校的女生少
C.甲校的女生比乙校的女生多
D.甲校与乙校共有女生1250人
B
1.(3分)今年我市有4万名学生参加中考,为了了解这些考生的数学成绩,从中抽取2000名考生的数学成绩进行统计分析.在这个问题中,下列说法:①这4万名考生的数学中考成绩的全体是总体;②每个考生是个体;③2000名考生是总体的一个样本;④样本容量是2000.其中说法正确的有(%////%)
A.4个 B.3个 C.2个 D.1个
C
2.(3分)下列调查中,最适合采用全面调查(普查)方式的是(%////%)
A.对重庆市辖区内长江流域水质情况的调查
B.对乘坐飞机的旅客是否携带违禁物品的调查
C.对一个社区每天丢弃塑料袋数量的调查
D.对重庆电视台“天天630”栏目收视率的调查
B
3.(3分)在选取样本时,下列说法不正确的是(%////%)
A.所选样本必须足够大
B.所选样本要具有普遍代表性
C.所选样本可按自己的爱好抽取
D.仅仅增加调查人数不一定能提高调查质量
C
4.(3分)以下问题不适合全面调查的是(%////%)
A.调查某班学生每周课前预习的时间
B.调查某中学在职教师的身体健康状况
C.调查全国中小学生课外阅读情况
D.调查某校篮球队员的身高
C
5.(3分)某校七(1)班全体同学喜欢的球类运动如图所示的统计图表示,下面说法正确的是(%////%)
A.从图中可以直接看出喜欢各种球类的具体人数
B.从图中可以直接看出全班的总人数
C.从图中可以直接看出全班同学一学期来喜欢各种球类的变化情况
D.从图中可以直接看出全班同学现在最喜欢各种球类人数的百分比
D
6.(3分)如图是某班45名同学爱心捐款额的频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一组是(%////%)
A.5~10元 B.10~15元
C.15~20元 D.20~25元
C
7.(3分)对于条形统计图、折线统计图和扇形统计图这三种常见的统计图,下列说法正确的是(%////%)
A.通常不可互相转换
B.条形统计图能清楚地反映事物的变化情况
C.折线统计图能清楚地表示出每个项目的具体数目
D.扇形统计图能清楚地表示出各部分在总体中所占的百分比
D
8.(3分)某校公布了该校反映各年级学生体育达标情况的两张统计图(如图所示),该校七、八、九三个年级共有学生800人.甲,乙,丙三个同学看了这两张统计图后,甲说:“七年级的体育达标率最高.”乙说:“八年级共有学生264人.”丙说:“九年级的体育达标率最高.”甲,乙,丙三个同学中,说法正确的是(%////%)
A.甲和乙
B.乙和丙
C.甲和丙
D.甲和乙及丙
B
9.(3分)对某校初三的480名学生的身高情况进行考察,从中抽取100名学生的身高,则这个问题中的样本为%// //%.
100名学生的身高
10.(3分)某学校计划购买一批课外读物,为了了解学生对课外读物的需求情况,学校进行了一次“我最喜爱的课外读物”的调查,设置了“文学”、“科普”、“艺术”和“其他”四个类别,规定每人必须并且只能选择其中一类,现从全体学生的调查表中随机抽取了部分学生的调查表进行统计,并把统计结果绘制了如图所示的两幅不完整的统计图,则在扇形统计图中,艺术类读物所在扇形的圆心角是%////%.
72°
11.(4分)某学校要了解学生上学交通情况,选取九年级全体学生进行调查,根据调查结果,画出扇形统计图(如图所示),图中“公交车”对应的扇形圆心角为60°,“自行车”对应的扇形圆心角为120°,已知九年级乘公交车上学的人数为50人.
(1)九年级学生中,骑自行车和乘公交
车上学哪个更多?多多少人?
(2)如果全校有学生2000人,学校准备
的400个自行车停车位是否足够?
解:(1)乘公交车所占的百分比,
调查的样本容量50300人,
骑自行车的人数300×100人,
骑自行车的人数多,多100-50=50人;
(2)全校骑自行车的人数2000×≈667人,
667>400,
故学校准备的400个自行车停车位不足够.
12.(6分)小明家2019年的四个季度的用电量如下:
其中各种电器用电量如下表:
季度名称 用电量(单位:度)
第一季度 250
第二季度 150
第三季度 400
第四季度 200
各种电器 用电量(单位:度)
空调 250
冰箱 100
彩电 150
其他 100
小明根据上面的数据制成如图的统计图.
根据以上三幅统计图回答.
(1)从哪幅统计图可以看出各种季度用电量变化情况?
(2)从哪幅统计图中可以看出冰箱用电量超过总用电量的.
(3)从哪幅统计图中可以清楚地看出空调的用电量?
/解:(1)各种季度用电量变化情况就是要知道事物的变化情况,所以从折线统计图可以看出;
(2)冰箱用电量超过总用电量的就是要知道部分占总体的百分比大小,所以从扇形统计图可以看出;
(3)空调的用电量就是要知道项目的数据,所以从条形统计图可以看出.
13.(6分)某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).
请你根据图中所给的信息解答下列问题:
(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有%////%人达标;
(3)若该校学生有学生2000
人,请你估计此次测试中,
全校达标的学生有多少人?
解:(1)根据题意得:24÷20%=120(人),
则“优秀”人数为120-(24+36)=60(人),
“一般”占的百分比为×100%=30%,
补全统计图,如图所示:
(2)根据题意得:36+60=96(人),
则达标的人数为96人;
(3)根据题意得:×2000=1600(人),
则全校达标的学生有1600人.
14.(4分)为了治理大气污染,我国中部某市抽取了该市2014年中120天的空气质量指数,绘制了如下不完整的统计图表:
空气质量指数统计表 级别 指数 天数 百分比
优 0~50 24 m
良 51~100 a 40%
轻度污染 101~150 18 15%
中度污染 151~200 15 12.5%
重度污染 201~300 9 7.5%
严重污染 大于300 6 5%
合计 120 100%
请根据图表中提供的信息,解答下面的问题:
(1)空气质量指数统计表中的a=%////%,m=%// //%;
(2)请把如图所示空气质量指数条形统计图补充完整:
(3)若绘制“空气质量指数扇形统计图”,级别为“优”所对应扇形的圆心角是%////%;
(4)估计该市2014年(365天)中空气质量指数大于100的天数约有%////%天.
解:(1)a=120×40%=48,m=24÷120=20%.
故答案为:48,20%;
48
20%
(2)如图所示:
(3)360°×20%=72°.
故答案为:72;
(4)365×146(天).
故答案为:146.
第六章 数据的收集与整理
单元复习
北师大版七年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
资料简介
【问题1】说一说可以运用哪些方法获得数据?
【问题2】抽样调查时,如何保证样本的代表性?举例说明.
【问题3】说一说怎样制作扇形统计图和频数直方图?
【问题4】条形统计图、折线统计图、扇形统计图、频数直方图各有什么特点?
【问题5】统计图有时可能会使人产生“错觉”,请举例说明.为了直观地反映数据信息,制作有关统计图时应注意些什么?
【问题6】梳理本章内容,用适当的方式(可以用表格、思维导图、列要点)呈现全章知识结构.
考点1:收集数据
【例题1】下列调查方式,你认为最合适的是(%////%)
A.了解北京市每天的流动人口数,采用抽样调查方式
B.旅客上飞机前的安检,采用抽样调查方式
C.了解北京市居民“一带一路”期间的出行方式,采用全面调查方式
D.日光灯管厂要检测一批灯管的使用寿命,采用全面调查方式
A
【例题2】2018年我市有近3万名学生参加中考,为了解这些考生的数学成绩,从中抽取1000名考生的数学成绩进行统计分析,以下说法正确的是(%////%)
A.近3万名考生是总体
B.这1000名考生是总体的一个样本
C.每位考生的数学成绩是个体
D.1000名学生是样本容量
C
考点2:整理与表示数据
【例题1】如图是某市电视台记者为了解市民获取新闻的主要途径,通过抽样调查绘制的一个条形统计图.若该市约有230万人,则可估计其中将报纸和手机上网作为获取新闻的主要途径的总人数大约为%// //%万人.
151.8
【例题2】近年来国内生产总值年增长率的变化情况如图,从图上看,下列结论中不正确的是(%////%)
A.1995~1999年,国内生
产总值的年增长率逐年减小
B.2000年国内生产总值的
年增长率开始回升
C.这7年中,每年的国内生
产总值不断增长
D.这7年中,每年的国内生
产总值有增有减
D
【例题3】如图,某校根据学生上学方式的一次抽样调查结果,绘制出一个未完成的扇形统计图,若该校共有学生1000人,则根据此估计步行上学的有%// //%人.
400
【例题4】黄丽同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况.他从中随机调查了40户居民家庭的收入情况(收入取整数,单位:元)并绘制了如下的频数分布表和频数分布直方图(如图所示).
分组 频数 百分比
600≤x<800 2 5%
800≤x<1000 6 15%
1000≤x<1200 45%
1200≤x<1400 9 22.5%
1400≤x<1600
1600≤x<1800 2 5%
合计 40 100%
根据以上提供的信息,解答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)请你估计该居民小区家庭属于中等收入(大于或等于1000不足1600元)的大约有多少户?
解:(1)收入是1000≤x<1200一组的户数是:
40×45%=18(户),
1400≤x<1600一组的户数是:
40-(2+6+18+9+2)=3,
所占百分比为×100%=7.5%.
(2)依次填写为18,3,7 % :
(3)估计该居民小区家庭属于中等收入(大于1000不足
1600元)的大约有450×(45%+22.5%+7.5%)≈338(户).
易错点1:调查对象理解有误
1.为了了解某校初三年级400名学生的体重情况,从中抽查了50名学生的体重进行统计分析,在这个问题中,总体是(%////%)
A.400名学生的体重 B.被抽取的50名学生
C.400名学生 D.被抽取的50名学生的体重
A
易错点2:扇形统计图中百分比理解有误
2.甲、乙两所学校男女生人数可见如图统计图,甲学校有1000人,乙学校有1250人,则(%////%)
A.甲校的女生与乙校的女生一样多
B.甲校的女生比乙校的女生少
C.甲校的女生比乙校的女生多
D.甲校与乙校共有女生1250人
B
1.(3分)今年我市有4万名学生参加中考,为了了解这些考生的数学成绩,从中抽取2000名考生的数学成绩进行统计分析.在这个问题中,下列说法:①这4万名考生的数学中考成绩的全体是总体;②每个考生是个体;③2000名考生是总体的一个样本;④样本容量是2000.其中说法正确的有(%////%)
A.4个 B.3个 C.2个 D.1个
C
2.(3分)下列调查中,最适合采用全面调查(普查)方式的是(%////%)
A.对重庆市辖区内长江流域水质情况的调查
B.对乘坐飞机的旅客是否携带违禁物品的调查
C.对一个社区每天丢弃塑料袋数量的调查
D.对重庆电视台“天天630”栏目收视率的调查
B
3.(3分)在选取样本时,下列说法不正确的是(%////%)
A.所选样本必须足够大
B.所选样本要具有普遍代表性
C.所选样本可按自己的爱好抽取
D.仅仅增加调查人数不一定能提高调查质量
C
4.(3分)以下问题不适合全面调查的是(%////%)
A.调查某班学生每周课前预习的时间
B.调查某中学在职教师的身体健康状况
C.调查全国中小学生课外阅读情况
D.调查某校篮球队员的身高
C
5.(3分)某校七(1)班全体同学喜欢的球类运动如图所示的统计图表示,下面说法正确的是(%////%)
A.从图中可以直接看出喜欢各种球类的具体人数
B.从图中可以直接看出全班的总人数
C.从图中可以直接看出全班同学一学期来喜欢各种球类的变化情况
D.从图中可以直接看出全班同学现在最喜欢各种球类人数的百分比
D
6.(3分)如图是某班45名同学爱心捐款额的频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一组是(%////%)
A.5~10元 B.10~15元
C.15~20元 D.20~25元
C
7.(3分)对于条形统计图、折线统计图和扇形统计图这三种常见的统计图,下列说法正确的是(%////%)
A.通常不可互相转换
B.条形统计图能清楚地反映事物的变化情况
C.折线统计图能清楚地表示出每个项目的具体数目
D.扇形统计图能清楚地表示出各部分在总体中所占的百分比
D
8.(3分)某校公布了该校反映各年级学生体育达标情况的两张统计图(如图所示),该校七、八、九三个年级共有学生800人.甲,乙,丙三个同学看了这两张统计图后,甲说:“七年级的体育达标率最高.”乙说:“八年级共有学生264人.”丙说:“九年级的体育达标率最高.”甲,乙,丙三个同学中,说法正确的是(%////%)
A.甲和乙
B.乙和丙
C.甲和丙
D.甲和乙及丙
B
9.(3分)对某校初三的480名学生的身高情况进行考察,从中抽取100名学生的身高,则这个问题中的样本为%// //%.
100名学生的身高
10.(3分)某学校计划购买一批课外读物,为了了解学生对课外读物的需求情况,学校进行了一次“我最喜爱的课外读物”的调查,设置了“文学”、“科普”、“艺术”和“其他”四个类别,规定每人必须并且只能选择其中一类,现从全体学生的调查表中随机抽取了部分学生的调查表进行统计,并把统计结果绘制了如图所示的两幅不完整的统计图,则在扇形统计图中,艺术类读物所在扇形的圆心角是%////%.
72°
11.(4分)某学校要了解学生上学交通情况,选取九年级全体学生进行调查,根据调查结果,画出扇形统计图(如图所示),图中“公交车”对应的扇形圆心角为60°,“自行车”对应的扇形圆心角为120°,已知九年级乘公交车上学的人数为50人.
(1)九年级学生中,骑自行车和乘公交
车上学哪个更多?多多少人?
(2)如果全校有学生2000人,学校准备
的400个自行车停车位是否足够?
解:(1)乘公交车所占的百分比,
调查的样本容量50300人,
骑自行车的人数300×100人,
骑自行车的人数多,多100-50=50人;
(2)全校骑自行车的人数2000×≈667人,
667>400,
故学校准备的400个自行车停车位不足够.
12.(6分)小明家2019年的四个季度的用电量如下:
其中各种电器用电量如下表:
季度名称 用电量(单位:度)
第一季度 250
第二季度 150
第三季度 400
第四季度 200
各种电器 用电量(单位:度)
空调 250
冰箱 100
彩电 150
其他 100
小明根据上面的数据制成如图的统计图.
根据以上三幅统计图回答.
(1)从哪幅统计图可以看出各种季度用电量变化情况?
(2)从哪幅统计图中可以看出冰箱用电量超过总用电量的.
(3)从哪幅统计图中可以清楚地看出空调的用电量?
/解:(1)各种季度用电量变化情况就是要知道事物的变化情况,所以从折线统计图可以看出;
(2)冰箱用电量超过总用电量的就是要知道部分占总体的百分比大小,所以从扇形统计图可以看出;
(3)空调的用电量就是要知道项目的数据,所以从条形统计图可以看出.
13.(6分)某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).
请你根据图中所给的信息解答下列问题:
(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有%////%人达标;
(3)若该校学生有学生2000
人,请你估计此次测试中,
全校达标的学生有多少人?
解:(1)根据题意得:24÷20%=120(人),
则“优秀”人数为120-(24+36)=60(人),
“一般”占的百分比为×100%=30%,
补全统计图,如图所示:
(2)根据题意得:36+60=96(人),
则达标的人数为96人;
(3)根据题意得:×2000=1600(人),
则全校达标的学生有1600人.
14.(4分)为了治理大气污染,我国中部某市抽取了该市2014年中120天的空气质量指数,绘制了如下不完整的统计图表:
空气质量指数统计表 级别 指数 天数 百分比
优 0~50 24 m
良 51~100 a 40%
轻度污染 101~150 18 15%
中度污染 151~200 15 12.5%
重度污染 201~300 9 7.5%
严重污染 大于300 6 5%
合计 120 100%
请根据图表中提供的信息,解答下面的问题:
(1)空气质量指数统计表中的a=%////%,m=%// //%;
(2)请把如图所示空气质量指数条形统计图补充完整:
(3)若绘制“空气质量指数扇形统计图”,级别为“优”所对应扇形的圆心角是%////%;
(4)估计该市2014年(365天)中空气质量指数大于100的天数约有%////%天.
解:(1)a=120×40%=48,m=24÷120=20%.
故答案为:48,20%;
48
20%
(2)如图所示:
(3)360°×20%=72°.
故答案为:72;
(4)365×146(天).
故答案为:146.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
