2024云南中考数学二轮专题复习 题型六 二次函数与几何综合题课件 76张PPT
文档属性
| 名称 | 2024云南中考数学二轮专题复习 题型六 二次函数与几何综合题课件 76张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-02 16:48:25 | ||
图片预览



文档简介
(共76张PPT)
题型六 二次函数与几何综合题
类型一~类型二
类型三 与三角形形状有关的问题
函数微技能—画图确定动点位置
一阶
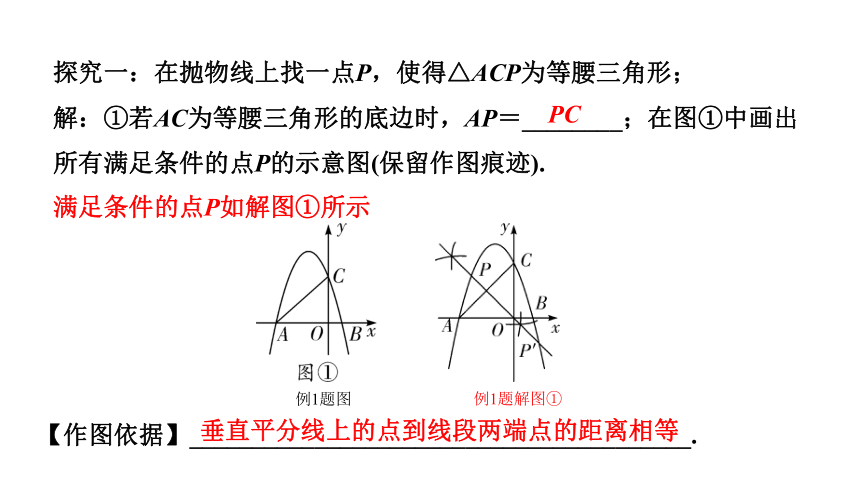
例1. 如图,已知抛物线交x轴于A、B两点(点A在点B左侧),与y轴交于点C,连接AC.
例1题图
探究一:在抛物线上找一点P,使得△ACP为等腰三角形;
解:①若AC为等腰三角形的底边时,AP=________;在图①中画出所有满足条件的点P的示意图(保留作图痕迹).
【作图依据】________________________________________.
PC
满足条件的点P如解图①所示
例1题解图①
垂直平分线上的点到线段两端点的距离相等
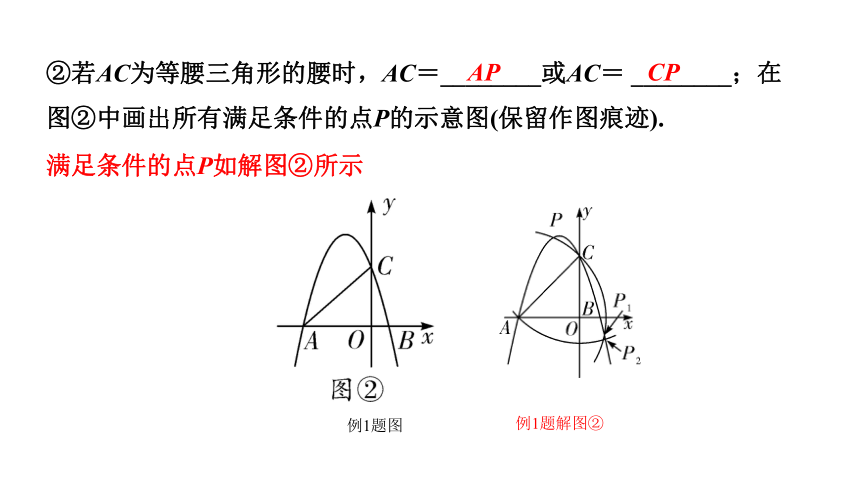
例1题图
②若AC为等腰三角形的腰时,AC=________或AC= ________;在图②中画出所有满足条件的点P的示意图(保留作图痕迹).
AP
CP
满足条件的点P如解图②所示
例1题图
例1题解图②
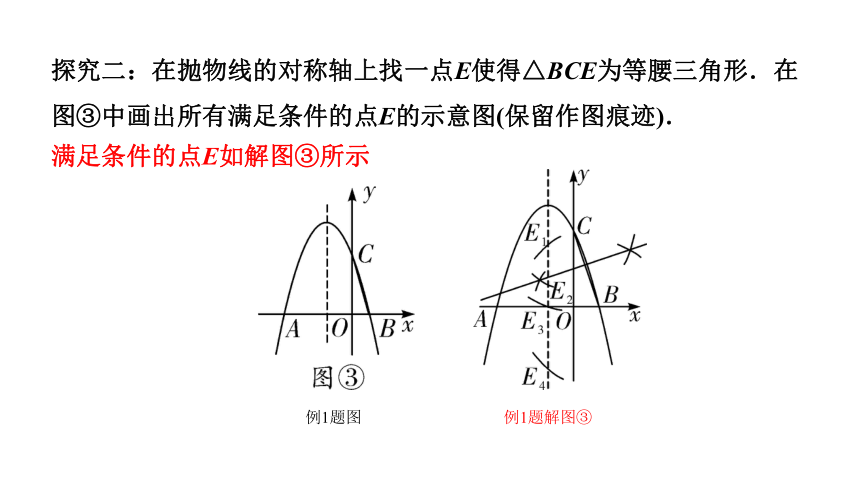
探究二:在抛物线的对称轴上找一点E使得△BCE为等腰三角形.在图③中画出所有满足条件的点E的示意图(保留作图痕迹).
例1题图
满足条件的点E如解图③所示
例1题解图③
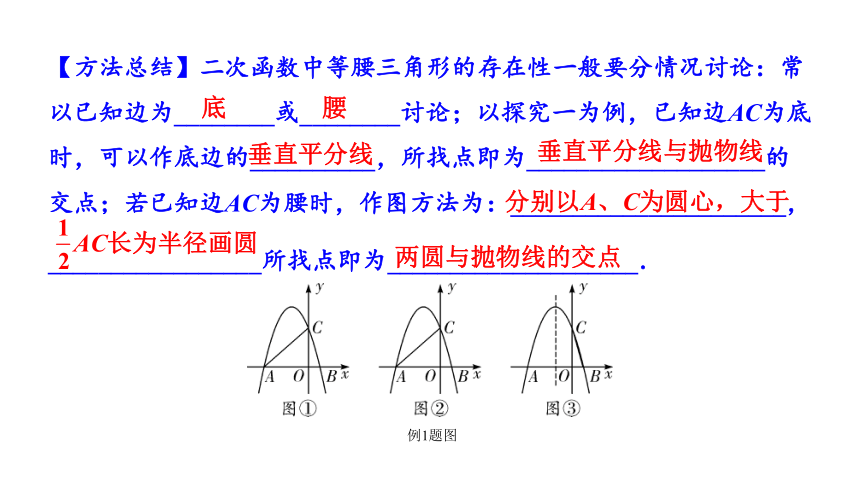
【方法总结】二次函数中等腰三角形的存在性一般要分情况讨论:常以已知边为________或________讨论;以探究一为例,已知边AC为底时,可以作底边的__________,所找点即为___________________的交点;若已知边AC为腰时,作图方法为:______________________,
_________________所找点即为____________________.
例1题图
底
腰
垂直平分线
垂直平分线与抛物线
分别以A、C为圆心,大于
AC长为半径画圆
两圆与抛物线的交点
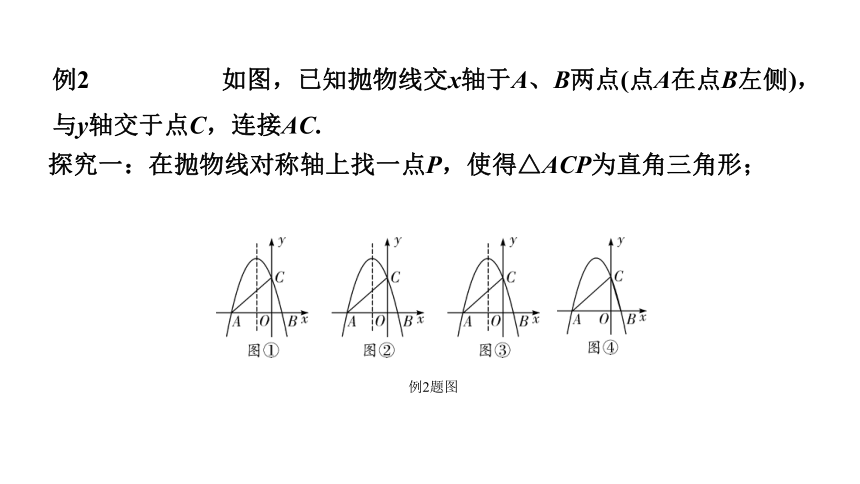
例2 如图,已知抛物线交x轴于A、B两点(点A在点B左侧),与y轴交于点C,连接AC.
例2题图
探究一:在抛物线对称轴上找一点P,使得△ACP为直角三角形;
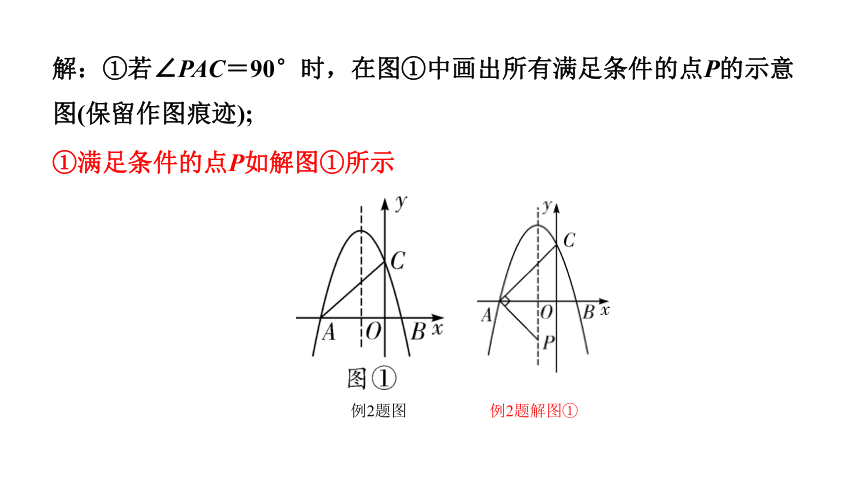
解:①若∠PAC=90°时,在图①中画出所有满足条件的点P的示意图(保留作图痕迹);
例2题图
①满足条件的点P如解图①所示
例2题解图①
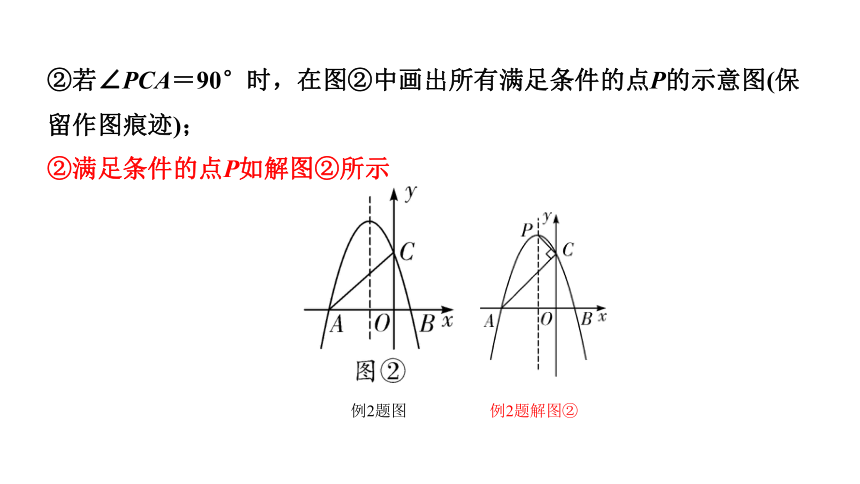
②若∠PCA=90°时,在图②中画出所有满足条件的点P的示意图(保留作图痕迹);
②满足条件的点P如解图②所示
例2题图
例2题解图②
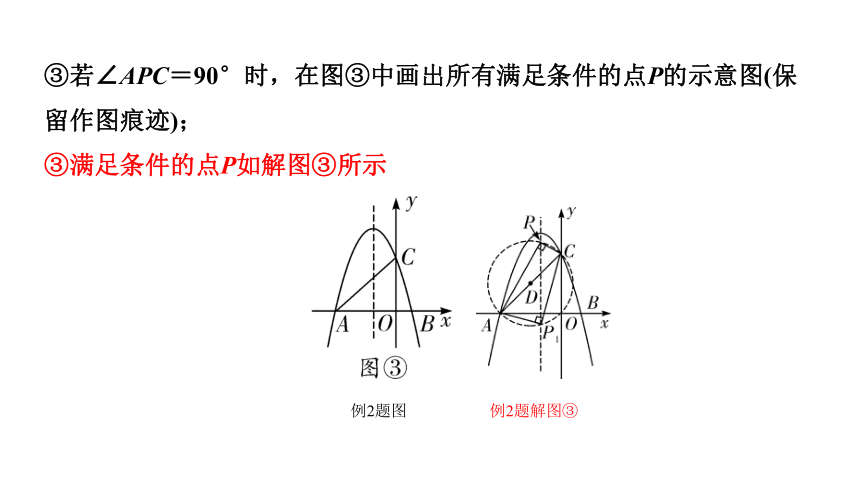
③若∠APC=90°时,在图③中画出所有满足条件的点P的示意图(保留作图痕迹);
③满足条件的点P如解图③所示
例2题图
例2题解图③
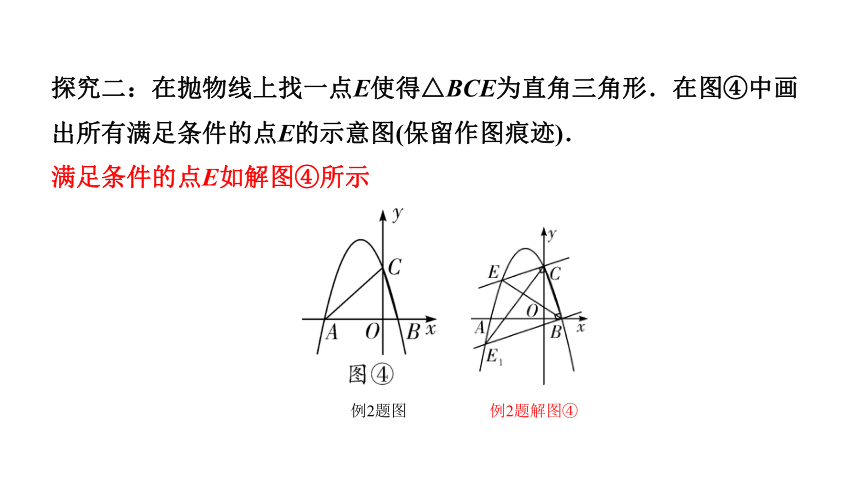
探究二:在抛物线上找一点E使得△BCE为直角三角形.在图④中画出所有满足条件的点E的示意图(保留作图痕迹).
满足条件的点E如解图④所示
例2题图
例2题解图④
【方法总结】二次函数中直角三角形的存在性一般要分情况讨论;以探究一为例,若∠PAC=90°,过点A作PA⊥AC交抛物线对称轴于点P;若∠PCA=90°,作图方法:__________________________________,所找点为_________________;若∠APC=90°,作图方法:________
___________________________,所找点为____________________.
过点C作PC⊥AC交抛物线对称轴于点P
PC与对称轴的交点
点D为圆心,AC长为直径作圆
以AC的中
对称轴与⊙D的交点
设问突破
二阶
一题多设问
例3 已知抛物线的解析式为y=-x2+2x+3,与x轴交于点A、B,与y轴交于点C,抛物线的顶点为D,对称轴DF交BC于点E,交x轴于点F.
(1)如图①,在抛物线上是否存在一点G,使得△BCG是以BC为底边的等腰三角形?若存在,求出点G的坐标;若不存在,请说明理由;
例3题图①
【思维引导】要使△BCG是以BC为底的等腰三角形,可作BC的垂直平分线,其与抛物线的交点即为所求点G.
例3题图①
解:(1)存在.
令抛物线中y=0,解得x=-1或x=3,
∴A(-1,0),B(3,0).
令抛物线中x=0,则y=3,∴C(0,3).
∴直线BC的解析式为y=-x+3,
线段BC的中点坐标为( , ),
∴易得BC的垂直平分线l的解析式为y=x,
联立抛物线与直线l的解析式可得
解得 或
∴满足条件的点G的坐标为( , )
或( , );
例3题图①
(2)如图②,在抛物线对称轴上是否存在一点M,使得△BCM是等腰三角形?若存在,求出点M的坐标,若不存在,请说明理由;
例3题图②
【思维引导】设点M坐标,然后表示出BM和CM,分BC为腰,BC为底边两种情况讨论,列方程,若方程有解,则存在,否则不存在.
(2)存在.
设点M(1,m),
由题意得BC=3 ,BM= ,
CM= ,
例3题图②
①当BC为腰时,
a.若BC=BM,即3 = ,
解得m=± ,则M1(1, ),M2(1,- );
b.若BC=CM,即3 = ,
解得m=3± ,则M3(1,3+ ),M4(1,3- );
②当BC为底边时,则CM=BM,
即 = ,
解得m=1,则M5(1,1).
例3题图②
综上所述,满足条件的点M的坐标为
(1, )或(1,- )或(1,3+ )或(1,3- )或(1,1);
(3)如图③,在抛物线的对称轴上是否存在一点H,使得△BCH是直角三角形?若存在,求出点H的坐标,若不存在,请说明理由;
例3题图③
【思维引导】分∠HCB=90°、∠HBC=90°、∠CHB=90°三种情况讨论,利用直角三角形的性质求解.
(3)存在.
设点H的坐标为(1,h),要使△BCH为直角三角形,需分三种情况讨论:
①当∠HCB=90°时,如解图①,
例3题解图①
∵点D为抛物线顶点,∴D(1,4),
∵CD2=12+(4-3)2=2,
BD2=(3-1)2+42=20,
BC2=32+32=18.
∴BC2+CD2=BD2.
∴∠DCB=90°.
∴当点H与点D重合时,∠BCH=90°,此时点H的坐标为(1,4);
例3题解图①
②当∠HBC=90°时,如解图②,
例3题解图②
∵OB=OC=3,
∴∠BCO=45°.
∴∠BEH=∠BCO=45°.
∴BE=BH.
∵EH⊥BF,
∴FH=BF=OB-OF=2.
∴此时点H的坐标为(1,-2);
③当∠CHB=90°时,如解图③,
设点H(1,h),过点C作CM⊥DF于点M,∴M(1,3),
∵∠CHM+∠BHE=90°,∠BHE+∠HBF=90°,
∴∠CHM=∠HBF,
又∵∠CMH=∠HFB=90°,∴△CHM∽△HBF,
∴ = ,即 = ,
解得h1= ,h2= ,
∴此时点H有两个,坐标分别为(1, )或(1, );
综上所述,点H的坐标为(1,4)或(1,-2)或(1, )或(1, );
例3题解图③
(4)如图④,在抛物线上是否存在一点N,使得△BCN是以BC为直角边的直角三角形?若存在,求出点N的坐标,若不存在,请说明理由.
【思维引导】△BCN是以BC为直角边的直角三角形,需分点B和点C分别为直角顶点两种情况讨论,结合△OBC是等腰直角三角形,利用等腰直角三角形的性质求解.
例3题图④
(4)存在.
设N(n,-n2+2n+3),分两种情况讨论;
①当∠NCB=90°时,如解图④,过点N作NG⊥y轴于点G,
G
(N)
∵OB=OC,
∴∠BCO=∠CBO=45°.
∴∠NCG=180°-∠BCO-∠BCD=45°.
∴CG=NG.
∵CG=OG-OC=-n2+2n+3-3=-n2+2n,NG=n,
∴-n2+2n=n.
解得n1=0(舍),n2=1.
∴N(1,4);
例3题图④
G
(N)
则∠HBN=90°-∠CBO=45°,
∴BH=NH.
∵BH=3-n,NH=-(-n2+2n+3)=n2-2n-3.
∴3-n=n2-2n-3,解得n1=3(舍),n2=-2.
∴N(-2,-5).
综上所述,点N的坐标为(1,4)或(-2,-5).
②当∠NBC=90°时,如解图⑤,过点N作NH⊥x轴于点H,
例3题解图⑤
类型四 与四边形形状有关的问题
函数微技能—画图确定动点位置
一阶
例1 如图,已知抛物线交x轴于A、B两点(点A在点B左侧),与y轴交于点C,连接AC.
例1题图
探究一:P是平面内一点,找出点P,使得以A、B、C、P为顶点的四边形为平行四边形;
解:①若AC为平行四边形的边时,AC∥BP,且AC=BP,在图①中画出所有满足条件的点P的示意图(保留作图痕迹).
例1题图
①满足条件的点P如解图①所示
例1题解图①
②若AC为平行四边形的对角线时,在图②中画出所有满足条件的点P的示意图(保留作图痕迹).
例1题图
②满足条件的点P如解图②所示
例1题解图②
讨论:探究菱形的存在性时,要区别于平行四边形的点为:①菱形各边相等;②菱形的对角线互相垂直.
探究二:M是x轴上的点,N是平面内一点,使得以B、C、M、N为顶点的四边形为菱形,在图③中画出满足条件的点M、N(保留作图痕迹).
例1题图
例1题解图③
满足条件的点M、N如解图③所示
【方法总结】二次函数中特殊四边形的存在性一般要分情况讨论:常以已知边为______或________讨论;以探究一为例,若AC为边时,过点B作BP∥AC,点P可在x轴上方,也可在x轴下方;作图依据:________________________________________;若AC为对角线时,作法:_________________________________________________.
边
对角线
一组对边平行且相等的四边形是平行四边形
取AC的中点D,连接BD并延长至点P,使得DP=BP
设问突破
二阶
一题多设问
例2 已知抛物线y=x2+6x+5与x轴交于A、B两点,与y轴交于点C,M为顶点,抛物线的对称轴l与x轴交于点D,与过A、C两点的直线交于点E.
(1)如图①,将抛物线沿x轴平移,使得点A落在点B处记为A′,此时点C的对应点为C′,求点C′的坐标,判断四边形AA′C′C的形状,并说明理由.
例2题图①
例2题图①
【思维引导】根据平移的性质可知,点A平移到点B的规律与点C平移到点C′的规律一致,即可得到点C′的坐标,再由AA′=CC′,AA′∥CC′即可判断四边形的形状.
(1)四边形AA′C′C是平行四边形,理由如下:
∵抛物线y=x2+6x+5与x轴交于A、B两点,与y轴交于点C,
∴当x=0时,y=5;当y=0,即x2+6x+5=0时,
解得x=-1或-5,
∴A(-5,0)、B(-1,0)、C(0,5),
∴AB=-1-(-5)=4,
∴由平移的性质得C′(4,5),AA′=CC′,AA′∥CC′,
∴四边形AA′C′C是平行四边形;
例2题图①
(2)如图②,设点G是抛物线上一点,过点G作GH∥x轴交对称轴l于点H,是否存在点G,使得以A、B、G、H为顶点的四边形是平行四边形?若存在,求出点G的坐标;若不存在,请说明理由;
例2题图②
【思维引导】由GH∥x轴,AB在x轴上可知AB∥GH,从而只需GH=AB即可得到以A、B、G、H为顶点的四边形是平行四边形.分点H在点G左侧和点H在点G右侧两种情况.
例2题图②
(2)存在,
由(1)得点A的坐标是(-5,0),点B的坐标是(-1,0).
∵点G在抛物线上,则设点G的坐标为(g,g2+6g+5),
∵GH∥x轴,点H在对称轴l上,
对称轴为直线x=- =-3,
∴H(-3,g2+6g+5),
∵GH∥AB,
∴要使以A、B、G、H为顶点的四边形为平行四边形,
需GH=AB=4,
例2题图②
即|g+3|=4,解得g=1或g=-7.
当g=1时,g2+6g+5=12,
此时点G的坐标为G1(1,12);
当g=-7时,g2+6g+5=12,
此时点G的坐标为G2(-7,12).
综上所述,满足条件的点G有两个,坐标分别为
(1,12)或(-7,12);
(3)如图③,G是坐标平面内一点,当以A、C、G、M为顶点的四边形是平行四边形时,求点G的坐标;
例2题图③
【思维引导】已知平行四边形的三个顶点,求第四个顶点,可顺次连接已知三点构成△ACM,分别以AC,AM,CM作为平行四边形的对角线进行分类讨论,利用“对角线互相平分的四边形是平行四边形”及中点坐标公式求解.
例2题图③
(3)∵抛物线的解析式为y=x2+6x+5=(x+3)2-4,
∴点M(-3,-4).
设点G(x,y),
∵A(-5,0),C(0,5),
分三种情况讨论:
①若AC为平行四边形AMCG的对角线时,
则AC与MG互相平分,
∴ = , = ,
∴ = , = ,
解得
∴G1(-2,9);
例2题图③
②若AM为平行四边形AGMC的对角线,则AM与CG互相平分,
∴ = , = ,
∴ = , = ,
解得
∴G2(-8,-9);
例2题图③
③若CM为平行四边形AMGC的对角线,则AG与CM互相平分,
∴ = , = ,
∴ = , = ,
解得
∴G3(2,1).
综上所述,点G的坐标为(-2,9)或
(-8,-9)或(2,1);
例2题图③
(4)如图④,设G是抛物线的对称轴上一点,K是坐标平面内一点,是否存在点G,使得以A,C,G,K 为顶点的四边形是矩形?若存在,求出点G的坐标;若不存在,请说明理由;
例2题图④
【思维引导】要使以A,C,G,K为顶点的四边形是矩形,只需△ACG是直角三角形即可,可分为①∠ACG=90°,②∠CAG=90°,③∠CGA=90°三种情况,分别利用勾股定理列方程即可求解.
(4)存在.
要使以A,C,G,K为顶点的四边形是矩形,则△ACG一定是直角三角形.
∵点G在对称轴上,
∴设点G的坐标为(-3,g),
由勾股定理得AC2=52+52=50,
AG2=(-5+3)2+g2=4+g2,
CG2=32+(g-5)2=g2-10g+34,
分三种情况讨论:
例2题图④
①若∠ACG=90°,
则AC2+CG2=AG2,
即50+g2-10g+34=4+g2,解得g=8,
此时点G的坐标为(-3,8);
②若∠CAG=90°,
则AC2+AG2=CG2,
即50+4+g2=g2-10g+34,
解得g=-2,
此时点G的坐标为(-3,-2);
例2题图④
③若∠CGA=90°,
则CG2+AG2=AC2,
即g2-10g+34+4+g2=50,
解得g1=6,g2=-1,
此时点G的坐标为(-3,6)或
(-3,-1);
综上所述,存在满足题意的点G,点G的坐标为(-3,8)或(-3,-2)或(-3,6)或(-3,-1);
例2题图④
(5)如图⑤,设Q是抛物线上一点,点R是坐标平面内一点,是否存在四边形AQCR是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.
例2题图⑤
【思维引导】由四边形AQCR是菱形可确定AC是对角线,则Q、R均在AC的垂直平分线上,联立方程求解即可.
(5)存在.
如解图,过点O作OI⊥AC于点I,
I
Q1
Q2
∵四边形AQCR是菱形,∴QR垂直平分AC.
∵OA=OC=5,
∴AI=CI,
∴OI是AC的垂直平分线,
∴点Q、R在AC的垂直平分线上,
∴点Q是直线OI与抛物线的交点.
∵I是AC的中点,
∴xI= =- ,yI= = ,
∴点I的坐标为(- , ),
例2题图⑤
I
Q1
Q2
例2题图⑤
I
Q1
Q2
设直线OI的解析式为y=tx,将点I的坐标代入,可得t=-1,
∴直线OI的解析式为y=-x,
联立
解得 或
∴存在满足题意的点Q,
点Q的坐标为( , )或( , ).
类型五 与三角形相似有关的问题
函数微技能—画图确定动点位置
一阶
例1 如图,已知抛物线交x轴于A、B两点(点A在点B左侧),与y轴交于点C,连接AC.
例1题图
探究一:P是线段AC上一点,找出点P,使得以A、O、P为顶点的三角形与△ABC相似;
解:①若△AOP∽△ABC时,在图①中画出所有满足条件的点P的示意图(保留作图痕迹).
例1题图
①满足条件的点P如解图①所示
例1题解图①
②若△APO∽△ABC时,在图②中画出所有满足条件的点P的示意图(保留作图痕迹)
例1题图
②满足条件的点P如解图②所示
例1题解图②
探究二: 若D为对称轴与x轴的交点,P是对称轴上的点,画出满足条件的点P,使得以O、D、P为顶点的三角形与△OBC相似.
例1题图
例1题解图③
满足条件的点P如解图③所示
【方法总结】二次函数中相似三角形的存在性一般要分情况讨论:以探究一为例,已知∠A公用,故需分∠AOP=∠ABC和____________两种情况.解决此类问题通常利用相似三角形的性质,列出线段比例关系,求解即可.
∠AOP=∠ACB
设问突破
二阶
例2 已知抛物线 y= x2- x+1与y轴交于点C,过点C的直线与x轴交于点A,与抛物线交于点B,点B的横坐标为4.
(1)如图①,点P在x轴上,连接CP,若△AOC∽△ACP,求点P的坐标;
例2题图①
【思维引导】设出点P的横坐标,利用相似关系列方程即可.
一题多设问
(1)当x=0时,y= x2- x+1=1.
∴点C的坐标是(0,1).
当x=4时,y= x2- x+1=3.
∴点B的坐标是(4,3).
由B(4,3)、C(0,1)可得直线BC的解析式为y= x+1.令y=0,解得x=-2.
∴ 点A的坐标是(-2,0).
∴AO=2,CO=1,
∴AC= = = ,
例2题图①
如解图①,设点P(p,0),
∴PA=|p+2|.
例2题图①
P
∵△AOC∽△ACP,
∴ = ,即 = ,
解得p= 或p=- (舍去),
∴当△AOC∽△ACP时,点P的坐标为( ,0);
(2)如图②,已知x轴上一动点Q(m,0),连接BQ,若△ABQ与△AOC相似,求m的值;
例2题图②
【思维引导】分两种情况:①△AOC∽△AQB;②△AOC∽△ABQ,再利用三角形相似的性质即可求解.
(2)如解图②,分两种情况讨论,
例2题解图②
①当△AOC∽△AQB时,过点B作BQ1⊥x轴于点Q1,
∴BQ1∥CO,
∴△AOC∽△AQ1B,
此时点Q1的坐标为(4,0),即m的值为4;
②当△AOC∽△ABQ时,过点B作BQ2⊥AB,
交x轴于点Q2,
∵∠CAO=∠Q2AB,∠AOC=∠ABQ2=90°,
∴△AOC∽△ABQ2,
例2题解图②
例2题解图②
∵A(-2,0),B(4,3),C(0,1),
∴AB= =3 ,
由(1)得AC= ,
∵△AOC∽△ABQ2,
∴ = ,即 = ,
∴AQ2= ,
此时点Q2的坐标为( ,0),即m的值为 .
综上所述,m的值为4或 ;
(3)如图③,设抛物线的对称轴与BC相交于点Q,点P是抛物线对称轴上的动点,且点P不与点Q重合,是否存在点P,使得以P、B、Q为顶点的三角形与△AOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
例2题图③
【思维引导】由已知条件可知△AOC是直角三角形,且点P在点Q上方,
∴∠ACO=∠BQP,∴只需要在△BPQ中确定一个直角即可.
分情况考虑:①∠BPQ=90°;②∠QBP=90°,再分别求解.
例2题图③
(3)存在.
由抛物线的解析式y= x2- x+1得对称轴为直线x= ,
由(1)得直线AC的解析式为y= x+1,
∵点Q在直线AC上,
∴将x= 代入y= x+1中,得y= ,
∴点Q的坐标为( , ).
如解图③,由题意得,点P在点Q的上方,设直线x= 与x轴的交点为M,则OC∥QM,
例2题解图③
∴∠OCA=∠MQA=∠BQP,
又∵∠AOC=90°,
∴要分为两种情况:
①当∠BP1Q=90°,即BP1∥x轴时,△BP1Q∽△AOC,
∵点B的坐标为(4,3),
∴点P1的坐标为( ,3);
例2题解图③
②当∠QBP2=90°,即BP2⊥BQ时,△QBP2∽△COA,
∴ = ,
由(1)得AC= ,设P2( ,p),
∵B(4,3),Q( , ),P1( ,3),
∴BP1=4- = ,P1Q=3- = ,
P2Q=p- ,
例2题解图③
在Rt△BQP1中,由勾股定理得BQ= = ,
∴ = ,解得p= ,
∴点P2的坐标为( , ) .
综上所述,满足条件的点P有两个,
点P的坐标为( ,3)或( , ).
题型六 二次函数与几何综合题
类型一~类型二
类型三 与三角形形状有关的问题
函数微技能—画图确定动点位置
一阶
例1. 如图,已知抛物线交x轴于A、B两点(点A在点B左侧),与y轴交于点C,连接AC.
例1题图
探究一:在抛物线上找一点P,使得△ACP为等腰三角形;
解:①若AC为等腰三角形的底边时,AP=________;在图①中画出所有满足条件的点P的示意图(保留作图痕迹).
【作图依据】________________________________________.
PC
满足条件的点P如解图①所示
例1题解图①
垂直平分线上的点到线段两端点的距离相等
例1题图
②若AC为等腰三角形的腰时,AC=________或AC= ________;在图②中画出所有满足条件的点P的示意图(保留作图痕迹).
AP
CP
满足条件的点P如解图②所示
例1题图
例1题解图②
探究二:在抛物线的对称轴上找一点E使得△BCE为等腰三角形.在图③中画出所有满足条件的点E的示意图(保留作图痕迹).
例1题图
满足条件的点E如解图③所示
例1题解图③
【方法总结】二次函数中等腰三角形的存在性一般要分情况讨论:常以已知边为________或________讨论;以探究一为例,已知边AC为底时,可以作底边的__________,所找点即为___________________的交点;若已知边AC为腰时,作图方法为:______________________,
_________________所找点即为____________________.
例1题图
底
腰
垂直平分线
垂直平分线与抛物线
分别以A、C为圆心,大于
AC长为半径画圆
两圆与抛物线的交点
例2 如图,已知抛物线交x轴于A、B两点(点A在点B左侧),与y轴交于点C,连接AC.
例2题图
探究一:在抛物线对称轴上找一点P,使得△ACP为直角三角形;
解:①若∠PAC=90°时,在图①中画出所有满足条件的点P的示意图(保留作图痕迹);
例2题图
①满足条件的点P如解图①所示
例2题解图①
②若∠PCA=90°时,在图②中画出所有满足条件的点P的示意图(保留作图痕迹);
②满足条件的点P如解图②所示
例2题图
例2题解图②
③若∠APC=90°时,在图③中画出所有满足条件的点P的示意图(保留作图痕迹);
③满足条件的点P如解图③所示
例2题图
例2题解图③
探究二:在抛物线上找一点E使得△BCE为直角三角形.在图④中画出所有满足条件的点E的示意图(保留作图痕迹).
满足条件的点E如解图④所示
例2题图
例2题解图④
【方法总结】二次函数中直角三角形的存在性一般要分情况讨论;以探究一为例,若∠PAC=90°,过点A作PA⊥AC交抛物线对称轴于点P;若∠PCA=90°,作图方法:__________________________________,所找点为_________________;若∠APC=90°,作图方法:________
___________________________,所找点为____________________.
过点C作PC⊥AC交抛物线对称轴于点P
PC与对称轴的交点
点D为圆心,AC长为直径作圆
以AC的中
对称轴与⊙D的交点
设问突破
二阶
一题多设问
例3 已知抛物线的解析式为y=-x2+2x+3,与x轴交于点A、B,与y轴交于点C,抛物线的顶点为D,对称轴DF交BC于点E,交x轴于点F.
(1)如图①,在抛物线上是否存在一点G,使得△BCG是以BC为底边的等腰三角形?若存在,求出点G的坐标;若不存在,请说明理由;
例3题图①
【思维引导】要使△BCG是以BC为底的等腰三角形,可作BC的垂直平分线,其与抛物线的交点即为所求点G.
例3题图①
解:(1)存在.
令抛物线中y=0,解得x=-1或x=3,
∴A(-1,0),B(3,0).
令抛物线中x=0,则y=3,∴C(0,3).
∴直线BC的解析式为y=-x+3,
线段BC的中点坐标为( , ),
∴易得BC的垂直平分线l的解析式为y=x,
联立抛物线与直线l的解析式可得
解得 或
∴满足条件的点G的坐标为( , )
或( , );
例3题图①
(2)如图②,在抛物线对称轴上是否存在一点M,使得△BCM是等腰三角形?若存在,求出点M的坐标,若不存在,请说明理由;
例3题图②
【思维引导】设点M坐标,然后表示出BM和CM,分BC为腰,BC为底边两种情况讨论,列方程,若方程有解,则存在,否则不存在.
(2)存在.
设点M(1,m),
由题意得BC=3 ,BM= ,
CM= ,
例3题图②
①当BC为腰时,
a.若BC=BM,即3 = ,
解得m=± ,则M1(1, ),M2(1,- );
b.若BC=CM,即3 = ,
解得m=3± ,则M3(1,3+ ),M4(1,3- );
②当BC为底边时,则CM=BM,
即 = ,
解得m=1,则M5(1,1).
例3题图②
综上所述,满足条件的点M的坐标为
(1, )或(1,- )或(1,3+ )或(1,3- )或(1,1);
(3)如图③,在抛物线的对称轴上是否存在一点H,使得△BCH是直角三角形?若存在,求出点H的坐标,若不存在,请说明理由;
例3题图③
【思维引导】分∠HCB=90°、∠HBC=90°、∠CHB=90°三种情况讨论,利用直角三角形的性质求解.
(3)存在.
设点H的坐标为(1,h),要使△BCH为直角三角形,需分三种情况讨论:
①当∠HCB=90°时,如解图①,
例3题解图①
∵点D为抛物线顶点,∴D(1,4),
∵CD2=12+(4-3)2=2,
BD2=(3-1)2+42=20,
BC2=32+32=18.
∴BC2+CD2=BD2.
∴∠DCB=90°.
∴当点H与点D重合时,∠BCH=90°,此时点H的坐标为(1,4);
例3题解图①
②当∠HBC=90°时,如解图②,
例3题解图②
∵OB=OC=3,
∴∠BCO=45°.
∴∠BEH=∠BCO=45°.
∴BE=BH.
∵EH⊥BF,
∴FH=BF=OB-OF=2.
∴此时点H的坐标为(1,-2);
③当∠CHB=90°时,如解图③,
设点H(1,h),过点C作CM⊥DF于点M,∴M(1,3),
∵∠CHM+∠BHE=90°,∠BHE+∠HBF=90°,
∴∠CHM=∠HBF,
又∵∠CMH=∠HFB=90°,∴△CHM∽△HBF,
∴ = ,即 = ,
解得h1= ,h2= ,
∴此时点H有两个,坐标分别为(1, )或(1, );
综上所述,点H的坐标为(1,4)或(1,-2)或(1, )或(1, );
例3题解图③
(4)如图④,在抛物线上是否存在一点N,使得△BCN是以BC为直角边的直角三角形?若存在,求出点N的坐标,若不存在,请说明理由.
【思维引导】△BCN是以BC为直角边的直角三角形,需分点B和点C分别为直角顶点两种情况讨论,结合△OBC是等腰直角三角形,利用等腰直角三角形的性质求解.
例3题图④
(4)存在.
设N(n,-n2+2n+3),分两种情况讨论;
①当∠NCB=90°时,如解图④,过点N作NG⊥y轴于点G,
G
(N)
∵OB=OC,
∴∠BCO=∠CBO=45°.
∴∠NCG=180°-∠BCO-∠BCD=45°.
∴CG=NG.
∵CG=OG-OC=-n2+2n+3-3=-n2+2n,NG=n,
∴-n2+2n=n.
解得n1=0(舍),n2=1.
∴N(1,4);
例3题图④
G
(N)
则∠HBN=90°-∠CBO=45°,
∴BH=NH.
∵BH=3-n,NH=-(-n2+2n+3)=n2-2n-3.
∴3-n=n2-2n-3,解得n1=3(舍),n2=-2.
∴N(-2,-5).
综上所述,点N的坐标为(1,4)或(-2,-5).
②当∠NBC=90°时,如解图⑤,过点N作NH⊥x轴于点H,
例3题解图⑤
类型四 与四边形形状有关的问题
函数微技能—画图确定动点位置
一阶
例1 如图,已知抛物线交x轴于A、B两点(点A在点B左侧),与y轴交于点C,连接AC.
例1题图
探究一:P是平面内一点,找出点P,使得以A、B、C、P为顶点的四边形为平行四边形;
解:①若AC为平行四边形的边时,AC∥BP,且AC=BP,在图①中画出所有满足条件的点P的示意图(保留作图痕迹).
例1题图
①满足条件的点P如解图①所示
例1题解图①
②若AC为平行四边形的对角线时,在图②中画出所有满足条件的点P的示意图(保留作图痕迹).
例1题图
②满足条件的点P如解图②所示
例1题解图②
讨论:探究菱形的存在性时,要区别于平行四边形的点为:①菱形各边相等;②菱形的对角线互相垂直.
探究二:M是x轴上的点,N是平面内一点,使得以B、C、M、N为顶点的四边形为菱形,在图③中画出满足条件的点M、N(保留作图痕迹).
例1题图
例1题解图③
满足条件的点M、N如解图③所示
【方法总结】二次函数中特殊四边形的存在性一般要分情况讨论:常以已知边为______或________讨论;以探究一为例,若AC为边时,过点B作BP∥AC,点P可在x轴上方,也可在x轴下方;作图依据:________________________________________;若AC为对角线时,作法:_________________________________________________.
边
对角线
一组对边平行且相等的四边形是平行四边形
取AC的中点D,连接BD并延长至点P,使得DP=BP
设问突破
二阶
一题多设问
例2 已知抛物线y=x2+6x+5与x轴交于A、B两点,与y轴交于点C,M为顶点,抛物线的对称轴l与x轴交于点D,与过A、C两点的直线交于点E.
(1)如图①,将抛物线沿x轴平移,使得点A落在点B处记为A′,此时点C的对应点为C′,求点C′的坐标,判断四边形AA′C′C的形状,并说明理由.
例2题图①
例2题图①
【思维引导】根据平移的性质可知,点A平移到点B的规律与点C平移到点C′的规律一致,即可得到点C′的坐标,再由AA′=CC′,AA′∥CC′即可判断四边形的形状.
(1)四边形AA′C′C是平行四边形,理由如下:
∵抛物线y=x2+6x+5与x轴交于A、B两点,与y轴交于点C,
∴当x=0时,y=5;当y=0,即x2+6x+5=0时,
解得x=-1或-5,
∴A(-5,0)、B(-1,0)、C(0,5),
∴AB=-1-(-5)=4,
∴由平移的性质得C′(4,5),AA′=CC′,AA′∥CC′,
∴四边形AA′C′C是平行四边形;
例2题图①
(2)如图②,设点G是抛物线上一点,过点G作GH∥x轴交对称轴l于点H,是否存在点G,使得以A、B、G、H为顶点的四边形是平行四边形?若存在,求出点G的坐标;若不存在,请说明理由;
例2题图②
【思维引导】由GH∥x轴,AB在x轴上可知AB∥GH,从而只需GH=AB即可得到以A、B、G、H为顶点的四边形是平行四边形.分点H在点G左侧和点H在点G右侧两种情况.
例2题图②
(2)存在,
由(1)得点A的坐标是(-5,0),点B的坐标是(-1,0).
∵点G在抛物线上,则设点G的坐标为(g,g2+6g+5),
∵GH∥x轴,点H在对称轴l上,
对称轴为直线x=- =-3,
∴H(-3,g2+6g+5),
∵GH∥AB,
∴要使以A、B、G、H为顶点的四边形为平行四边形,
需GH=AB=4,
例2题图②
即|g+3|=4,解得g=1或g=-7.
当g=1时,g2+6g+5=12,
此时点G的坐标为G1(1,12);
当g=-7时,g2+6g+5=12,
此时点G的坐标为G2(-7,12).
综上所述,满足条件的点G有两个,坐标分别为
(1,12)或(-7,12);
(3)如图③,G是坐标平面内一点,当以A、C、G、M为顶点的四边形是平行四边形时,求点G的坐标;
例2题图③
【思维引导】已知平行四边形的三个顶点,求第四个顶点,可顺次连接已知三点构成△ACM,分别以AC,AM,CM作为平行四边形的对角线进行分类讨论,利用“对角线互相平分的四边形是平行四边形”及中点坐标公式求解.
例2题图③
(3)∵抛物线的解析式为y=x2+6x+5=(x+3)2-4,
∴点M(-3,-4).
设点G(x,y),
∵A(-5,0),C(0,5),
分三种情况讨论:
①若AC为平行四边形AMCG的对角线时,
则AC与MG互相平分,
∴ = , = ,
∴ = , = ,
解得
∴G1(-2,9);
例2题图③
②若AM为平行四边形AGMC的对角线,则AM与CG互相平分,
∴ = , = ,
∴ = , = ,
解得
∴G2(-8,-9);
例2题图③
③若CM为平行四边形AMGC的对角线,则AG与CM互相平分,
∴ = , = ,
∴ = , = ,
解得
∴G3(2,1).
综上所述,点G的坐标为(-2,9)或
(-8,-9)或(2,1);
例2题图③
(4)如图④,设G是抛物线的对称轴上一点,K是坐标平面内一点,是否存在点G,使得以A,C,G,K 为顶点的四边形是矩形?若存在,求出点G的坐标;若不存在,请说明理由;
例2题图④
【思维引导】要使以A,C,G,K为顶点的四边形是矩形,只需△ACG是直角三角形即可,可分为①∠ACG=90°,②∠CAG=90°,③∠CGA=90°三种情况,分别利用勾股定理列方程即可求解.
(4)存在.
要使以A,C,G,K为顶点的四边形是矩形,则△ACG一定是直角三角形.
∵点G在对称轴上,
∴设点G的坐标为(-3,g),
由勾股定理得AC2=52+52=50,
AG2=(-5+3)2+g2=4+g2,
CG2=32+(g-5)2=g2-10g+34,
分三种情况讨论:
例2题图④
①若∠ACG=90°,
则AC2+CG2=AG2,
即50+g2-10g+34=4+g2,解得g=8,
此时点G的坐标为(-3,8);
②若∠CAG=90°,
则AC2+AG2=CG2,
即50+4+g2=g2-10g+34,
解得g=-2,
此时点G的坐标为(-3,-2);
例2题图④
③若∠CGA=90°,
则CG2+AG2=AC2,
即g2-10g+34+4+g2=50,
解得g1=6,g2=-1,
此时点G的坐标为(-3,6)或
(-3,-1);
综上所述,存在满足题意的点G,点G的坐标为(-3,8)或(-3,-2)或(-3,6)或(-3,-1);
例2题图④
(5)如图⑤,设Q是抛物线上一点,点R是坐标平面内一点,是否存在四边形AQCR是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.
例2题图⑤
【思维引导】由四边形AQCR是菱形可确定AC是对角线,则Q、R均在AC的垂直平分线上,联立方程求解即可.
(5)存在.
如解图,过点O作OI⊥AC于点I,
I
Q1
Q2
∵四边形AQCR是菱形,∴QR垂直平分AC.
∵OA=OC=5,
∴AI=CI,
∴OI是AC的垂直平分线,
∴点Q、R在AC的垂直平分线上,
∴点Q是直线OI与抛物线的交点.
∵I是AC的中点,
∴xI= =- ,yI= = ,
∴点I的坐标为(- , ),
例2题图⑤
I
Q1
Q2
例2题图⑤
I
Q1
Q2
设直线OI的解析式为y=tx,将点I的坐标代入,可得t=-1,
∴直线OI的解析式为y=-x,
联立
解得 或
∴存在满足题意的点Q,
点Q的坐标为( , )或( , ).
类型五 与三角形相似有关的问题
函数微技能—画图确定动点位置
一阶
例1 如图,已知抛物线交x轴于A、B两点(点A在点B左侧),与y轴交于点C,连接AC.
例1题图
探究一:P是线段AC上一点,找出点P,使得以A、O、P为顶点的三角形与△ABC相似;
解:①若△AOP∽△ABC时,在图①中画出所有满足条件的点P的示意图(保留作图痕迹).
例1题图
①满足条件的点P如解图①所示
例1题解图①
②若△APO∽△ABC时,在图②中画出所有满足条件的点P的示意图(保留作图痕迹)
例1题图
②满足条件的点P如解图②所示
例1题解图②
探究二: 若D为对称轴与x轴的交点,P是对称轴上的点,画出满足条件的点P,使得以O、D、P为顶点的三角形与△OBC相似.
例1题图
例1题解图③
满足条件的点P如解图③所示
【方法总结】二次函数中相似三角形的存在性一般要分情况讨论:以探究一为例,已知∠A公用,故需分∠AOP=∠ABC和____________两种情况.解决此类问题通常利用相似三角形的性质,列出线段比例关系,求解即可.
∠AOP=∠ACB
设问突破
二阶
例2 已知抛物线 y= x2- x+1与y轴交于点C,过点C的直线与x轴交于点A,与抛物线交于点B,点B的横坐标为4.
(1)如图①,点P在x轴上,连接CP,若△AOC∽△ACP,求点P的坐标;
例2题图①
【思维引导】设出点P的横坐标,利用相似关系列方程即可.
一题多设问
(1)当x=0时,y= x2- x+1=1.
∴点C的坐标是(0,1).
当x=4时,y= x2- x+1=3.
∴点B的坐标是(4,3).
由B(4,3)、C(0,1)可得直线BC的解析式为y= x+1.令y=0,解得x=-2.
∴ 点A的坐标是(-2,0).
∴AO=2,CO=1,
∴AC= = = ,
例2题图①
如解图①,设点P(p,0),
∴PA=|p+2|.
例2题图①
P
∵△AOC∽△ACP,
∴ = ,即 = ,
解得p= 或p=- (舍去),
∴当△AOC∽△ACP时,点P的坐标为( ,0);
(2)如图②,已知x轴上一动点Q(m,0),连接BQ,若△ABQ与△AOC相似,求m的值;
例2题图②
【思维引导】分两种情况:①△AOC∽△AQB;②△AOC∽△ABQ,再利用三角形相似的性质即可求解.
(2)如解图②,分两种情况讨论,
例2题解图②
①当△AOC∽△AQB时,过点B作BQ1⊥x轴于点Q1,
∴BQ1∥CO,
∴△AOC∽△AQ1B,
此时点Q1的坐标为(4,0),即m的值为4;
②当△AOC∽△ABQ时,过点B作BQ2⊥AB,
交x轴于点Q2,
∵∠CAO=∠Q2AB,∠AOC=∠ABQ2=90°,
∴△AOC∽△ABQ2,
例2题解图②
例2题解图②
∵A(-2,0),B(4,3),C(0,1),
∴AB= =3 ,
由(1)得AC= ,
∵△AOC∽△ABQ2,
∴ = ,即 = ,
∴AQ2= ,
此时点Q2的坐标为( ,0),即m的值为 .
综上所述,m的值为4或 ;
(3)如图③,设抛物线的对称轴与BC相交于点Q,点P是抛物线对称轴上的动点,且点P不与点Q重合,是否存在点P,使得以P、B、Q为顶点的三角形与△AOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
例2题图③
【思维引导】由已知条件可知△AOC是直角三角形,且点P在点Q上方,
∴∠ACO=∠BQP,∴只需要在△BPQ中确定一个直角即可.
分情况考虑:①∠BPQ=90°;②∠QBP=90°,再分别求解.
例2题图③
(3)存在.
由抛物线的解析式y= x2- x+1得对称轴为直线x= ,
由(1)得直线AC的解析式为y= x+1,
∵点Q在直线AC上,
∴将x= 代入y= x+1中,得y= ,
∴点Q的坐标为( , ).
如解图③,由题意得,点P在点Q的上方,设直线x= 与x轴的交点为M,则OC∥QM,
例2题解图③
∴∠OCA=∠MQA=∠BQP,
又∵∠AOC=90°,
∴要分为两种情况:
①当∠BP1Q=90°,即BP1∥x轴时,△BP1Q∽△AOC,
∵点B的坐标为(4,3),
∴点P1的坐标为( ,3);
例2题解图③
②当∠QBP2=90°,即BP2⊥BQ时,△QBP2∽△COA,
∴ = ,
由(1)得AC= ,设P2( ,p),
∵B(4,3),Q( , ),P1( ,3),
∴BP1=4- = ,P1Q=3- = ,
P2Q=p- ,
例2题解图③
在Rt△BQP1中,由勾股定理得BQ= = ,
∴ = ,解得p= ,
∴点P2的坐标为( , ) .
综上所述,满足条件的点P有两个,
点P的坐标为( ,3)或( , ).
同课章节目录
