江西省萍乡二中北师大版数学必修一第一章第一节《集合的含义与表示》课件(23张ppt)
文档属性
| 名称 | 江西省萍乡二中北师大版数学必修一第一章第一节《集合的含义与表示》课件(23张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-08 00:00:00 | ||
图片预览







文档简介
课件23张PPT。问题提出 是日常生活中的一个常用词,现代汉语解释为:许多的人或物聚在一起. 在现代数学中,研究集合的数学理论称为集合论,它是
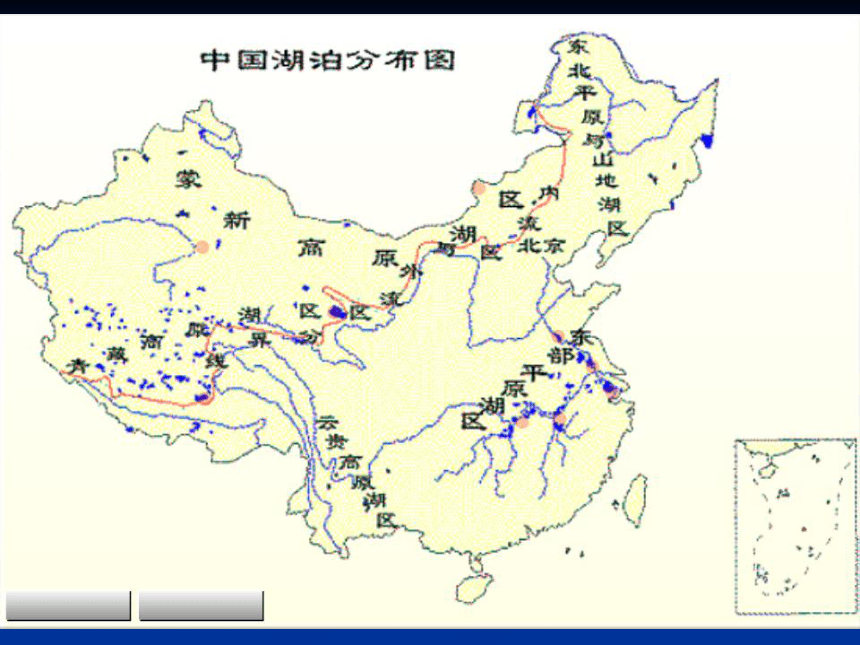
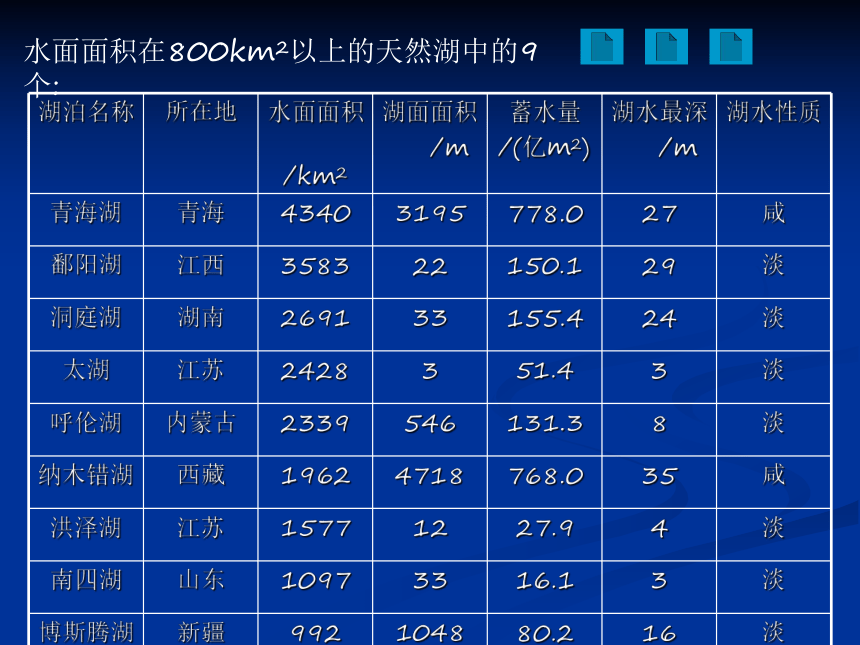
现代数学这所大厦的基石.集合的含义我们怎样理解数学中的“集合”?合集 我国地域辽阔,湖泊众多,统计显示,水面面积在1km2以上的天然湖泊有2800多个;水面在100km2以上的天然湖有130多个;此外,还有大大小小的人工湖(水库).水面面积在800km2以上的天然湖中的9个:集合的含义比如, “蓄水量在100~700亿m3的天然湖的
全体” 就构成一个集合.指定的某些对象的全体称为集合.集合常用大写字母A,B,C,…标记;
集合中的每个对象叫做这个集合的元素;若元素a在集合A中,就说元素属于集合,记作
a ∈A; 在上述集合中洞庭湖、鄱阳湖、呼伦湖都是
这个集合中的元素;一些常见的数集及其记法自然数组成的集合简称自然数集,记作N;
正整数组成的集合简称正整数集,记作N+ ;
整数组成的集合简称整数集,记作Z;
有理数组成的集合简称有理数集,记作Q;
实数组成的集合简称实数集,记作R.比如,复习:数的分类实数有理数无理数整数分数正整数负整数零自然数巩固练习二.课本 练习1用符号∈或 填空:0 N; 0 N+; -1 N; -1 Z; 1 Q;
Q; 3.14 Q; 3.14 Z; Q; Z;
R; N; Z; Q; R.
∈∈∈∈∈∈∈集合的常用表示法比如, “方程x2-5x=0 在实数内解的全体” 组成的集合C可以这样表示: C={0,5},把集合中的元素一一列举出来,写在大括号内的方法叫做列举法;也可以这样表示: C={方程x2-5x=0 在实数内的解} 用确定的条件表示某些对象是否属于这个集合的方法叫做描述法.描述法(或称为集合的特征性质描述法)的一般形式为:A= {x∈U︱p(x)} .或C={x∈R︱x2-5x=0 }.探究:“由大于3小于10的整数组成的集合”如何表示.参考:1.{4,5,6,7,8,9},变式1 : “由大于3的整数组成的集合” 如何表示.变式2:“由大于3小于10的实数组成的集合”如何表示.参考:1.{x∈Z︱ x >3}; 参考: {x︱ 3 它有什么特征??记作?.练习2:⑴ 0 ? (填∈或?)
⑵ ? {? }(填∈或?) 方程例1若x∈R,则数集{1,x,x2}中元素x
应满足什么条件.解:∵x≠1且x2≠1且x2≠x,∴ x≠1且x≠-1且x≠0.例题例2设x∈R,y∈R,观察下面四个集合
A={ y=x2-1 }
B={ x | y=x2-1 }
C={ y | y=x2-1 }
D={ (x, y) | y=x2-1 }
它们表示含义相同吗?例3若以方程x2-5x+6=0
和方程x2-x-2=0的解为元素的集为
M,则M中元素的个数为A.1 B.2 C.3 D.4( C )例4已知集合
A={x|ax2+4x+4=0,x∈R,a∈R}
只有一个元素,求a的值与这个元素.解:当a=0时,x=-1.当a≠0时,?=16-4×4a=0.a=1. 此时x=-2.∴a=1时这个元素为-2. ∴a=0时这个元素为-1. 小结集合与元素的概念;
常用数集的表示方法;
常用的集合表示法;
集合的性质;
集合的分类;
空集. 作业
P6习题1.1 A组: 1. 2. 3.
现代数学这所大厦的基石.集合的含义我们怎样理解数学中的“集合”?合集 我国地域辽阔,湖泊众多,统计显示,水面面积在1km2以上的天然湖泊有2800多个;水面在100km2以上的天然湖有130多个;此外,还有大大小小的人工湖(水库).水面面积在800km2以上的天然湖中的9个:集合的含义比如, “蓄水量在100~700亿m3的天然湖的
全体” 就构成一个集合.指定的某些对象的全体称为集合.集合常用大写字母A,B,C,…标记;
集合中的每个对象叫做这个集合的元素;若元素a在集合A中,就说元素属于集合,记作
a ∈A; 在上述集合中洞庭湖、鄱阳湖、呼伦湖都是
这个集合中的元素;一些常见的数集及其记法自然数组成的集合简称自然数集,记作N;
正整数组成的集合简称正整数集,记作N+ ;
整数组成的集合简称整数集,记作Z;
有理数组成的集合简称有理数集,记作Q;
实数组成的集合简称实数集,记作R.比如,复习:数的分类实数有理数无理数整数分数正整数负整数零自然数巩固练习二.课本 练习1用符号∈或 填空:0 N; 0 N+; -1 N; -1 Z; 1 Q;
Q; 3.14 Q; 3.14 Z; Q; Z;
R; N; Z; Q; R.
∈∈∈∈∈∈∈集合的常用表示法比如, “方程x2-5x=0 在实数内解的全体” 组成的集合C可以这样表示: C={0,5},把集合中的元素一一列举出来,写在大括号内的方法叫做列举法;也可以这样表示: C={方程x2-5x=0 在实数内的解} 用确定的条件表示某些对象是否属于这个集合的方法叫做描述法.描述法(或称为集合的特征性质描述法)的一般形式为:A= {x∈U︱p(x)} .或C={x∈R︱x2-5x=0 }.探究:“由大于3小于10的整数组成的集合”如何表示.参考:1.{4,5,6,7,8,9},变式1 : “由大于3的整数组成的集合” 如何表示.变式2:“由大于3小于10的实数组成的集合”如何表示.参考:1.{x∈Z︱ x >3}; 参考: {x︱ 3
⑵ ? {? }(填∈或?) 方程例1若x∈R,则数集{1,x,x2}中元素x
应满足什么条件.解:∵x≠1且x2≠1且x2≠x,∴ x≠1且x≠-1且x≠0.例题例2设x∈R,y∈R,观察下面四个集合
A={ y=x2-1 }
B={ x | y=x2-1 }
C={ y | y=x2-1 }
D={ (x, y) | y=x2-1 }
它们表示含义相同吗?例3若以方程x2-5x+6=0
和方程x2-x-2=0的解为元素的集为
M,则M中元素的个数为A.1 B.2 C.3 D.4( C )例4已知集合
A={x|ax2+4x+4=0,x∈R,a∈R}
只有一个元素,求a的值与这个元素.解:当a=0时,x=-1.当a≠0时,?=16-4×4a=0.a=1. 此时x=-2.∴a=1时这个元素为-2. ∴a=0时这个元素为-1. 小结集合与元素的概念;
常用数集的表示方法;
常用的集合表示法;
集合的性质;
集合的分类;
空集. 作业
P6习题1.1 A组: 1. 2. 3.
