江西省萍乡市二中北师大版数学必修一第三章第六节《指数函数·幂函数·对数函数增长的比较》课件(共21张PPT)
文档属性
| 名称 | 江西省萍乡市二中北师大版数学必修一第三章第六节《指数函数·幂函数·对数函数增长的比较》课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 367.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-09 08:18:34 | ||
图片预览





文档简介
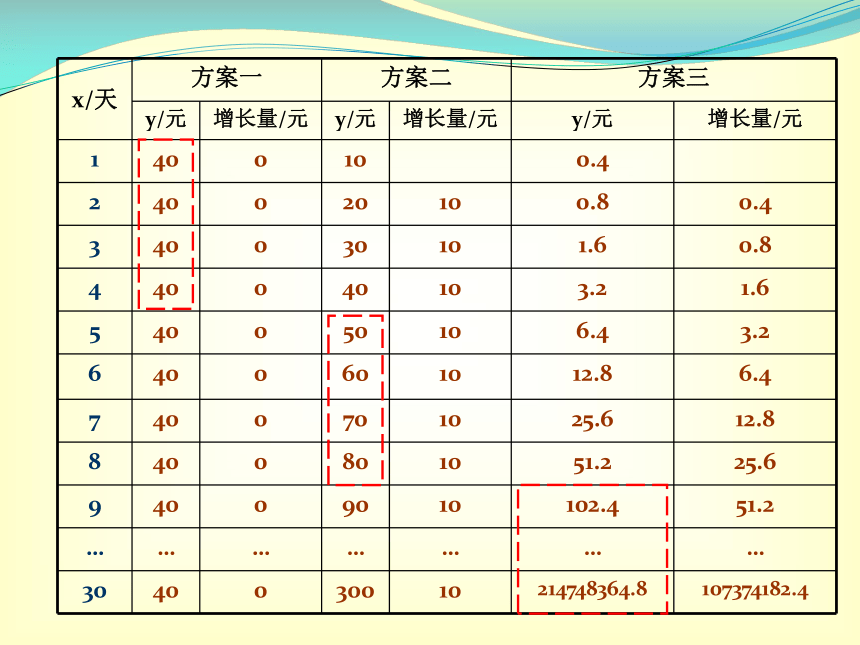
课件21张PPT。幂、指、对函数增长的比较萍乡二中 邢江海例题:例1、假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:方案一:每天回报40元;方案二:第一天回报10元,以后每天比前一天多 回报10元;方案三:第一天回报0.4元,以后每天的回报比前 一天翻一番。请问,你会选择哪种投资方案呢?思考 比较三种方案每天回报量 哪个方案在某段时间内的总回报量最多,我们就在那段时间选择该方案。(2) 比较三种方案一段时间内的总回报量投入资金相同,回报量多者为优解:设第x天所得回报为y元,则 方案二:第一天回报10元,以后每天比前一天多回 报10元; y=10x (x∈N*)方案三:第一天回报0.4元,以后每天的回报比前一天翻一番。
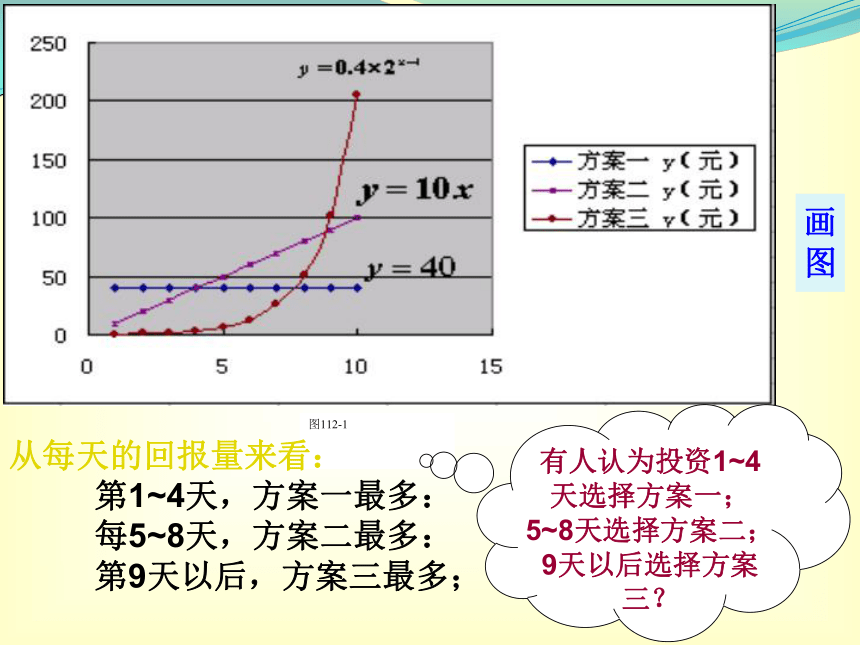
y=0.4×2x-1 (x∈N*)方案一:每天回报40元; y=40 (x∈N*)三种方案的回报情况图112-1从每天的回报量来看: 第1~4天,方案一最多: 每5~8天,方案二最多: 第9天以后,方案三最多;有人认为投资1~4天选择方案一;5~8天选择方案二;9天以后选择方案三?画
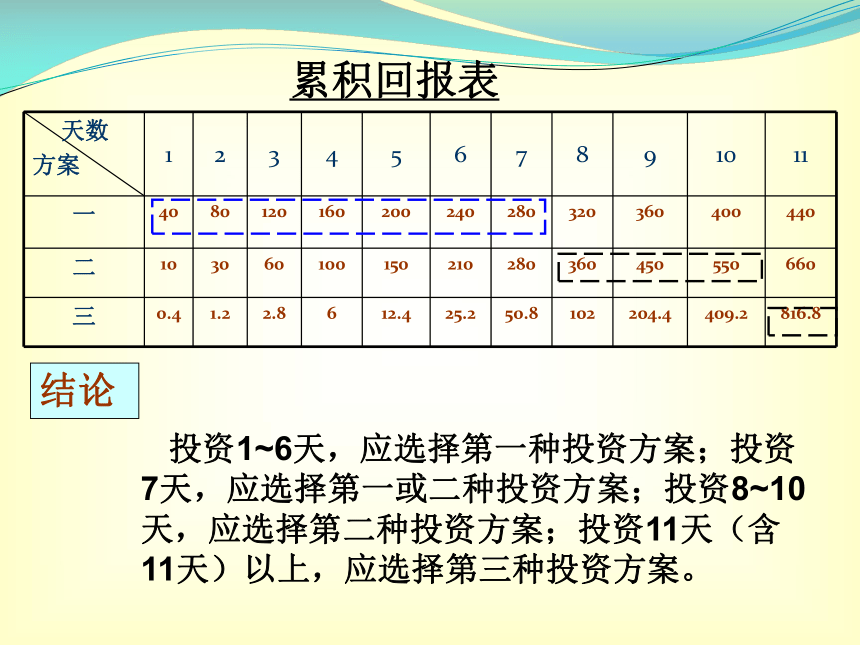
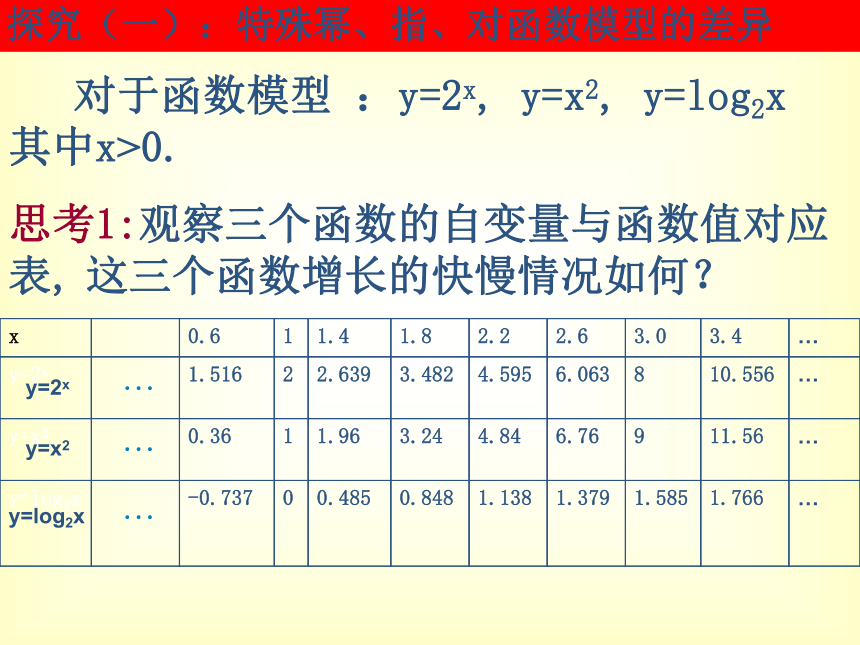
图累积回报表结论 投资1~6天,应选择第一种投资方案;投资7天,应选择第一或二种投资方案;投资8~10天,应选择第二种投资方案;投资11天(含11天)以上,应选择第三种投资方案。 问题提出 1.指数函数y=ax (a>1),对数函数 y=logax(a>1)和幂函数y=xn (n>0)在区间(0,+∞)上的单调性如何? 2.利用这三类函数模型解决实际问题,其增长速度是有差异的,我们怎样认识这种差异呢? 探究(一):特殊幂、指、对函数模型的差异 对于函数模型 :y=2x, y=x2, y=log2x 其中x>0. 思考2:对于函数模型y=2x和y=x2,观察下列自变量与函数值对应表: 当x>0时,你估计函数y=2x和y=x2的图象共有几个交点? 思考3:在同一坐标系中这三个函数图象的相对位置关系如何?请画出其大致图象. 思考4:根据图象,不等式log2x<2xlog2x1和n>0,在区间
(0,+∞)上ax是否恒大于xn? ax是否恒小于xn?思考2:当a>1,n>0时,在区间(0,+∞)上, ax与xn的大小关系应如何阐述? 思考3:一般地,指数函数y=ax (a>1)和幂函数y=xn(n>0)在区间(0,+∞)上,其增长的快慢情况是如何变化的?思考4:对任意给定的a>1和n>0,在区间 (0,+∞)上,logax是否恒大于xn? logax是否恒小于xn?思考5:随着x的增大,logax增长速度的快慢程度如何变化? xn增长速度的快慢程度如何变化?思考6:当x充分大时,logax(a>1)与xn (n>0)谁的增长速度相对较快?思考7:一般地,对数函数y=logax(a>1)和幂函数y=xn(n>0) 在区间(0,+∞)上,其增长的快慢情况是如何变化的?思考8:对于指数函数y=ax(a>1),对数函数 y=logax(a>1)和幂函数y=xn(n>0),总存在一个x0,使x>x0时,ax,logax,xn三者的大小关系如何?思考9:指数函数y=ax (01),y=logax (a>1)和y=xn (n>0)都是增函数。(2)、随着x的增大, y=ax (a>1)的增长速度越来越快,会远远大于y=xn (n>0)的增长速度。(3)、随着x的增大, y=logax (a>1)的增长速度越来越慢,会远远小于y=xn (n>0)的增长速度。总存在一个x0,当x>x0时,就有
logax
y=0.4×2x-1 (x∈N*)方案一:每天回报40元; y=40 (x∈N*)三种方案的回报情况图112-1从每天的回报量来看: 第1~4天,方案一最多: 每5~8天,方案二最多: 第9天以后,方案三最多;有人认为投资1~4天选择方案一;5~8天选择方案二;9天以后选择方案三?画
图累积回报表结论 投资1~6天,应选择第一种投资方案;投资7天,应选择第一或二种投资方案;投资8~10天,应选择第二种投资方案;投资11天(含11天)以上,应选择第三种投资方案。 问题提出 1.指数函数y=ax (a>1),对数函数 y=logax(a>1)和幂函数y=xn (n>0)在区间(0,+∞)上的单调性如何? 2.利用这三类函数模型解决实际问题,其增长速度是有差异的,我们怎样认识这种差异呢? 探究(一):特殊幂、指、对函数模型的差异 对于函数模型 :y=2x, y=x2, y=log2x 其中x>0. 思考2:对于函数模型y=2x和y=x2,观察下列自变量与函数值对应表: 当x>0时,你估计函数y=2x和y=x2的图象共有几个交点? 思考3:在同一坐标系中这三个函数图象的相对位置关系如何?请画出其大致图象. 思考4:根据图象,不等式log2x<2x
(0,+∞)上ax是否恒大于xn? ax是否恒小于xn?思考2:当a>1,n>0时,在区间(0,+∞)上, ax与xn的大小关系应如何阐述? 思考3:一般地,指数函数y=ax (a>1)和幂函数y=xn(n>0)在区间(0,+∞)上,其增长的快慢情况是如何变化的?思考4:对任意给定的a>1和n>0,在区间 (0,+∞)上,logax是否恒大于xn? logax是否恒小于xn?思考5:随着x的增大,logax增长速度的快慢程度如何变化? xn增长速度的快慢程度如何变化?思考6:当x充分大时,logax(a>1)与xn (n>0)谁的增长速度相对较快?思考7:一般地,对数函数y=logax(a>1)和幂函数y=xn(n>0) 在区间(0,+∞)上,其增长的快慢情况是如何变化的?思考8:对于指数函数y=ax(a>1),对数函数 y=logax(a>1)和幂函数y=xn(n>0),总存在一个x0,使x>x0时,ax,logax,xn三者的大小关系如何?思考9:指数函数y=ax (0
logax
