人教版八年级下册第十七章 勾股定理 单元验收卷(含解析)
文档属性
| 名称 | 人教版八年级下册第十七章 勾股定理 单元验收卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-03 07:01:39 | ||
图片预览



文档简介
第十七章 勾股定理 单元验收卷
满分:120分 时间:90分钟
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题(共30分)
1.(本题3分)观察下列各组数:①7,12,15,②8,15,17,③7,24,25,④12,15,20,其中能作为直角三角形三边长的有( )
A.1组 B.2组 C.3组 D.4组
2.(本题3分)在中,、、的对应边分别是a、b、c,若,则下列等式中成立的是( )
A. B. C. D.
3.(本题3分)三角形的三边a,b,c满足,则此三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
4.(本题3分)如图,一棵树(树干与地面垂直)高米,在一次强台风中树被强风折断,倒下后的树顶C与树根A的距离为米,则这棵树断裂处点B离地面的高度的值为( )
A.2.4米 B.2.6米 C.0.6米 D.1米
(6) (7) (10)
5.(本题3分)一架5m的梯子,斜靠在一竖直的墙上,这时梯子的底端距墙角4m,若梯子的顶端下滑1m,则梯子的底端将滑动( )
A.0m B.1m C. D.
6.(本题3分)某酒店打算在一段楼梯面上铺上宽为2米的地毯,台阶的侧面如图所示,如果这种地毯每平方米售价为80元,则购买这种地毯至少需要( )
A.2560元 B.2620元 C.2720元 D.2840元
7.(本题3分)如图,在中,,,点在上,,,则的长为( )
A. B. C. D.
8.(本题3分)在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,下列说法错误的是( )
A.如果∠C-∠B=∠A,那么△ABC是直角三角形,且∠C=90°
B.如果c2=a2+b2,那么△ABC是直角三角形,且∠C=90°
C.如果,那么△ABC是直角三角形,且∠C=90°
D.如果∠A:∠B:∠C=5:2:3,那么△ABC是直角三角形 ,且∠A=90°
9.(本题3分)下列各命题的逆命题成立的是( )
A.全等三角形的对应角相等 B.若两数相等,则它们的绝对值相等
C.若两个角是45,那么这两个角相等 D.两直线平行,同位角相等
10.(本题3分)一只蚂蚁从圆柱体的下底面点沿着侧面爬到上底面点,已知圆柱的底面半径为,高为(取3),则蚂蚁所走过的最短路径是( )
A.8 B.9 C.10 D.12
评卷人得分
二、填空题(共30分)
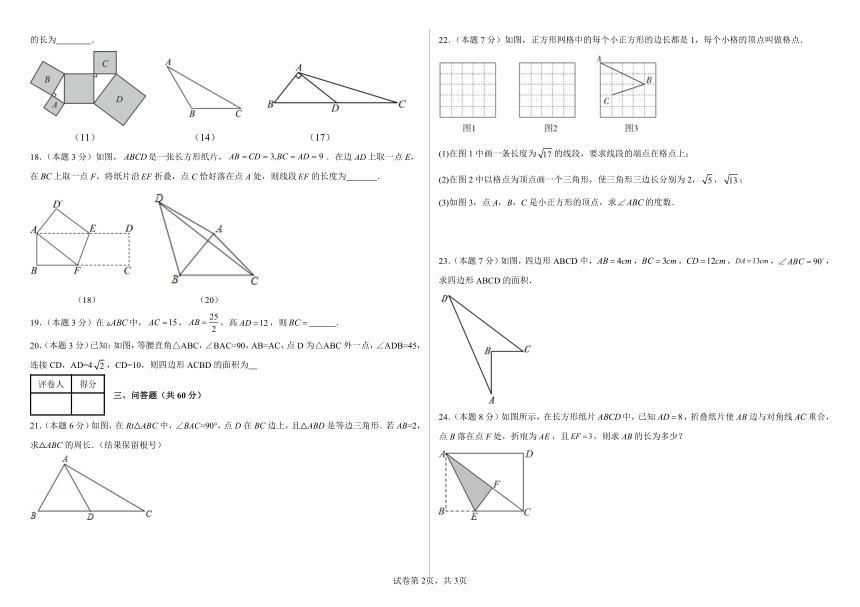
11.(本题3分)如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形,,的面积依次为,,,则正方形的面积为 .
12.(本题3分)一艘轮船以的速度离开港口向东北方向航行,另一艘轮船同时离开港口以的速度向东南方向航行,它们离开港口半小时后相距 .
13.(本题3分)一个三角形的三边长度之比为15:8:17,则这个三角形的最大角是 度.
14.(本题3分)已知:在中,,,,则 .
15.(本题3分)在平面直角坐标系中,,则线段
16.(本题3分)已知a、b、c是的三边长,且满足关系,则的形状是 .
17.(本题3分)如图,在中,是边上的中线,,,,则的长为 .
(14) (17)
18.(本题3分)如图,是一张长方形纸片,.在边上取一点E,在上取一点F,将纸片沿折叠,点C恰好落在点A处,则线段的长度为 .
(20)
19.(本题3分)在中,,,高,则 .
20.(本题3分)已知:如图,等腰直角△ABC,∠BAC=90,AB=AC,点D为△ABC外一点,∠ADB=45,连接CD,AD=4,CD=10,则四边形ACBD的面积为
评卷人得分
三、问答题(共60分)
21.(本题6分)如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形.若AB=2,求△ABC的周长.(结果保留根号)
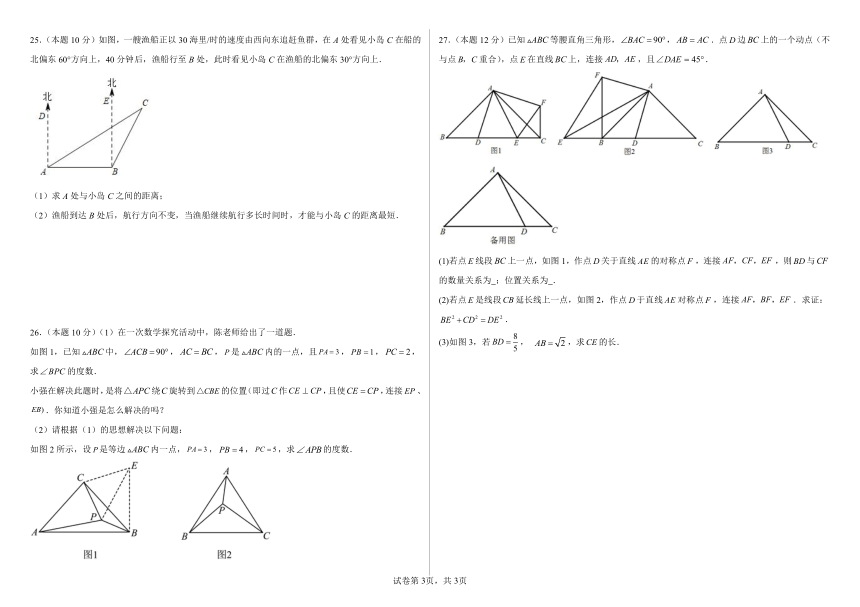
22.(本题7分)如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
(1)在图1中画一条长度为的线段,要求线段的端点在格点上;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2,,;
(3)如图3,点A,B,C是小正方形的顶点,求的度数.
23.(本题7分)如图,四边形ABCD中,,,,,,求四边形ABCD的面积.
24.(本题8分)如图所示,在长方形纸片中,已知,折叠纸片使边与对角线重合,点B落在点F处,折痕为,且,则求的长为多少?
25.(本题10分)如图,一艘渔船正以30海里/时的速度由西向东追赶鱼群,在A处看见小岛C在船的北偏东60°方向上,40分钟后,渔船行至B处,此时看见小岛C在渔船的北偏东30°方向上.
(1)求A处与小岛C之间的距离;
(2)渔船到达B处后,航行方向不变,当渔船继续航行多长时间时,才能与小岛C的距离最短.
26.(本题10分)(1)在一次数学探究活动中,陈老师给出了一道题.
如图1,已知中,,,是内的一点,且,,,求的度数.
小强在解决此题时,是将绕旋转到的位置(即过作,且使,连接、.你知道小强是怎么解决的吗?
(2)请根据(1)的思想解决以下问题:
如图2所示,设是等边内一点,,,,求的度数.
27.(本题12分)已知等腰直角三角形,,.点边上的一个动点(不与点重合),点在直线上,连接,且.
(1)若点线段上一点,如图1,作点关于直线的对称点,连接,则与的数量关系为 ;位置关系为 .
(2)若点是线段延长线上一点,如图2,作点于直线对称点,连接.求证:.
(3)如图3,若, ,求的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】本题考查了勾股定理的逆定理;熟练掌握勾股定理的逆定理,并能进行推理论证与计算是解决问题的关键.
由勾股定理的逆定理得出②③能构成直角三角形,①④不能构成直角三角形;即可得出结论.
【详解】解:,
∴7,12,15不能构成直角三角形,
∴①不能作为直角三角形三边长;
∵,
∴8,15,17能构成直角三角形,
∴②能作为直角三角形三边长;
,
∴7,24,25能构成直角三角形,
∴③能作为直角三角形三边长;
,
∴12,15,20不能构成直角三角形,
∴④不能作为直角三角形三边长;
∴能作为直角三角形三边长的有2组,
故选:B.
2.C
【分析】由已知两角之和为90度,利用三角形内角和定理得到三角形为直角三角形,利用勾股定理即可得到结果.
【详解】解:∵在中,,
∴,
∴为直角三角形,
则根据勾股定理得:.
故选:C.
【点睛】此题考查了勾股定理,熟练掌握勾股定理是解题的关键.
3.B
【分析】
本题考查了勾股定理的逆定理.先根据完全平方公式对已知等式进行化简,再根据勾股定理的逆定理进行判定.
【详解】
解:∵,
∴,
∴,
∴三角形是直角三角形.
故选:B.
4.D
【分析】设这棵树断裂处点B离地面的高度的值为,则,然后根据勾股定理列方程求解即可.
【详解】解:设这棵树断裂处点B离地面的高度的值为x,则、,
∵是直角三角形,
∴,即,解得:,即.
故选:D.
【点睛】本题主要考查的是勾股定理的应用,根据勾股定理列出方程是解题关键.
5.D
【分析】本题考查了勾股定理的应用.由题意画出图形,由勾股定理求出,则,再由勾股定理求出的长,即可解决问题.
【详解】解:由题意画出图形如下:
在中,,,
,
在中,,,
,
,
即梯子的底端将滑动,
故选:D.
6.C
【分析】根据题意,结合图形,先把楼梯的横竖向上向左平移,构成一个矩形,再求得其面积,则购买地毯的钱数可求.
【详解】
利用平移线段,把楼梯的横竖向上向左平移,构成一个矩形,长宽分别为米、5米,
∴地毯的长度为12+5=17米,地毯的面积为17×2=34平方米,
∴购买这种地毯至少需要80×34=2720元.
故选C.
【点睛】本题考查的知识点是勾股定理的应用,生活中的平移现象,解题关键是要注意利用平移的知识,把要求的所有线段平移到一条直线上进行计算.
7.D
【分析】由勾股定理求出CD=1,再根据∠ADC是△ABD的外角,证出∠B=∠BAD,从而有BD=AD,即可求出BC的长.
【详解】解:在Rt△ACD中,由勾股定理得:
CD= =1,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD,
∵∠ADC=2∠B,
∴∠B=∠BAD,
∴BD=AD=,
∴BC=+1.
故选:D.
【点睛】本题主要考查了勾股定理、三角形外角的性质、等腰三角形的判定等知识,利用外角证出∠B=∠BAD是解题的关键.
8.C
【分析】根据直角三角形的定义,勾股定理以及三角形的内角和进行判断即可.
【详解】解:A.因为∠C﹣∠B=∠A,∠C+∠B+∠A=180°,所以2∠C=180°,即∠C=90°.故选项正确;
B.因为,则△ABC是直角三角形,且∠C=90°,故该选项正确;
C.因为,所以,则△ABC是直角三角形,且∠B=90°.故选项错误;
D.因为∠A:∠B:∠C=5:2:3,所以∠A=90°,∠B=36°,∠C=54°,则△ABC是直角三角形,且∠A=90°.故选项正确.
故选:C.
【点睛】本题主要考查了直角三角形的定义,熟练掌握直角三角形的定义以及勾股定理的逆定理是解题的关键.
9.D
【分析】先分别写出四个命题的逆命题,根据三角形全等的判定方法对A的逆命题进行判断;根据相反数的绝对值相等对B的逆命题进行判断;根据两个角相等,这两个角可为任意角度可对C的逆命题进行判断;根据平行线的判定定理对D的逆命题进行判断.
【详解】A. “全等三角形的对应角相等”的逆命题为“对应角相等的两三角形全等”,此逆命题为假命题,所以A选项错误;
B. “若两数相等,则它们的绝对值相等”的逆命题为“若两数的绝对值相等,则这两数相等”,此逆命题为假命题,所以B选项错误;
C. “若两个角是45°,那么这两个角相等”的逆命题为“若两个角相等,你们这两个角是45°”,此逆命题为假命题,所以C选项错误;
D. “两直线平行,同位角相等”的逆命题为“同位角相等,两直线平行”,此逆命题为真命题,所以D选项正确.
故选D.
【点睛】此题考查命题与定理,解题关键在于掌握掌握各性质定义.
10.C
【分析】要求最短路径,首先要把圆柱的侧面展开,利用两点之间线段最短,然后利用勾股定理即可求解.
【详解】解:把圆柱侧面展开,展开图如图所示,点、的最短距离为线段的长.
在中,,,为底面半圆弧长,
,
所以.
故选:C.
【点睛】本题考查了平面展开-最短路径问题,解题的关键是会将圆柱的侧面展开,并利用勾股定理解答.
11.
【分析】本题考查的是勾股定理,根据勾股定理可得正方形A、B的面积之和等于正方形E的面积,正方形C、E的面积之和等于正方形D的面积,即可得到结果.
【详解】
由题意得,正方形的面积为,
则正方形的面积.
故答案为:.
12.26
【分析】先算出它们离开港口半小时后各自航行的路程,再根据勾股定理求解即可.
【详解】解:由题意可知,两艘轮船航行的路线成垂直关系,
它们离开港口半小时后各自航行的路程分别为、,
∴它们离开港口半小时后相距,
故答案为:26.
【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.
13.90
【分析】一个三角形的三边符合a2+b2=c2,根据勾股定理的逆定理,这个三角形是直角三角形.
【详解】解:设三角形的三边分别为8x,15x,17x,
∵(8x)2+(15x)2=(17x)2,
根据勾股定理的逆定理,这个三角形是直角三角形,最大角是90°.
故答案为:90.
【点睛】本题考查了勾股定理的逆定理:已知三角形ABC的三边满足a2+b2=c2,则三角形ABC是直角三角形.
14.
【分析】本题主要考查了勾股定理,含30度角的直角三角形的性质,过点A作交延长线于H,利用平角的定义和三角形内角和定理求出,则,,利用勾股定理得到,代值计算即可.
【详解】解:如图所示,过点A作交延长线于H,
∵,
∴,
∴,
∴,
∴,
在中,由勾股定理得,
在中,由勾股定理得,
∴,即,
∴(负值舍去),
故答案为:.
15.
【分析】本题主要考查了勾股定理,根据坐标系中两点距离计算公式求解即可.
【详解】解:∵,
∴,
故答案为:.
16.等腰直角三角形
【分析】
本题考查了非负数的性质,勾股定理的逆运用,根据几个非负数的和等于0,则每一个算式都等于0,列式求出a、b,c的关系,即可得解.
【详解】解:根据题意得:,
,
的形状是等腰直角三角形.
故答案为:等腰直角三角形.
17.
【分析】本题主要考查了全等三角形的判定与性质、勾股定理等知识点,正确作出辅助线、构造全等三角形成为解题的关键.
如图:作交的延长线于点E,,再证可得,;再运用勾股定理可得,最后根据三角形的中线的定义即可解答.
【详解】解:作交的延长线于点E,,
∵是边上的中线,,
∴,
∵,
∴,
∴,,
∴,
∴,
∴,
∵
∴.
故答案为:.
18.
【分析】本题主要考查了勾股定理,平行线的性质.等腰三角形的判定和性质,图形的折叠问题.过点F作于点G,则,,根据平行线的性质乙折叠的性质可得,从而得到,设,则,在中,根据勾股定理可得,从而得到,再由勾股定理,即可求解.
【详解】解:如图,过点F作于点G,则,,
根据题意得:,
∴,
由折叠的性质得:,,
∴,
∴,
设,则,
在中,,
∴,
解得:,
∴,
∴,
∴.
故答案为:
19.12.5或5.5
【分析】本题考查了勾股定理,熟练掌握勾股定理是解题的关键.
分两种情况讨论:锐角三角形和钝角三角形,根据勾股定理求得,,再由图形求出,在锐角三角形中,,在钝角三角形中,.
【详解】解:分两种情况讨论:①如图1,锐角中,,,边上高,
在中,,,
由勾股定理得,
,
在中,,,
由勾股定理得,
,
的长为;
②如图2,钝角中,,,边上高,
在中,,,
由勾股定理得,
,
在中,,
由勾股定理得,
,
的长为.
故答案为:12.5或5.5.
20.22
【分析】过B作BE⊥AD于E,过C作CF⊥AD交DA的延长线于F,由∠BAC=90,AB=AC,得到∠EAB+∠FAC=∠EAB+∠EBA=90,证出∠ABE=∠FAC,推出△ABE≌△AFC,得到AE=CF,BE=AF,设AE=CF=x,AF=BE=DE=y,根据勾股定理得到CF=AE=,AF=BE=DE=3,AC= =2,于是得到S四边形ACBD=S△ABD+S△ABC=AD BE+AC AB=×4×3+×2×2=22.
【详解】解:过B作BE⊥AD于E,过C作CF⊥AD交DA的延长线于F,
∵∠BAC=90,AB=AC,
∴∠EAB+∠FAC=∠EAB+∠EBA=90,
∴∠ABE=∠FAC,
在△ABE与△CAF中, ,
∴△ABE≌△AFC,
∴AE=CF,BE=AF,
∵∠ADB=45,
∴DE=BE,
设AE=CF=x,AF=BE=DE=y,
在Rt△CDF中,DF2+CF2=CD2,
即:(x+2y)2+x2=102,
∵x+y=4,
∴x=,y=3,
∴CF=AE=,AF=BE=DE=3,
∴AC==2,
∴S四边形ACBD=S△ABD+S△ABC=AD BE+AC AB=×4×3+×2×2=22.
故答案为22.
【点睛】本题考查全等三角形的判定和性质,等腰直角三角形的性质,三角形的面积的求法,正确的作出辅助线构造全等三角形是解题关键.
21.△ABC的周长是6+2
【分析】根据等边三角形性质求出∠B=60°,求出∠C=30°,求出BC=4,根据勾股定理求出AC,相加即可求出答案.
【详解】解:∵△ABD是等边三角形,
∴∠B=60°,
∵∠BAC=90°,
∴∠C=180°﹣90°﹣60°=30°,
∴BC=2AB=4,
在Rt△ABC中,由勾股定理得:
AC=
=2,
∴△ABC的周长是AC+BC+AB=2+4+2=6+2.
答:△ABC的周长是6+2.
【点睛】本题考查了勾股定理,含30度角的直角三角形,等边三角形性质,三角形的内角和定理等知识点的应用,主要培养学生运用性质进行推理和计算的能力,此题综合性比较强,是一道比较好的题目.
22.(1)详见解析
(2)详见解析
(3)
【分析】(1)利用勾股定理求解即可;
(2)利用勾股定理求解即可;
(3)连接AC,证明△ABC是等腰直角三角形即可得到答案.
【详解】(1)解:如图所示,线段AB即为所求;
;
(2)解:如图所示,△ABC即为所求;
;
(3)解:如图3所示,连接AC,
∵,,,
∴,,
∴,
∴△ABC是等腰直角三角形,
∴.
【点睛】本题主要考查了勾股定理,勾股定理的逆定理,等腰直角三角形的性质与判定,熟知勾股定理与勾股定理的逆定理是解题的关键.
23.24 cm
【分析】连接AC,先根据勾股定理求出AC的长度,再根据勾股定理的逆定理判断出△ACD的形状,再利用三角形的面积公式求解即可.
【详解】如图,连接AC,
在Rt△ABC中,AB=4cm, BC=3cm,
AC= 5cm,
在△ACD中 ,CD=12cm, DA=13cm,
∴AC2 +CD2=AD2,
△ADC是直角三角形,∠ACD=90°,
S四边形ABCD=S△ADC-S△ABC,
S四边形ABCD = ×AC×CD-× AB×BC
= ×5×12- ×4×3
=24(cm ) .
【点睛】此题考查了勾股定理及逆定理,熟练掌握勾股定理及逆定理是解本题的关键.
24.
【分析】先根据矩形的性质得,,再根据折叠的性质可以得到,,,然后根据题目中的数据,即可得到的长,最后根据勾股定理即可求得和的长.
【详解】解:四边形是长方形,,
,
是翻折而成,
,,
∴是直角三角形,
,
在中,
设,
在中,,即,解得
【点睛】本题考查的是翻折变换、勾股定理,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.
25.(1)20海里;(2)当渔船继续航行20分钟才能与小岛C的距离最短.
【分析】(1)作BH⊥AC于H.首先证明AB=BC,AH=HC,在直角△ABH中利用勾股定理求出HA即可解决问题;
(2)作CK⊥AB交AB的延长线于K.求出BK即可解决问题;
【详解】(1)作BH⊥AC于H.
∵∠CBD=∠CAB+∠BCA,∠CAB=30°,∠CBD=60°,
∴∠ACB=∠BAC=30°
∴BA=BC=30×=20海里.
∵BH⊥AC,
∴BH=AB=10海里,
∴AH==10海里,
∴AC=2AH=20海里.
(2)作CK⊥AB交AB的延长线于K.
在Rt△BCK中,∠BCK=90°-∠CBK=30°,
BK= BC=10海里,
∴时间t=小时=20分钟.
∴当渔船继续航行20分钟才能与小岛C的距离最短.
【点睛】此题考查勾股定理的应用—方向角问题,解题关键在于结合航海中的实际问题,利用勾股定理和含有30°角的直角三角形性质是解决问题的关键.
26.(1);(2)
【分析】(1)根据旋转的性质,得到是等腰直角三角形,得到:利用勾股定理求出,再利用勾股定理逆定理得到,再利用,即可得解;
(2)将绕点逆时针旋转到的位置,连接;根据旋转的性质,得到是等边三角形,利用勾股定理逆定理,得到,利用,即可得解.
【详解】解:(1)如图1,由题意得:
;;
由勾股定理得:;
,,
,
,
,
.
(2)如图2,将绕点逆时针旋转到的位置,连接;
则,,;
为等边三角形,,;
,,
,
,,
.
【点睛】本题考查旋转的性质,等腰三角形的判定和性质,等边三角形的判定和性质,以及勾股定理逆定理.通过旋转,构造全等三角形,进而得到等腰三角形和直角三角形,是解题的关键.
27.(1)
(2)证明见解析
(3)或
【分析】(1)根据证明即可求证;
(2)根据点关于直线的对称点,等腰直角三角形的性质可证,可得,,再证明可得,在中,根据勾股定理即可求证;
(3)根据题意,结合图形,分类讨论:①如图所示,在延长线上时;②如图所示,在上,在点的左边时;根据(1),(2)的结论即可求证.
【详解】(1)解:,理由如下,
∵等腰直角三角形,,,
∴,
∵点关于直线的对称点,且,
∴,,则
∵,,
∴,
∴,
在中,
,
∴,
∴,,
∵,
∴,即,
故答案为:.
(2)证明:如图所示,
∵点关于直线的对称点,且,
∴,,
∴,
∵,,
∴,
在中,
,
∴,
∴,
∴,则,,
在中,
,
∴,
∴,
∴在中,,且,,
∴.
(3)解:①如图所示,在延长线上时,作关于对称点,连接,
∵在中,,,
∴,
∴,
由(2)知, ,,
设,则,
∴,
∴由(2)的结论可知,,即,解得,,
∴;
②如图所示,在上,在点的左边时,作关于对称点,连接,
同理,
∵,BD=,
∴,
由(1)知, ,设,则,,
∴,即,解得,,
∴,
∴,
∴;
综上所示,或.
【点睛】本题主要考查等腰直角三角形的性质,折叠的性质,全等三角形的判定和性质,勾股定理的综合,掌握以上知识的综合运用是解题的关键.
答案第1页,共2页
答案第1页,共2页
满分:120分 时间:90分钟
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题(共30分)
1.(本题3分)观察下列各组数:①7,12,15,②8,15,17,③7,24,25,④12,15,20,其中能作为直角三角形三边长的有( )
A.1组 B.2组 C.3组 D.4组
2.(本题3分)在中,、、的对应边分别是a、b、c,若,则下列等式中成立的是( )
A. B. C. D.
3.(本题3分)三角形的三边a,b,c满足,则此三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
4.(本题3分)如图,一棵树(树干与地面垂直)高米,在一次强台风中树被强风折断,倒下后的树顶C与树根A的距离为米,则这棵树断裂处点B离地面的高度的值为( )
A.2.4米 B.2.6米 C.0.6米 D.1米
(6) (7) (10)
5.(本题3分)一架5m的梯子,斜靠在一竖直的墙上,这时梯子的底端距墙角4m,若梯子的顶端下滑1m,则梯子的底端将滑动( )
A.0m B.1m C. D.
6.(本题3分)某酒店打算在一段楼梯面上铺上宽为2米的地毯,台阶的侧面如图所示,如果这种地毯每平方米售价为80元,则购买这种地毯至少需要( )
A.2560元 B.2620元 C.2720元 D.2840元
7.(本题3分)如图,在中,,,点在上,,,则的长为( )
A. B. C. D.
8.(本题3分)在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,下列说法错误的是( )
A.如果∠C-∠B=∠A,那么△ABC是直角三角形,且∠C=90°
B.如果c2=a2+b2,那么△ABC是直角三角形,且∠C=90°
C.如果,那么△ABC是直角三角形,且∠C=90°
D.如果∠A:∠B:∠C=5:2:3,那么△ABC是直角三角形 ,且∠A=90°
9.(本题3分)下列各命题的逆命题成立的是( )
A.全等三角形的对应角相等 B.若两数相等,则它们的绝对值相等
C.若两个角是45,那么这两个角相等 D.两直线平行,同位角相等
10.(本题3分)一只蚂蚁从圆柱体的下底面点沿着侧面爬到上底面点,已知圆柱的底面半径为,高为(取3),则蚂蚁所走过的最短路径是( )
A.8 B.9 C.10 D.12
评卷人得分
二、填空题(共30分)
11.(本题3分)如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形,,的面积依次为,,,则正方形的面积为 .
12.(本题3分)一艘轮船以的速度离开港口向东北方向航行,另一艘轮船同时离开港口以的速度向东南方向航行,它们离开港口半小时后相距 .
13.(本题3分)一个三角形的三边长度之比为15:8:17,则这个三角形的最大角是 度.
14.(本题3分)已知:在中,,,,则 .
15.(本题3分)在平面直角坐标系中,,则线段
16.(本题3分)已知a、b、c是的三边长,且满足关系,则的形状是 .
17.(本题3分)如图,在中,是边上的中线,,,,则的长为 .
(14) (17)
18.(本题3分)如图,是一张长方形纸片,.在边上取一点E,在上取一点F,将纸片沿折叠,点C恰好落在点A处,则线段的长度为 .
(20)
19.(本题3分)在中,,,高,则 .
20.(本题3分)已知:如图,等腰直角△ABC,∠BAC=90,AB=AC,点D为△ABC外一点,∠ADB=45,连接CD,AD=4,CD=10,则四边形ACBD的面积为
评卷人得分
三、问答题(共60分)
21.(本题6分)如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形.若AB=2,求△ABC的周长.(结果保留根号)
22.(本题7分)如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
(1)在图1中画一条长度为的线段,要求线段的端点在格点上;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2,,;
(3)如图3,点A,B,C是小正方形的顶点,求的度数.
23.(本题7分)如图,四边形ABCD中,,,,,,求四边形ABCD的面积.
24.(本题8分)如图所示,在长方形纸片中,已知,折叠纸片使边与对角线重合,点B落在点F处,折痕为,且,则求的长为多少?
25.(本题10分)如图,一艘渔船正以30海里/时的速度由西向东追赶鱼群,在A处看见小岛C在船的北偏东60°方向上,40分钟后,渔船行至B处,此时看见小岛C在渔船的北偏东30°方向上.
(1)求A处与小岛C之间的距离;
(2)渔船到达B处后,航行方向不变,当渔船继续航行多长时间时,才能与小岛C的距离最短.
26.(本题10分)(1)在一次数学探究活动中,陈老师给出了一道题.
如图1,已知中,,,是内的一点,且,,,求的度数.
小强在解决此题时,是将绕旋转到的位置(即过作,且使,连接、.你知道小强是怎么解决的吗?
(2)请根据(1)的思想解决以下问题:
如图2所示,设是等边内一点,,,,求的度数.
27.(本题12分)已知等腰直角三角形,,.点边上的一个动点(不与点重合),点在直线上,连接,且.
(1)若点线段上一点,如图1,作点关于直线的对称点,连接,则与的数量关系为 ;位置关系为 .
(2)若点是线段延长线上一点,如图2,作点于直线对称点,连接.求证:.
(3)如图3,若, ,求的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】本题考查了勾股定理的逆定理;熟练掌握勾股定理的逆定理,并能进行推理论证与计算是解决问题的关键.
由勾股定理的逆定理得出②③能构成直角三角形,①④不能构成直角三角形;即可得出结论.
【详解】解:,
∴7,12,15不能构成直角三角形,
∴①不能作为直角三角形三边长;
∵,
∴8,15,17能构成直角三角形,
∴②能作为直角三角形三边长;
,
∴7,24,25能构成直角三角形,
∴③能作为直角三角形三边长;
,
∴12,15,20不能构成直角三角形,
∴④不能作为直角三角形三边长;
∴能作为直角三角形三边长的有2组,
故选:B.
2.C
【分析】由已知两角之和为90度,利用三角形内角和定理得到三角形为直角三角形,利用勾股定理即可得到结果.
【详解】解:∵在中,,
∴,
∴为直角三角形,
则根据勾股定理得:.
故选:C.
【点睛】此题考查了勾股定理,熟练掌握勾股定理是解题的关键.
3.B
【分析】
本题考查了勾股定理的逆定理.先根据完全平方公式对已知等式进行化简,再根据勾股定理的逆定理进行判定.
【详解】
解:∵,
∴,
∴,
∴三角形是直角三角形.
故选:B.
4.D
【分析】设这棵树断裂处点B离地面的高度的值为,则,然后根据勾股定理列方程求解即可.
【详解】解:设这棵树断裂处点B离地面的高度的值为x,则、,
∵是直角三角形,
∴,即,解得:,即.
故选:D.
【点睛】本题主要考查的是勾股定理的应用,根据勾股定理列出方程是解题关键.
5.D
【分析】本题考查了勾股定理的应用.由题意画出图形,由勾股定理求出,则,再由勾股定理求出的长,即可解决问题.
【详解】解:由题意画出图形如下:
在中,,,
,
在中,,,
,
,
即梯子的底端将滑动,
故选:D.
6.C
【分析】根据题意,结合图形,先把楼梯的横竖向上向左平移,构成一个矩形,再求得其面积,则购买地毯的钱数可求.
【详解】
利用平移线段,把楼梯的横竖向上向左平移,构成一个矩形,长宽分别为米、5米,
∴地毯的长度为12+5=17米,地毯的面积为17×2=34平方米,
∴购买这种地毯至少需要80×34=2720元.
故选C.
【点睛】本题考查的知识点是勾股定理的应用,生活中的平移现象,解题关键是要注意利用平移的知识,把要求的所有线段平移到一条直线上进行计算.
7.D
【分析】由勾股定理求出CD=1,再根据∠ADC是△ABD的外角,证出∠B=∠BAD,从而有BD=AD,即可求出BC的长.
【详解】解:在Rt△ACD中,由勾股定理得:
CD= =1,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD,
∵∠ADC=2∠B,
∴∠B=∠BAD,
∴BD=AD=,
∴BC=+1.
故选:D.
【点睛】本题主要考查了勾股定理、三角形外角的性质、等腰三角形的判定等知识,利用外角证出∠B=∠BAD是解题的关键.
8.C
【分析】根据直角三角形的定义,勾股定理以及三角形的内角和进行判断即可.
【详解】解:A.因为∠C﹣∠B=∠A,∠C+∠B+∠A=180°,所以2∠C=180°,即∠C=90°.故选项正确;
B.因为,则△ABC是直角三角形,且∠C=90°,故该选项正确;
C.因为,所以,则△ABC是直角三角形,且∠B=90°.故选项错误;
D.因为∠A:∠B:∠C=5:2:3,所以∠A=90°,∠B=36°,∠C=54°,则△ABC是直角三角形,且∠A=90°.故选项正确.
故选:C.
【点睛】本题主要考查了直角三角形的定义,熟练掌握直角三角形的定义以及勾股定理的逆定理是解题的关键.
9.D
【分析】先分别写出四个命题的逆命题,根据三角形全等的判定方法对A的逆命题进行判断;根据相反数的绝对值相等对B的逆命题进行判断;根据两个角相等,这两个角可为任意角度可对C的逆命题进行判断;根据平行线的判定定理对D的逆命题进行判断.
【详解】A. “全等三角形的对应角相等”的逆命题为“对应角相等的两三角形全等”,此逆命题为假命题,所以A选项错误;
B. “若两数相等,则它们的绝对值相等”的逆命题为“若两数的绝对值相等,则这两数相等”,此逆命题为假命题,所以B选项错误;
C. “若两个角是45°,那么这两个角相等”的逆命题为“若两个角相等,你们这两个角是45°”,此逆命题为假命题,所以C选项错误;
D. “两直线平行,同位角相等”的逆命题为“同位角相等,两直线平行”,此逆命题为真命题,所以D选项正确.
故选D.
【点睛】此题考查命题与定理,解题关键在于掌握掌握各性质定义.
10.C
【分析】要求最短路径,首先要把圆柱的侧面展开,利用两点之间线段最短,然后利用勾股定理即可求解.
【详解】解:把圆柱侧面展开,展开图如图所示,点、的最短距离为线段的长.
在中,,,为底面半圆弧长,
,
所以.
故选:C.
【点睛】本题考查了平面展开-最短路径问题,解题的关键是会将圆柱的侧面展开,并利用勾股定理解答.
11.
【分析】本题考查的是勾股定理,根据勾股定理可得正方形A、B的面积之和等于正方形E的面积,正方形C、E的面积之和等于正方形D的面积,即可得到结果.
【详解】
由题意得,正方形的面积为,
则正方形的面积.
故答案为:.
12.26
【分析】先算出它们离开港口半小时后各自航行的路程,再根据勾股定理求解即可.
【详解】解:由题意可知,两艘轮船航行的路线成垂直关系,
它们离开港口半小时后各自航行的路程分别为、,
∴它们离开港口半小时后相距,
故答案为:26.
【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.
13.90
【分析】一个三角形的三边符合a2+b2=c2,根据勾股定理的逆定理,这个三角形是直角三角形.
【详解】解:设三角形的三边分别为8x,15x,17x,
∵(8x)2+(15x)2=(17x)2,
根据勾股定理的逆定理,这个三角形是直角三角形,最大角是90°.
故答案为:90.
【点睛】本题考查了勾股定理的逆定理:已知三角形ABC的三边满足a2+b2=c2,则三角形ABC是直角三角形.
14.
【分析】本题主要考查了勾股定理,含30度角的直角三角形的性质,过点A作交延长线于H,利用平角的定义和三角形内角和定理求出,则,,利用勾股定理得到,代值计算即可.
【详解】解:如图所示,过点A作交延长线于H,
∵,
∴,
∴,
∴,
∴,
在中,由勾股定理得,
在中,由勾股定理得,
∴,即,
∴(负值舍去),
故答案为:.
15.
【分析】本题主要考查了勾股定理,根据坐标系中两点距离计算公式求解即可.
【详解】解:∵,
∴,
故答案为:.
16.等腰直角三角形
【分析】
本题考查了非负数的性质,勾股定理的逆运用,根据几个非负数的和等于0,则每一个算式都等于0,列式求出a、b,c的关系,即可得解.
【详解】解:根据题意得:,
,
的形状是等腰直角三角形.
故答案为:等腰直角三角形.
17.
【分析】本题主要考查了全等三角形的判定与性质、勾股定理等知识点,正确作出辅助线、构造全等三角形成为解题的关键.
如图:作交的延长线于点E,,再证可得,;再运用勾股定理可得,最后根据三角形的中线的定义即可解答.
【详解】解:作交的延长线于点E,,
∵是边上的中线,,
∴,
∵,
∴,
∴,,
∴,
∴,
∴,
∵
∴.
故答案为:.
18.
【分析】本题主要考查了勾股定理,平行线的性质.等腰三角形的判定和性质,图形的折叠问题.过点F作于点G,则,,根据平行线的性质乙折叠的性质可得,从而得到,设,则,在中,根据勾股定理可得,从而得到,再由勾股定理,即可求解.
【详解】解:如图,过点F作于点G,则,,
根据题意得:,
∴,
由折叠的性质得:,,
∴,
∴,
设,则,
在中,,
∴,
解得:,
∴,
∴,
∴.
故答案为:
19.12.5或5.5
【分析】本题考查了勾股定理,熟练掌握勾股定理是解题的关键.
分两种情况讨论:锐角三角形和钝角三角形,根据勾股定理求得,,再由图形求出,在锐角三角形中,,在钝角三角形中,.
【详解】解:分两种情况讨论:①如图1,锐角中,,,边上高,
在中,,,
由勾股定理得,
,
在中,,,
由勾股定理得,
,
的长为;
②如图2,钝角中,,,边上高,
在中,,,
由勾股定理得,
,
在中,,
由勾股定理得,
,
的长为.
故答案为:12.5或5.5.
20.22
【分析】过B作BE⊥AD于E,过C作CF⊥AD交DA的延长线于F,由∠BAC=90,AB=AC,得到∠EAB+∠FAC=∠EAB+∠EBA=90,证出∠ABE=∠FAC,推出△ABE≌△AFC,得到AE=CF,BE=AF,设AE=CF=x,AF=BE=DE=y,根据勾股定理得到CF=AE=,AF=BE=DE=3,AC= =2,于是得到S四边形ACBD=S△ABD+S△ABC=AD BE+AC AB=×4×3+×2×2=22.
【详解】解:过B作BE⊥AD于E,过C作CF⊥AD交DA的延长线于F,
∵∠BAC=90,AB=AC,
∴∠EAB+∠FAC=∠EAB+∠EBA=90,
∴∠ABE=∠FAC,
在△ABE与△CAF中, ,
∴△ABE≌△AFC,
∴AE=CF,BE=AF,
∵∠ADB=45,
∴DE=BE,
设AE=CF=x,AF=BE=DE=y,
在Rt△CDF中,DF2+CF2=CD2,
即:(x+2y)2+x2=102,
∵x+y=4,
∴x=,y=3,
∴CF=AE=,AF=BE=DE=3,
∴AC==2,
∴S四边形ACBD=S△ABD+S△ABC=AD BE+AC AB=×4×3+×2×2=22.
故答案为22.
【点睛】本题考查全等三角形的判定和性质,等腰直角三角形的性质,三角形的面积的求法,正确的作出辅助线构造全等三角形是解题关键.
21.△ABC的周长是6+2
【分析】根据等边三角形性质求出∠B=60°,求出∠C=30°,求出BC=4,根据勾股定理求出AC,相加即可求出答案.
【详解】解:∵△ABD是等边三角形,
∴∠B=60°,
∵∠BAC=90°,
∴∠C=180°﹣90°﹣60°=30°,
∴BC=2AB=4,
在Rt△ABC中,由勾股定理得:
AC=
=2,
∴△ABC的周长是AC+BC+AB=2+4+2=6+2.
答:△ABC的周长是6+2.
【点睛】本题考查了勾股定理,含30度角的直角三角形,等边三角形性质,三角形的内角和定理等知识点的应用,主要培养学生运用性质进行推理和计算的能力,此题综合性比较强,是一道比较好的题目.
22.(1)详见解析
(2)详见解析
(3)
【分析】(1)利用勾股定理求解即可;
(2)利用勾股定理求解即可;
(3)连接AC,证明△ABC是等腰直角三角形即可得到答案.
【详解】(1)解:如图所示,线段AB即为所求;
;
(2)解:如图所示,△ABC即为所求;
;
(3)解:如图3所示,连接AC,
∵,,,
∴,,
∴,
∴△ABC是等腰直角三角形,
∴.
【点睛】本题主要考查了勾股定理,勾股定理的逆定理,等腰直角三角形的性质与判定,熟知勾股定理与勾股定理的逆定理是解题的关键.
23.24 cm
【分析】连接AC,先根据勾股定理求出AC的长度,再根据勾股定理的逆定理判断出△ACD的形状,再利用三角形的面积公式求解即可.
【详解】如图,连接AC,
在Rt△ABC中,AB=4cm, BC=3cm,
AC= 5cm,
在△ACD中 ,CD=12cm, DA=13cm,
∴AC2 +CD2=AD2,
△ADC是直角三角形,∠ACD=90°,
S四边形ABCD=S△ADC-S△ABC,
S四边形ABCD = ×AC×CD-× AB×BC
= ×5×12- ×4×3
=24(cm ) .
【点睛】此题考查了勾股定理及逆定理,熟练掌握勾股定理及逆定理是解本题的关键.
24.
【分析】先根据矩形的性质得,,再根据折叠的性质可以得到,,,然后根据题目中的数据,即可得到的长,最后根据勾股定理即可求得和的长.
【详解】解:四边形是长方形,,
,
是翻折而成,
,,
∴是直角三角形,
,
在中,
设,
在中,,即,解得
【点睛】本题考查的是翻折变换、勾股定理,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.
25.(1)20海里;(2)当渔船继续航行20分钟才能与小岛C的距离最短.
【分析】(1)作BH⊥AC于H.首先证明AB=BC,AH=HC,在直角△ABH中利用勾股定理求出HA即可解决问题;
(2)作CK⊥AB交AB的延长线于K.求出BK即可解决问题;
【详解】(1)作BH⊥AC于H.
∵∠CBD=∠CAB+∠BCA,∠CAB=30°,∠CBD=60°,
∴∠ACB=∠BAC=30°
∴BA=BC=30×=20海里.
∵BH⊥AC,
∴BH=AB=10海里,
∴AH==10海里,
∴AC=2AH=20海里.
(2)作CK⊥AB交AB的延长线于K.
在Rt△BCK中,∠BCK=90°-∠CBK=30°,
BK= BC=10海里,
∴时间t=小时=20分钟.
∴当渔船继续航行20分钟才能与小岛C的距离最短.
【点睛】此题考查勾股定理的应用—方向角问题,解题关键在于结合航海中的实际问题,利用勾股定理和含有30°角的直角三角形性质是解决问题的关键.
26.(1);(2)
【分析】(1)根据旋转的性质,得到是等腰直角三角形,得到:利用勾股定理求出,再利用勾股定理逆定理得到,再利用,即可得解;
(2)将绕点逆时针旋转到的位置,连接;根据旋转的性质,得到是等边三角形,利用勾股定理逆定理,得到,利用,即可得解.
【详解】解:(1)如图1,由题意得:
;;
由勾股定理得:;
,,
,
,
,
.
(2)如图2,将绕点逆时针旋转到的位置,连接;
则,,;
为等边三角形,,;
,,
,
,,
.
【点睛】本题考查旋转的性质,等腰三角形的判定和性质,等边三角形的判定和性质,以及勾股定理逆定理.通过旋转,构造全等三角形,进而得到等腰三角形和直角三角形,是解题的关键.
27.(1)
(2)证明见解析
(3)或
【分析】(1)根据证明即可求证;
(2)根据点关于直线的对称点,等腰直角三角形的性质可证,可得,,再证明可得,在中,根据勾股定理即可求证;
(3)根据题意,结合图形,分类讨论:①如图所示,在延长线上时;②如图所示,在上,在点的左边时;根据(1),(2)的结论即可求证.
【详解】(1)解:,理由如下,
∵等腰直角三角形,,,
∴,
∵点关于直线的对称点,且,
∴,,则
∵,,
∴,
∴,
在中,
,
∴,
∴,,
∵,
∴,即,
故答案为:.
(2)证明:如图所示,
∵点关于直线的对称点,且,
∴,,
∴,
∵,,
∴,
在中,
,
∴,
∴,
∴,则,,
在中,
,
∴,
∴,
∴在中,,且,,
∴.
(3)解:①如图所示,在延长线上时,作关于对称点,连接,
∵在中,,,
∴,
∴,
由(2)知, ,,
设,则,
∴,
∴由(2)的结论可知,,即,解得,,
∴;
②如图所示,在上,在点的左边时,作关于对称点,连接,
同理,
∵,BD=,
∴,
由(1)知, ,设,则,,
∴,即,解得,,
∴,
∴,
∴;
综上所示,或.
【点睛】本题主要考查等腰直角三角形的性质,折叠的性质,全等三角形的判定和性质,勾股定理的综合,掌握以上知识的综合运用是解题的关键.
答案第1页,共2页
答案第1页,共2页
