数学人教A版(2019)必修第一册5.4.1正弦函数与余弦函数的图像 课件(共26张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.4.1正弦函数与余弦函数的图像 课件(共26张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-03 06:25:32 | ||
图片预览







文档简介
(共26张PPT)
5.4.1正弦函数、余弦函数的图象
1. 了解利用单位圆正弦函数的概念画正弦曲线的方法.
2.掌握“五点法”画正弦曲线和余弦曲线的步骤与方法,能利用“五点法”画出简单的正弦、余弦函数图象.(重点、难点)
3.理解正弦曲线与余弦曲线之间的联系(难点)
学习目标
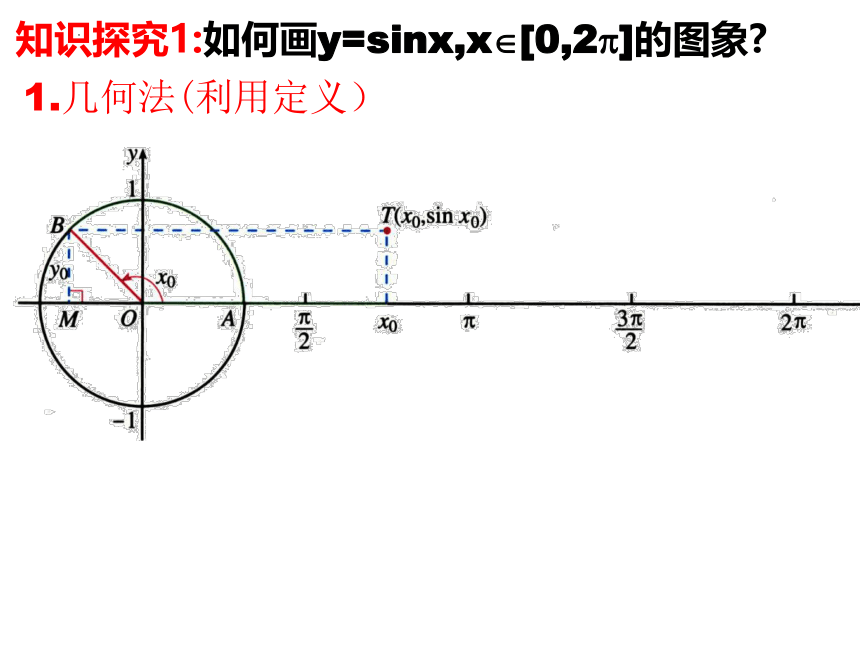
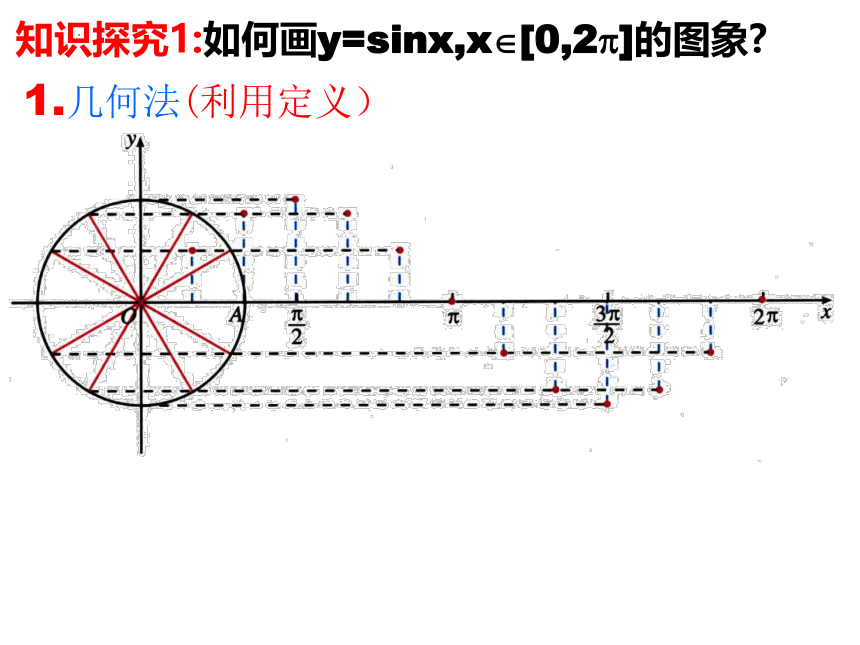
知识探究1:如何画y=sinx,x [0,2 ]的图象
1.几何法(利用定义)
知识探究1:如何画y=sinx,x [0,2 ]的图象
1.几何法(利用定义)
知识探究1:如何画y=sinx,x [0,2 ]的图象
1.几何法(利用定义)
1
-1
0
y
x
●
●
●
●
●
●
●
●
●
●
●
●
●
描图:用光滑曲线将这些正弦线的终点连结起来.
将图象左、右平移(每次2π个单位)
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
正弦曲线
知识探究2:如何画y=cosx,x [0,2 ]的图象
方法1:利用正弦函数平移
余弦函数的图象
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
正弦函数的图象
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=cosx与 y=sin(x+ ), x R图象相同
余弦曲线
正弦曲线
形状完全一样只是位置不同
练习.下列叙述:
①作正弦函数的图象时,单位圆的半径长与x轴的单位长度必须一致;
②y=sinx,x∈[0,2π]的图象关于点P(π,0)中心对称;
③y=cosx,x∈[0,2π]的图象关于直线x=π成轴对称图形;
④正、余弦函数y=sinx和y=cosx的图象不超出直线y=-1与y=1所夹的区域,其中正确的是 .
①②③④
问题1:在精确度要求不太高时,如何快捷地作出正(余)弦函数的图象呢
2.在作出正弦函数的图象时,应抓住哪些关键点
与x轴的交点
图象的最高点
图象的最低点
与x轴的交点
图象的最高点
图象的最低点
五点作图法
图象中关键点
正弦函数的图象
余弦函数的图象
例1.画出下列函数的简图
(1)y =-sin x, x∈[0,2π]
(2)y =1+cos x, x∈[0,2π]
典例分析及格式规范:
x
sinx
-sinx
解:(1)按五个关键点列表:
0
0
0
1
-1
0
1
-1
1
0
x
●
●
●
●
●
五点法作图
(2)描点
(1)列表
(3)连线
0
y
-1
1
(1)y =-sin x, x∈[0,2π]
(2)按五个关键点列表:
1
-1
1
0
0
1
-1
0
0
-1
x
cosx
1+cosx
(2)y =1+cos x, x∈[0,2π]
o
-1
1
2
y
x
y
x
o
-1
1
y=-sinx,x∈[0,2π]
y=sinx,x∈[0,2π]
y=cosx,x∈[0,2π]
y=1+cosx,x∈[0,2π]
1.函数y=1+cosx的图象与函数y=cosx的图象有什么关系
2.函数y=-sinx的图象与函数y=sinx的图象有什么关系
左+右-
巩固练习:
1.分别作出下列函数简图(五点法作图).
(1)y=2sinx,x∈[0,2π].
(2)y=sin2x,x∈[0,π].
y=1-cosx,x∈[0,2π].
①列表
②描点作图
解:(1)y=2sinx,x∈[0,2π]
x
0 2
0 2 0 -2 0
y
2
x
O
y=2sinx,x∈[0,2π]
y=2sinx
1
-1
-2
0
0 2
2x
0 1 0 -1 0
y
1
O
y=sin2x,x∈[0,π]
y=sin2x
-1
解:(2)y=sin2x,x∈[0,2π]
①列表
②描点作图
C
x
y
O
2π
π
1
-1
应用一:利用正、余弦函数的图象解三角不等式
x
-1
O
2π
π
1
y
数形结合
利用正、余弦函数图象研究图象的交点
[例3](1)方程x2-cos x=0的实数解的个数是______;
(2)方程sin x=lg x的解的个数是________.
3.函数f(x)=sin x+2|sin x|,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点,求k的取值范围.
(1,3)
变式
1.知识清单:(1)正弦函数图象的几何作图法.
(2)五点法作正弦函数图象.
(3)平移正弦曲线法和五点法作余弦函数图象.
(4)正弦函数、余弦函数图象的应用.
2.方法归纳:几何作图法、五点作图法、转化与化归.
3.常见误区:作简图时五点选取错误,作图不准确.
作业:课时作业(五十四)
5.4.1正弦函数、余弦函数的图象
1. 了解利用单位圆正弦函数的概念画正弦曲线的方法.
2.掌握“五点法”画正弦曲线和余弦曲线的步骤与方法,能利用“五点法”画出简单的正弦、余弦函数图象.(重点、难点)
3.理解正弦曲线与余弦曲线之间的联系(难点)
学习目标
知识探究1:如何画y=sinx,x [0,2 ]的图象
1.几何法(利用定义)
知识探究1:如何画y=sinx,x [0,2 ]的图象
1.几何法(利用定义)
知识探究1:如何画y=sinx,x [0,2 ]的图象
1.几何法(利用定义)
1
-1
0
y
x
●
●
●
●
●
●
●
●
●
●
●
●
●
描图:用光滑曲线将这些正弦线的终点连结起来.
将图象左、右平移(每次2π个单位)
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
正弦曲线
知识探究2:如何画y=cosx,x [0,2 ]的图象
方法1:利用正弦函数平移
余弦函数的图象
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
正弦函数的图象
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=cosx与 y=sin(x+ ), x R图象相同
余弦曲线
正弦曲线
形状完全一样只是位置不同
练习.下列叙述:
①作正弦函数的图象时,单位圆的半径长与x轴的单位长度必须一致;
②y=sinx,x∈[0,2π]的图象关于点P(π,0)中心对称;
③y=cosx,x∈[0,2π]的图象关于直线x=π成轴对称图形;
④正、余弦函数y=sinx和y=cosx的图象不超出直线y=-1与y=1所夹的区域,其中正确的是 .
①②③④
问题1:在精确度要求不太高时,如何快捷地作出正(余)弦函数的图象呢
2.在作出正弦函数的图象时,应抓住哪些关键点
与x轴的交点
图象的最高点
图象的最低点
与x轴的交点
图象的最高点
图象的最低点
五点作图法
图象中关键点
正弦函数的图象
余弦函数的图象
例1.画出下列函数的简图
(1)y =-sin x, x∈[0,2π]
(2)y =1+cos x, x∈[0,2π]
典例分析及格式规范:
x
sinx
-sinx
解:(1)按五个关键点列表:
0
0
0
1
-1
0
1
-1
1
0
x
●
●
●
●
●
五点法作图
(2)描点
(1)列表
(3)连线
0
y
-1
1
(1)y =-sin x, x∈[0,2π]
(2)按五个关键点列表:
1
-1
1
0
0
1
-1
0
0
-1
x
cosx
1+cosx
(2)y =1+cos x, x∈[0,2π]
o
-1
1
2
y
x
y
x
o
-1
1
y=-sinx,x∈[0,2π]
y=sinx,x∈[0,2π]
y=cosx,x∈[0,2π]
y=1+cosx,x∈[0,2π]
1.函数y=1+cosx的图象与函数y=cosx的图象有什么关系
2.函数y=-sinx的图象与函数y=sinx的图象有什么关系
左+右-
巩固练习:
1.分别作出下列函数简图(五点法作图).
(1)y=2sinx,x∈[0,2π].
(2)y=sin2x,x∈[0,π].
y=1-cosx,x∈[0,2π].
①列表
②描点作图
解:(1)y=2sinx,x∈[0,2π]
x
0 2
0 2 0 -2 0
y
2
x
O
y=2sinx,x∈[0,2π]
y=2sinx
1
-1
-2
0
0 2
2x
0 1 0 -1 0
y
1
O
y=sin2x,x∈[0,π]
y=sin2x
-1
解:(2)y=sin2x,x∈[0,2π]
①列表
②描点作图
C
x
y
O
2π
π
1
-1
应用一:利用正、余弦函数的图象解三角不等式
x
-1
O
2π
π
1
y
数形结合
利用正、余弦函数图象研究图象的交点
[例3](1)方程x2-cos x=0的实数解的个数是______;
(2)方程sin x=lg x的解的个数是________.
3.函数f(x)=sin x+2|sin x|,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点,求k的取值范围.
(1,3)
变式
1.知识清单:(1)正弦函数图象的几何作图法.
(2)五点法作正弦函数图象.
(3)平移正弦曲线法和五点法作余弦函数图象.
(4)正弦函数、余弦函数图象的应用.
2.方法归纳:几何作图法、五点作图法、转化与化归.
3.常见误区:作简图时五点选取错误,作图不准确.
作业:课时作业(五十四)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
