人教版八年级数学上册 第12章 12.1全等三角形 课件(共35张PPT)
文档属性
| 名称 | 人教版八年级数学上册 第12章 12.1全等三角形 课件(共35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-10 00:00:00 | ||
图片预览







文档简介
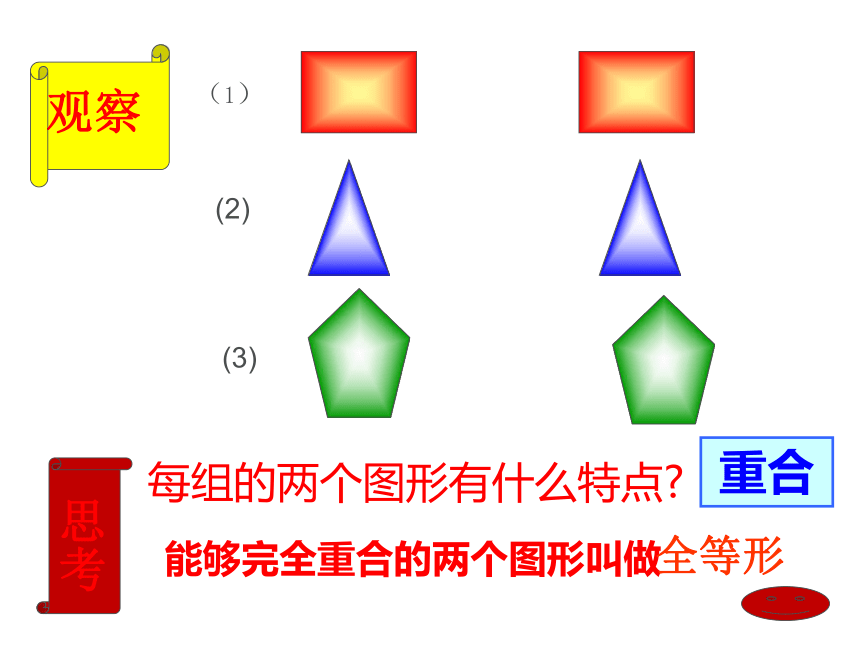
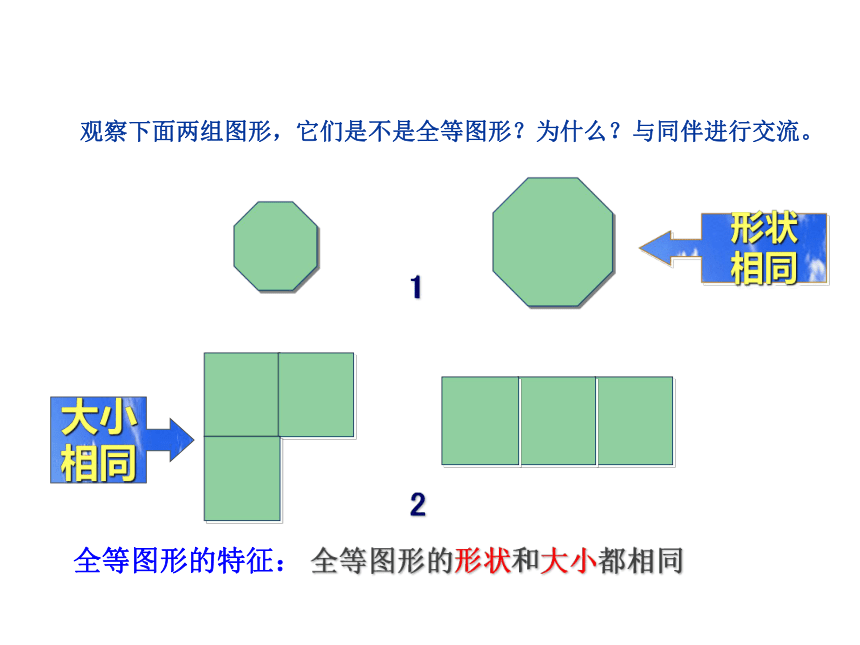
课件35张PPT。 全等三角形(1)(2)(3) 思考每组的两个图形有什么特点?观察重合能够完全重合的两个图形叫做全等形形状
相同大小
相同全等图形的特征:
全等图形的形状和大小都相同
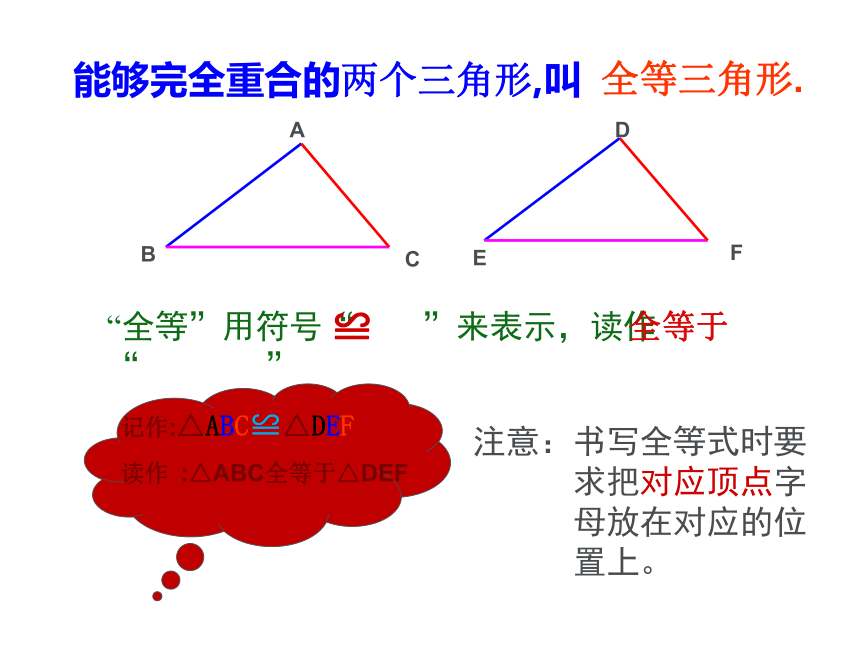
同一张底片洗出的照片是能够完全重合的全等形包括规则图形和不规则图形全等能够完全重合的两个三角形,叫全等三角形.注意:书写全等式时要
求把对应顶点字
母放在对应的位
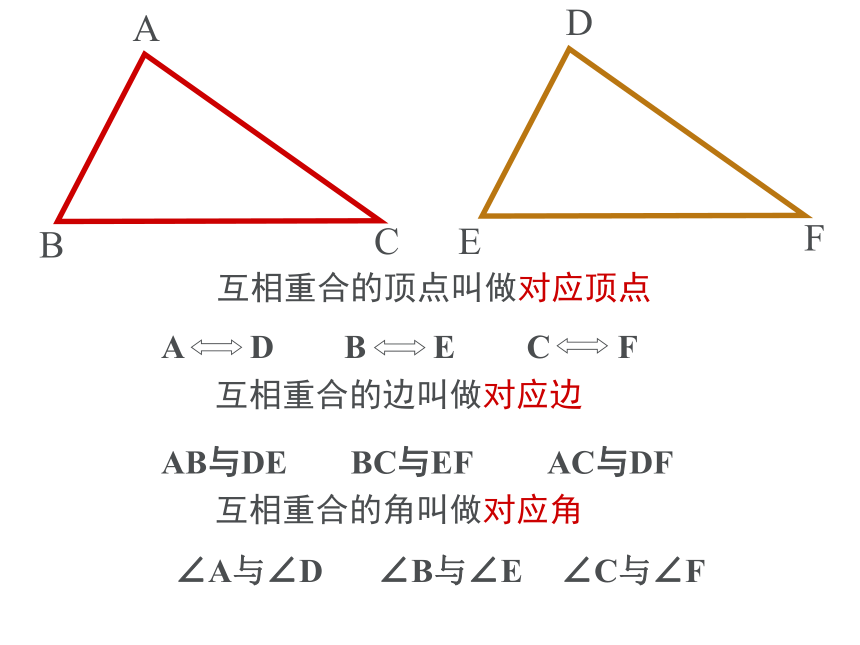
置上。“全等”用符号“ ”来表示,读作“ ”≌全等于ABCDEF互相重合的边叫做对应边互相重合的顶点叫做对应顶点互相重合的角叫做对应角AB与DEBC与EFAC与DF∠A与∠D∠B与∠E∠C与∠F(全等三角形的对应角相等)ABCDEF1、全等三角形的对应边相等,2、全等三角形的对应角相等。(已知)(全等三角形的对应边相等) ∴ AB=DE,BC=EF,AC=DF∠A=∠D,∠B=∠E,∠C=∠F全等三角形的性质:∵△ABC≌△DEFABCDEF∵△ABC≌△DEF
∴AB=DE,BC=EF,AC=DF.∴∠A= ∠D,∠B= ∠E,∠C= ∠F.ABCD∵△ABC≌△ABD∴AB=AB,BC=BD,AC=AD.∴∠BAC=∠BAD,∠ABC=∠ABD
∠C= ∠D.规律一:有公共边的,公共边是对应边ACODB∵△AOC≌△BOD∴AO=BO,AC=BD,OC=OD.∴∠A=∠B,∠C=∠D,
∠AOC= ∠BOD.规律二:有对顶角的,对顶角是对应角ABCDE∵△ABC≌△ADE∴AB=AD,AC=AE,BC=DE∴∠A=∠A,∠B=∠D,
∠ACB= ∠AED.规律三:有公共角的,公共角是对应角
ABCDE∵△ABC≌△DEC∴AB=DE,AC=DC,
BC=EC∴∠A=∠D,
∠B=∠E,
∠ACB= ∠DCE.规律四:一对最长的边是对应边
一对最短的边是对应边∵△ABC≌△FDE∴AB=FD,AC=FE,
BC=DE∴∠A=∠F,
∠B=∠D,
∠ACB= ∠FED.规律五:一对最大的角是对应角
一对最小的角是对应角已知△A0B≌△COD 指出图中两三角形的对应边和对应角已知△ABC≌△DCB 指出图中两三角形的对应边和对应角
找一找:请指出下列全等三角形的对应边和对应角1、 △ ABE ≌ △ ACF对应角是: ∠A和∠A、 ∠ABE和∠ACF、 ∠AEB和∠AFC;对应边是AB和AC、AE和AF、BE和CF。2、 △ BCE ≌ △ CBF对应角是: ∠BCE和 ∠CBF、 ∠BEC和∠CFB、 ∠CBE和 ∠BCF。对应边是:CB和BC、CE和BF、CF和BE。3、 △ BOF ≌ △ COE对应角是: ∠BOF和∠COE、 ∠BFO 和∠CEO、 ∠ FOB和∠EOC。对应边是:OF和OE、OB和OC、BF和CE。典型例题例1若ΔDEF≌ΔABC, ∠A=70°,∠B=50°,点A的对应点是点D,AB=DE,那么∠F的度数等于( )A.50° B.60° C.50° D.以上都不对分析: 由∠A=70°,∠B=50°知道:∠C=60°,所以ΔABC是不等边三角形,由点A的对应点是点D,AB=DE知道:∠F的对应角是∠C(60°)B典型例题例2如图,若ΔOAD≌ΔOBC, 且∠O=65°,∠C=20°,则∠OAD= .分析:由∠O=65°,∠C=20°知道, ∠OBC=95 °, 由ΔOAD≌ΔOBC知: ∠OAD=95 °。95 °典型例题例3:如图,若ΔABC≌ΔAEF, AB=AE,∠B=∠E,则下列结论:①AC=AF, ②∠FAB=∠EAB, ③EF=BC,④ ∠FAC=∠EAB,其中正确结论的个数是( ) A.1个 B.2个 C.3个 D.4个分析:由ΔABC≌ΔAEF和 ∠B=∠E知:AC=AF.所以①是正确的。①AC=AF,A典型例题例3:如图,若ΔABC≌ΔAEF, AB=AE,∠B=∠E,则下列结论:①AC=AF, ②∠FAB=∠EAB, ③EF=BC,④ ∠FAC=∠EAB,其中正确结论的个数是( ) A.1个 B.2个 C.3个 D.4个分析:由AB=AE和①AC=AF知: EF=BC ,所以③是正确的。③EF=BC典型例题例3:如图,若ΔABC≌ΔAEF, AB=AE,∠B=∠E,则下列结论:①AC=AF, ②∠FAB=∠EAB, ③EF=BC,④ ∠FAC=∠EAB,其中正确结论的个数是( ) A.1个 B.2个 C.3个 D.4个分析:由③EF=BC知: ∠BAC =∠EAF,得④ ∠FAC=∠EAB ,所以④是正确的。④ ∠FAC=∠EAB典型例题例3:如图,若ΔABC≌ΔAEF, AB=AE,∠B=∠E,则下列结论:①AC=AF, ②∠FAB=∠EAB, ③EF=BC,④ ∠FAC=∠EAB,其中正确结论的个数是( ) A.1个 B.2个 C.3个 D.4个分析:因为④∠FAC=∠EAB ,要使②∠FAB=∠EAB正确,必须有∠FAC= ∠FAB,而AF并不是角平分线,所以②不正确。C典型例题例4:如图,已知ΔABC≌ΔFED, BC=ED, 求证:AB∥EF证明: ∵ΔABC≌ΔFED, BC=ED ∴BC与ED是对应边
∴∠ =∠ , ( ) ∴ AB∥EF将上述证明过程补充完整.AF全等三角形的对应角相等典型例题例5:如图,已知ΔABD≌ΔAEC, ∠B和∠E,是对应角,AB与AE是对应边,试说明:BC=DE.分析: 因为ΔABD≌ΔAEC并且∠B和∠E是对应角,所以AD和AC是对应边,又因为AB与AE是对应边,所以BD和EC是对应边,即BD=EC,所以BD-CD=EC-CD,所以BC=DE.典型例题例6:如图,已知ΔAEF是ΔABC绕A点顺时针旋转55°得到的,求∠BAE,∠CAF和∠BME的度数.解:因为AE和AF分别是AB和AC旋转后的位置,所以∠BAE=∠CAF= 55°;又因为ΔAEF≌ΔABC,所以∠B=∠E, 因为∠ANB和∠ENM是对顶角,所以∠BME= ∠BAE= 55°;∠A+∠B=∠C+∠D典型例题例7:如图,已知ΔABE≌ΔACD,且∠1=∠2, ∠B=∠C,请指出其余的对应边和对应角.分析:由ΔABE≌ΔACD以及∠1=∠2, ∠B=∠C知:∠ BAE与∠CAD是对应角,根据“对应角的对边是对应边 ”可知:AD与AE,AE与AD,BE与CD分别是对应边.2. 叫做全等三角形。 1.能够重合的两个图形叫做 。全等形4.全等三角形的 和 相等对应边对应角对应顶点课 堂 小 结 能够重合的两个三角形3.“全等”用符号“ ”来表示,读作“ ”对应边对应角5.书写全等式时要求把对应字母放在对应
的位置上全等于≌ 其中:互相重合的顶点叫做___互相重合的边叫做____互相重合的角叫做___小结寻找对应元素的规律(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边,
最小的边是对应边;
(5)两个全等三角形最大的角是对应角,
最小的角是对应角;
思考一: 若你手上有一张长方形纸片,如何是长方形变成两个最大的全等三角形,而总面积又没有 变化?思考二:拓展与延伸 下图是一个等边三角形,你能把它分成两个全等三角形吗?你能把它分成三个全等三角形吗?四个呢? 再 见
相同大小
相同全等图形的特征:
全等图形的形状和大小都相同
同一张底片洗出的照片是能够完全重合的全等形包括规则图形和不规则图形全等能够完全重合的两个三角形,叫全等三角形.注意:书写全等式时要
求把对应顶点字
母放在对应的位
置上。“全等”用符号“ ”来表示,读作“ ”≌全等于ABCDEF互相重合的边叫做对应边互相重合的顶点叫做对应顶点互相重合的角叫做对应角AB与DEBC与EFAC与DF∠A与∠D∠B与∠E∠C与∠F(全等三角形的对应角相等)ABCDEF1、全等三角形的对应边相等,2、全等三角形的对应角相等。(已知)(全等三角形的对应边相等) ∴ AB=DE,BC=EF,AC=DF∠A=∠D,∠B=∠E,∠C=∠F全等三角形的性质:∵△ABC≌△DEFABCDEF∵△ABC≌△DEF
∴AB=DE,BC=EF,AC=DF.∴∠A= ∠D,∠B= ∠E,∠C= ∠F.ABCD∵△ABC≌△ABD∴AB=AB,BC=BD,AC=AD.∴∠BAC=∠BAD,∠ABC=∠ABD
∠C= ∠D.规律一:有公共边的,公共边是对应边ACODB∵△AOC≌△BOD∴AO=BO,AC=BD,OC=OD.∴∠A=∠B,∠C=∠D,
∠AOC= ∠BOD.规律二:有对顶角的,对顶角是对应角ABCDE∵△ABC≌△ADE∴AB=AD,AC=AE,BC=DE∴∠A=∠A,∠B=∠D,
∠ACB= ∠AED.规律三:有公共角的,公共角是对应角
ABCDE∵△ABC≌△DEC∴AB=DE,AC=DC,
BC=EC∴∠A=∠D,
∠B=∠E,
∠ACB= ∠DCE.规律四:一对最长的边是对应边
一对最短的边是对应边∵△ABC≌△FDE∴AB=FD,AC=FE,
BC=DE∴∠A=∠F,
∠B=∠D,
∠ACB= ∠FED.规律五:一对最大的角是对应角
一对最小的角是对应角已知△A0B≌△COD 指出图中两三角形的对应边和对应角已知△ABC≌△DCB 指出图中两三角形的对应边和对应角
找一找:请指出下列全等三角形的对应边和对应角1、 △ ABE ≌ △ ACF对应角是: ∠A和∠A、 ∠ABE和∠ACF、 ∠AEB和∠AFC;对应边是AB和AC、AE和AF、BE和CF。2、 △ BCE ≌ △ CBF对应角是: ∠BCE和 ∠CBF、 ∠BEC和∠CFB、 ∠CBE和 ∠BCF。对应边是:CB和BC、CE和BF、CF和BE。3、 △ BOF ≌ △ COE对应角是: ∠BOF和∠COE、 ∠BFO 和∠CEO、 ∠ FOB和∠EOC。对应边是:OF和OE、OB和OC、BF和CE。典型例题例1若ΔDEF≌ΔABC, ∠A=70°,∠B=50°,点A的对应点是点D,AB=DE,那么∠F的度数等于( )A.50° B.60° C.50° D.以上都不对分析: 由∠A=70°,∠B=50°知道:∠C=60°,所以ΔABC是不等边三角形,由点A的对应点是点D,AB=DE知道:∠F的对应角是∠C(60°)B典型例题例2如图,若ΔOAD≌ΔOBC, 且∠O=65°,∠C=20°,则∠OAD= .分析:由∠O=65°,∠C=20°知道, ∠OBC=95 °, 由ΔOAD≌ΔOBC知: ∠OAD=95 °。95 °典型例题例3:如图,若ΔABC≌ΔAEF, AB=AE,∠B=∠E,则下列结论:①AC=AF, ②∠FAB=∠EAB, ③EF=BC,④ ∠FAC=∠EAB,其中正确结论的个数是( ) A.1个 B.2个 C.3个 D.4个分析:由ΔABC≌ΔAEF和 ∠B=∠E知:AC=AF.所以①是正确的。①AC=AF,A典型例题例3:如图,若ΔABC≌ΔAEF, AB=AE,∠B=∠E,则下列结论:①AC=AF, ②∠FAB=∠EAB, ③EF=BC,④ ∠FAC=∠EAB,其中正确结论的个数是( ) A.1个 B.2个 C.3个 D.4个分析:由AB=AE和①AC=AF知: EF=BC ,所以③是正确的。③EF=BC典型例题例3:如图,若ΔABC≌ΔAEF, AB=AE,∠B=∠E,则下列结论:①AC=AF, ②∠FAB=∠EAB, ③EF=BC,④ ∠FAC=∠EAB,其中正确结论的个数是( ) A.1个 B.2个 C.3个 D.4个分析:由③EF=BC知: ∠BAC =∠EAF,得④ ∠FAC=∠EAB ,所以④是正确的。④ ∠FAC=∠EAB典型例题例3:如图,若ΔABC≌ΔAEF, AB=AE,∠B=∠E,则下列结论:①AC=AF, ②∠FAB=∠EAB, ③EF=BC,④ ∠FAC=∠EAB,其中正确结论的个数是( ) A.1个 B.2个 C.3个 D.4个分析:因为④∠FAC=∠EAB ,要使②∠FAB=∠EAB正确,必须有∠FAC= ∠FAB,而AF并不是角平分线,所以②不正确。C典型例题例4:如图,已知ΔABC≌ΔFED, BC=ED, 求证:AB∥EF证明: ∵ΔABC≌ΔFED, BC=ED ∴BC与ED是对应边
∴∠ =∠ , ( ) ∴ AB∥EF将上述证明过程补充完整.AF全等三角形的对应角相等典型例题例5:如图,已知ΔABD≌ΔAEC, ∠B和∠E,是对应角,AB与AE是对应边,试说明:BC=DE.分析: 因为ΔABD≌ΔAEC并且∠B和∠E是对应角,所以AD和AC是对应边,又因为AB与AE是对应边,所以BD和EC是对应边,即BD=EC,所以BD-CD=EC-CD,所以BC=DE.典型例题例6:如图,已知ΔAEF是ΔABC绕A点顺时针旋转55°得到的,求∠BAE,∠CAF和∠BME的度数.解:因为AE和AF分别是AB和AC旋转后的位置,所以∠BAE=∠CAF= 55°;又因为ΔAEF≌ΔABC,所以∠B=∠E, 因为∠ANB和∠ENM是对顶角,所以∠BME= ∠BAE= 55°;∠A+∠B=∠C+∠D典型例题例7:如图,已知ΔABE≌ΔACD,且∠1=∠2, ∠B=∠C,请指出其余的对应边和对应角.分析:由ΔABE≌ΔACD以及∠1=∠2, ∠B=∠C知:∠ BAE与∠CAD是对应角,根据“对应角的对边是对应边 ”可知:AD与AE,AE与AD,BE与CD分别是对应边.2. 叫做全等三角形。 1.能够重合的两个图形叫做 。全等形4.全等三角形的 和 相等对应边对应角对应顶点课 堂 小 结 能够重合的两个三角形3.“全等”用符号“ ”来表示,读作“ ”对应边对应角5.书写全等式时要求把对应字母放在对应
的位置上全等于≌ 其中:互相重合的顶点叫做___互相重合的边叫做____互相重合的角叫做___小结寻找对应元素的规律(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边,
最小的边是对应边;
(5)两个全等三角形最大的角是对应角,
最小的角是对应角;
思考一: 若你手上有一张长方形纸片,如何是长方形变成两个最大的全等三角形,而总面积又没有 变化?思考二:拓展与延伸 下图是一个等边三角形,你能把它分成两个全等三角形吗?你能把它分成三个全等三角形吗?四个呢? 再 见
