2024贵州中考数学二轮复习贵州中考题型研究 类型五 平行四边形问题课件 24张PPT
文档属性
| 名称 | 2024贵州中考数学二轮复习贵州中考题型研究 类型五 平行四边形问题课件 24张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-03 08:52:06 | ||
图片预览






文档简介
(共24张PPT)
类型五 平行四边形问题
函数微技能——分类讨论思想确定动点位置
一阶
例10 如图,已知抛物线交x轴于A、B两点(点A在点B左侧),与y轴交于点C,连接AC.
探究1:P是平面内一点,找出点P,使得以
A、B、C、P为顶点的四边形为平行四边形;
例10题图①
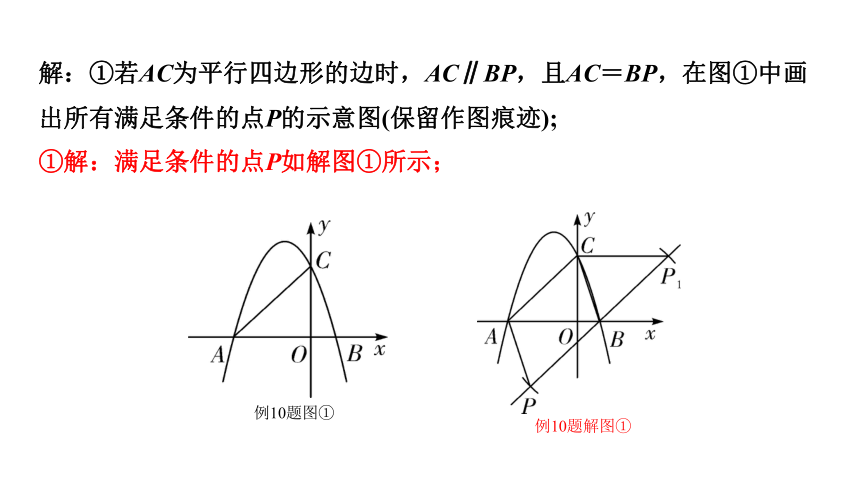
解:①若AC为平行四边形的边时,AC∥BP,且AC=BP,在图①中画出所有满足条件的点P的示意图(保留作图痕迹);
例10题图①
①解:满足条件的点P如解图①所示;
例10题解图①
【方法总结】二次函数中特殊四边形的存在性一般要分情况讨论:常以已知边为________或__________讨论;以探究1为例,若AC为边时,过点B作BP∥AC,点P可在x轴上方,也可在x轴下方;作图依据:____________________________________________________________;
若AC为对角线时,依据平行四边形对角线互相平分可得作法:____________________________________________________________.
边
对角线
一组对边平行且相等的四边形是平行四边形
取AC的中点D,连接BD并延长至点P,使得DP=DB.
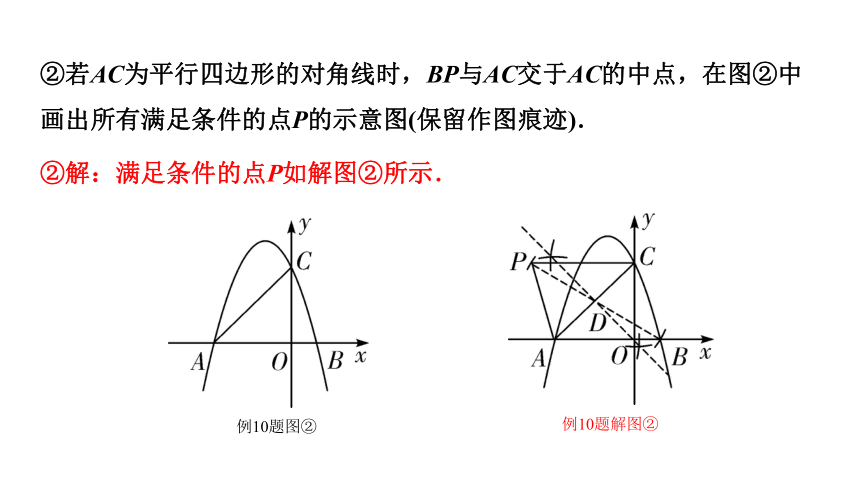
②若AC为平行四边形的对角线时,BP与AC交于AC的中点,在图②中画出所有满足条件的点P的示意图(保留作图痕迹).
例10题图②
②解:满足条件的点P如解图②所示.
例10题解图②
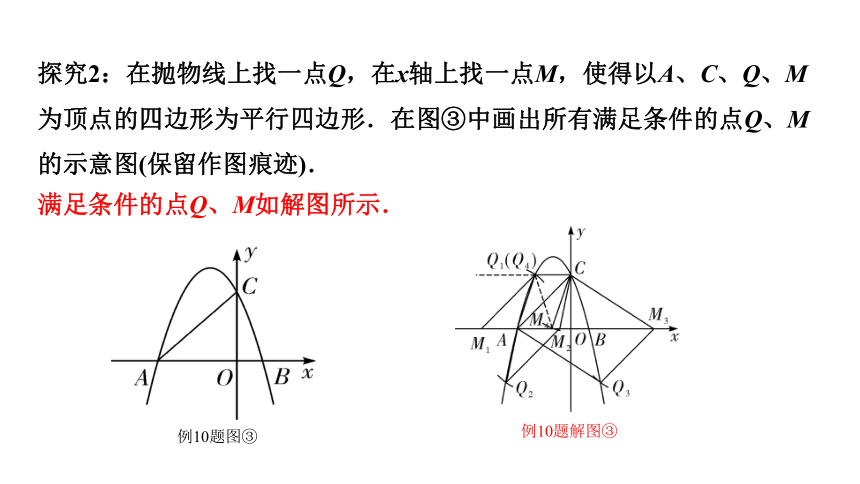
探究2:在抛物线上找一点Q,在x轴上找一点M,使得以A、C、Q、M为顶点的四边形为平行四边形.在图③中画出所有满足条件的点Q、M的示意图(保留作图痕迹).
例10题图③
满足条件的点Q、M如解图所示.
例10题解图③
设问突破
二阶
例11 如图,抛物线y=x2+6x+5与x轴交于A、B两点,与y轴交于点C,顶点为M,对称轴l与x轴的交点为D,与直线AC的交点为E.
一题多设问
(1)点G为x轴上一动点,在抛物线上是否存在点H,使得以A、C、G、H为顶点且AC为对角线的四边形是平行四边形?
若存在,求出点G的坐标;若不存在,请说明理由;
例11题图①
【思维教练】根据平行四边形对边平行且相等的性质即可求得点H坐标,进一步求得点G坐标;
(1)解:存在.
如解图①,过点C作x轴的平行线交抛物线于点H,连接AH,过点C作CG∥AH,与x轴的交点即为点G.
例11题图①
∵抛物线的解析式为y=x2+6x+5,
∴C(0,5),A(-5,0),
令y=5,即x2+6x+5=5,解得x1=0,x2=-6,
∴H(-6,5),∴CH=AG=6,∴G(1,0);
H
G
(2) 点P为直线AC上一动点,在直线AC下方的抛物线上是否存在点Q,使得以B、D、P、Q为顶点且BD为边的四边形是平行四边形?若存在,求出点Q的坐标;若不存在,请说明理由;
例11题图②
【思维教练】根据点P在直线AC上,设出点P、Q坐标,列等量关系式yP=yQ解方程即可;
(2)解:存在.
设直线AC的解析式为y=kx+d,
∴代入点A(-5,0),C(0,5),
解得 ,
∴直线AC的解析式为y=x+5.
∵BD=2,∴PQ=2.
设P(p,p+5),则Q(p+2,p2+10p+21).
由题意可知p+5=p2+10p+21,
解得p= 或p= ,
∴Q点的坐标为( , )或( , );
例11题图②
【思维教练】分AB为平行四边形的边和对角线两种情况进行讨论,分别求解即可;
(3)点S是抛物线对称轴上一点,点N是抛物线上一点,是否存在点N,使得以A、B、S、N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由;
例11题图③
(3)解:存在.
①当AB为平行四边形的边时,设N(n,n2+6n+5),则S(-3,n2+6n+5),
∵SN=AB,即|n+3|=4,解得n=1或n=-7.
∴点N的坐标为(1,12)或(-7,12);
②当AB为平行四边形对角线时,易得点N与点M重合,
∴点N的坐标为(-3,-4).
综上所述,符合题意的点N的坐标为(1,12)或(-7,12)
或(-3,-4);
例11题图③
【思维教练】根据点K、J分别为抛物线和直线AC上的点,设出点K坐标,即可表示出点J坐标,已知KJ∥ME,从而只需KJ=ME
即可得到平行四边形,再根据K、J点坐标及其相对位置,
列出等量关系式,即可求出点K坐标.
(4)设点K是抛物线上一点,过点K作KJ∥y轴,交直线AC于点J,是否存在点K,使得以M、E、K、J为顶点的四边形是平行四边形?若存在,求出点K的坐标;若不存在,请说明理由.
例11题图④
例11题解图②
(4)解:存在.
如解图②,设点K的坐标为(e,e2+6e+5).
∵KJ∥y轴,交直线AC于点J,直线AC的解析式为y=x+5,
∴点J的坐标为(e,e+5).
当x=-3时,y=(-3)+5=2,
∴E(-3,2), ∴ME=6.
∵ME∥y轴,KJ∥y轴, ∴KJ∥ME,
要使得以M,E,K,J为顶点的四边形为平行四边形,
只需KJ=ME=6.
①当点K在点J的下方时,
KJ=e+5-(e2+6e+5)=-e2-5e,
则-e2-5e=6,解得e1=-2,e2=-3,
则K1(-2,-3),K2(-3,-4)(与点M重合,舍去);
②当点K在点J的上方时,
KJ=(e2+6e+5)-(e+5)=e2+5e,
则e2+5e=6,解得e3=-6,e4=1,
则K3(-6,5),K4(1,12).
综上所述,点K的坐标为(-2,-3)或(-6,5)或(1,12).
例11题解图②
综合训练
三阶
6. (2023黔东南州26题14分)已知抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在点B的左边),与y轴交于点C(0,-3),顶点D的坐标为(1,-4).
(1)求抛物线的解析式;
第6题图
(1)解:∵抛物线交y轴于点(0,-3),
∴c=-3,
又∵顶点坐标为(1,-4),
∴ =1,即b=-2a, =-4,
即-3-a=-4,解得a=1,
∴b=-2,
∴抛物线解析式为y=x2-2x-3; (4分)
第6题图
(2)在y轴上找一点E,使得△EAC为等腰三角形,请直接写出点E的坐标;
第6题图
【解法提示】根据解析式y=x2-2x-3可得点A坐标为(-1,0),
∴AC= ,分三种情况:
①当以∠ACE为顶角时,可得纵坐标为 -3或- -3,
此时点E坐标为(0,-3)或(0,- -3);
②当以∠EAC为顶角时,可直接得到E的坐标为(0,3);
(2)(0, -3)或(0,- -3)
或(0,3)或(0,- );(8分)
第6题图
③当以∠AEC为顶角时,设点E纵坐标为m,
则m2+12=(m+3)2,解得m=- ,
∴点E的坐标为(0,- ),
综上所述,点E的坐标为(0,-3)或(0,- -3)或(0,3)或(0,- ).
(3)点P是x轴上的动点,点Q是抛物线上的动点,是否存在点P、Q,使得以点P、Q、B、D为顶点,BD为一边的四边形是平行四边形?若存在,请求出点P、Q坐标;若不存在,请说明理由.
(3)解:存在.令x2-2x-3=0,解得x1=-1,x2=3,
∴点A坐标为(-1,0),点B坐标为(3,0),以BD为边
作平行四边形,则另一边PQ可利用平移得到,且根据
平行四边形的中心对称性,点Q和点D距离x轴的距离
相等,都为4.
当x2-2x-3=4时,x1=1+2 ,x2=1-2 ,
第6题图
即点Q的坐标为(1+2 ,4),点P的坐标(-1+2 ,0)
或点Q的坐标为(1-2 ,4),点P的坐标(-1-2 ,0).
当x2-2x-3=-4时,x1=x2=1,与点D重合,不能构成平行四边形.
综上所述,点Q的坐标为(1+2 ,4),点P的坐标(-1+2 ,0)
或点Q的坐标为(1-2 ,4),点P的坐标(-1-2 ,0).(14分)
第6题图
【一题多解】存在.
∵D(1,-4),
∴将线段BD向上平移4个单位,再向右(或向左)平移适当的距离,使点B的对应点落在抛物线上,这点便是点Q,当然此时点D的对应点便是点P,
∴点Q的纵坐标为4,
设Q(t,4),代入抛物线y=x2-2x-3得:
t2-2t-3=4,即t2-2t-7=0,
解得t1=1+2 ,t2=1-2 ,
此时,Q1(1+2 ,4)或Q2(1-2 ,4),
第6题图
如解图,分别过点D、Q1、Q2作x轴的垂线,垂足分别为点F、G1、G2.
∵抛物线y=x2-2x-3与x轴的右交点B的坐标为(3,0),D(1,-4),
∴FB=PG=3-1=2,
∴点P1的横坐标为(1+2 )-2=-1+2 ,
点P2的横坐标为(1-2 )-2=-1-2 .
综上,点P、Q的坐标为
P(-1+2 ,0),Q(1+2 ,4),
或P(-1-2 ,0),Q(1-2 ,4). (14分)
第6题解图
类型五 平行四边形问题
函数微技能——分类讨论思想确定动点位置
一阶
例10 如图,已知抛物线交x轴于A、B两点(点A在点B左侧),与y轴交于点C,连接AC.
探究1:P是平面内一点,找出点P,使得以
A、B、C、P为顶点的四边形为平行四边形;
例10题图①
解:①若AC为平行四边形的边时,AC∥BP,且AC=BP,在图①中画出所有满足条件的点P的示意图(保留作图痕迹);
例10题图①
①解:满足条件的点P如解图①所示;
例10题解图①
【方法总结】二次函数中特殊四边形的存在性一般要分情况讨论:常以已知边为________或__________讨论;以探究1为例,若AC为边时,过点B作BP∥AC,点P可在x轴上方,也可在x轴下方;作图依据:____________________________________________________________;
若AC为对角线时,依据平行四边形对角线互相平分可得作法:____________________________________________________________.
边
对角线
一组对边平行且相等的四边形是平行四边形
取AC的中点D,连接BD并延长至点P,使得DP=DB.
②若AC为平行四边形的对角线时,BP与AC交于AC的中点,在图②中画出所有满足条件的点P的示意图(保留作图痕迹).
例10题图②
②解:满足条件的点P如解图②所示.
例10题解图②
探究2:在抛物线上找一点Q,在x轴上找一点M,使得以A、C、Q、M为顶点的四边形为平行四边形.在图③中画出所有满足条件的点Q、M的示意图(保留作图痕迹).
例10题图③
满足条件的点Q、M如解图所示.
例10题解图③
设问突破
二阶
例11 如图,抛物线y=x2+6x+5与x轴交于A、B两点,与y轴交于点C,顶点为M,对称轴l与x轴的交点为D,与直线AC的交点为E.
一题多设问
(1)点G为x轴上一动点,在抛物线上是否存在点H,使得以A、C、G、H为顶点且AC为对角线的四边形是平行四边形?
若存在,求出点G的坐标;若不存在,请说明理由;
例11题图①
【思维教练】根据平行四边形对边平行且相等的性质即可求得点H坐标,进一步求得点G坐标;
(1)解:存在.
如解图①,过点C作x轴的平行线交抛物线于点H,连接AH,过点C作CG∥AH,与x轴的交点即为点G.
例11题图①
∵抛物线的解析式为y=x2+6x+5,
∴C(0,5),A(-5,0),
令y=5,即x2+6x+5=5,解得x1=0,x2=-6,
∴H(-6,5),∴CH=AG=6,∴G(1,0);
H
G
(2) 点P为直线AC上一动点,在直线AC下方的抛物线上是否存在点Q,使得以B、D、P、Q为顶点且BD为边的四边形是平行四边形?若存在,求出点Q的坐标;若不存在,请说明理由;
例11题图②
【思维教练】根据点P在直线AC上,设出点P、Q坐标,列等量关系式yP=yQ解方程即可;
(2)解:存在.
设直线AC的解析式为y=kx+d,
∴代入点A(-5,0),C(0,5),
解得 ,
∴直线AC的解析式为y=x+5.
∵BD=2,∴PQ=2.
设P(p,p+5),则Q(p+2,p2+10p+21).
由题意可知p+5=p2+10p+21,
解得p= 或p= ,
∴Q点的坐标为( , )或( , );
例11题图②
【思维教练】分AB为平行四边形的边和对角线两种情况进行讨论,分别求解即可;
(3)点S是抛物线对称轴上一点,点N是抛物线上一点,是否存在点N,使得以A、B、S、N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由;
例11题图③
(3)解:存在.
①当AB为平行四边形的边时,设N(n,n2+6n+5),则S(-3,n2+6n+5),
∵SN=AB,即|n+3|=4,解得n=1或n=-7.
∴点N的坐标为(1,12)或(-7,12);
②当AB为平行四边形对角线时,易得点N与点M重合,
∴点N的坐标为(-3,-4).
综上所述,符合题意的点N的坐标为(1,12)或(-7,12)
或(-3,-4);
例11题图③
【思维教练】根据点K、J分别为抛物线和直线AC上的点,设出点K坐标,即可表示出点J坐标,已知KJ∥ME,从而只需KJ=ME
即可得到平行四边形,再根据K、J点坐标及其相对位置,
列出等量关系式,即可求出点K坐标.
(4)设点K是抛物线上一点,过点K作KJ∥y轴,交直线AC于点J,是否存在点K,使得以M、E、K、J为顶点的四边形是平行四边形?若存在,求出点K的坐标;若不存在,请说明理由.
例11题图④
例11题解图②
(4)解:存在.
如解图②,设点K的坐标为(e,e2+6e+5).
∵KJ∥y轴,交直线AC于点J,直线AC的解析式为y=x+5,
∴点J的坐标为(e,e+5).
当x=-3时,y=(-3)+5=2,
∴E(-3,2), ∴ME=6.
∵ME∥y轴,KJ∥y轴, ∴KJ∥ME,
要使得以M,E,K,J为顶点的四边形为平行四边形,
只需KJ=ME=6.
①当点K在点J的下方时,
KJ=e+5-(e2+6e+5)=-e2-5e,
则-e2-5e=6,解得e1=-2,e2=-3,
则K1(-2,-3),K2(-3,-4)(与点M重合,舍去);
②当点K在点J的上方时,
KJ=(e2+6e+5)-(e+5)=e2+5e,
则e2+5e=6,解得e3=-6,e4=1,
则K3(-6,5),K4(1,12).
综上所述,点K的坐标为(-2,-3)或(-6,5)或(1,12).
例11题解图②
综合训练
三阶
6. (2023黔东南州26题14分)已知抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在点B的左边),与y轴交于点C(0,-3),顶点D的坐标为(1,-4).
(1)求抛物线的解析式;
第6题图
(1)解:∵抛物线交y轴于点(0,-3),
∴c=-3,
又∵顶点坐标为(1,-4),
∴ =1,即b=-2a, =-4,
即-3-a=-4,解得a=1,
∴b=-2,
∴抛物线解析式为y=x2-2x-3; (4分)
第6题图
(2)在y轴上找一点E,使得△EAC为等腰三角形,请直接写出点E的坐标;
第6题图
【解法提示】根据解析式y=x2-2x-3可得点A坐标为(-1,0),
∴AC= ,分三种情况:
①当以∠ACE为顶角时,可得纵坐标为 -3或- -3,
此时点E坐标为(0,-3)或(0,- -3);
②当以∠EAC为顶角时,可直接得到E的坐标为(0,3);
(2)(0, -3)或(0,- -3)
或(0,3)或(0,- );(8分)
第6题图
③当以∠AEC为顶角时,设点E纵坐标为m,
则m2+12=(m+3)2,解得m=- ,
∴点E的坐标为(0,- ),
综上所述,点E的坐标为(0,-3)或(0,- -3)或(0,3)或(0,- ).
(3)点P是x轴上的动点,点Q是抛物线上的动点,是否存在点P、Q,使得以点P、Q、B、D为顶点,BD为一边的四边形是平行四边形?若存在,请求出点P、Q坐标;若不存在,请说明理由.
(3)解:存在.令x2-2x-3=0,解得x1=-1,x2=3,
∴点A坐标为(-1,0),点B坐标为(3,0),以BD为边
作平行四边形,则另一边PQ可利用平移得到,且根据
平行四边形的中心对称性,点Q和点D距离x轴的距离
相等,都为4.
当x2-2x-3=4时,x1=1+2 ,x2=1-2 ,
第6题图
即点Q的坐标为(1+2 ,4),点P的坐标(-1+2 ,0)
或点Q的坐标为(1-2 ,4),点P的坐标(-1-2 ,0).
当x2-2x-3=-4时,x1=x2=1,与点D重合,不能构成平行四边形.
综上所述,点Q的坐标为(1+2 ,4),点P的坐标(-1+2 ,0)
或点Q的坐标为(1-2 ,4),点P的坐标(-1-2 ,0).(14分)
第6题图
【一题多解】存在.
∵D(1,-4),
∴将线段BD向上平移4个单位,再向右(或向左)平移适当的距离,使点B的对应点落在抛物线上,这点便是点Q,当然此时点D的对应点便是点P,
∴点Q的纵坐标为4,
设Q(t,4),代入抛物线y=x2-2x-3得:
t2-2t-3=4,即t2-2t-7=0,
解得t1=1+2 ,t2=1-2 ,
此时,Q1(1+2 ,4)或Q2(1-2 ,4),
第6题图
如解图,分别过点D、Q1、Q2作x轴的垂线,垂足分别为点F、G1、G2.
∵抛物线y=x2-2x-3与x轴的右交点B的坐标为(3,0),D(1,-4),
∴FB=PG=3-1=2,
∴点P1的横坐标为(1+2 )-2=-1+2 ,
点P2的横坐标为(1-2 )-2=-1-2 .
综上,点P、Q的坐标为
P(-1+2 ,0),Q(1+2 ,4),
或P(-1-2 ,0),Q(1-2 ,4). (14分)
第6题解图
同课章节目录
