热点35 带电粒子在空间电场和磁场中的运动 --高考物理50热点冲刺精练(名师解析)
文档属性
| 名称 | 热点35 带电粒子在空间电场和磁场中的运动 --高考物理50热点冲刺精练(名师解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-04-03 11:17:46 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024高考物理50热点冲刺训练
热点35 带电粒子在空间电场和磁场中的运动
1.(16分)(2024安徽”江南十校”3月联考)如图甲所示,三维直角坐标系Oyz中,在的区域中,存在沿z轴负方向的匀强磁场;在的区域中,存在沿y轴正方向的匀强磁场,两区域的磁感应强度的大小相同。如图乙所示,原点O处有一粒子源,可在xOy平面内向Ⅰ、Ⅱ象限各个方向连续发射大量质量为m,电荷量为的粒子,速度大小在之间。在x轴上垂直于xOy平面放置着一块足够长的薄板,粒子在薄板上轰击的区域的长度为。不考虑粒子间的相互作用,不计粒子的重力。
(1)匀强磁场磁感应强度B的大小;
(2)在薄板上处开一个小孔,粒子源发射的部分粒子会穿过小孔进入的区域。在处垂直于y轴放置一圆形荧光屏,屏幕的圆心在y轴上。求打在荧光屏上的粒子,在磁场中运动的最短时间与最长时间的比值(提示:在磁场中运动最短时间与最长时间的粒子,从小孔穿过时的速度大小均为);
(3)在(2)问中,为了让所有穿过长薄板的粒子均能打到荧光屏上,求荧光屏的最小半径R。
【参考答案】(1),(2)(3)
【名师解析】(1)速度为的粒子沿y轴正向发射,打在薄板的最远处,其在磁场中运动的半径为,由牛顿第二定律
由几何关系
联立,解得
(2)如图所示
速度为v的粒子与x轴成α角射出,恰好穿过小孔,在磁场中运动时,由牛顿第二定律
由几何关系
粒子沿y轴方向的分速度
联立,解得
结果表明,能穿过小孔的粒子具有相同的沿y轴方向的分速度
粒子穿过小孔进入的区域中做螺旋运动,其圆周运动周期
y轴方向匀速,到达屏幕时间
i.如图a所示,当粒子以速度穿过小孔,,此时在在的区域中运动时间最短,即总时间最短
ⅱ.如图b所示,当粒子以速度穿过小孔,,此时在在的区域中运动时间最长,即总时间最长
故
(3)如图所示
粒子旋转一圈半到达屏幕,当粒子以速度为从O点射入,可以到达离荧光屏圆心的最远处。粒子进入的区域时,沿x轴方向的初速度为,有,
对应半径为
联立,解得
荧光屏的最小半径
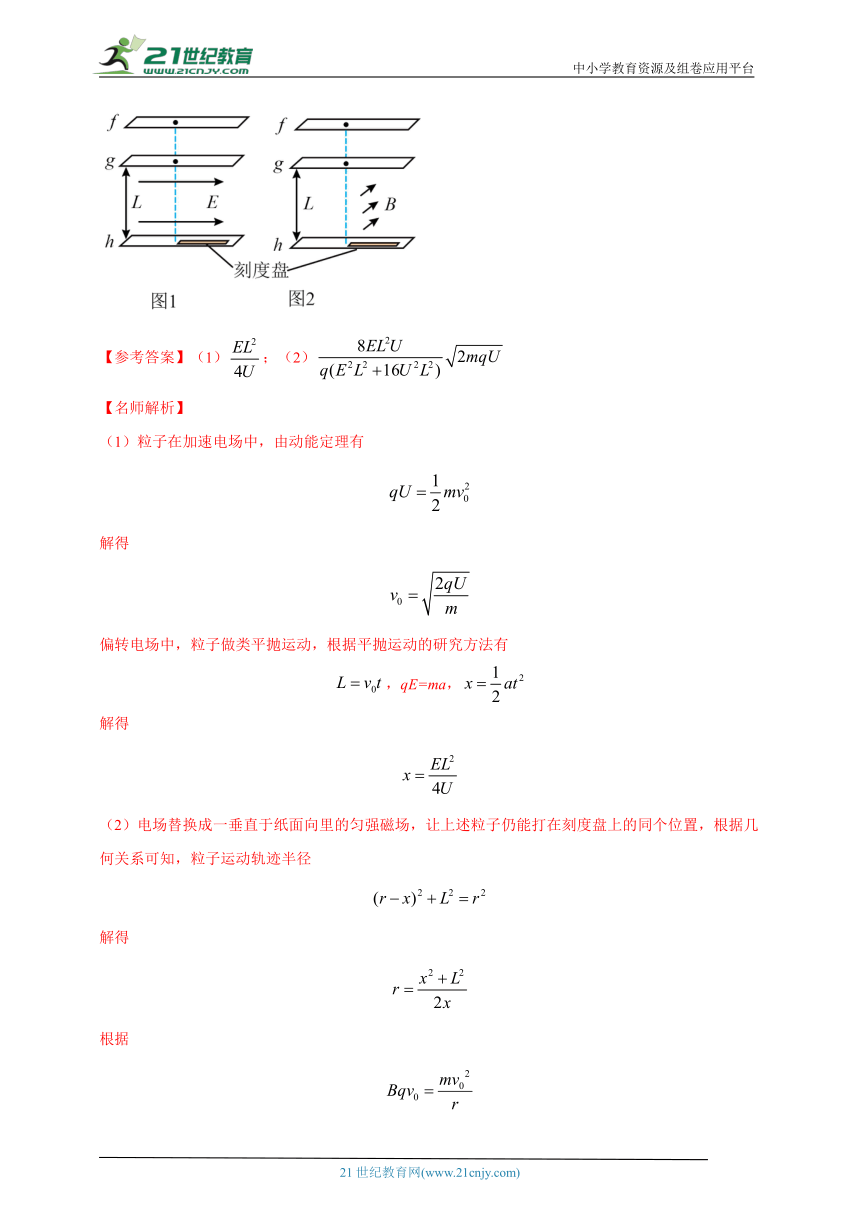
2. (2024广东潮州质检)如图1所示,竖直面内水平放置两块平行的带电异体板,,两板在同一竖直线上开着两个小孔。一质量为、电荷量为的带正电粒子从板的小孔无初速飞入,经过,板的电场加速后,经第二个小孔进入板下方空间的电场,最后落在水平荧光屏上刻度盘的某个位置,该位置与导体板,两小孔所在竖直线的距离为(为未知量)。已知,两板之间的电势差大小为,板到板的距离为,板下方的电场方向水平向右,场强大小为不考虑带电粒子所受重力对上述问题的影响,求:
(1)的表达式;
(2)若将、两板之间的电场替换成一垂直于纸面向里的匀强磁场,如图2所示,要让上述粒子仍能打在刻度盘上的同个位置,求替换后的磁场的磁感应强度的大小。
【参考答案】(1);(2)
【名师解析】
(1)粒子在加速电场中,由动能定理有
解得
偏转电场中,粒子做类平抛运动,根据平抛运动的研究方法有
,qE=ma,
解得
(2)电场替换成一垂直于纸面向里的匀强磁场,让上述粒子仍能打在刻度盘上的同个位置,根据几何关系可知,粒子运动轨迹半径
解得
根据
解得
3. (2024山东济南期末)如图所示,在空间直角坐标系内有一边长为L的正方体区域,面在平面内,坐标原点O位于面的中心,整个空间存在沿y轴正方向的匀强电场,在的空间区域Ⅰ内和的空间区域Ⅱ内均存在沿y轴正方向的匀强磁场(区域Ⅰ内和区域Ⅱ内磁感应强度大小可独立调节)。一可控制发射粒子数量和方向的粒子源位于坐标原点,发射粒子的质量均为m,电荷量均为,初速度大小均为,不计粒子重力和粒子间的相互作用。
(1)将整个空间内的磁感应强度的大小均调节为零,控制粒子源沿x轴正方向发射一个带电粒子,该粒子恰好经过面的中心,求所加匀强电场电场强度的大小E;
(2)将区域Ⅰ、Ⅱ内的磁感应强度的大小均调节为,控制粒子源在平面内沿各个方向均匀发射带电粒子,求从面射出的粒子中,射出位置y坐标的最小值;
(3)将区域Ⅰ内的磁感应强度的大小调节为,将区域Ⅱ内的磁感应强度的大小调节为控制粒子源沿x轴正方向发射一个带电粒子,粒子第6次(粒子源发射粒子时为第0次)穿过平面时,恰好从的中点处离开正方体区域,求磁感应强度的大小。
【参考答案】(1);(2);
(3),
【名师解析】
(1)离子甲在电场中做类似平抛运动
解得
(2)粒子的运动可分解为面内的匀速圆周运动和y轴方向的匀加速直线运动,要使出射时y坐标最小,需使运动时间最短,时间最短时在面内的做匀速圆周运动的圆心角最小,弦长最短,有几何关系知最短弦长为。根据洛伦兹力提供向心力
解得
由几何关系得圆心角
解得:
解得:
(3)由几何关系可得
解得:
,
4. (2024江苏南京27中期末) 如图所示,在空间坐标系中,区域Ⅰ是边长为的正方体空间,该空间内存在沿轴正方向的匀强磁场,磁感应强度大小为(大小未知),区域Ⅱ也是边长为的正方体空间,该空间内存在沿轴正方向的匀强磁场,磁感应强度大小为(大小未知),区域Ⅱ的上表面是一粒子收集板。一质量为、电荷量为的带电粒子从坐标原点沿平面以初速度进入区域Ⅰ,然后从区域Ⅰ右边界上的点沿轴正方向进入区域Ⅱ。已知点的坐标为,粒子重力不计。
(1)求磁感应强度的大小;
(2)为使粒子能够在区域II中直接打到粒子收集板上,求磁感应强度的大小范围。
【参考答案】(1);(2)
【名师解析】
(1)带电粒子在区域Ⅰ中做匀速圆周运动,由洛伦兹力提供向心力得
由几何关系可知
可得
联立可得,磁感应强度的大小为
(2)为了保证粒子能够直接打到粒子收集板上,最小半径为
最大半径为
由洛伦兹力提供向心力得
联立可得,磁感应强度的大小范围为
5. (2024山东济南期末)如图甲所示,一个棱长为的立方体空间中存在着磁感应强度大小为,沿轴负方向的匀强磁场,质量为、电量为的带正电的粒子从左侧面的中心沿轴正方向射入立方体空间,粒子重力忽略不计。
(1)若粒子的速度大小任意取值,求粒子在磁场中运动的最长时间;
(2)若粒子从面射出,求粒子速度大小的取值范围;
(3)如图乙所示,将磁场撤掉,在立方体空间中加上沿轴正方向的匀强电场,粒子射出时的速度方向偏转了。如图丙所示,保持粒子的入射速度不变,再将立体空间分成左右相等的两个区域,左侧区域保持电场不变,右侧区域加上沿轴负方向的匀强磁场,磁感应强度大小为。粒子先后穿过电场和磁场区域,垂直面射出,求电场强度。
【参考答案】(1);(2);(3)
【名师解析】
(1)由分析可知,粒子从左侧面飞出时时间最长。由向心力公式得
运动周期为
粒子在磁场中运动的圆心角为
解得
(2)若从棱射出时,沿y轴负方向看去,粒子的运动轨迹如图
由几何知识得:
若从棱射出时,沿y轴负方向看去,粒子的运动轨迹如图
由几何知识得
解得
(3)设粒子离开电场时沿轴的速度为,粒子射出时的速度偏转了45°,所以
,,
所以
可知粒子恰好从棱射出。
,
当右侧区域换成磁场时,由于水平位移变为原来的一半,所以电场中的运动时间也变为原来的一半,偏转位移
,,
粒子进入磁场时速度与轴的夹角为
设粒子在磁场中的运动半径为
,
联立解得
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2024高考物理50热点冲刺训练
热点35 带电粒子在空间电场和磁场中的运动
1.(16分)(2024安徽”江南十校”3月联考)如图甲所示,三维直角坐标系Oyz中,在的区域中,存在沿z轴负方向的匀强磁场;在的区域中,存在沿y轴正方向的匀强磁场,两区域的磁感应强度的大小相同。如图乙所示,原点O处有一粒子源,可在xOy平面内向Ⅰ、Ⅱ象限各个方向连续发射大量质量为m,电荷量为的粒子,速度大小在之间。在x轴上垂直于xOy平面放置着一块足够长的薄板,粒子在薄板上轰击的区域的长度为。不考虑粒子间的相互作用,不计粒子的重力。
(1)匀强磁场磁感应强度B的大小;
(2)在薄板上处开一个小孔,粒子源发射的部分粒子会穿过小孔进入的区域。在处垂直于y轴放置一圆形荧光屏,屏幕的圆心在y轴上。求打在荧光屏上的粒子,在磁场中运动的最短时间与最长时间的比值(提示:在磁场中运动最短时间与最长时间的粒子,从小孔穿过时的速度大小均为);
(3)在(2)问中,为了让所有穿过长薄板的粒子均能打到荧光屏上,求荧光屏的最小半径R。
【参考答案】(1),(2)(3)
【名师解析】(1)速度为的粒子沿y轴正向发射,打在薄板的最远处,其在磁场中运动的半径为,由牛顿第二定律
由几何关系
联立,解得
(2)如图所示
速度为v的粒子与x轴成α角射出,恰好穿过小孔,在磁场中运动时,由牛顿第二定律
由几何关系
粒子沿y轴方向的分速度
联立,解得
结果表明,能穿过小孔的粒子具有相同的沿y轴方向的分速度
粒子穿过小孔进入的区域中做螺旋运动,其圆周运动周期
y轴方向匀速,到达屏幕时间
i.如图a所示,当粒子以速度穿过小孔,,此时在在的区域中运动时间最短,即总时间最短
ⅱ.如图b所示,当粒子以速度穿过小孔,,此时在在的区域中运动时间最长,即总时间最长
故
(3)如图所示
粒子旋转一圈半到达屏幕,当粒子以速度为从O点射入,可以到达离荧光屏圆心的最远处。粒子进入的区域时,沿x轴方向的初速度为,有,
对应半径为
联立,解得
荧光屏的最小半径
2. (2024广东潮州质检)如图1所示,竖直面内水平放置两块平行的带电异体板,,两板在同一竖直线上开着两个小孔。一质量为、电荷量为的带正电粒子从板的小孔无初速飞入,经过,板的电场加速后,经第二个小孔进入板下方空间的电场,最后落在水平荧光屏上刻度盘的某个位置,该位置与导体板,两小孔所在竖直线的距离为(为未知量)。已知,两板之间的电势差大小为,板到板的距离为,板下方的电场方向水平向右,场强大小为不考虑带电粒子所受重力对上述问题的影响,求:
(1)的表达式;
(2)若将、两板之间的电场替换成一垂直于纸面向里的匀强磁场,如图2所示,要让上述粒子仍能打在刻度盘上的同个位置,求替换后的磁场的磁感应强度的大小。
【参考答案】(1);(2)
【名师解析】
(1)粒子在加速电场中,由动能定理有
解得
偏转电场中,粒子做类平抛运动,根据平抛运动的研究方法有
,qE=ma,
解得
(2)电场替换成一垂直于纸面向里的匀强磁场,让上述粒子仍能打在刻度盘上的同个位置,根据几何关系可知,粒子运动轨迹半径
解得
根据
解得
3. (2024山东济南期末)如图所示,在空间直角坐标系内有一边长为L的正方体区域,面在平面内,坐标原点O位于面的中心,整个空间存在沿y轴正方向的匀强电场,在的空间区域Ⅰ内和的空间区域Ⅱ内均存在沿y轴正方向的匀强磁场(区域Ⅰ内和区域Ⅱ内磁感应强度大小可独立调节)。一可控制发射粒子数量和方向的粒子源位于坐标原点,发射粒子的质量均为m,电荷量均为,初速度大小均为,不计粒子重力和粒子间的相互作用。
(1)将整个空间内的磁感应强度的大小均调节为零,控制粒子源沿x轴正方向发射一个带电粒子,该粒子恰好经过面的中心,求所加匀强电场电场强度的大小E;
(2)将区域Ⅰ、Ⅱ内的磁感应强度的大小均调节为,控制粒子源在平面内沿各个方向均匀发射带电粒子,求从面射出的粒子中,射出位置y坐标的最小值;
(3)将区域Ⅰ内的磁感应强度的大小调节为,将区域Ⅱ内的磁感应强度的大小调节为控制粒子源沿x轴正方向发射一个带电粒子,粒子第6次(粒子源发射粒子时为第0次)穿过平面时,恰好从的中点处离开正方体区域,求磁感应强度的大小。
【参考答案】(1);(2);
(3),
【名师解析】
(1)离子甲在电场中做类似平抛运动
解得
(2)粒子的运动可分解为面内的匀速圆周运动和y轴方向的匀加速直线运动,要使出射时y坐标最小,需使运动时间最短,时间最短时在面内的做匀速圆周运动的圆心角最小,弦长最短,有几何关系知最短弦长为。根据洛伦兹力提供向心力
解得
由几何关系得圆心角
解得:
解得:
(3)由几何关系可得
解得:
,
4. (2024江苏南京27中期末) 如图所示,在空间坐标系中,区域Ⅰ是边长为的正方体空间,该空间内存在沿轴正方向的匀强磁场,磁感应强度大小为(大小未知),区域Ⅱ也是边长为的正方体空间,该空间内存在沿轴正方向的匀强磁场,磁感应强度大小为(大小未知),区域Ⅱ的上表面是一粒子收集板。一质量为、电荷量为的带电粒子从坐标原点沿平面以初速度进入区域Ⅰ,然后从区域Ⅰ右边界上的点沿轴正方向进入区域Ⅱ。已知点的坐标为,粒子重力不计。
(1)求磁感应强度的大小;
(2)为使粒子能够在区域II中直接打到粒子收集板上,求磁感应强度的大小范围。
【参考答案】(1);(2)
【名师解析】
(1)带电粒子在区域Ⅰ中做匀速圆周运动,由洛伦兹力提供向心力得
由几何关系可知
可得
联立可得,磁感应强度的大小为
(2)为了保证粒子能够直接打到粒子收集板上,最小半径为
最大半径为
由洛伦兹力提供向心力得
联立可得,磁感应强度的大小范围为
5. (2024山东济南期末)如图甲所示,一个棱长为的立方体空间中存在着磁感应强度大小为,沿轴负方向的匀强磁场,质量为、电量为的带正电的粒子从左侧面的中心沿轴正方向射入立方体空间,粒子重力忽略不计。
(1)若粒子的速度大小任意取值,求粒子在磁场中运动的最长时间;
(2)若粒子从面射出,求粒子速度大小的取值范围;
(3)如图乙所示,将磁场撤掉,在立方体空间中加上沿轴正方向的匀强电场,粒子射出时的速度方向偏转了。如图丙所示,保持粒子的入射速度不变,再将立体空间分成左右相等的两个区域,左侧区域保持电场不变,右侧区域加上沿轴负方向的匀强磁场,磁感应强度大小为。粒子先后穿过电场和磁场区域,垂直面射出,求电场强度。
【参考答案】(1);(2);(3)
【名师解析】
(1)由分析可知,粒子从左侧面飞出时时间最长。由向心力公式得
运动周期为
粒子在磁场中运动的圆心角为
解得
(2)若从棱射出时,沿y轴负方向看去,粒子的运动轨迹如图
由几何知识得:
若从棱射出时,沿y轴负方向看去,粒子的运动轨迹如图
由几何知识得
解得
(3)设粒子离开电场时沿轴的速度为,粒子射出时的速度偏转了45°,所以
,,
所以
可知粒子恰好从棱射出。
,
当右侧区域换成磁场时,由于水平位移变为原来的一半,所以电场中的运动时间也变为原来的一半,偏转位移
,,
粒子进入磁场时速度与轴的夹角为
设粒子在磁场中的运动半径为
,
联立解得
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
