热点48 热学+液柱与变质量 --高考物理50热点冲刺精练(名师解析)
文档属性
| 名称 | 热点48 热学+液柱与变质量 --高考物理50热点冲刺精练(名师解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-04-03 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024高考物理50热点冲刺训练
热点48 热学+液柱与变质量
1. (2024山东德州期末) 如图所示,10℃的氧气和20℃的氢气体积相同,汞柱在连通两容器的细管中央,下面的叙述中,正确的是( )
A. 当氧气和氢气的温度都升高10℃时,汞柱不移动
B. 当氧气和氢气的温度都升高10℃时,汞柱将向左移
C. 当氧气温度升高10℃,氢气温度升高20℃时,汞柱向左移
D. 当氧气温度升高10℃,氢气温度升高20℃时,汞柱不会移动
【参考答案】C
【名师解析】
假设两部分气体的体积不变,设气体初始状态的参量为p1、T1,末状态参量为p2、T2,变化温度为ΔT、变化压强为Δp,由查理定律有
可得
开始时两部分气体的压强p相同,若变化过程中ΔT相同,因为 T氧由
得 Δp氧>Δp氢
所以汞柱向右移动,故AB错误。
开始时两部分气体的压强p相同,T氧=283K,T氢=293K,若ΔT氧=10K,ΔT氢=20K,由
得 Δp氧<Δp氢
所以汞柱向左移,故C正确,D错误。
2. (2024河北保定部分学校期末) 桶装纯净水及压水装置原理如图所示。柱形水桶直径为24cm,高为35cm;柱形压水气囊直径为6cm,高为8cm;水桶颈部的长度为10cm。当人用力向下压气囊时,气囊中的空气被压入桶内,桶内气体的压强增大,水通过细出水管流出。已知水桶所在处大气压强相当于10m高水柱产生的压强,当桶内的水还剩5cm高时,桶内气体的压强等于大气压强,忽略水桶颈部的体积。至少需要把气囊完全压下几次,才能有水从细出水管流出?(不考虑温度的变化)( )
A. 1次 B. 2次 C. 3次 D. 4次
【参考答案】C
【名师解析】
设大气压强为p0,水桶内气体体积为V0,气囊体积为V1,至少需要把气囊完全压下n次,桶内气体压强增加为p1,才能有水从细出水管流出,水桶内气体体积不变,温度不变,根据玻意耳定律可得
其中
联立解得
n=2.4
即至少需要把气囊完全压3次,故C正确,ABD错误。
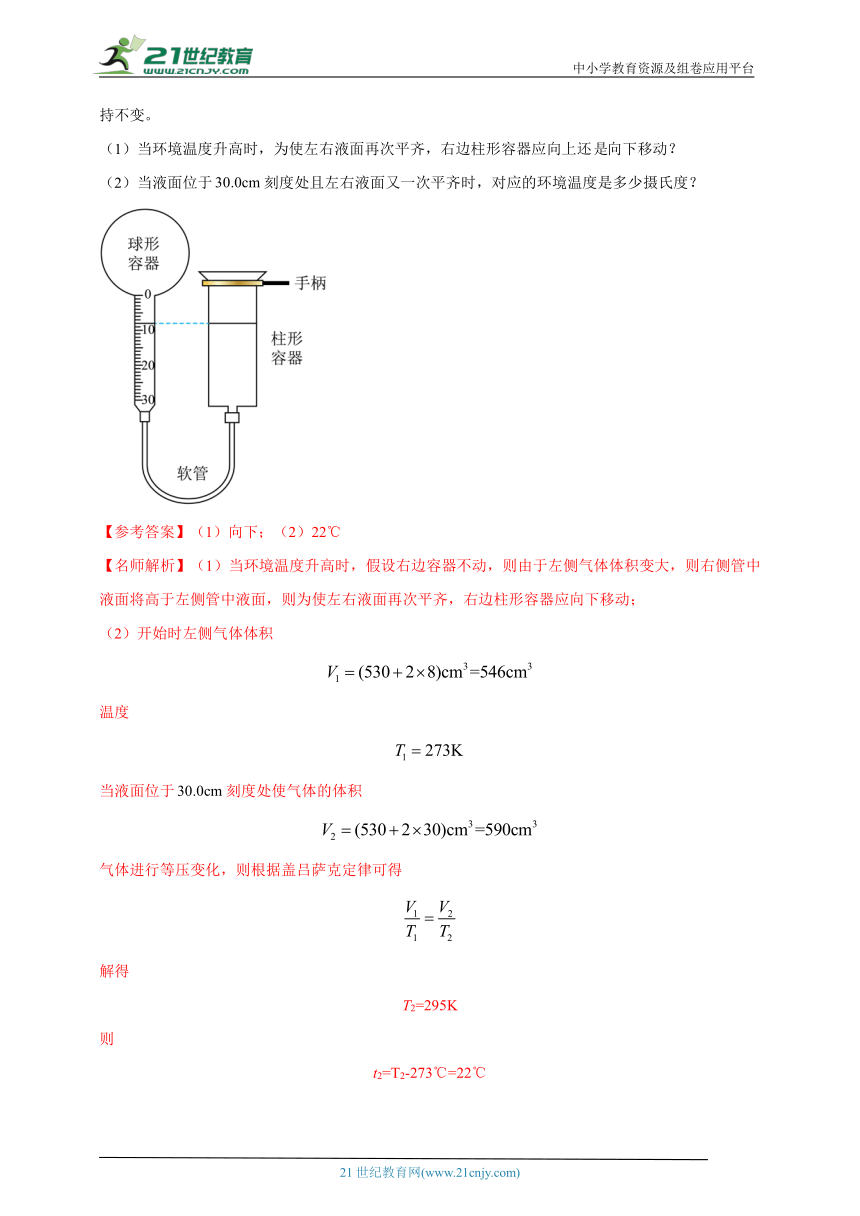
3. (2024贵州高考适应性考试)下图是一个简易温度计示意图,左边由固定的玻璃球形容器和内径均匀且标有刻度的竖直玻璃管组成,右边是上端开口的柱形玻璃容器,左右两边通过软管连接,用水银将一定质量的空气封闭在左边容器中。已知球形容器的容积为,左边玻璃管内部的横截面积为。当环境温度为且左右液面平齐时,左管液面正好位于刻度处。设大气压强保持不变。
(1)当环境温度升高时,为使左右液面再次平齐,右边柱形容器应向上还向下移动?
(2)当液面位于刻度处且左右液面又一次平齐时,对应的环境温度是多少摄氏度?
【参考答案】(1)向下;(2)22℃
【名师解析】(1)当环境温度升高时,假设右边容器不动,则由于左侧气体体积变大,则右侧管中液面将高于左侧管中液面,则为使左右液面再次平齐,右边柱形容器应向下移动;
(2)开始时左侧气体体积
温度
当液面位于刻度处使气体的体积
气体进行等压变化,则根据盖吕萨克定律可得
解得
T2=295K
则
t2=T2-273℃=22℃
4.(12分)(2024年辽宁顶级名校质检)如图所示,小明用仪器测一质量为的生肖摆件的密度。已知密闭容器的容积为,抽气筒的容积为,把生肖摆件放入密闭容器,抽气筒与密闭容器通过单向阀门相连,活塞从抽气筒的左端向右移动到右端的过程中,阀门开启,密闭容器内的气体进入抽气筒,活塞从右端向左移动到左端过程中,阀门关闭,抽气筒内活塞左侧的气体被排出,完成一次抽气过程。开始时密闭容器内空气压强为,抽气一次后,密闭容器内气体压强为,抽气过程中气体的温度不变,气体可视为理想气体,求:
(1)生肖摆件的密度;
(2)抽气10次后,密闭容器内剩余气体和抽气前气体质量的比值。
【参考答案】(1);(2)
【名师解析】(1)设生肖摆件的体积为,第一次抽气过程,
由玻意耳定律有
其中解得
生肖摆件的密度
(2)设第二次抽气后,容器内气体压强为,有
设第三次抽气后,容器内气体压强为,有
依次类推可知
设剩余气体压强为时体积为,则有
则剩余气体与抽气前气体的质量的比值为
5. (2024河南高考适应性考试)房间内温度升高空气外溢的过程可以抽象为如图所示的汽缸模型。汽缸内活塞可以无摩擦自由滑动,室内温度升高空气外溢,可视为空气膨胀推动活塞向外滑动。室内体积为V0,初始温度为T0。室内温度升高到T的过程中,活塞向外缓慢移至虚线位置。室内外气压始终恒定且相等,空气可视为理想气体。求
(1)汽缸内空气升温膨胀后的总体积V;
(2)升温前后室内空气质量之比。
【参考答案】(1);(2)
【名师解析】(1)由题知室内外气压始终恒定且相等,则由盖—吕萨克定律有
解得
(2)根据气体变化前后质量相等有ρ0V0 = ρV
解得
则升温前后室内空气质量之比为
6. (2024江西上进联盟质检)特斯拉公司的CEO埃隆·马斯克提出并推动了一项创新交通方式——马斯克“真空”隧道。其关键技术是在隧道内部创造接近真空的环境,列车在其中行驶时,所受空气阻力几乎为零,从而大幅提高列车的行驶速度。将马斯克隧道简化成如图所示模型,导热良好的密闭容器内封闭有压强为的空气,现用抽气筒缓慢从容器底部的阀门处(只出不进)进行抽气。已知抽气筒的抽气部分有效体积为密闭容器容积的,空气可视为理想气体,求:
(1)抽气两次后,容器内剩余空气的压强p;
(2)抽气次后,容器内剩余空气和抽出空气的质量之比k。
【参考答案】(1);(2)
【名师解析】
(1)根据题意,设容器的容积为,则每次抽气时可视为增加了的体积为,设第1次抽气后容器内剩余空气的压强为,则有
设第2次抽气后容器内剩余空气的压强为,则有
联立解得
(2)由(1)分析可知,抽气次后,容器内剩余空气的压强为
假设将容器内剩余气体等温压缩到压强为时的体积为,则有
容器内剩余空气和抽出空气的质量之比
联立解得
7.(8分)(2024年浙江省新阵地教育联盟质检)如图所示,一粗细均匀且一端密闭的细玻璃管开口向下竖直放置,管内有一段长为的水银柱,水银柱上方封闭了长度为的理想气体,此时封闭在管内的气体处于状态A,温度。先缓慢加热封闭气体使其处于状态B,此时封闭气体长度为。然后保持封闭气体温度不变,将玻璃管缓慢倒置后使气体达到状态C。已知大气压强恒为,求:
(1)判断气体从状态A到状态B的过程是吸热还是放热,并说明理由;
(2)气体处于状态B时的温度;
(3)气体处于状态C时的长度。
【名师解析】
(1)由热力学第一定律可知,从状态A到状态B,气体温度升高,内能增大(1分),同时对外做功(1分),所以气体一定吸热(1分)。
(2)设玻璃管横截面积为S,由盖-吕萨克定律(1分)
得(1分)
(3)气体处于状态B时,有
得
气体处于状态C时,有
得(1分)
由玻意耳定律(1分)
得(1分)
8. (2024武汉新洲区期末) 如图所示,开口向上竖直放置的玻璃管长为5h,质量为m、高为h的水银柱将一段空气柱封在管内,被封空气柱的温度为,水银柱上端到管口的距离为h。现给玻璃管加热,水银柱缓慢上升至管内剩余一半水银,此过程中空气柱的内能增加了,已知水银柱的截面积为S,大气压强为,重力加速度为g,忽略空气柱向外界传递的能量,求:
(1)水银柱上升至管口时,空气柱的温度T;
(2)水银柱上升过程中,空气柱需要吸收的热量Q。
【参考答案】(1);(2)
【名师解析】
(1)水银柱上升至管口时,封闭气体内部压强不变,皆为
因此对气体,为等压变化,有
解得
(2)在水银柱上升至管口时,空气柱对水银做功
在水银柱上升至管口并只剩下一半水银时,空气柱对水银做功
故整个过程,空气柱对水银做功为
根据热力学第一定律
解得
9. (2024江苏南京27中期末)在抗击新冠肺炎疫情期间,很多公共场所采用压缩式喷雾器来消毒。如图所示,喷雾器药液桶的总容积为V0,初始时,进液口和喷液口均关闭,桶内药液上方空气的压强为3p0,体积为。打开喷液口,喷洒消毒液,一段时间后关闭喷液口,此时药液桶内空气的强为2p0。不考虑打气筒与药液桶连接管内空气的体积,整个过程视为等温变化,大气压为标准大气压强p0。
(1)关闭喷液口时,已喷出消毒液体积是多少?
(2)每次打气,能打入压强为p0、体积为的空气,为了使药液桶内空气压强不小于3p0,至少需要打气多少次?
【参考答案】(1);(2)10次
【名师解析】
(1)已封闭气体为研究对象,由于气体发生等温变化,可知
解得
(2)等温变化可得
解得
次
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2024高考物理50热点冲刺训练
热点48 热学+液柱与变质量
1. (2024山东德州期末) 如图所示,10℃的氧气和20℃的氢气体积相同,汞柱在连通两容器的细管中央,下面的叙述中,正确的是( )
A. 当氧气和氢气的温度都升高10℃时,汞柱不移动
B. 当氧气和氢气的温度都升高10℃时,汞柱将向左移
C. 当氧气温度升高10℃,氢气温度升高20℃时,汞柱向左移
D. 当氧气温度升高10℃,氢气温度升高20℃时,汞柱不会移动
【参考答案】C
【名师解析】
假设两部分气体的体积不变,设气体初始状态的参量为p1、T1,末状态参量为p2、T2,变化温度为ΔT、变化压强为Δp,由查理定律有
可得
开始时两部分气体的压强p相同,若变化过程中ΔT相同,因为 T氧
得 Δp氧>Δp氢
所以汞柱向右移动,故AB错误。
开始时两部分气体的压强p相同,T氧=283K,T氢=293K,若ΔT氧=10K,ΔT氢=20K,由
得 Δp氧<Δp氢
所以汞柱向左移,故C正确,D错误。
2. (2024河北保定部分学校期末) 桶装纯净水及压水装置原理如图所示。柱形水桶直径为24cm,高为35cm;柱形压水气囊直径为6cm,高为8cm;水桶颈部的长度为10cm。当人用力向下压气囊时,气囊中的空气被压入桶内,桶内气体的压强增大,水通过细出水管流出。已知水桶所在处大气压强相当于10m高水柱产生的压强,当桶内的水还剩5cm高时,桶内气体的压强等于大气压强,忽略水桶颈部的体积。至少需要把气囊完全压下几次,才能有水从细出水管流出?(不考虑温度的变化)( )
A. 1次 B. 2次 C. 3次 D. 4次
【参考答案】C
【名师解析】
设大气压强为p0,水桶内气体体积为V0,气囊体积为V1,至少需要把气囊完全压下n次,桶内气体压强增加为p1,才能有水从细出水管流出,水桶内气体体积不变,温度不变,根据玻意耳定律可得
其中
联立解得
n=2.4
即至少需要把气囊完全压3次,故C正确,ABD错误。
3. (2024贵州高考适应性考试)下图是一个简易温度计示意图,左边由固定的玻璃球形容器和内径均匀且标有刻度的竖直玻璃管组成,右边是上端开口的柱形玻璃容器,左右两边通过软管连接,用水银将一定质量的空气封闭在左边容器中。已知球形容器的容积为,左边玻璃管内部的横截面积为。当环境温度为且左右液面平齐时,左管液面正好位于刻度处。设大气压强保持不变。
(1)当环境温度升高时,为使左右液面再次平齐,右边柱形容器应向上还向下移动?
(2)当液面位于刻度处且左右液面又一次平齐时,对应的环境温度是多少摄氏度?
【参考答案】(1)向下;(2)22℃
【名师解析】(1)当环境温度升高时,假设右边容器不动,则由于左侧气体体积变大,则右侧管中液面将高于左侧管中液面,则为使左右液面再次平齐,右边柱形容器应向下移动;
(2)开始时左侧气体体积
温度
当液面位于刻度处使气体的体积
气体进行等压变化,则根据盖吕萨克定律可得
解得
T2=295K
则
t2=T2-273℃=22℃
4.(12分)(2024年辽宁顶级名校质检)如图所示,小明用仪器测一质量为的生肖摆件的密度。已知密闭容器的容积为,抽气筒的容积为,把生肖摆件放入密闭容器,抽气筒与密闭容器通过单向阀门相连,活塞从抽气筒的左端向右移动到右端的过程中,阀门开启,密闭容器内的气体进入抽气筒,活塞从右端向左移动到左端过程中,阀门关闭,抽气筒内活塞左侧的气体被排出,完成一次抽气过程。开始时密闭容器内空气压强为,抽气一次后,密闭容器内气体压强为,抽气过程中气体的温度不变,气体可视为理想气体,求:
(1)生肖摆件的密度;
(2)抽气10次后,密闭容器内剩余气体和抽气前气体质量的比值。
【参考答案】(1);(2)
【名师解析】(1)设生肖摆件的体积为,第一次抽气过程,
由玻意耳定律有
其中解得
生肖摆件的密度
(2)设第二次抽气后,容器内气体压强为,有
设第三次抽气后,容器内气体压强为,有
依次类推可知
设剩余气体压强为时体积为,则有
则剩余气体与抽气前气体的质量的比值为
5. (2024河南高考适应性考试)房间内温度升高空气外溢的过程可以抽象为如图所示的汽缸模型。汽缸内活塞可以无摩擦自由滑动,室内温度升高空气外溢,可视为空气膨胀推动活塞向外滑动。室内体积为V0,初始温度为T0。室内温度升高到T的过程中,活塞向外缓慢移至虚线位置。室内外气压始终恒定且相等,空气可视为理想气体。求
(1)汽缸内空气升温膨胀后的总体积V;
(2)升温前后室内空气质量之比。
【参考答案】(1);(2)
【名师解析】(1)由题知室内外气压始终恒定且相等,则由盖—吕萨克定律有
解得
(2)根据气体变化前后质量相等有ρ0V0 = ρV
解得
则升温前后室内空气质量之比为
6. (2024江西上进联盟质检)特斯拉公司的CEO埃隆·马斯克提出并推动了一项创新交通方式——马斯克“真空”隧道。其关键技术是在隧道内部创造接近真空的环境,列车在其中行驶时,所受空气阻力几乎为零,从而大幅提高列车的行驶速度。将马斯克隧道简化成如图所示模型,导热良好的密闭容器内封闭有压强为的空气,现用抽气筒缓慢从容器底部的阀门处(只出不进)进行抽气。已知抽气筒的抽气部分有效体积为密闭容器容积的,空气可视为理想气体,求:
(1)抽气两次后,容器内剩余空气的压强p;
(2)抽气次后,容器内剩余空气和抽出空气的质量之比k。
【参考答案】(1);(2)
【名师解析】
(1)根据题意,设容器的容积为,则每次抽气时可视为增加了的体积为,设第1次抽气后容器内剩余空气的压强为,则有
设第2次抽气后容器内剩余空气的压强为,则有
联立解得
(2)由(1)分析可知,抽气次后,容器内剩余空气的压强为
假设将容器内剩余气体等温压缩到压强为时的体积为,则有
容器内剩余空气和抽出空气的质量之比
联立解得
7.(8分)(2024年浙江省新阵地教育联盟质检)如图所示,一粗细均匀且一端密闭的细玻璃管开口向下竖直放置,管内有一段长为的水银柱,水银柱上方封闭了长度为的理想气体,此时封闭在管内的气体处于状态A,温度。先缓慢加热封闭气体使其处于状态B,此时封闭气体长度为。然后保持封闭气体温度不变,将玻璃管缓慢倒置后使气体达到状态C。已知大气压强恒为,求:
(1)判断气体从状态A到状态B的过程是吸热还是放热,并说明理由;
(2)气体处于状态B时的温度;
(3)气体处于状态C时的长度。
【名师解析】
(1)由热力学第一定律可知,从状态A到状态B,气体温度升高,内能增大(1分),同时对外做功(1分),所以气体一定吸热(1分)。
(2)设玻璃管横截面积为S,由盖-吕萨克定律(1分)
得(1分)
(3)气体处于状态B时,有
得
气体处于状态C时,有
得(1分)
由玻意耳定律(1分)
得(1分)
8. (2024武汉新洲区期末) 如图所示,开口向上竖直放置的玻璃管长为5h,质量为m、高为h的水银柱将一段空气柱封在管内,被封空气柱的温度为,水银柱上端到管口的距离为h。现给玻璃管加热,水银柱缓慢上升至管内剩余一半水银,此过程中空气柱的内能增加了,已知水银柱的截面积为S,大气压强为,重力加速度为g,忽略空气柱向外界传递的能量,求:
(1)水银柱上升至管口时,空气柱的温度T;
(2)水银柱上升过程中,空气柱需要吸收的热量Q。
【参考答案】(1);(2)
【名师解析】
(1)水银柱上升至管口时,封闭气体内部压强不变,皆为
因此对气体,为等压变化,有
解得
(2)在水银柱上升至管口时,空气柱对水银做功
在水银柱上升至管口并只剩下一半水银时,空气柱对水银做功
故整个过程,空气柱对水银做功为
根据热力学第一定律
解得
9. (2024江苏南京27中期末)在抗击新冠肺炎疫情期间,很多公共场所采用压缩式喷雾器来消毒。如图所示,喷雾器药液桶的总容积为V0,初始时,进液口和喷液口均关闭,桶内药液上方空气的压强为3p0,体积为。打开喷液口,喷洒消毒液,一段时间后关闭喷液口,此时药液桶内空气的强为2p0。不考虑打气筒与药液桶连接管内空气的体积,整个过程视为等温变化,大气压为标准大气压强p0。
(1)关闭喷液口时,已喷出消毒液体积是多少?
(2)每次打气,能打入压强为p0、体积为的空气,为了使药液桶内空气压强不小于3p0,至少需要打气多少次?
【参考答案】(1);(2)10次
【名师解析】
(1)已封闭气体为研究对象,由于气体发生等温变化,可知
解得
(2)等温变化可得
解得
次
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
