鲁教版九年级数学上册第三章3.5确定二次函数的表达式(含答案)
文档属性
| 名称 | 鲁教版九年级数学上册第三章3.5确定二次函数的表达式(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 79.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-08 20:46:49 | ||
图片预览

文档简介
鲁教版九年级数学上册第三章3.5确定二次函数的表达式(含答案)
一、知识梳理
(1)如果给出二次函数图像上的三个点的坐标,或三组x,y的对应值,那么表达式设为一般式,即 。
(2)如果给出的条件涉及到二次函数的顶点坐标、对称轴或最大(小)值,那么表达式设为顶点式,即 。
(3)如果给出的条件涉及二次函数的图像与x轴的两个交点,可将表达式设为 ,即 。
二、典例精析
1、已知一个二次函数的图象经过A(﹣2,)、B(0,)和C(1,﹣2)三点.
(1)求出这个二次函数的解析式;
(2)若函数的图象与x轴相交于点E、F(E在F的左边),求△EFB的面积.
2、已知关于x的二次函数的图象的顶点坐标为(﹣1,2),且图象过点(1,﹣3),
(1)求这个二次函数的关系式;
(2)写出它的开口方向、对称轴.
3、如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
三、对应练习
4、已知二次函数y=x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(1,0),与y轴的交点坐标为(0,﹣3).
(1)求出b、c的值,并写出此二次函数的解析式;
(2)根据图象,直接写出函数值y为正数时,自变量x的取值范围.
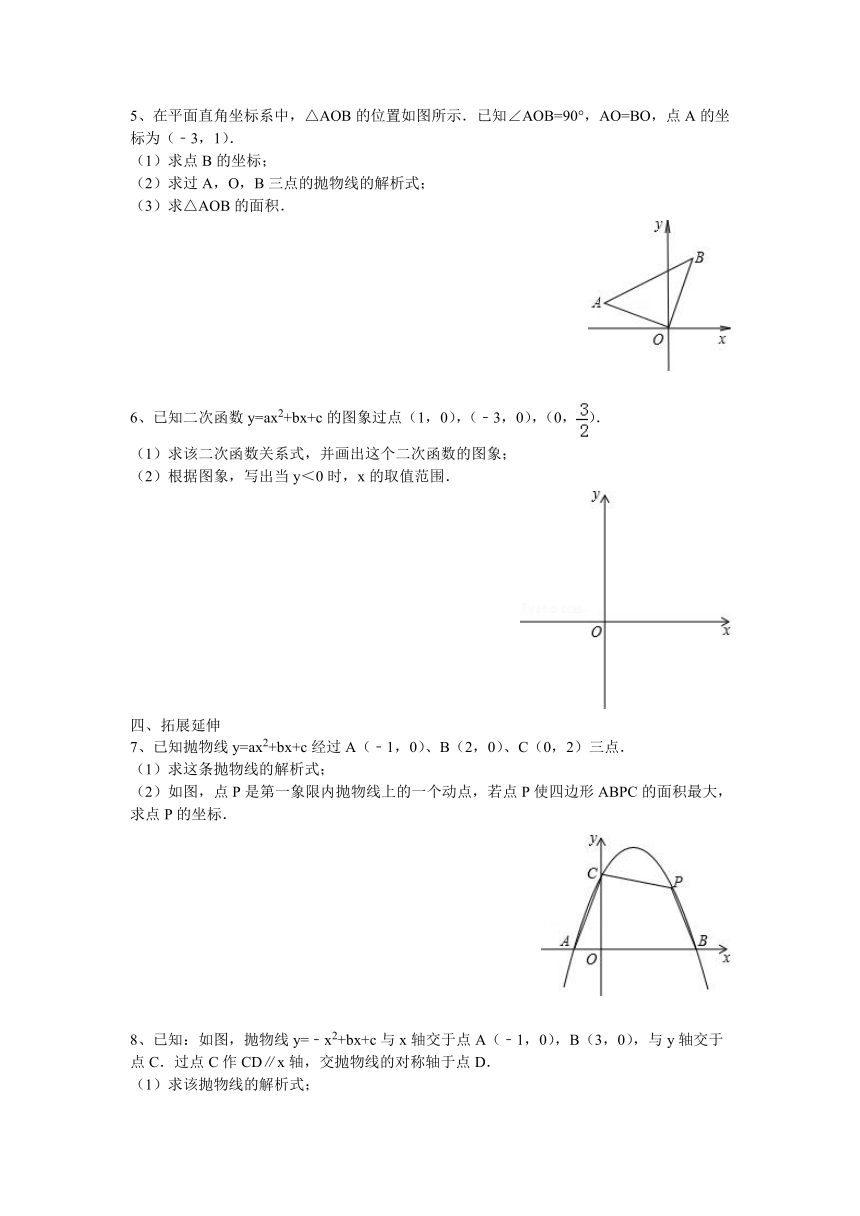
5、在平面直角坐标系中,△AOB的位置如图所示.已知∠AOB=90°,AO=BO,点A的坐标为(﹣3,1).
(1)求点B的坐标;
(2)求过A,O,B三点的抛物线的解析式;
(3)求△AOB的面积.
6、已知二次函数y=ax2+bx+c的图象过点(1,0),(﹣3,0),(0,).
(1)求该二次函数关系式,并画出这个二次函数的图象;
(2)根据图象,写出当y<0时,x的取值范围.
四、拓展延伸
7、已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(2,0)、C(0,2)三点.
(1)求这条抛物线的解析式;
(2)如图,点P是第一象限内抛物线上的一个动点,若点P使四边形ABPC的面积最大,求点P的坐标.
8、已知:如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.过点C作CD∥x轴,交抛物线的对称轴于点D.
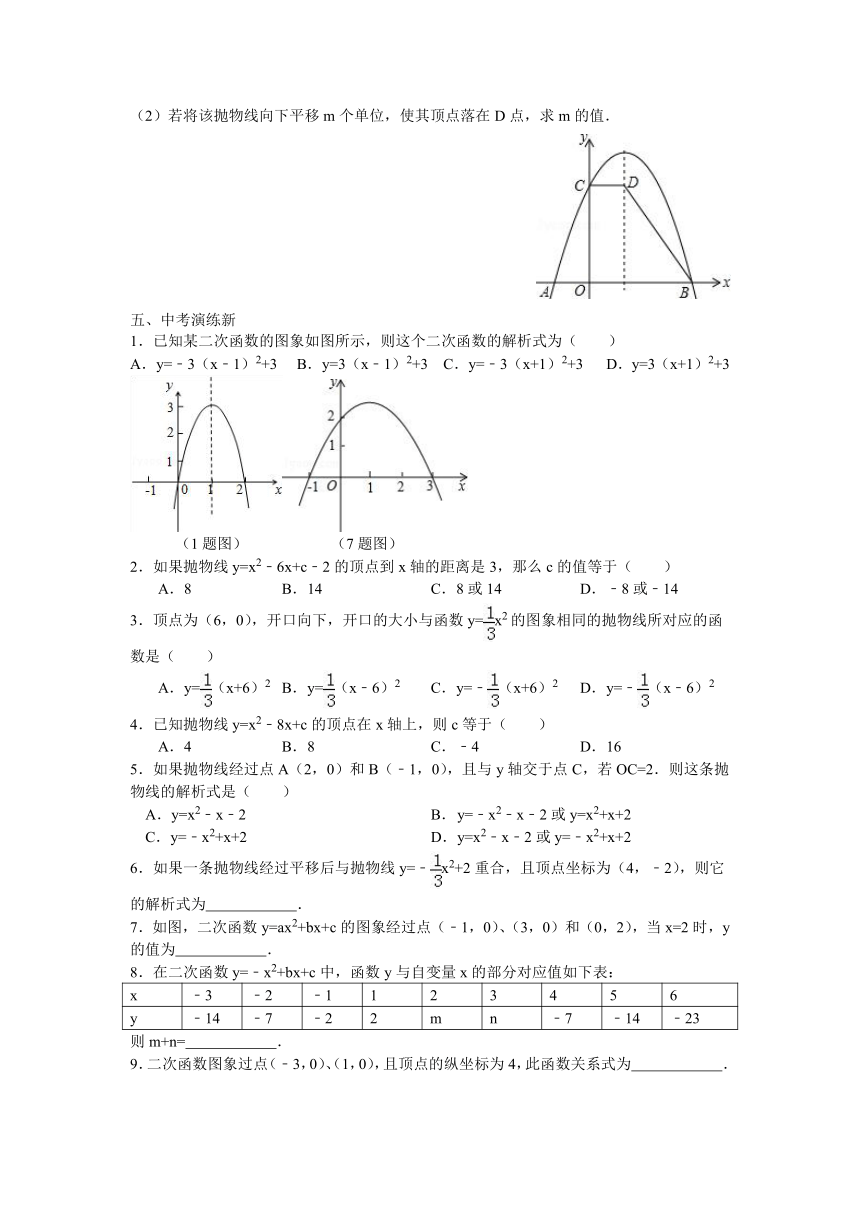
(1)求该抛物线的解析式;
(2)若将该抛物线向下平移m个单位,使其顶点落在D点,求m的值.
五、中考演练新
1.已知某二次函数的图象如图所示,则这个二次函数的解析式为( )
A.y=﹣3(x﹣1)2+3 B.y=3(x﹣1)2+3 C.y=﹣3(x+1)2+3 D.y=3(x+1)2+3
(1题图) (7题图)
2.如果抛物线y=x2﹣6x+c﹣2的顶点到x轴的距离是3,那么c的值等于( )
A.8 B. 14 C. 8或14 D. ﹣8或﹣14
3.顶点为(6,0),开口向下,开口的大小与函数y=x2的图象相同的抛物线所对应的函数是( )
A.y=(x+6)2 B. y=(x﹣6)2 C. y=﹣(x+6)2 D. y=﹣(x﹣6)2
4.已知抛物线y=x2﹣8x+c的顶点在x轴上,则c等于( )
A.4 B. 8 C. ﹣4 D. 16
5.如果抛物线经过点A(2,0)和B(﹣1,0),且与y轴交于点C,若OC=2.则这条抛物线的解析式是( )
A.y=x2﹣x﹣2 B. y=﹣x2﹣x﹣2或y=x2+x+2
C.y=﹣x2+x+2 D. y=x2﹣x﹣2或y=﹣x2+x+2
6.如果一条抛物线经过平移后与抛物线y=﹣x2+2重合,且顶点坐标为(4,﹣2),则它的解析式为 .
7.如图,二次函数y=ax2+bx+c的图象经过点(﹣1,0)、(3,0)和(0,2),当x=2时,y的值为 .
8.在二次函数y=﹣x2+bx+c中,函数y与自变量x的部分对应值如下表:
x ﹣3 ﹣2 ﹣1 1 2 3 4 5 6
y ﹣14 ﹣7 ﹣2 2 m n ﹣7 ﹣14 ﹣23
则m+n= .
9.二次函数图象过点(﹣3,0)、(1,0),且顶点的纵坐标为4,此函数关系式为 .
10.已知二次函数y=ax2+bx+c的图象经过A(﹣1,﹣1)、B(0,2)、C(1,3);则二次函数的解析式 .
11.已知抛物线的顶点坐标为M(1,﹣2),且经过点N(2,3),求此二次函数的解析式.
12.二次函数的图象经过点A(0,﹣3),B(2,﹣3),C(﹣1,0).
(1)求此二次函数的关系式;
(2)求此二次函数图象的顶点坐标;
(3)填空:把二次函数的图象沿坐标轴方向最少平移 5 个单位,使得该图象的顶点在原点.
13.已知二次函数y=ax2+bx+C图象上部分点的坐标(x,y)满足下表:
(1)求该二次函数的解析式;
(2)用配方法求出该二次函数图象的顶点坐标和对称轴.
x … ﹣2 ﹣1 0 1 …
y … 3 2 ﹣1 ﹣6 …
鲁教版九年级数学上册第三章3.5确定二次函数的表达式参考答案
1、解:(1)设二次函数的解析式为y=ax2+bx+c,
根据题意得,解得,所以二次函数解析式为y=x2﹣x﹣;
(2)当y=0时,x2﹣x﹣=0,解得x1=﹣1,x2=3,
所以E点坐标为(﹣1,0),F点坐标为(3,0),
所以△EFB的面积=×(3+1)×=3.
2、解:(1)设函数解析式为y=a(x﹣h)2+k,把顶点和点(1,﹣3)代入解析式,得:
a=﹣,所以抛物线的解析式为:;
(2)由(1)的函数解析式可得:抛物线的开口向下,对称轴x=﹣1.
3、 解:(1)∵抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,
∴方程x2+bx+c=0的两根为x=﹣1或x=3,∴﹣1+3=﹣b,﹣1×3=c,∴b=﹣2,c=﹣3,
∴二次函数解析式是y=x2﹣2x﹣3.
(2)∵y=﹣x2﹣2x﹣3=(x﹣1)2﹣4,∴抛物线的对称轴x=1,顶点坐标(1,﹣4).
(3)设P的纵坐标为|yP|,
∵S△PAB=8,∴AB |yP|=8,
∵AB=3+1=4,∴|yP|=4,∴yP=±4,
把yP=4代入解析式得,4=x2﹣2x﹣3,解得,x=1±2,
把yP=﹣4代入解析式得,﹣4=x2﹣2x﹣3,解得,x=1,
∴点P在该抛物线上滑动到(1+2,4)或(1﹣2,4)或(1,﹣4)时,满足S△PAB=8.
4、解:(1)由二次函数y=x2+bx+c的图象经过(1,0)和(0,﹣3)两点,
得,解这个方程组,得;∴抛物线的解析式为y=x2+2x﹣3.
(2)当x<﹣3或x>1时,y>0.
5、解:(1)如图,作AC⊥x轴,垂足为C,作BD⊥x轴垂足为D.
则∠ACO=∠ODB=90°,∴∠AOC+∠OAC=90°.
又∵∠AOB=90°,∴∠AOC+∠BOD=90°∴∠OAC=∠BOD.
又∵AO=BO,∴△ACO≌△ODB.∴OD=AC=1,DB=OC=3.
∴点B的坐标为(1,3).
(2)抛物线过原点,可设所求抛物线的解析式为:y=ax2+bx.
将A(﹣3,1),B(1,3),O(0,0)代入y=ax2+bx,得,解得.
故所求抛物线的解析式为y=x2+x.
(3)S△AOB=S梯形ACDB﹣S△AOC﹣S△BOD=×(1+3)×(1+3)﹣×3×1﹣×1×3
=8﹣﹣=8﹣3=5.
(5题图) (6题图)
6、解:(1)∵二次函数y=ax2+bx+c的图象过点(1,0),(﹣3,0),(0,),
∴,解得:,∴该二次函数关系式为:y=﹣x2﹣x+,
∵y=﹣x2﹣x+=﹣(x+1)2+2,
∴顶点为:(﹣1,2),
画出图象如上图:
(2)当y<0时,x的取值范围为:x<﹣3或x>1.
7、解:(1)∵抛物线y=ax2+bx+c经过A(﹣1,0)、B(2,0)、C(0,2)三点,
∴,解得:a=﹣1,b=1,c=2,∴这条抛物线的解析式为y=﹣x2+x+2.
(2)连接PO,过点P分别作PM⊥y轴于点M,PN⊥x轴于点N;
设点P坐标为(m,n),
则n=﹣m2+m+2;∵点P是第一象限内抛物线上的一个动点,
∴0<m<2,n>0;
由题意得:PM=m,PN=n;
∵,,,
∴S四边形ABPC=1+m+n=1+m﹣m2+m+2=﹣m2+2m+3,
∵二次项系数a=﹣1<0,
∴当m=时,四边形ABPC的面积取得最大值,
此时,n=﹣1+1+2=2;
∴当四边形ABPC的面积最大时,点P坐标为(1,2)
8、解:(1)将A(﹣1,0),B(3,0)代入y=﹣x2+bx+c中,
得:,解得:.则抛物线解析式为y=﹣x2+2x+3;
(2)当x=0,y=3,即OC=3,
∵抛物线解析式为y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点坐标为(1,4),
∵对称轴为直线,∴CD=1,
∵CD∥x轴,∴D(1,3),∴m=4﹣3=1.
中考演练部分
1.A 2.C 3.D 4.D 5.D
6.y=-(x-4)2-2 7.2 8.-1 9.y=-x2-2x+3 10.y=-x2+2x+2
11.解:已知抛物线的顶点坐标为M(1,﹣2),
设此二次函数的解析式为y=a(x﹣1)2﹣2,
把点(2,3)代入解析式,得:
a﹣2=3,即a=5,
∴此函数的解析式为y=5(x﹣1)2﹣2.
12.解:(1)设y=ax2+bx﹣3,
把点(2,﹣3),(﹣1,0)代入得,解方程组得∴y=x2﹣2x﹣3;
(也可设y=a(x﹣1)2+k)
(2)y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴函数的顶点坐标为(1,﹣4);
(3)|1﹣0|+|﹣4﹣0|=5.
13.解:(1)把点(0,﹣1)代入y=ax2+bx+c,得c=﹣1.
再把点(﹣1,2),(1,﹣6)分别代入y=ax2+bx﹣1中,得
,解得:,所以这个二次函数的关系式为:y=﹣x2﹣4x﹣1.
(2)y=﹣x2﹣4x﹣1
=﹣(x+2)2﹣5.
该二次函数图象的顶点坐标为(﹣2,﹣5),对称轴为x=﹣2.
一、知识梳理
(1)如果给出二次函数图像上的三个点的坐标,或三组x,y的对应值,那么表达式设为一般式,即 。
(2)如果给出的条件涉及到二次函数的顶点坐标、对称轴或最大(小)值,那么表达式设为顶点式,即 。
(3)如果给出的条件涉及二次函数的图像与x轴的两个交点,可将表达式设为 ,即 。
二、典例精析
1、已知一个二次函数的图象经过A(﹣2,)、B(0,)和C(1,﹣2)三点.
(1)求出这个二次函数的解析式;
(2)若函数的图象与x轴相交于点E、F(E在F的左边),求△EFB的面积.
2、已知关于x的二次函数的图象的顶点坐标为(﹣1,2),且图象过点(1,﹣3),
(1)求这个二次函数的关系式;
(2)写出它的开口方向、对称轴.
3、如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
三、对应练习
4、已知二次函数y=x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(1,0),与y轴的交点坐标为(0,﹣3).
(1)求出b、c的值,并写出此二次函数的解析式;
(2)根据图象,直接写出函数值y为正数时,自变量x的取值范围.
5、在平面直角坐标系中,△AOB的位置如图所示.已知∠AOB=90°,AO=BO,点A的坐标为(﹣3,1).
(1)求点B的坐标;
(2)求过A,O,B三点的抛物线的解析式;
(3)求△AOB的面积.
6、已知二次函数y=ax2+bx+c的图象过点(1,0),(﹣3,0),(0,).
(1)求该二次函数关系式,并画出这个二次函数的图象;
(2)根据图象,写出当y<0时,x的取值范围.
四、拓展延伸
7、已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(2,0)、C(0,2)三点.
(1)求这条抛物线的解析式;
(2)如图,点P是第一象限内抛物线上的一个动点,若点P使四边形ABPC的面积最大,求点P的坐标.
8、已知:如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.过点C作CD∥x轴,交抛物线的对称轴于点D.
(1)求该抛物线的解析式;
(2)若将该抛物线向下平移m个单位,使其顶点落在D点,求m的值.
五、中考演练新
1.已知某二次函数的图象如图所示,则这个二次函数的解析式为( )
A.y=﹣3(x﹣1)2+3 B.y=3(x﹣1)2+3 C.y=﹣3(x+1)2+3 D.y=3(x+1)2+3
(1题图) (7题图)
2.如果抛物线y=x2﹣6x+c﹣2的顶点到x轴的距离是3,那么c的值等于( )
A.8 B. 14 C. 8或14 D. ﹣8或﹣14
3.顶点为(6,0),开口向下,开口的大小与函数y=x2的图象相同的抛物线所对应的函数是( )
A.y=(x+6)2 B. y=(x﹣6)2 C. y=﹣(x+6)2 D. y=﹣(x﹣6)2
4.已知抛物线y=x2﹣8x+c的顶点在x轴上,则c等于( )
A.4 B. 8 C. ﹣4 D. 16
5.如果抛物线经过点A(2,0)和B(﹣1,0),且与y轴交于点C,若OC=2.则这条抛物线的解析式是( )
A.y=x2﹣x﹣2 B. y=﹣x2﹣x﹣2或y=x2+x+2
C.y=﹣x2+x+2 D. y=x2﹣x﹣2或y=﹣x2+x+2
6.如果一条抛物线经过平移后与抛物线y=﹣x2+2重合,且顶点坐标为(4,﹣2),则它的解析式为 .
7.如图,二次函数y=ax2+bx+c的图象经过点(﹣1,0)、(3,0)和(0,2),当x=2时,y的值为 .
8.在二次函数y=﹣x2+bx+c中,函数y与自变量x的部分对应值如下表:
x ﹣3 ﹣2 ﹣1 1 2 3 4 5 6
y ﹣14 ﹣7 ﹣2 2 m n ﹣7 ﹣14 ﹣23
则m+n= .
9.二次函数图象过点(﹣3,0)、(1,0),且顶点的纵坐标为4,此函数关系式为 .
10.已知二次函数y=ax2+bx+c的图象经过A(﹣1,﹣1)、B(0,2)、C(1,3);则二次函数的解析式 .
11.已知抛物线的顶点坐标为M(1,﹣2),且经过点N(2,3),求此二次函数的解析式.
12.二次函数的图象经过点A(0,﹣3),B(2,﹣3),C(﹣1,0).
(1)求此二次函数的关系式;
(2)求此二次函数图象的顶点坐标;
(3)填空:把二次函数的图象沿坐标轴方向最少平移 5 个单位,使得该图象的顶点在原点.
13.已知二次函数y=ax2+bx+C图象上部分点的坐标(x,y)满足下表:
(1)求该二次函数的解析式;
(2)用配方法求出该二次函数图象的顶点坐标和对称轴.
x … ﹣2 ﹣1 0 1 …
y … 3 2 ﹣1 ﹣6 …
鲁教版九年级数学上册第三章3.5确定二次函数的表达式参考答案
1、解:(1)设二次函数的解析式为y=ax2+bx+c,
根据题意得,解得,所以二次函数解析式为y=x2﹣x﹣;
(2)当y=0时,x2﹣x﹣=0,解得x1=﹣1,x2=3,
所以E点坐标为(﹣1,0),F点坐标为(3,0),
所以△EFB的面积=×(3+1)×=3.
2、解:(1)设函数解析式为y=a(x﹣h)2+k,把顶点和点(1,﹣3)代入解析式,得:
a=﹣,所以抛物线的解析式为:;
(2)由(1)的函数解析式可得:抛物线的开口向下,对称轴x=﹣1.
3、 解:(1)∵抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,
∴方程x2+bx+c=0的两根为x=﹣1或x=3,∴﹣1+3=﹣b,﹣1×3=c,∴b=﹣2,c=﹣3,
∴二次函数解析式是y=x2﹣2x﹣3.
(2)∵y=﹣x2﹣2x﹣3=(x﹣1)2﹣4,∴抛物线的对称轴x=1,顶点坐标(1,﹣4).
(3)设P的纵坐标为|yP|,
∵S△PAB=8,∴AB |yP|=8,
∵AB=3+1=4,∴|yP|=4,∴yP=±4,
把yP=4代入解析式得,4=x2﹣2x﹣3,解得,x=1±2,
把yP=﹣4代入解析式得,﹣4=x2﹣2x﹣3,解得,x=1,
∴点P在该抛物线上滑动到(1+2,4)或(1﹣2,4)或(1,﹣4)时,满足S△PAB=8.
4、解:(1)由二次函数y=x2+bx+c的图象经过(1,0)和(0,﹣3)两点,
得,解这个方程组,得;∴抛物线的解析式为y=x2+2x﹣3.
(2)当x<﹣3或x>1时,y>0.
5、解:(1)如图,作AC⊥x轴,垂足为C,作BD⊥x轴垂足为D.
则∠ACO=∠ODB=90°,∴∠AOC+∠OAC=90°.
又∵∠AOB=90°,∴∠AOC+∠BOD=90°∴∠OAC=∠BOD.
又∵AO=BO,∴△ACO≌△ODB.∴OD=AC=1,DB=OC=3.
∴点B的坐标为(1,3).
(2)抛物线过原点,可设所求抛物线的解析式为:y=ax2+bx.
将A(﹣3,1),B(1,3),O(0,0)代入y=ax2+bx,得,解得.
故所求抛物线的解析式为y=x2+x.
(3)S△AOB=S梯形ACDB﹣S△AOC﹣S△BOD=×(1+3)×(1+3)﹣×3×1﹣×1×3
=8﹣﹣=8﹣3=5.
(5题图) (6题图)
6、解:(1)∵二次函数y=ax2+bx+c的图象过点(1,0),(﹣3,0),(0,),
∴,解得:,∴该二次函数关系式为:y=﹣x2﹣x+,
∵y=﹣x2﹣x+=﹣(x+1)2+2,
∴顶点为:(﹣1,2),
画出图象如上图:
(2)当y<0时,x的取值范围为:x<﹣3或x>1.
7、解:(1)∵抛物线y=ax2+bx+c经过A(﹣1,0)、B(2,0)、C(0,2)三点,
∴,解得:a=﹣1,b=1,c=2,∴这条抛物线的解析式为y=﹣x2+x+2.
(2)连接PO,过点P分别作PM⊥y轴于点M,PN⊥x轴于点N;
设点P坐标为(m,n),
则n=﹣m2+m+2;∵点P是第一象限内抛物线上的一个动点,
∴0<m<2,n>0;
由题意得:PM=m,PN=n;
∵,,,
∴S四边形ABPC=1+m+n=1+m﹣m2+m+2=﹣m2+2m+3,
∵二次项系数a=﹣1<0,
∴当m=时,四边形ABPC的面积取得最大值,
此时,n=﹣1+1+2=2;
∴当四边形ABPC的面积最大时,点P坐标为(1,2)
8、解:(1)将A(﹣1,0),B(3,0)代入y=﹣x2+bx+c中,
得:,解得:.则抛物线解析式为y=﹣x2+2x+3;
(2)当x=0,y=3,即OC=3,
∵抛物线解析式为y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点坐标为(1,4),
∵对称轴为直线,∴CD=1,
∵CD∥x轴,∴D(1,3),∴m=4﹣3=1.
中考演练部分
1.A 2.C 3.D 4.D 5.D
6.y=-(x-4)2-2 7.2 8.-1 9.y=-x2-2x+3 10.y=-x2+2x+2
11.解:已知抛物线的顶点坐标为M(1,﹣2),
设此二次函数的解析式为y=a(x﹣1)2﹣2,
把点(2,3)代入解析式,得:
a﹣2=3,即a=5,
∴此函数的解析式为y=5(x﹣1)2﹣2.
12.解:(1)设y=ax2+bx﹣3,
把点(2,﹣3),(﹣1,0)代入得,解方程组得∴y=x2﹣2x﹣3;
(也可设y=a(x﹣1)2+k)
(2)y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴函数的顶点坐标为(1,﹣4);
(3)|1﹣0|+|﹣4﹣0|=5.
13.解:(1)把点(0,﹣1)代入y=ax2+bx+c,得c=﹣1.
再把点(﹣1,2),(1,﹣6)分别代入y=ax2+bx﹣1中,得
,解得:,所以这个二次函数的关系式为:y=﹣x2﹣4x﹣1.
(2)y=﹣x2﹣4x﹣1
=﹣(x+2)2﹣5.
该二次函数图象的顶点坐标为(﹣2,﹣5),对称轴为x=﹣2.
