1.1计数原理2
图片预览




文档简介
课件13张PPT。例1:用0,1,2,3,4,5这六个数字,
(1)可以组成多少个数字无重复的四位数?(2)可以组成多少个数字无重复的四位偶数?
一、排数字问题
二、映射个数问题例2、若集合A={a1,a2,a3,a4,a5},
B={b1,b2},从集合A到集合B可建立 个不同
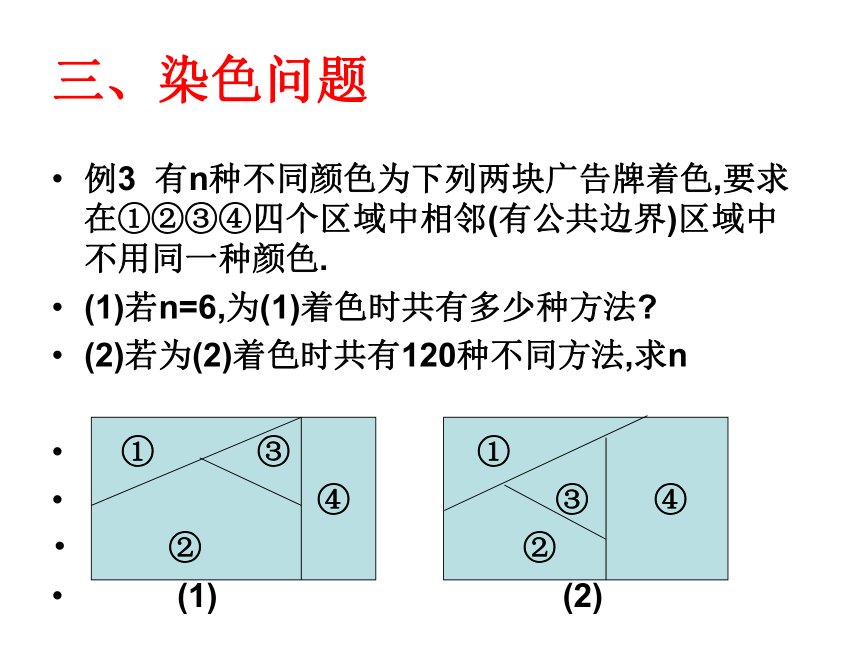
的映射,从B到A可建立 个不同的映射。 三、染色问题例3 有n种不同颜色为下列两块广告牌着色,要求在①②③④四个区域中相邻(有公共边界)区域中不用同一种颜色.
(1)若n=6,为(1)着色时共有多少种方法?
(2)若为(2)着色时共有120种不同方法,求n
① ③ ①
④ ③ ④
② ②
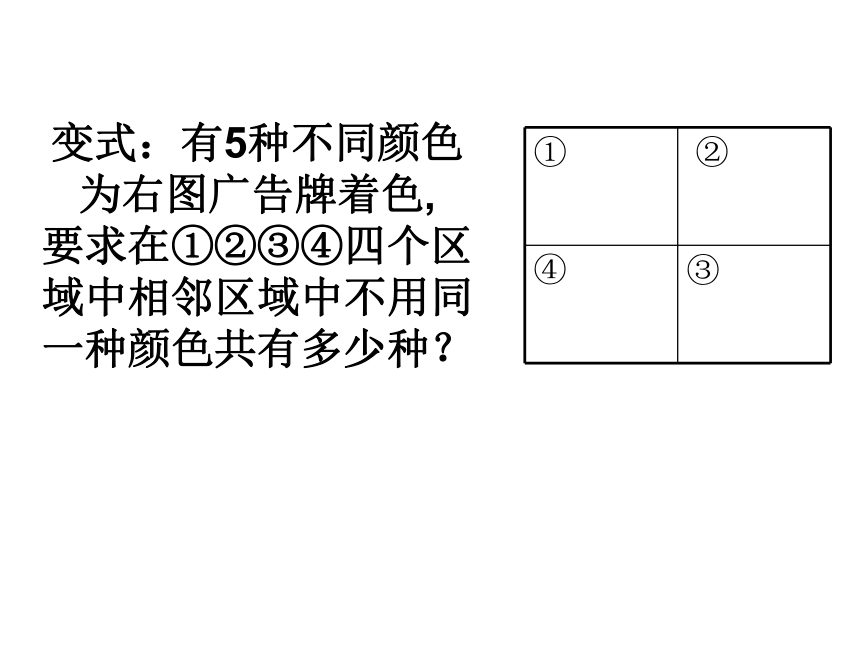
(1) (2) 变式:有5种不同颜色为右图广告牌着色,
要求在①②③④四个区域中相邻区域中不用同一种颜色共有多少种?四、综合问题例4已知二次函数 若
则可以得到多少个不同的二次函数?其中图象过原点的二次函数有多少个?图象过原点且顶点在第一象限的二次函数又有多少个?例5 :乘积
展开后共有几项?变式:乘积
展开后共有几项?变式:乘积
展开后至多有几项?合并同类项后至多有几项?课堂练习1、8本不同的书,任选3本分给3个同学,每人1本,有多少种不同的分法?
2、将4封信投入3个不同的邮箱,有多少种不同的投法?
3、已知
则方程 可表示不同的圆的个数有多少?4、如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4条路,从丙地到丁地有2条路。从甲地到丁地共有多少种不同地走法?N1=2×3=6N2=4×2=8N= N1+N2 =145、如图,该电路,从A到B共有多少条不同的线路可通电?AB解: 从总体上看由A到B的通电线路可分三类,
第一类, m1 = 3 条
第二类, m2 = 1 条
第三类, m3 = 2×2 = 4 条
所以, 根据分类原理, 从A到B共有
N = 3 + 1 + 4 = 8
条不同的线路可通电。
在解题有时既要分类又要分步。6、用1,5,9,13中的任意一个数作分子,4,8,12,16中的任意一个数作分母,可构成多少个不同的分数?可构成多少个不同的真分数?7、 五名学生报名参加四项体育比赛,每人限报一项,报名方法的种数为多少?他们争夺这四项比赛的冠军,获得冠军的可能性有多少种? 课堂小结 运用分类加法计数原理与分步乘法计数原理的注意点:
分类加法计数原理:首先确定分类标准,其次满足:完成这件事的任何一种方法必属某一类,并且分别属于不同的两类的方法都是不同的方法,即“不重不漏”。
分步乘法计数原理:首先确定分步标准,其次满足:必须并且只需连续完成这n个步骤,这件事才算完成。即“步骤完整”。
B={b1,b2},从集合A到集合B可建立 个不同
的映射,从B到A可建立 个不同的映射。 三、染色问题例3 有n种不同颜色为下列两块广告牌着色,要求在①②③④四个区域中相邻(有公共边界)区域中不用同一种颜色.
(1)若n=6,为(1)着色时共有多少种方法?
(2)若为(2)着色时共有120种不同方法,求n
① ③ ①
④ ③ ④
② ②
(1) (2) 变式:有5种不同颜色为右图广告牌着色,
要求在①②③④四个区域中相邻区域中不用同一种颜色共有多少种?四、综合问题例4已知二次函数 若
则可以得到多少个不同的二次函数?其中图象过原点的二次函数有多少个?图象过原点且顶点在第一象限的二次函数又有多少个?例5 :乘积
展开后共有几项?变式:乘积
展开后共有几项?变式:乘积
展开后至多有几项?合并同类项后至多有几项?课堂练习1、8本不同的书,任选3本分给3个同学,每人1本,有多少种不同的分法?
2、将4封信投入3个不同的邮箱,有多少种不同的投法?
3、已知
则方程 可表示不同的圆的个数有多少?4、如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4条路,从丙地到丁地有2条路。从甲地到丁地共有多少种不同地走法?N1=2×3=6N2=4×2=8N= N1+N2 =145、如图,该电路,从A到B共有多少条不同的线路可通电?AB解: 从总体上看由A到B的通电线路可分三类,
第一类, m1 = 3 条
第二类, m2 = 1 条
第三类, m3 = 2×2 = 4 条
所以, 根据分类原理, 从A到B共有
N = 3 + 1 + 4 = 8
条不同的线路可通电。
在解题有时既要分类又要分步。6、用1,5,9,13中的任意一个数作分子,4,8,12,16中的任意一个数作分母,可构成多少个不同的分数?可构成多少个不同的真分数?7、 五名学生报名参加四项体育比赛,每人限报一项,报名方法的种数为多少?他们争夺这四项比赛的冠军,获得冠军的可能性有多少种? 课堂小结 运用分类加法计数原理与分步乘法计数原理的注意点:
分类加法计数原理:首先确定分类标准,其次满足:完成这件事的任何一种方法必属某一类,并且分别属于不同的两类的方法都是不同的方法,即“不重不漏”。
分步乘法计数原理:首先确定分步标准,其次满足:必须并且只需连续完成这n个步骤,这件事才算完成。即“步骤完整”。
