/2.1.2离散型随机变量及其分布列(一)
文档属性
| 名称 | /2.1.2离散型随机变量及其分布列(一) |

|
|
| 格式 | rar | ||
| 文件大小 | 221.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-05-29 00:00:00 | ||
图片预览


文档简介
课件11张PPT。问题:抛掷一枚骰子,所得的点数X有哪些值?
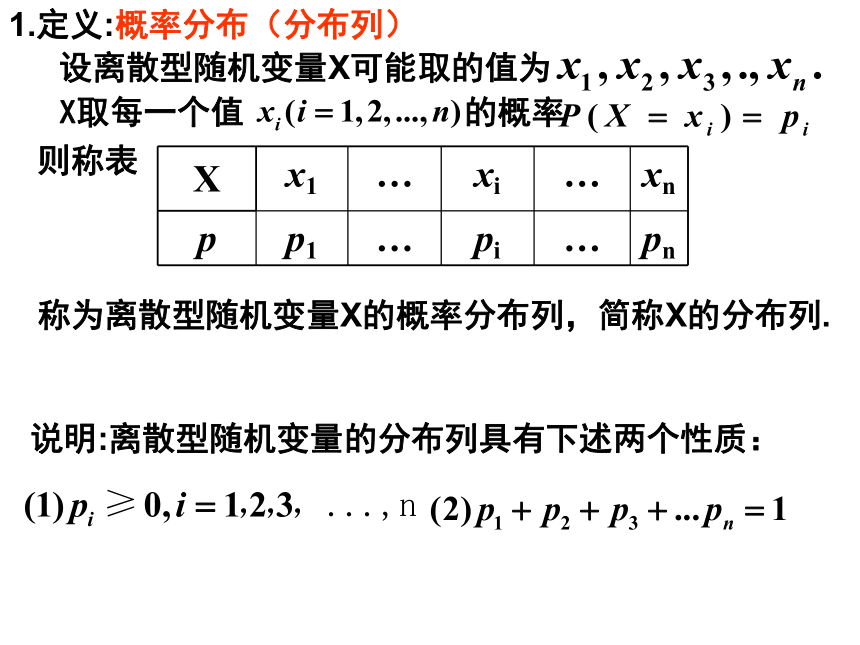
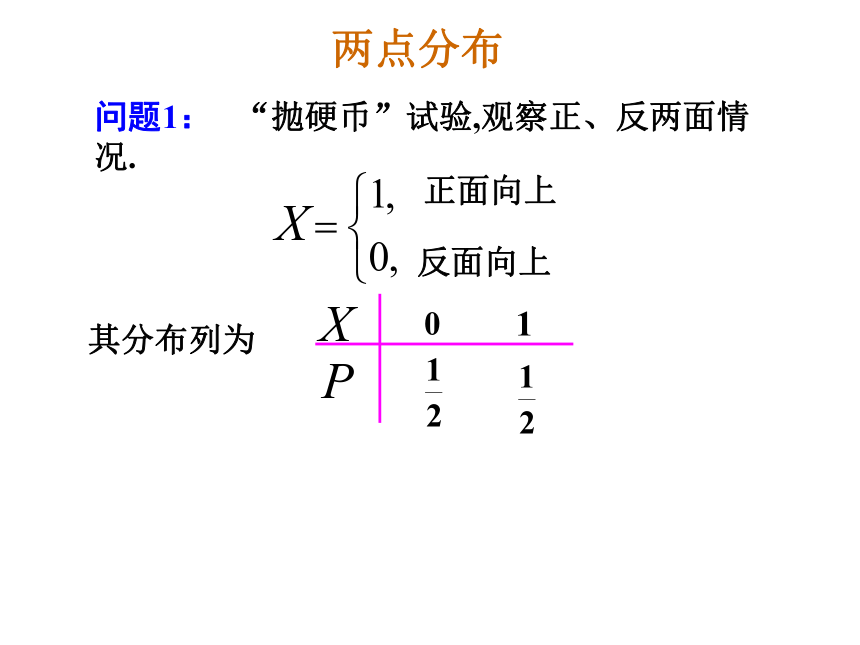
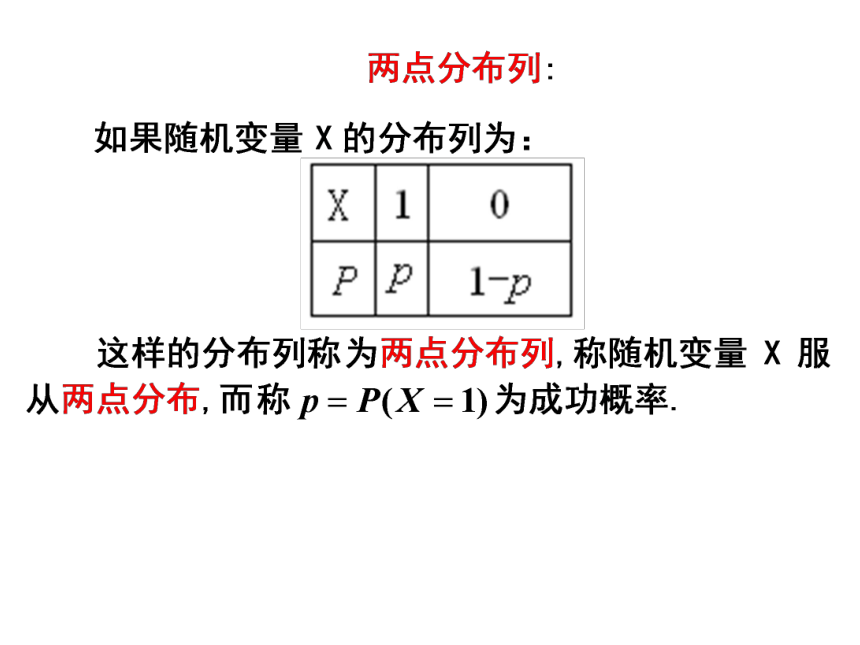
X取每个值的概率是多少? 则而且列出了 的每一个取值的概率.该表不仅列出了随机变量 的所有取值.列成表的形式1.求{X<3}的概率分布列2.求{X为偶数}的概率 X取每一个值 的概率 称为离散型随机变量X的概率分布列,简称X的分布列.则称表设离散型随机变量X可能取的值为1.定义:概率分布(分布列)说明:离散型随机变量的分布列具有下述两个性质:问题1: “抛硬币”试验,观察正、反两面情况. 其分布列为两点分布练习: 200件产品中,有190件合格品,10件不合格品,现从中随机抽取一件, 若规定则随机变量 服从(0 —1)分布. 两点分布是最简单的一种分布,任何一个只有两种可能结果的随机现象, 比如新生婴儿是男还是女、明天是否下雨、种籽是否发芽等, 都属于两点分布.说明练习1.随机变量ξ的分布列为解:(1)由离散型随机变量的分布列的性质得(1)求常数a;(2)求P(1<ξ<4)(2)P(1<ξ<4)=P(ξ=2)+P(ξ=3)=0.12+0.3=0.42课后练习1,2且相应取值的概率没有变化练习2:已知随机变量 的分布列如下:-2-13210求出随机变量的分布列.思考1.一个口袋里有5只球,编号为1,2,3,4,5,在袋中同时取出3只,以ξ表示取出的3个球中的最小号码,试写出ξ的分布列. 解: 随机变量ξ的可取值为 1,2,3.P(ξ=1)= =3/5;同理可得 P(ξ=2)=3/10;P(ξ=3)=1/10. 因此,ξ的分布列如下表所示课堂练习:2.设随机变量 的分布列为则 的值为 .1.设随机变量 的分布列如下:4321则 的值为 .3.设随机变量 的分布列为则 ( )A、1B、C、D、4.设随机变量 只能取5、6、7、···、16这12个值,且取每一个值的概率均相等,则 ,若 则实数 的取值范围是 .D
X取每个值的概率是多少? 则而且列出了 的每一个取值的概率.该表不仅列出了随机变量 的所有取值.列成表的形式1.求{X<3}的概率分布列2.求{X为偶数}的概率 X取每一个值 的概率 称为离散型随机变量X的概率分布列,简称X的分布列.则称表设离散型随机变量X可能取的值为1.定义:概率分布(分布列)说明:离散型随机变量的分布列具有下述两个性质:问题1: “抛硬币”试验,观察正、反两面情况. 其分布列为两点分布练习: 200件产品中,有190件合格品,10件不合格品,现从中随机抽取一件, 若规定则随机变量 服从(0 —1)分布. 两点分布是最简单的一种分布,任何一个只有两种可能结果的随机现象, 比如新生婴儿是男还是女、明天是否下雨、种籽是否发芽等, 都属于两点分布.说明练习1.随机变量ξ的分布列为解:(1)由离散型随机变量的分布列的性质得(1)求常数a;(2)求P(1<ξ<4)(2)P(1<ξ<4)=P(ξ=2)+P(ξ=3)=0.12+0.3=0.42课后练习1,2且相应取值的概率没有变化练习2:已知随机变量 的分布列如下:-2-13210求出随机变量的分布列.思考1.一个口袋里有5只球,编号为1,2,3,4,5,在袋中同时取出3只,以ξ表示取出的3个球中的最小号码,试写出ξ的分布列. 解: 随机变量ξ的可取值为 1,2,3.P(ξ=1)= =3/5;同理可得 P(ξ=2)=3/10;P(ξ=3)=1/10. 因此,ξ的分布列如下表所示课堂练习:2.设随机变量 的分布列为则 的值为 .1.设随机变量 的分布列如下:4321则 的值为 .3.设随机变量 的分布列为则 ( )A、1B、C、D、4.设随机变量 只能取5、6、7、···、16这12个值,且取每一个值的概率均相等,则 ,若 则实数 的取值范围是 .D
