6.4平面向量的应用知识梳理+同步练习(含答案) 2023-2024学年高一下学期人教A版(2019)数学必修第二册
文档属性
| 名称 | 6.4平面向量的应用知识梳理+同步练习(含答案) 2023-2024学年高一下学期人教A版(2019)数学必修第二册 |  | |
| 格式 | docx | ||
| 文件大小 | 708.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-03 18:16:18 | ||
图片预览



文档简介
6.4平面向量的应用
学校:___________姓名:___________班级:___________考号:___________
1. 向量方法解决平面几何问题的步骤:首先,需要建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题。然后,通过向量运算,研究几何元素之间的关系,如距离、夹角等问题。最后,把运算结果“翻译”成几何关系。
2. 向量在物理中的应用:在物理问题中,常见的向量包括力、速度、加速度、位移等。向量的加减法运算体现在这些物理量的合成与分解中。
此外,平面向量的应用还可能涉及到余弦定理等数学知识。例如,由余弦定理,我们可以得到cosA=b +2cb c-a ,cosB=c +等推论。
一、单选题
1.如图所示,C、D、A三点在同一水平线上,AB是塔的中轴线,在C、D两处测得塔顶部B处的仰角分别是和,如果C、D间的距离是a,测角仪高为b,则塔高为
A. B.
C. D.
2.在中,a,b,c分别是角A,B,C的对边,若,则的值为( )
A.2021 B.2022 C.2023 D.2024
3.在锐角三角形中,、、的对边分别为、、,且满足,则的取值范围为( )
A. B.
C. D.
4.在△中,,则=( )
A.± B. C.- D.
5.在中,内角A,B,C的对边分别为a,b,c.,则( )
A.120° B.150° C.45° D.60°
6.△的三个内角,,所对的边分别为,,,且a=1,B=45°,其面积为2,则△的外接圆的直径为( )
A. B. C.4 D.5
7.在中,若,则是( )
A.直角三角形 B.等腰三角形
C.等腰或直角三角形 D.等腰直角三角形
8.在中,,,,则的面积为( )
A.24 B.18 C.12 D.9
9.锐角中,角,,的对边分别为,,,若,则的取值范围是( )
A. B. C. D.
10.如图,在四边形中,已知,,,点在边上,则的最小值为( )
A. B. C. D.
11.在△ABC中,角A,B,C的对边分别为a,b,c,若(a+b)(sinA﹣sinB)=c(sinC+sinB),则∠A=( )
A. B. C. D.
12.在中,角所对的边分别是,已知,,,则( )
A. B. C. D.
二、填空题
13.在中,,,分别是角,,的对边,若,,,则的面积为 .
14.需要测量某塔的高度,选取与塔底在同一个水平面内的两个测量基点与,现测得,,米,在点处测得塔顶的仰角为,则塔高为 米
15.在△中,角的对边为,若,则 .
16.在等腰中,,边上的中线长为6,则当的面积取得最大值时,的长为 .
17.在中,内角所对的边分别为,若,,,则 .
三、解答题
18.若ABC的内角A,B,C所对的边分别为a,b,c,且满足,
(1)求值:
(2)从下列条件①,条件②,条件③三个条件中选择一个作为已知,求的值,
条件①若;
条件②若;
条件③若
19.请从①;②;③这三个条件中任选一个,补充在下面问题中,并加以解答(如未作出选择,则按照选择①评分.选择的编号请填写到答题卡对应位置上)
在△ABC中,a,b,c分别是角A,B,C的对边,若___________,
(1)求角B的大小;
(2)若△ABC为锐角三角形,,求的取值范围.
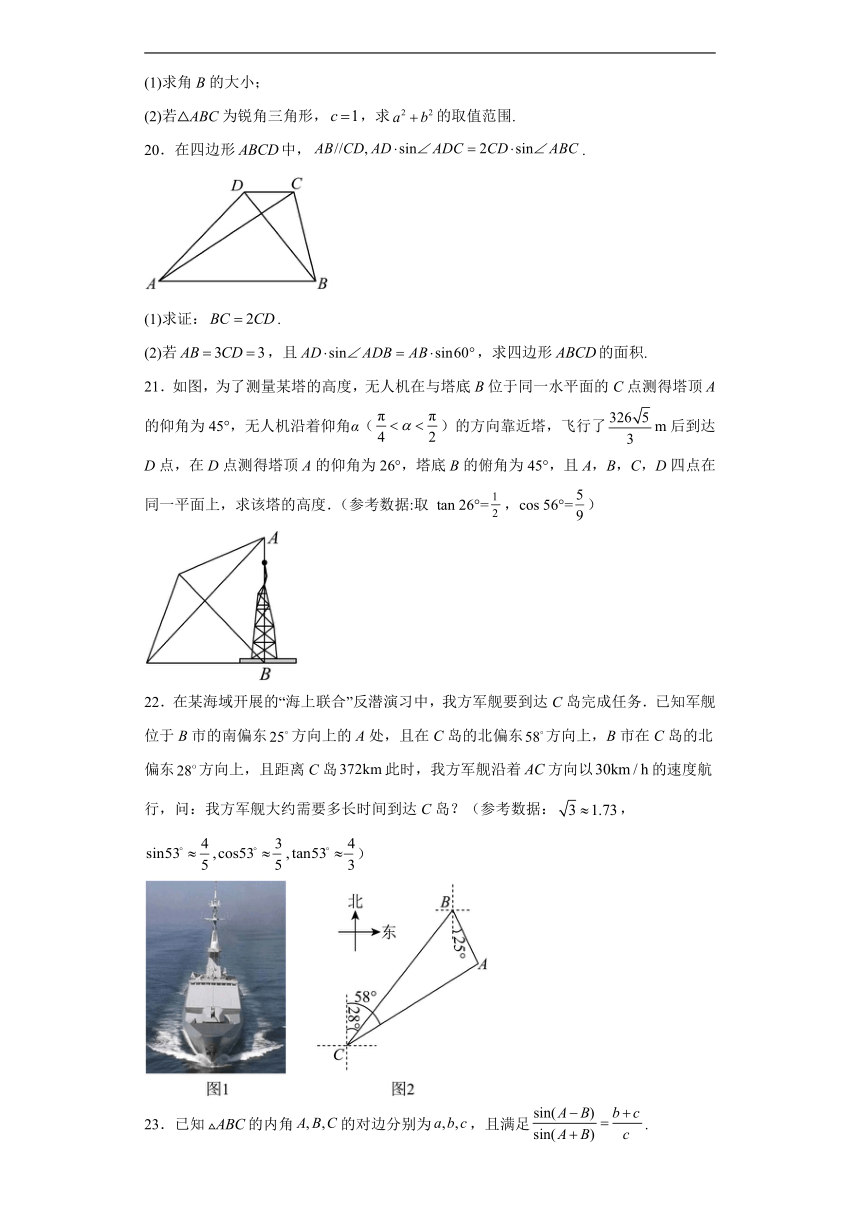
20.在四边形中,.
(1)求证:.
(2)若,且,求四边形的面积.
21.如图,为了测量某塔的高度,无人机在与塔底B位于同一水平面的C点测得塔顶A的仰角为45°,无人机沿着仰角α()的方向靠近塔,飞行了m后到达D点,在D点测得塔顶A的仰角为26°,塔底B的俯角为45°,且A,B,C,D四点在同一平面上,求该塔的高度.(参考数据:取 tan 26°=,cos 56°=)
22.在某海域开展的“海上联合”反潜演习中,我方军舰要到达C岛完成任务.已知军舰位于B市的南偏东方向上的A处,且在C岛的北偏东方向上,B市在C岛的北偏东方向上,且距离C岛此时,我方军舰沿着方向以的速度航行,问:我方军舰大约需要多长时间到达C岛?(参考数据:,)
23.已知的内角的对边分别为,且满足.
(1)求角的大小;
(2)当时,求面积的最大值,并指出面积最大时的形状.
参考答案:
1.A
2.B
3.D
4.A
5.C
6.B
7.B
8.C
9.B
10.A
11.A
12.A
13.
14.
15.
16.
17.
18.(1)1
(2)略
19.(1)
(2)
20.(1)略
(2)若,则四边形的面积,
若,则四边形的面积.
21.326m
22.10小时
23.(1);(2)有最大值,此时为等腰三角形.
学校:___________姓名:___________班级:___________考号:___________
1. 向量方法解决平面几何问题的步骤:首先,需要建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题。然后,通过向量运算,研究几何元素之间的关系,如距离、夹角等问题。最后,把运算结果“翻译”成几何关系。
2. 向量在物理中的应用:在物理问题中,常见的向量包括力、速度、加速度、位移等。向量的加减法运算体现在这些物理量的合成与分解中。
此外,平面向量的应用还可能涉及到余弦定理等数学知识。例如,由余弦定理,我们可以得到cosA=b +2cb c-a ,cosB=c +等推论。
一、单选题
1.如图所示,C、D、A三点在同一水平线上,AB是塔的中轴线,在C、D两处测得塔顶部B处的仰角分别是和,如果C、D间的距离是a,测角仪高为b,则塔高为
A. B.
C. D.
2.在中,a,b,c分别是角A,B,C的对边,若,则的值为( )
A.2021 B.2022 C.2023 D.2024
3.在锐角三角形中,、、的对边分别为、、,且满足,则的取值范围为( )
A. B.
C. D.
4.在△中,,则=( )
A.± B. C.- D.
5.在中,内角A,B,C的对边分别为a,b,c.,则( )
A.120° B.150° C.45° D.60°
6.△的三个内角,,所对的边分别为,,,且a=1,B=45°,其面积为2,则△的外接圆的直径为( )
A. B. C.4 D.5
7.在中,若,则是( )
A.直角三角形 B.等腰三角形
C.等腰或直角三角形 D.等腰直角三角形
8.在中,,,,则的面积为( )
A.24 B.18 C.12 D.9
9.锐角中,角,,的对边分别为,,,若,则的取值范围是( )
A. B. C. D.
10.如图,在四边形中,已知,,,点在边上,则的最小值为( )
A. B. C. D.
11.在△ABC中,角A,B,C的对边分别为a,b,c,若(a+b)(sinA﹣sinB)=c(sinC+sinB),则∠A=( )
A. B. C. D.
12.在中,角所对的边分别是,已知,,,则( )
A. B. C. D.
二、填空题
13.在中,,,分别是角,,的对边,若,,,则的面积为 .
14.需要测量某塔的高度,选取与塔底在同一个水平面内的两个测量基点与,现测得,,米,在点处测得塔顶的仰角为,则塔高为 米
15.在△中,角的对边为,若,则 .
16.在等腰中,,边上的中线长为6,则当的面积取得最大值时,的长为 .
17.在中,内角所对的边分别为,若,,,则 .
三、解答题
18.若ABC的内角A,B,C所对的边分别为a,b,c,且满足,
(1)求值:
(2)从下列条件①,条件②,条件③三个条件中选择一个作为已知,求的值,
条件①若;
条件②若;
条件③若
19.请从①;②;③这三个条件中任选一个,补充在下面问题中,并加以解答(如未作出选择,则按照选择①评分.选择的编号请填写到答题卡对应位置上)
在△ABC中,a,b,c分别是角A,B,C的对边,若___________,
(1)求角B的大小;
(2)若△ABC为锐角三角形,,求的取值范围.
20.在四边形中,.
(1)求证:.
(2)若,且,求四边形的面积.
21.如图,为了测量某塔的高度,无人机在与塔底B位于同一水平面的C点测得塔顶A的仰角为45°,无人机沿着仰角α()的方向靠近塔,飞行了m后到达D点,在D点测得塔顶A的仰角为26°,塔底B的俯角为45°,且A,B,C,D四点在同一平面上,求该塔的高度.(参考数据:取 tan 26°=,cos 56°=)
22.在某海域开展的“海上联合”反潜演习中,我方军舰要到达C岛完成任务.已知军舰位于B市的南偏东方向上的A处,且在C岛的北偏东方向上,B市在C岛的北偏东方向上,且距离C岛此时,我方军舰沿着方向以的速度航行,问:我方军舰大约需要多长时间到达C岛?(参考数据:,)
23.已知的内角的对边分别为,且满足.
(1)求角的大小;
(2)当时,求面积的最大值,并指出面积最大时的形状.
参考答案:
1.A
2.B
3.D
4.A
5.C
6.B
7.B
8.C
9.B
10.A
11.A
12.A
13.
14.
15.
16.
17.
18.(1)1
(2)略
19.(1)
(2)
20.(1)略
(2)若,则四边形的面积,
若,则四边形的面积.
21.326m
22.10小时
23.(1);(2)有最大值,此时为等腰三角形.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
