第六章平面向量及其应用知识梳理+同步练习(含答案) 2023-2024学年高一下学期人教A版(2019)数学必修第二册
文档属性
| 名称 | 第六章平面向量及其应用知识梳理+同步练习(含答案) 2023-2024学年高一下学期人教A版(2019)数学必修第二册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-03 18:16:40 | ||
图片预览

文档简介
第六章平面向量及其应用
学校:___________姓名:___________班级:___________考号:___________
1. 向量的基本概念:向量是既有大小又有方向的量。数量则只有大小,没有方向。有向线段的三要素包括起点、方向和长度。零向量是长度为0的向量,其方向是任意的,所有的零向量都相等。单位向量是长度等于1个单位的向量。平行向量(也称为共线向量)是方向相同或相反的非零向量,零向量与任一向量都平行。相等向量是指长度相等且方向相同的向量。
2. 向量加法运算:向量加法运算有两种法则,即三角形法则和平行四边形法则。三角形法则的特点是首尾相连,而平行四边形法则的特点是共起点。向量加法运算满足交换律和结合律。此外,还可以进行坐标运算。
3. 向量减法运算:向量减法运算的特点是共起点,连终点,方向指向被减向量。同样,也可以进行坐标运算。
4. 向量数乘运算:实数与向量的积是一个向量的运算,叫做向量的数乘。
一、单选题
1.已知向量,其中且,则=( )
A.0 B.
C.2 D.
2.若向量且则=( )
A.3 B.5 C. D.
3.在中,已知,则的取值范围为( )
A. B. C. D.
4.已知的重心为点,点为上一点,且满足,记,则( )
A. B. C. D.
5.在中,角A,B,C的对边分别为a,b,c,,则角C的大小为( )
A. B. C. D.
6.在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD交于点F,若,,则
A. B. C. D.
7.已知向量,则“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
8.已知是的外心,,,则( )
A.10 B.9 C.8 D.6
9.在中,内角,,的对边分别为 ,若,,,则的值为( )
A. B. C. D.
10.已知点是边长为2的正的内部(不包括边界)的一个点,则的取值范围为( )
A. B. C. D.
11.已知中,其内角A,B,C的对边分别为a,b,c,下列命题正确的有( )
A.若为等边三角形且边长为2,则
B.若“”是“”的充分不必要条件
C.若满足,则
D.若,则为锐角三角形
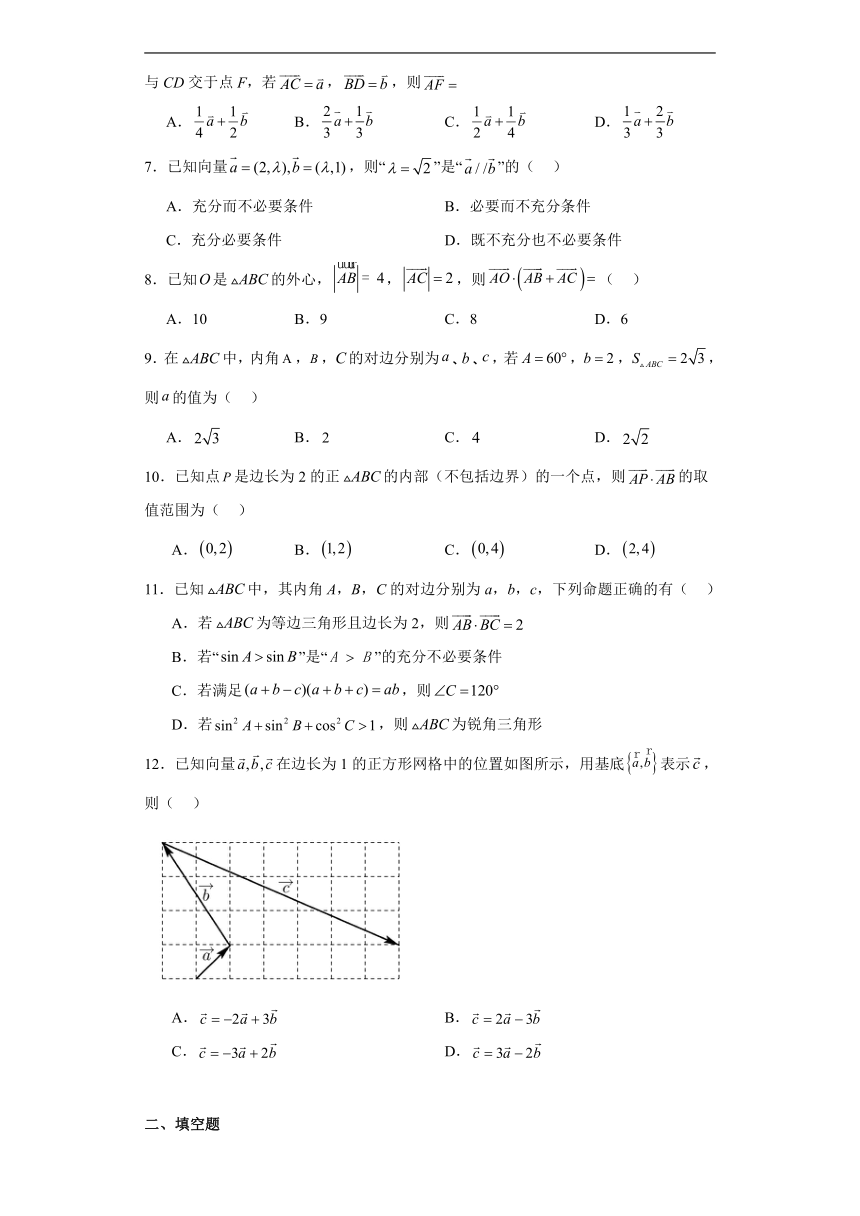
12.已知向量在边长为1的正方形网格中的位置如图所示,用基底表示,则( )
A. B.
C. D.
二、填空题
13.若平面向量满足,则 .
14.在中,,则角的最大值为 (结果用反三角形式表示).
15.已知,是与向量方向相同的单位向量,向量在向量上的投影向量为,则与的夹角为
16.已知的内角A、B、C的对边分别为a、b、c,,则一定为 三角形.
17.已知向量,,.若,则 .
三、解答题
18.(1)化简:.
(2)已知向量为,未知向量为向量,满足关系式,求向量.
19.已知向量,,.
(1)画出函数的图象;
(2)在△ABC中,BC=,sin B=3sin C,若,求△ABC的周长.
20.求证:顺次连接任意凸四边形各边中点,构成一个平行四边形.
21.如图,为了测量某塔的高度,无人机在与塔底B位于同一水平面的C点测得塔顶A的仰角为45°,无人机沿着仰角α()的方向靠近塔,飞行了m后到达D点,在D点测得塔顶A的仰角为26°,塔底B的俯角为45°,且A,B,C,D四点在同一平面上,求该塔的高度.(参考数据:取 tan 26°=,cos 56°=)
22.在某海域开展的“海上联合”反潜演习中,我方军舰要到达C岛完成任务.已知军舰位于B市的南偏东方向上的A处,且在C岛的北偏东方向上,B市在C岛的北偏东方向上,且距离C岛此时,我方军舰沿着方向以的速度航行,问:我方军舰大约需要多长时间到达C岛?(参考数据:,)
23.如图,在平面四边形中,已知,,,点在上且,,.
(1)求的值:
(2)求的面积.
参考答案:
1.B
2.C
3.C
4.A
5.A
6.B
7.A
8.A
9.A
10.C
11.C
12.D
13.
14.
15./
16.等腰
17./
18.(1) ;(2) ,.
19.(1)略;(2).
20.略
21.326m
22.10小时
23.(1)
(2)
学校:___________姓名:___________班级:___________考号:___________
1. 向量的基本概念:向量是既有大小又有方向的量。数量则只有大小,没有方向。有向线段的三要素包括起点、方向和长度。零向量是长度为0的向量,其方向是任意的,所有的零向量都相等。单位向量是长度等于1个单位的向量。平行向量(也称为共线向量)是方向相同或相反的非零向量,零向量与任一向量都平行。相等向量是指长度相等且方向相同的向量。
2. 向量加法运算:向量加法运算有两种法则,即三角形法则和平行四边形法则。三角形法则的特点是首尾相连,而平行四边形法则的特点是共起点。向量加法运算满足交换律和结合律。此外,还可以进行坐标运算。
3. 向量减法运算:向量减法运算的特点是共起点,连终点,方向指向被减向量。同样,也可以进行坐标运算。
4. 向量数乘运算:实数与向量的积是一个向量的运算,叫做向量的数乘。
一、单选题
1.已知向量,其中且,则=( )
A.0 B.
C.2 D.
2.若向量且则=( )
A.3 B.5 C. D.
3.在中,已知,则的取值范围为( )
A. B. C. D.
4.已知的重心为点,点为上一点,且满足,记,则( )
A. B. C. D.
5.在中,角A,B,C的对边分别为a,b,c,,则角C的大小为( )
A. B. C. D.
6.在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD交于点F,若,,则
A. B. C. D.
7.已知向量,则“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
8.已知是的外心,,,则( )
A.10 B.9 C.8 D.6
9.在中,内角,,的对边分别为 ,若,,,则的值为( )
A. B. C. D.
10.已知点是边长为2的正的内部(不包括边界)的一个点,则的取值范围为( )
A. B. C. D.
11.已知中,其内角A,B,C的对边分别为a,b,c,下列命题正确的有( )
A.若为等边三角形且边长为2,则
B.若“”是“”的充分不必要条件
C.若满足,则
D.若,则为锐角三角形
12.已知向量在边长为1的正方形网格中的位置如图所示,用基底表示,则( )
A. B.
C. D.
二、填空题
13.若平面向量满足,则 .
14.在中,,则角的最大值为 (结果用反三角形式表示).
15.已知,是与向量方向相同的单位向量,向量在向量上的投影向量为,则与的夹角为
16.已知的内角A、B、C的对边分别为a、b、c,,则一定为 三角形.
17.已知向量,,.若,则 .
三、解答题
18.(1)化简:.
(2)已知向量为,未知向量为向量,满足关系式,求向量.
19.已知向量,,.
(1)画出函数的图象;
(2)在△ABC中,BC=,sin B=3sin C,若,求△ABC的周长.
20.求证:顺次连接任意凸四边形各边中点,构成一个平行四边形.
21.如图,为了测量某塔的高度,无人机在与塔底B位于同一水平面的C点测得塔顶A的仰角为45°,无人机沿着仰角α()的方向靠近塔,飞行了m后到达D点,在D点测得塔顶A的仰角为26°,塔底B的俯角为45°,且A,B,C,D四点在同一平面上,求该塔的高度.(参考数据:取 tan 26°=,cos 56°=)
22.在某海域开展的“海上联合”反潜演习中,我方军舰要到达C岛完成任务.已知军舰位于B市的南偏东方向上的A处,且在C岛的北偏东方向上,B市在C岛的北偏东方向上,且距离C岛此时,我方军舰沿着方向以的速度航行,问:我方军舰大约需要多长时间到达C岛?(参考数据:,)
23.如图,在平面四边形中,已知,,,点在上且,,.
(1)求的值:
(2)求的面积.
参考答案:
1.B
2.C
3.C
4.A
5.A
6.B
7.A
8.A
9.A
10.C
11.C
12.D
13.
14.
15./
16.等腰
17./
18.(1) ;(2) ,.
19.(1)略;(2).
20.略
21.326m
22.10小时
23.(1)
(2)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
