2023-2024学年人教版八年级数学下册第十七章 勾股定理 单元同步检测试题(含答案)
文档属性
| 名称 | 2023-2024学年人教版八年级数学下册第十七章 勾股定理 单元同步检测试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 320.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-03 00:00:00 | ||
图片预览




文档简介
第十七章《勾股定理》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每小题3分,共30分)
1.下列各组数中,能作为直角三角形三边长的是( )
A.4,5,6 B.5,7,12 C.3,5, D.1,,
2.如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,则AB的长为( )
A.2 B.3 C.2 D.2
A.10km B.12km C.13km D.26km
2题图 4题图 5题图 6题图
3.一直角三角形的斜边长比其中一直角边长大3,另一直角边长为9,则斜边长为( )
A.15 B.12 C.10 D.9
4.如图,在边长为1个单位长度的小正方形网格中,点A、B都是格点(即网格线的交点),则线段AB的长度为( )
A.3 B.5 C.6 D.4
5.如图,Rt△ABC中,∠ABC=90°,∠BAC=30°,AC=2,分别以三边为直径画半圆,则两个月形图案的面积之和(阴影部分的面积)是( )
A. B.π C. D.
6.我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边长分别为a、b,那么(a﹣b)2的值是( )
A.1 B.2 C.12 D.13
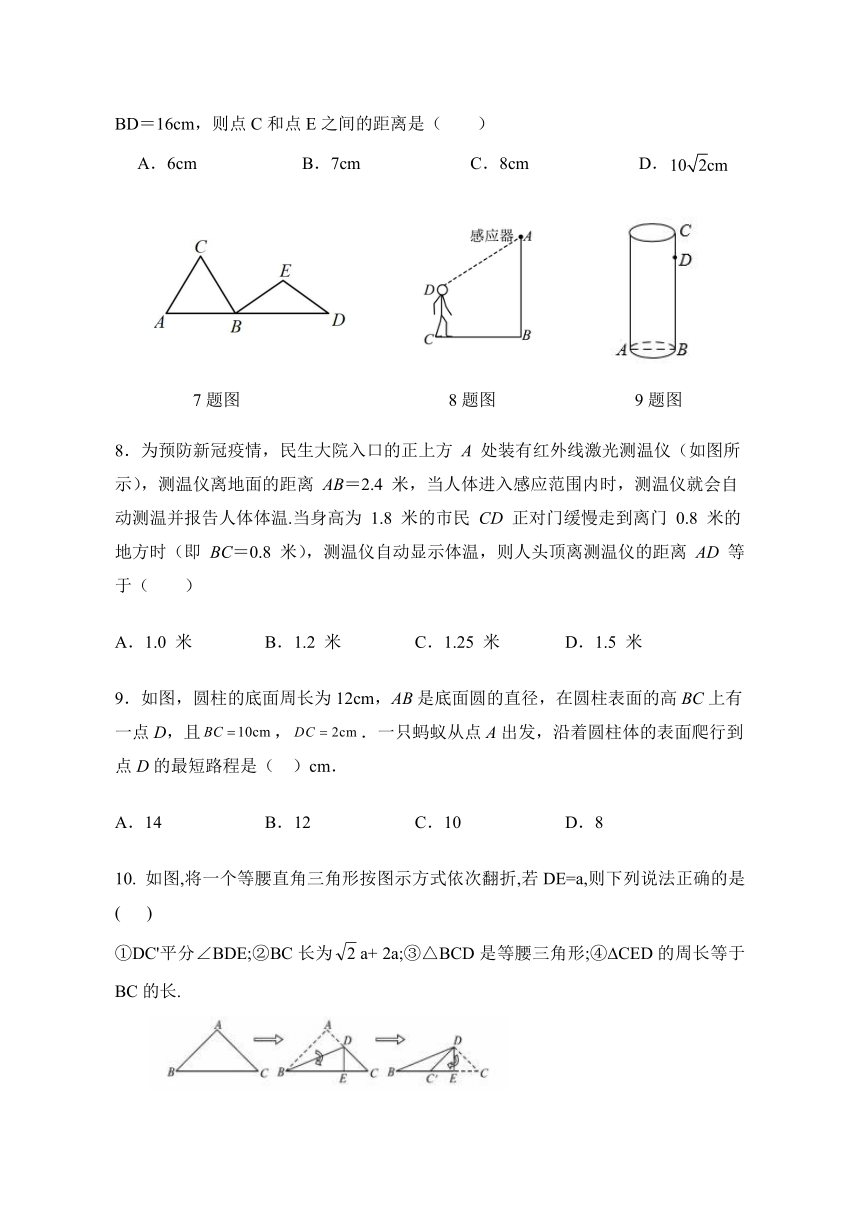
7.如图,AC=BC=BE=DE=10cm,点A、B、D在同一条直线上,AB=12cm,BD=16cm,则点C和点E之间的距离是( )
A.6cm B.7cm C.8cm D.
7题图 8题图 9题图
8.为预防新冠疫情,民生大院入口的正上方 A 处装有红外线激光测温仪(如图所示),测温仪离地面的距离 AB=2.4 米,当人体进入感应范围内时,测温仪就会自动测温并报告人体体温.当身高为 1.8 米的市民 CD 正对门缓慢走到离门 0.8 米的地方时(即 BC=0.8 米),测温仪自动显示体温,则人头顶离测温仪的距离 AD 等于( )
A.1.0 米 B.1.2 米 C.1.25 米 D.1.5 米
9.如图,圆柱的底面周长为12cm,AB是底面圆的直径,在圆柱表面的高BC上有一点D,且,.一只蚂蚁从点A出发,沿着圆柱体的表面爬行到点D的最短路程是( )cm.
A.14 B.12 C.10 D.8
10. 如图,将一个等腰直角三角形按图示方式依次翻折,若DE=a,则下列说法正确的是( )
①DC'平分∠BDE;②BC长为a+ 2a;③△BCD是等腰三角形;④ CED的周长等于BC的长.
A.①②③ B.②④ C.②③④ D.③④
二、填空题(每题3分,共24分)
11.写出命题“如果a=b,那么3a=3b”的逆命题: .
12. 已知的三边长分别是6,8,10,则的面积是__________.
13. 已知一个三角形的三边长为5,12,13,则此三角形最长边上的高=________.
14. 如图,数轴上点A所表示的实数是______.
14题图 15题图
15.如图,在Rt△ABC中,∠ACB=90°,D是△ABC内的一个动点,满足AC2﹣AD2=CD2.若AB=2,BC=4,则BD长的最小值为 .
16.如今人们锻炼身体的意识日渐增强,但是发现少数人保护环境的意识仍显淡薄,应提醒注意.如图是房山某公园的一角,有人为了抄近道而避开路的拐角∠ABC(∠ABC=90°),于是在草坪内走出了一条不该有的“捷径路AC”.已知AB=30米,BC=40米,他们踩坏了 米的草坪,只为少走 米的路.
16题图 17题图
17.甲、乙两艘客轮分别用和速度同时离开港口,甲、乙客轮分别都用到达A、B两点,若A,B两点的直线距离为,甲客轮沿着北偏东的方向航行,则乙客轮的航行方向可能是___________.(只填序号)
①北偏西 ②南偏西 ③南偏东 ④南偏西
18.如图,在中,,且周长为,点从点开始,沿边向点以每秒的速度移动;点从点开始,沿边向点以每秒的速度移动.若同时出发,则过秒时,的面积为___________.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.如图,在△ABC中,,于点D,,,.请求出△ABC的面积和CD的长.
2.湖的两岸有A,B两棵景观树,数学兴趣小组设计实验测量两棵景观树之间的距离,他们在与AB垂直的BC方向上取点C,测得米,米.
求:(1)两棵景观树之间的距离;
(2)点B到直线AC的距离.
21.已知与互为相反数,且a,b为一元二次方程的两个实数根.
(1)求c、m的值;
(2)试判断以a、b、c为三边的三角形的形状,并说明理由.
22.如图,在一笔直的海岸线上有相距的、两个观测站,站在站的正东方向上,从站测得船在北偏东的方向上,从站测得船在东北方向上,则船到海岸线的距离是多少?
23.如图,将直角三角形分割成一个正方形和两对全等的直角三角形,直角三角形ABC中,∠ACB=90°,BC=a,AC=b,AB=c,正方形IECF中,IE=EC=CF=FI=x
(1)小明发明了求正方形边长的方法:
由题意可得BD=BE=a﹣x,AD=AF=b﹣x
因为AB=BD+AD,所以a﹣x+b﹣x=c,解得x=
(2)小亮也发现了另一种求正方形边长的方法:
利用S△ABC=S△AIB+S△AIC+S△BIC可以得到x与a、b、c的关系,请根据小亮的思路完成他的求解过程:
(3)请结合小明和小亮得到的结论验证勾股定理.
24.为了积极响应国家新农村建设,遂宁市某镇政府采用了移动宣讲的形式进行宣传动员.如图,笔直公路MN的一侧点A处有一村庄,村庄A到公路MN的距离为600米,假使宣讲车P周围1000米以内能听到广播宣传,宣讲车P在公路MN上沿PN方向行驶时:
(1)请问村庄能否听到宣传,请说明理由;
(2)如果能听到,已知宣讲车的速度是200米/分钟,那么村庄总共能听到多长时间的宣传?
参考答案
一.选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 C C A B A A A A D A
二.填空题:
11.如果3a=3b,那么a=b
12.答案:7
13.答案:
14.答案:2米
15.【解答】解:取AC的中点H,连接HD,HB,
在Rt△ABC中,由勾股定理得AC,
∵AC2﹣AD2=CD2.
∴∠ADC=90°,
∵点H为AC的中点,
∴DH=CH=3,
∴BH,
∵BD≥BH﹣DH,
∴BD的最小值为5﹣3=2,
故答案为:2.
16.【解答】解:在Rt△ABC中,∵AB=30米,BC=40米,
∴AC50,30+40﹣50=20(米),
∴他们踩坏了50米的草坪,只为少走20米的路.
故答案为:50,20.
17.【解答】解:∵正方形A、B的边长分别为1和2,
∴SA=1,SB=4,
∵正方形A、B、C的边长分别为直角三角形的三边长,
∴SA+SC=SB,
∴SC=4﹣1=3.
故答案为:3.
17.③
18.18
三.解答题:
19.△ABC的面积为,CD的长为cm
20.(1)A,B两点间的 距离是40米;(2)点B到直线AC的距离是24米.
21.(1),;
(2)等腰直角三角形,理由见解析
【解析】
(1)利用互为相反数的两个数的和等于0求得a+b,c,然后利用根与系数关系即可求解;
(2)将,代入 ,解方程求得与的值,然后利用勾股定理的逆定理即可求解.
(1)
∵与互为相反数,
∴
∴
∵a,b为一元二次方程的两个实数根
∴由根与系数的关系可知,
解得,;
(2)
等腰直角三角形,理由如下:
将,代入 ,
即
解得,,即
∵,
∴
∴以a、b、c为三边的三角形是直角三角形,
又∵,
∴以a、b、c为三边的三角形是等腰直角三角形.
本题考查了相反数的性质,一元二次方程的根与系数关系以及利用勾股定理的逆定理判定三角形的形状,正确求得a、b、c的值是解题的关键.
22.
【解析】
通过60°直角三角形和等腰直角三角形特性建立关于CD的方程等式,再解x即可.
解:过点作于点,如图所示:
则,
设,
根据题意得:,,
是等腰直角三角形,
,
在Rt△ACD中,,
,
,
,
,
解得:,
即,
答:船到海岸线的距离是.
本题考查含30°角的直角三角形的性质及勾股定理,掌握这些是本题解题关键.
23.如图,将直角三角形分割成一个正方形和两对全等的直角三角形,直角三角形ABC中,∠ACB=90°,BC=a,AC=b,AB=c,正方形IECF中,IE=EC=CF=FI=x
(1)小明发明了求正方形边长的方法:
由题意可得BD=BE=a﹣x,AD=AF=b﹣x
因为AB=BD+AD,所以a﹣x+b﹣x=c,解得x=
(2)小亮也发现了另一种求正方形边长的方法:
利用S△ABC=S△AIB+S△AIC+S△BIC可以得到x与a、b、c的关系,请根据小亮的思路完成他的求解过程:
(3)请结合小明和小亮得到的结论验证勾股定理.
【分析】(1)根据全等三角形的性质和线段的和差即得结论;
(2)根据大三角形的面积等于三个小三角形的面积和即可求解;
(3)综合(1)和(2)的结论进行推导即可得结论.
【解答】解:(2)因为S△ABC=S△ABI+S△BIC+S△AIC
=cx+ax+bx
所以x=.
答:x与a、b、c的关系为x=.
(3)根据(1)和(2)得:
x==.
即2ab=(a+b+c)(a+b﹣c)
化简得a2+b2=c2.
24.为了积极响应国家新农村建设,遂宁市某镇政府采用了移动宣讲的形式进行宣传动员.如图,笔直公路MN的一侧点A处有一村庄,村庄A到公路MN的距离为600米,假使宣讲车P周围1000米以内能听到广播宣传,宣讲车P在公路MN上沿PN方向行驶时:
(1)请问村庄能否听到宣传,请说明理由;
(2)如果能听到,已知宣讲车的速度是200米/分钟,那么村庄总共能听到多长时间的宣传?
【分析】(1)根据村庄A到公路MN的距离为600米<1000米,于是得到结论;
(2)根据勾股定理得到BP=BQ=800米,求得PQ=1600米,于是得到结论.
【解答】解:(1)村庄能否听到宣传,
理由:∵村庄A到公路MN的距离为600米<1000米,
∴村庄能听到宣传;
(2)如图:假设当宣讲车行驶到P点开始影响村庄,行驶QD点结束对村庄的影响,
则AP=AQ=1000米,AB=600米,
∴BP=BQ=米,
∴PQ=1600米,
∴影响村庄的时间为:1600÷200=8分钟,
∴村庄总共能听到8分钟的宣传.
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每小题3分,共30分)
1.下列各组数中,能作为直角三角形三边长的是( )
A.4,5,6 B.5,7,12 C.3,5, D.1,,
2.如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,则AB的长为( )
A.2 B.3 C.2 D.2
A.10km B.12km C.13km D.26km
2题图 4题图 5题图 6题图
3.一直角三角形的斜边长比其中一直角边长大3,另一直角边长为9,则斜边长为( )
A.15 B.12 C.10 D.9
4.如图,在边长为1个单位长度的小正方形网格中,点A、B都是格点(即网格线的交点),则线段AB的长度为( )
A.3 B.5 C.6 D.4
5.如图,Rt△ABC中,∠ABC=90°,∠BAC=30°,AC=2,分别以三边为直径画半圆,则两个月形图案的面积之和(阴影部分的面积)是( )
A. B.π C. D.
6.我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边长分别为a、b,那么(a﹣b)2的值是( )
A.1 B.2 C.12 D.13
7.如图,AC=BC=BE=DE=10cm,点A、B、D在同一条直线上,AB=12cm,BD=16cm,则点C和点E之间的距离是( )
A.6cm B.7cm C.8cm D.
7题图 8题图 9题图
8.为预防新冠疫情,民生大院入口的正上方 A 处装有红外线激光测温仪(如图所示),测温仪离地面的距离 AB=2.4 米,当人体进入感应范围内时,测温仪就会自动测温并报告人体体温.当身高为 1.8 米的市民 CD 正对门缓慢走到离门 0.8 米的地方时(即 BC=0.8 米),测温仪自动显示体温,则人头顶离测温仪的距离 AD 等于( )
A.1.0 米 B.1.2 米 C.1.25 米 D.1.5 米
9.如图,圆柱的底面周长为12cm,AB是底面圆的直径,在圆柱表面的高BC上有一点D,且,.一只蚂蚁从点A出发,沿着圆柱体的表面爬行到点D的最短路程是( )cm.
A.14 B.12 C.10 D.8
10. 如图,将一个等腰直角三角形按图示方式依次翻折,若DE=a,则下列说法正确的是( )
①DC'平分∠BDE;②BC长为a+ 2a;③△BCD是等腰三角形;④ CED的周长等于BC的长.
A.①②③ B.②④ C.②③④ D.③④
二、填空题(每题3分,共24分)
11.写出命题“如果a=b,那么3a=3b”的逆命题: .
12. 已知的三边长分别是6,8,10,则的面积是__________.
13. 已知一个三角形的三边长为5,12,13,则此三角形最长边上的高=________.
14. 如图,数轴上点A所表示的实数是______.
14题图 15题图
15.如图,在Rt△ABC中,∠ACB=90°,D是△ABC内的一个动点,满足AC2﹣AD2=CD2.若AB=2,BC=4,则BD长的最小值为 .
16.如今人们锻炼身体的意识日渐增强,但是发现少数人保护环境的意识仍显淡薄,应提醒注意.如图是房山某公园的一角,有人为了抄近道而避开路的拐角∠ABC(∠ABC=90°),于是在草坪内走出了一条不该有的“捷径路AC”.已知AB=30米,BC=40米,他们踩坏了 米的草坪,只为少走 米的路.
16题图 17题图
17.甲、乙两艘客轮分别用和速度同时离开港口,甲、乙客轮分别都用到达A、B两点,若A,B两点的直线距离为,甲客轮沿着北偏东的方向航行,则乙客轮的航行方向可能是___________.(只填序号)
①北偏西 ②南偏西 ③南偏东 ④南偏西
18.如图,在中,,且周长为,点从点开始,沿边向点以每秒的速度移动;点从点开始,沿边向点以每秒的速度移动.若同时出发,则过秒时,的面积为___________.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.如图,在△ABC中,,于点D,,,.请求出△ABC的面积和CD的长.
2.湖的两岸有A,B两棵景观树,数学兴趣小组设计实验测量两棵景观树之间的距离,他们在与AB垂直的BC方向上取点C,测得米,米.
求:(1)两棵景观树之间的距离;
(2)点B到直线AC的距离.
21.已知与互为相反数,且a,b为一元二次方程的两个实数根.
(1)求c、m的值;
(2)试判断以a、b、c为三边的三角形的形状,并说明理由.
22.如图,在一笔直的海岸线上有相距的、两个观测站,站在站的正东方向上,从站测得船在北偏东的方向上,从站测得船在东北方向上,则船到海岸线的距离是多少?
23.如图,将直角三角形分割成一个正方形和两对全等的直角三角形,直角三角形ABC中,∠ACB=90°,BC=a,AC=b,AB=c,正方形IECF中,IE=EC=CF=FI=x
(1)小明发明了求正方形边长的方法:
由题意可得BD=BE=a﹣x,AD=AF=b﹣x
因为AB=BD+AD,所以a﹣x+b﹣x=c,解得x=
(2)小亮也发现了另一种求正方形边长的方法:
利用S△ABC=S△AIB+S△AIC+S△BIC可以得到x与a、b、c的关系,请根据小亮的思路完成他的求解过程:
(3)请结合小明和小亮得到的结论验证勾股定理.
24.为了积极响应国家新农村建设,遂宁市某镇政府采用了移动宣讲的形式进行宣传动员.如图,笔直公路MN的一侧点A处有一村庄,村庄A到公路MN的距离为600米,假使宣讲车P周围1000米以内能听到广播宣传,宣讲车P在公路MN上沿PN方向行驶时:
(1)请问村庄能否听到宣传,请说明理由;
(2)如果能听到,已知宣讲车的速度是200米/分钟,那么村庄总共能听到多长时间的宣传?
参考答案
一.选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 C C A B A A A A D A
二.填空题:
11.如果3a=3b,那么a=b
12.答案:7
13.答案:
14.答案:2米
15.【解答】解:取AC的中点H,连接HD,HB,
在Rt△ABC中,由勾股定理得AC,
∵AC2﹣AD2=CD2.
∴∠ADC=90°,
∵点H为AC的中点,
∴DH=CH=3,
∴BH,
∵BD≥BH﹣DH,
∴BD的最小值为5﹣3=2,
故答案为:2.
16.【解答】解:在Rt△ABC中,∵AB=30米,BC=40米,
∴AC50,30+40﹣50=20(米),
∴他们踩坏了50米的草坪,只为少走20米的路.
故答案为:50,20.
17.【解答】解:∵正方形A、B的边长分别为1和2,
∴SA=1,SB=4,
∵正方形A、B、C的边长分别为直角三角形的三边长,
∴SA+SC=SB,
∴SC=4﹣1=3.
故答案为:3.
17.③
18.18
三.解答题:
19.△ABC的面积为,CD的长为cm
20.(1)A,B两点间的 距离是40米;(2)点B到直线AC的距离是24米.
21.(1),;
(2)等腰直角三角形,理由见解析
【解析】
(1)利用互为相反数的两个数的和等于0求得a+b,c,然后利用根与系数关系即可求解;
(2)将,代入 ,解方程求得与的值,然后利用勾股定理的逆定理即可求解.
(1)
∵与互为相反数,
∴
∴
∵a,b为一元二次方程的两个实数根
∴由根与系数的关系可知,
解得,;
(2)
等腰直角三角形,理由如下:
将,代入 ,
即
解得,,即
∵,
∴
∴以a、b、c为三边的三角形是直角三角形,
又∵,
∴以a、b、c为三边的三角形是等腰直角三角形.
本题考查了相反数的性质,一元二次方程的根与系数关系以及利用勾股定理的逆定理判定三角形的形状,正确求得a、b、c的值是解题的关键.
22.
【解析】
通过60°直角三角形和等腰直角三角形特性建立关于CD的方程等式,再解x即可.
解:过点作于点,如图所示:
则,
设,
根据题意得:,,
是等腰直角三角形,
,
在Rt△ACD中,,
,
,
,
,
解得:,
即,
答:船到海岸线的距离是.
本题考查含30°角的直角三角形的性质及勾股定理,掌握这些是本题解题关键.
23.如图,将直角三角形分割成一个正方形和两对全等的直角三角形,直角三角形ABC中,∠ACB=90°,BC=a,AC=b,AB=c,正方形IECF中,IE=EC=CF=FI=x
(1)小明发明了求正方形边长的方法:
由题意可得BD=BE=a﹣x,AD=AF=b﹣x
因为AB=BD+AD,所以a﹣x+b﹣x=c,解得x=
(2)小亮也发现了另一种求正方形边长的方法:
利用S△ABC=S△AIB+S△AIC+S△BIC可以得到x与a、b、c的关系,请根据小亮的思路完成他的求解过程:
(3)请结合小明和小亮得到的结论验证勾股定理.
【分析】(1)根据全等三角形的性质和线段的和差即得结论;
(2)根据大三角形的面积等于三个小三角形的面积和即可求解;
(3)综合(1)和(2)的结论进行推导即可得结论.
【解答】解:(2)因为S△ABC=S△ABI+S△BIC+S△AIC
=cx+ax+bx
所以x=.
答:x与a、b、c的关系为x=.
(3)根据(1)和(2)得:
x==.
即2ab=(a+b+c)(a+b﹣c)
化简得a2+b2=c2.
24.为了积极响应国家新农村建设,遂宁市某镇政府采用了移动宣讲的形式进行宣传动员.如图,笔直公路MN的一侧点A处有一村庄,村庄A到公路MN的距离为600米,假使宣讲车P周围1000米以内能听到广播宣传,宣讲车P在公路MN上沿PN方向行驶时:
(1)请问村庄能否听到宣传,请说明理由;
(2)如果能听到,已知宣讲车的速度是200米/分钟,那么村庄总共能听到多长时间的宣传?
【分析】(1)根据村庄A到公路MN的距离为600米<1000米,于是得到结论;
(2)根据勾股定理得到BP=BQ=800米,求得PQ=1600米,于是得到结论.
【解答】解:(1)村庄能否听到宣传,
理由:∵村庄A到公路MN的距离为600米<1000米,
∴村庄能听到宣传;
(2)如图:假设当宣讲车行驶到P点开始影响村庄,行驶QD点结束对村庄的影响,
则AP=AQ=1000米,AB=600米,
∴BP=BQ=米,
∴PQ=1600米,
∴影响村庄的时间为:1600÷200=8分钟,
∴村庄总共能听到8分钟的宣传.
