18.1.1.2 平行四边形对角线的性质 同步练习 含答案
文档属性
| 名称 | 18.1.1.2 平行四边形对角线的性质 同步练习 含答案 |
|
|
| 格式 | docx | ||
| 文件大小 | 245.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-04 00:00:00 | ||
图片预览


文档简介
第十八章 平行四边形
18.1.1 平行四边形的性质
第2课时 平行四边形对角线的性质
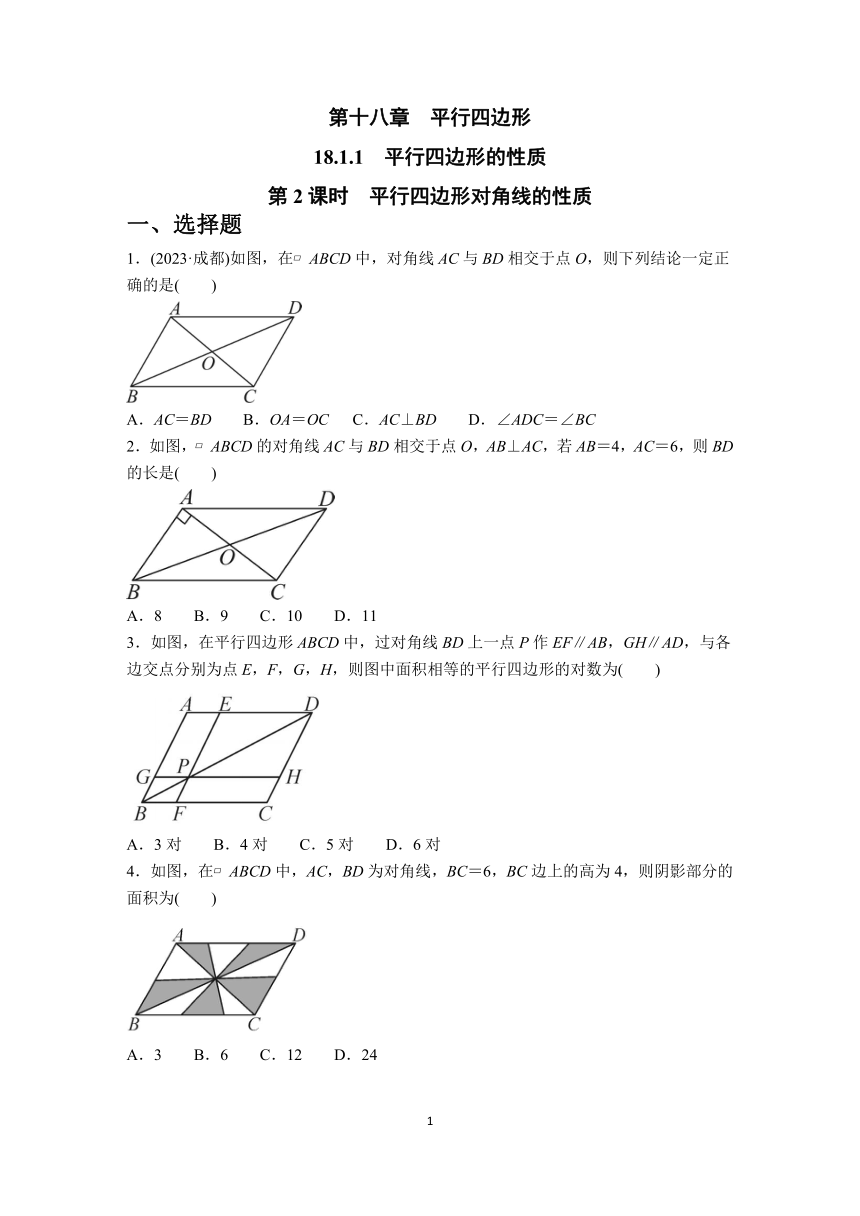
一、选择题
1.(2023·成都)如图,在 ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是( )
A.AC=BD B.OA=OC C.AC⊥BD D.∠ADC=∠BC
2.如图, ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是( )
A.8 B.9 C.10 D.11
3.如图,在平行四边形ABCD中,过对角线BD上一点P作EF∥AB,GH∥AD,与各边交点分别为点E,F,G,H,则图中面积相等的平行四边形的对数为( )
A.3对 B.4对 C.5对 D.6对
4.如图,在 ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为( )
A.3 B.6 C.12 D.24
5.如图,在平行四边形ABCD中,∠ODA=90°,AC=10 cm,BD=6 cm,则AD的长为( )
A.4 cm B.5 cm C.6 cm D.8 cm
6.如图, ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE,若 ABCD的周长为28,则△ABE的周长为( )
A.28 B.24 C.21 D.14
7.如图,在 ABCD中,EF过对角线的交点O,若AB=4,AD=3,OF=1.3,则四边形BCEF的周长为( )
A.8.3 B.9.6 C.12.6 D.13.6
二、填空题
8.若 ABCD的周长为100 cm,两条对角线相交于点O,△AOB的周长比△BOC的周长多10 cm,则AB=___________cm,BC=__________cm.
9.在 ABCD中,AB=3,BC=5,对角线AC,BD相交于点O,则OA的取值范围是_______________________.
10.如图,在 ABCD中,AB=2,AD=4,AC⊥BC,则△DBC比△ABC的周长长__________.
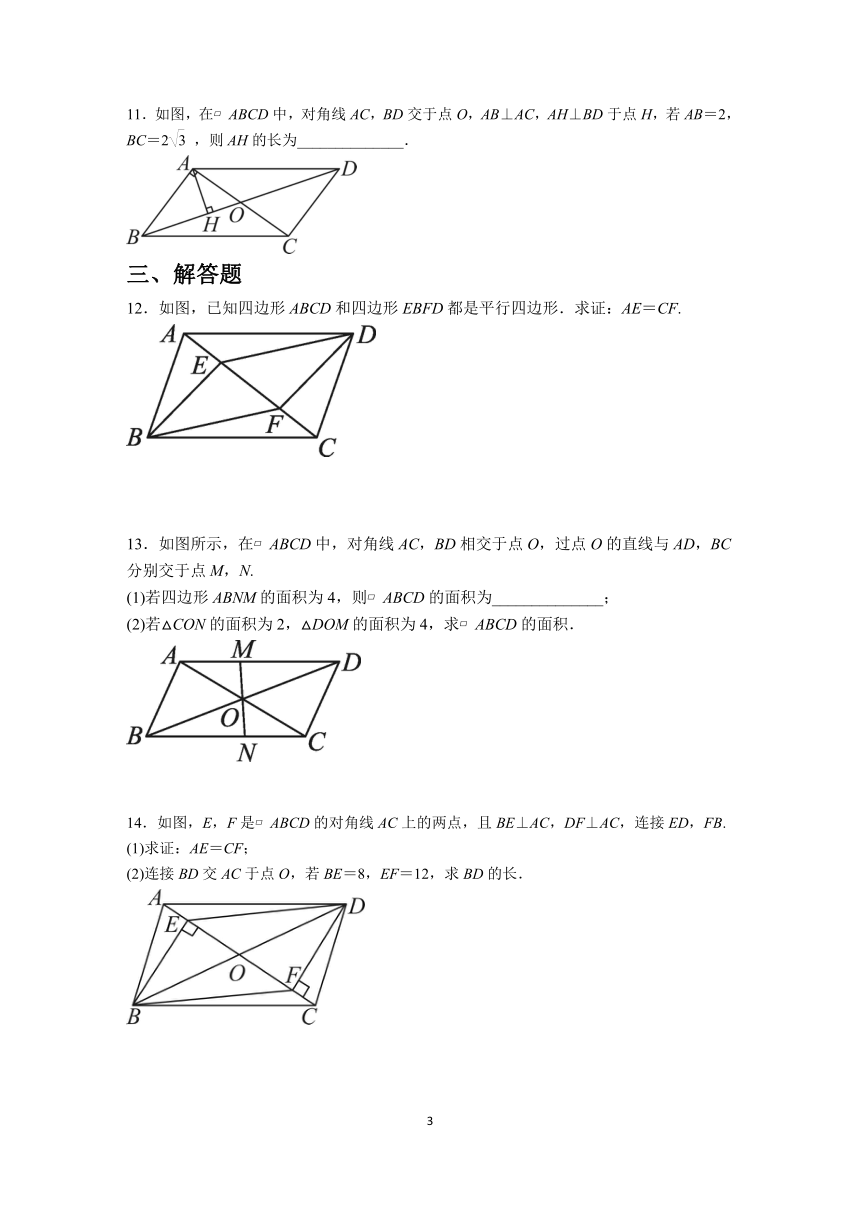
11.如图,在 ABCD中,对角线AC,BD交于点O,AB⊥AC,AH⊥BD于点H,若AB=2,BC=2,则AH的长为______________.
三、解答题
12.如图,已知四边形ABCD和四边形EBFD都是平行四边形.求证:AE=CF.
13.如图所示,在 ABCD中,对角线AC,BD相交于点O,过点O的直线与AD,BC分别交于点M,N.
(1)若四边形ABNM的面积为4,则 ABCD的面积为______________;
(2)若△CON的面积为2,△DOM的面积为4,求 ABCD的面积.
14.如图,E,F是 ABCD的对角线AC上的两点,且BE⊥AC,DF⊥AC,连接ED,FB.
(1)求证:AE=CF;
(2)连接BD交AC于点O,若BE=8,EF=12,求BD的长.
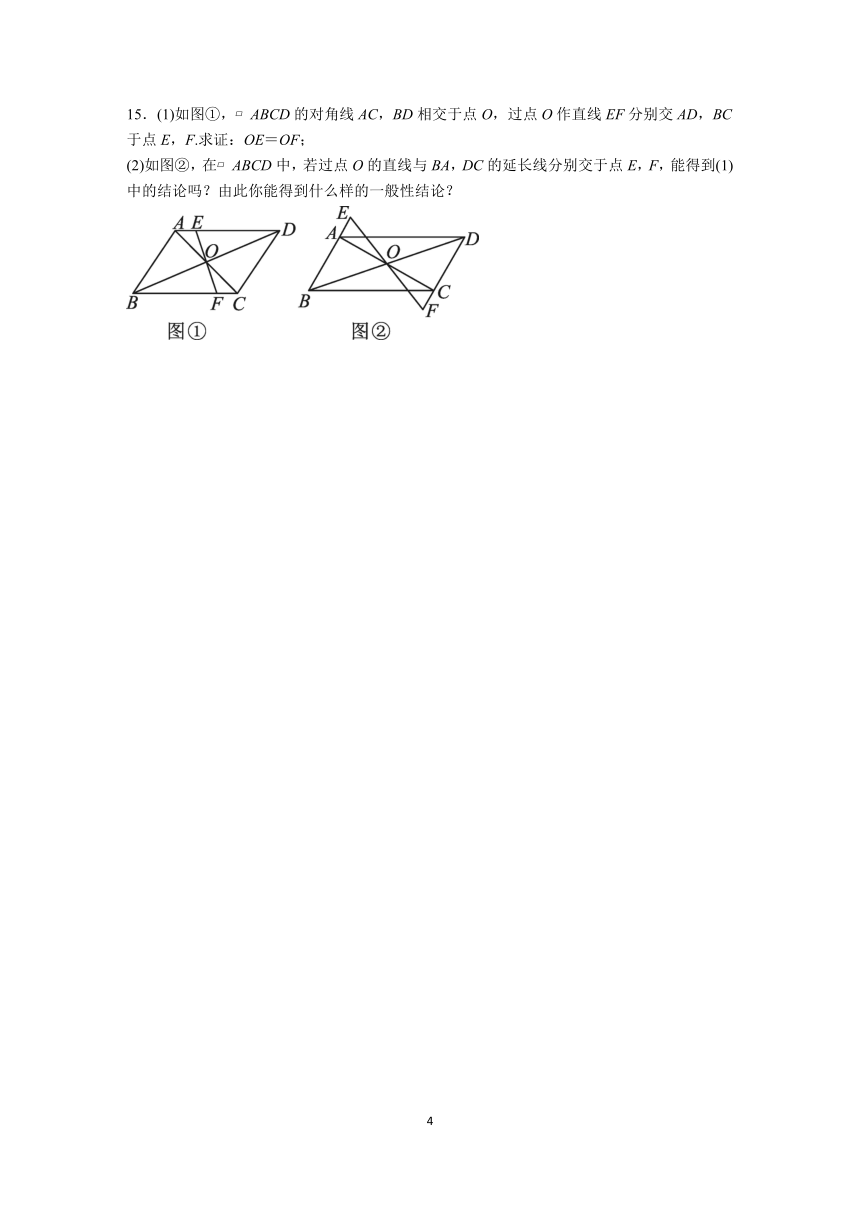
15.(1)如图①, ABCD的对角线AC,BD相交于点O,过点O作直线EF分别交AD,BC于点E,F.求证:OE=OF;
(2)如图②,在 ABCD中,若过点O的直线与BA,DC的延长线分别交于点E,F,能得到(1)中的结论吗?由此你能得到什么样的一般性结论?
1
参考答案
一、选择题
1.(2023·成都)如图,在 ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是( B )
A.AC=BD B.OA=OC C.AC⊥BD D.∠ADC=∠BC
2.如图, ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是( C )
A.8 B.9 C.10 D.11
3.如图,在平行四边形ABCD中,过对角线BD上一点P作EF∥AB,GH∥AD,与各边交点分别为点E,F,G,H,则图中面积相等的平行四边形的对数为( A )
A.3对 B.4对 C.5对 D.6对
4.如图,在 ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为( C )
A.3 B.6 C.12 D.24
5.如图,在平行四边形ABCD中,∠ODA=90°,AC=10 cm,BD=6 cm,则AD的长为( A )
A.4 cm B.5 cm C.6 cm D.8 cm
6.如图, ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE,若 ABCD的周长为28,则△ABE的周长为( D )
A.28 B.24 C.21 D.14
7.如图,在 ABCD中,EF过对角线的交点O,若AB=4,AD=3,OF=1.3,则四边形BCEF的周长为( B )
A.8.3 B.9.6 C.12.6 D.13.6
二、填空题
8.若 ABCD的周长为100 cm,两条对角线相交于点O,△AOB的周长比△BOC的周长多10 cm,则AB=___________cm,BC=__________cm.
【答案】30 30
9.在 ABCD中,AB=3,BC=5,对角线AC,BD相交于点O,则OA的取值范围是_______________________.
【答案】1<OA<4
10.如图,在 ABCD中,AB=2,AD=4,AC⊥BC,则△DBC比△ABC的周长长__________.
【答案】4
11.如图,在 ABCD中,对角线AC,BD交于点O,AB⊥AC,AH⊥BD于点H,若AB=2,BC=2,则AH的长为______________.
【答案】
三、解答题
12.如图,已知四边形ABCD和四边形EBFD都是平行四边形.求证:AE=CF.
证明:连接BD,交AC于点O,∵四边形ABCD和四边形EBFD都是平行四边形,∴OA=OC,OE=OF,∴OA-OE=OC-OF,即AE=CF
13.如图所示,在 ABCD中,对角线AC,BD相交于点O,过点O的直线与AD,BC分别交于点M,N.
(1)若四边形ABNM的面积为4,则 ABCD的面积为______________;
(2)若△CON的面积为2,△DOM的面积为4,求 ABCD的面积.
解:(1)8
(2)∵四边形ABCD是平行四边形,∴AD∥BC,OA=OC,∴∠MAC=∠NCA,又∵∠AOM=∠CON,∴△AOM≌△CON(ASA),∴S△AOM=S△CON=2,∴S△AOD=S△AOM+S△ODM=2+4=6,又∵OB=OD,∴S△AOB=S△AOD=6,∴S△ABD=S△AOB+S△AOD=6+6=12,同理可求:S△BCD=12,∴S ABCD=S△ABD+S△BCD=12+12=24
14.如图,E,F是 ABCD的对角线AC上的两点,且BE⊥AC,DF⊥AC,连接ED,FB.
(1)求证:AE=CF;
(2)连接BD交AC于点O,若BE=8,EF=12,求BD的长.
解:(1)∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴∠BAE=∠DCF,∵BE⊥AC,DF⊥AC,∴BE∥DF,∠AEB=∠CFD=90°,在△ABE和△CDF中,∴△ABE≌△CDF(AAS),∴AE=CF
(2)由△ABE≌△CDF得:BE=DF,BE∥DF,∴四边形BEDF为平行四边形,∴OB=OD,OE=OF=EF=6,∵BE⊥AC,∴∠BEO=90°,∴OB===10,∴BD=2OB=20
15.(1)如图①, ABCD的对角线AC,BD相交于点O,过点O作直线EF分别交AD,BC于点E,F.求证:OE=OF;
(2)如图②,在 ABCD中,若过点O的直线与BA,DC的延长线分别交于点E,F,能得到(1)中的结论吗?由此你能得到什么样的一般性结论?
解:(1)∵四边形ABCD为平行四边形,∴AD∥BC,OA=OC.∴∠EAO=∠FCO,∠AEO=∠CFO.∴△AEO≌△CFO(AAS).∴OE=OF
(2)能得到(1)中的结论.证明如下:∵四边形ABCD为平行四边形,∴AB∥CD,OA=OC.∴∠EAO=∠FCO,∠AEO=∠CFO.∴△AEO≌△CFO(AAS).∴OE=OF.一般性结论是:过平行四边形对角线的交点O作一条直线与平行四边形相对的两边或其延长线相交于E,F两点,则OE=OF
18.1.1 平行四边形的性质
第2课时 平行四边形对角线的性质
一、选择题
1.(2023·成都)如图,在 ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是( )
A.AC=BD B.OA=OC C.AC⊥BD D.∠ADC=∠BC
2.如图, ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是( )
A.8 B.9 C.10 D.11
3.如图,在平行四边形ABCD中,过对角线BD上一点P作EF∥AB,GH∥AD,与各边交点分别为点E,F,G,H,则图中面积相等的平行四边形的对数为( )
A.3对 B.4对 C.5对 D.6对
4.如图,在 ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为( )
A.3 B.6 C.12 D.24
5.如图,在平行四边形ABCD中,∠ODA=90°,AC=10 cm,BD=6 cm,则AD的长为( )
A.4 cm B.5 cm C.6 cm D.8 cm
6.如图, ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE,若 ABCD的周长为28,则△ABE的周长为( )
A.28 B.24 C.21 D.14
7.如图,在 ABCD中,EF过对角线的交点O,若AB=4,AD=3,OF=1.3,则四边形BCEF的周长为( )
A.8.3 B.9.6 C.12.6 D.13.6
二、填空题
8.若 ABCD的周长为100 cm,两条对角线相交于点O,△AOB的周长比△BOC的周长多10 cm,则AB=___________cm,BC=__________cm.
9.在 ABCD中,AB=3,BC=5,对角线AC,BD相交于点O,则OA的取值范围是_______________________.
10.如图,在 ABCD中,AB=2,AD=4,AC⊥BC,则△DBC比△ABC的周长长__________.
11.如图,在 ABCD中,对角线AC,BD交于点O,AB⊥AC,AH⊥BD于点H,若AB=2,BC=2,则AH的长为______________.
三、解答题
12.如图,已知四边形ABCD和四边形EBFD都是平行四边形.求证:AE=CF.
13.如图所示,在 ABCD中,对角线AC,BD相交于点O,过点O的直线与AD,BC分别交于点M,N.
(1)若四边形ABNM的面积为4,则 ABCD的面积为______________;
(2)若△CON的面积为2,△DOM的面积为4,求 ABCD的面积.
14.如图,E,F是 ABCD的对角线AC上的两点,且BE⊥AC,DF⊥AC,连接ED,FB.
(1)求证:AE=CF;
(2)连接BD交AC于点O,若BE=8,EF=12,求BD的长.
15.(1)如图①, ABCD的对角线AC,BD相交于点O,过点O作直线EF分别交AD,BC于点E,F.求证:OE=OF;
(2)如图②,在 ABCD中,若过点O的直线与BA,DC的延长线分别交于点E,F,能得到(1)中的结论吗?由此你能得到什么样的一般性结论?
1
参考答案
一、选择题
1.(2023·成都)如图,在 ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是( B )
A.AC=BD B.OA=OC C.AC⊥BD D.∠ADC=∠BC
2.如图, ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是( C )
A.8 B.9 C.10 D.11
3.如图,在平行四边形ABCD中,过对角线BD上一点P作EF∥AB,GH∥AD,与各边交点分别为点E,F,G,H,则图中面积相等的平行四边形的对数为( A )
A.3对 B.4对 C.5对 D.6对
4.如图,在 ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为( C )
A.3 B.6 C.12 D.24
5.如图,在平行四边形ABCD中,∠ODA=90°,AC=10 cm,BD=6 cm,则AD的长为( A )
A.4 cm B.5 cm C.6 cm D.8 cm
6.如图, ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE,若 ABCD的周长为28,则△ABE的周长为( D )
A.28 B.24 C.21 D.14
7.如图,在 ABCD中,EF过对角线的交点O,若AB=4,AD=3,OF=1.3,则四边形BCEF的周长为( B )
A.8.3 B.9.6 C.12.6 D.13.6
二、填空题
8.若 ABCD的周长为100 cm,两条对角线相交于点O,△AOB的周长比△BOC的周长多10 cm,则AB=___________cm,BC=__________cm.
【答案】30 30
9.在 ABCD中,AB=3,BC=5,对角线AC,BD相交于点O,则OA的取值范围是_______________________.
【答案】1<OA<4
10.如图,在 ABCD中,AB=2,AD=4,AC⊥BC,则△DBC比△ABC的周长长__________.
【答案】4
11.如图,在 ABCD中,对角线AC,BD交于点O,AB⊥AC,AH⊥BD于点H,若AB=2,BC=2,则AH的长为______________.
【答案】
三、解答题
12.如图,已知四边形ABCD和四边形EBFD都是平行四边形.求证:AE=CF.
证明:连接BD,交AC于点O,∵四边形ABCD和四边形EBFD都是平行四边形,∴OA=OC,OE=OF,∴OA-OE=OC-OF,即AE=CF
13.如图所示,在 ABCD中,对角线AC,BD相交于点O,过点O的直线与AD,BC分别交于点M,N.
(1)若四边形ABNM的面积为4,则 ABCD的面积为______________;
(2)若△CON的面积为2,△DOM的面积为4,求 ABCD的面积.
解:(1)8
(2)∵四边形ABCD是平行四边形,∴AD∥BC,OA=OC,∴∠MAC=∠NCA,又∵∠AOM=∠CON,∴△AOM≌△CON(ASA),∴S△AOM=S△CON=2,∴S△AOD=S△AOM+S△ODM=2+4=6,又∵OB=OD,∴S△AOB=S△AOD=6,∴S△ABD=S△AOB+S△AOD=6+6=12,同理可求:S△BCD=12,∴S ABCD=S△ABD+S△BCD=12+12=24
14.如图,E,F是 ABCD的对角线AC上的两点,且BE⊥AC,DF⊥AC,连接ED,FB.
(1)求证:AE=CF;
(2)连接BD交AC于点O,若BE=8,EF=12,求BD的长.
解:(1)∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴∠BAE=∠DCF,∵BE⊥AC,DF⊥AC,∴BE∥DF,∠AEB=∠CFD=90°,在△ABE和△CDF中,∴△ABE≌△CDF(AAS),∴AE=CF
(2)由△ABE≌△CDF得:BE=DF,BE∥DF,∴四边形BEDF为平行四边形,∴OB=OD,OE=OF=EF=6,∵BE⊥AC,∴∠BEO=90°,∴OB===10,∴BD=2OB=20
15.(1)如图①, ABCD的对角线AC,BD相交于点O,过点O作直线EF分别交AD,BC于点E,F.求证:OE=OF;
(2)如图②,在 ABCD中,若过点O的直线与BA,DC的延长线分别交于点E,F,能得到(1)中的结论吗?由此你能得到什么样的一般性结论?
解:(1)∵四边形ABCD为平行四边形,∴AD∥BC,OA=OC.∴∠EAO=∠FCO,∠AEO=∠CFO.∴△AEO≌△CFO(AAS).∴OE=OF
(2)能得到(1)中的结论.证明如下:∵四边形ABCD为平行四边形,∴AB∥CD,OA=OC.∴∠EAO=∠FCO,∠AEO=∠CFO.∴△AEO≌△CFO(AAS).∴OE=OF.一般性结论是:过平行四边形对角线的交点O作一条直线与平行四边形相对的两边或其延长线相交于E,F两点,则OE=OF
