高一必修一1.3函数的最值
图片预览





文档简介
课件15张PPT。1.3.1 单调性与最大(小)值 第三课时 函数的最值问题提出1.确定函数的单调性有哪些手段和方法?2.函数图象上升与下降反映了函数的单调性,
如果函数的图象存在最高点或最低点,它又
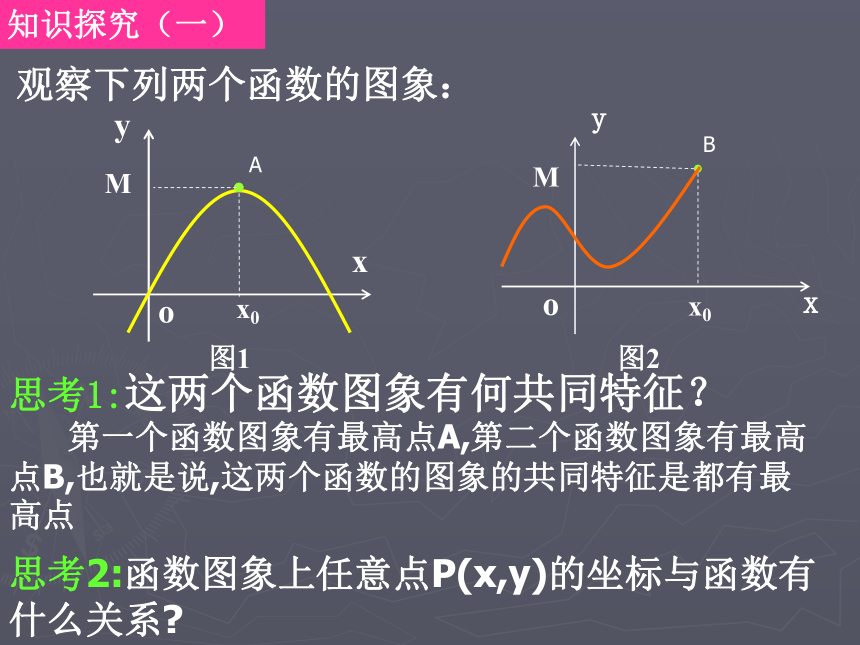
反映了函数的什么性质?函数的最值知识探究(一)观察下列两个函数的图象: 思考1:这两个函数图象有何共同特征?AB 第一个函数图象有最高点A,第二个函数图象有最高点B,也就是说,这两个函数的图象的共同特征是都有最高点思考2:函数图象上任意点P(x,y)的坐标与函数有什么关系? 函数图象上任意点P(x,y)的意义:横坐标x是自变量的取值,纵坐标y是自变量为x时对应的函数值的大小.思考3:函数图象上最高点的纵坐标叫什么名称? 函数图象上最高点的纵坐标是所有函数值中的最大值,即函数的最大值思考4:设函数y=f(x)图象上最高点的纵坐标为M,则对函数定义域内任意自变量x,f(x)与M的大小关系如何?f(x) ≤M思考5:设函数f(x)=1-x2,则f(x) ≤2成立吗?f(x)的最大值是2吗?为什么?思考6:在数学中,形如问题1中的函数y=f(x)的图象上最高点A、B的纵坐标就是函数y=f(x)的最大值,谁能给出函数最大值的定义,用什么符号表示?思考7:函数的最大值的定义中f(x) ≤M即f(x) ≤f(x0),这个不等式反映了函数y=f(x)的函数值具有什么特点?其图象又具有什么特征? f(X) ≤M反映了函数y=f(X)的所有函数值不大于实数M,这个函数的特征是图象有最高点,并且最高点的纵坐标是M。思考8:函数最大值的几何意义是什么?函数图象最高点的纵坐标。思考9:函数 有最大
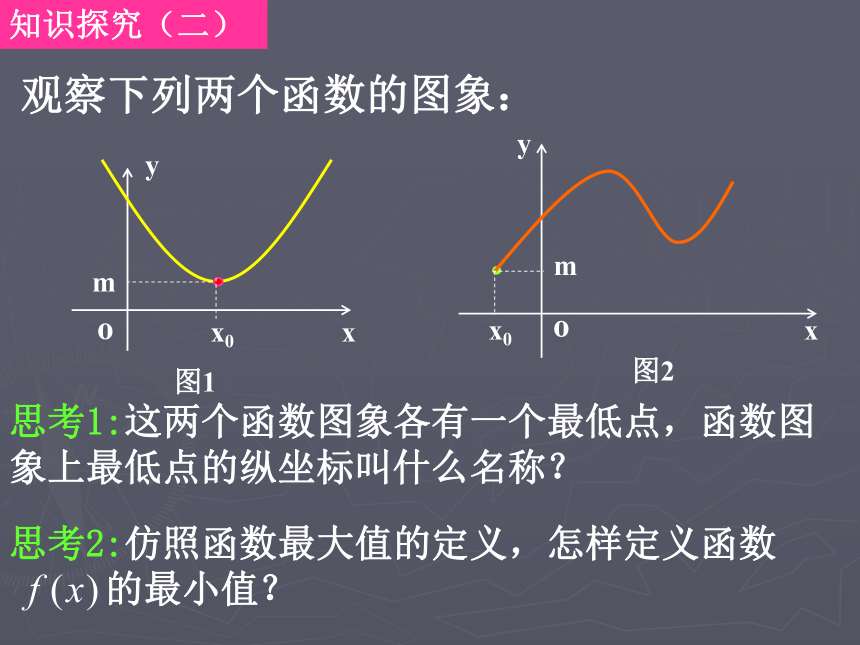
值吗?为什么?点(-1,3)是不是最高点?思考10:由问题9你发现了什么值得注意的地方?讨论函数的最大值,要坚持定义域优先的原则;函数图象有最高点时,这个函数才存在最大值,最高点必须是函数图象上的点。知识探究(二)观察下列两个函数的图象: 思考1:这两个函数图象各有一个最低点,函数图
象上最低点的纵坐标叫什么名称?思考2:仿照函数最大值的定义,怎样定义函数
的最小值? 一般地,设函数 的定义域为I,如果存在实数m满足:
(1)对于任意的 , 都有 ;
(2)存在 ,使得 .
那么称m是函数 的最小值,记作函数最小值的几何意义:函数图象最低点的纵坐标。讨论函数的最小值,要坚持定义域优先的原则;函数图象有最低点时,这个函数才存在最小值,最低点必须是函数图象上的点。知识探究(三)思考1:如果在函数 定义域内存在x1和 x2,
使对定义域内任意x都有
成立,由此你能得到什么结论?思考2:如果函数 存在最大值,那么有几个?思考3:如果函数 的最大值是b,最小值是a,
那么函数 的值域是[a,b]吗?理论迁移例1已知函数 ,求函数
的最大值和最小值. 单调法求函数最值:先判断函数的单调性,再利用其单调性求最值;常用到以下一些结论:
①如果函数y=f(X)在区间(a,b]上单调递增,在区间[b,c)上单调递减,则函数y=f(X)在x=b处有最大值f(b).
②如果函数y=f(X)在区间(a,b]上单调递减,在区间[b,c)上单调递增,则函数y=f(X)在x=b处有最小值f(b).
③如果函数y=f(X)在区间[a,b]上单调递增,则函数函数y=f(X)在x=b处有最大值f(b).在x=a处有最小值f(a).1、利用函数单调性的求函数的最大(小)值
例 2 “菊花”烟花是最壮观 的烟
花之一。制造时一般是期望在它
达到最高点时爆裂,
如果烟花 距地面的
高度h m与时间t s之间的关系为
h(t)=-4.9t2+14.7t+18 ,那么烟花冲出后什么时候是
它爆裂的最佳时刻?这时距地面的高度是多少? (精确到1m)2、利用二次函数的性质(配方法)求函数的最大(小)值解:作出函数h(t)=-4.9t2+14.7t+18 的图象,如图,显然,函数图象的顶点就是烟花上升的最高点,顶点的横坐标就是烟花爆裂的最佳时刻,纵坐标就是这时距地面的高度。由二次函数的知识,对于函数h(t)=-4.9t2 +14.7t+18 ,我们有:当 时,函数有最大值
于是,烟花冲出后1.5s是它爆裂的最佳时刻,这时距地面的高度约为29m例3.将进货单价40元的商品按50元一个售出时,能卖出500个,若此商品每个涨价1元,其销售量减少10个,为了赚到最大利润,售价应定为多少? 本题主要考察二次函数的最值问题,以及应用二次函数解决实际问题的能力,解应用题步骤是①审清题意读懂题;②实际问题转化为数学问题来解决;③归纳结论。 注意:要坚持定义域优先的原则;求二次函数的最值要借助于图象即数形结合。3、利用图象求函数的最大(小)值课堂小结:(1)函数的最大(小)值的概念
(2)求函数的最大(小)值一般方法课后作业: P39 A组T5、B组T1 ①对于熟悉的 一次函数、二次函数、反比例函数等函数可以先画出其图象,根据函数的性质来求最大(小)值 ②对于不熟悉的函数或者比较复杂的函数可以先画 出其图象,观察出其单调性,再用定义证明,然后利用单调性求出函数的最值
如果函数的图象存在最高点或最低点,它又
反映了函数的什么性质?函数的最值知识探究(一)观察下列两个函数的图象: 思考1:这两个函数图象有何共同特征?AB 第一个函数图象有最高点A,第二个函数图象有最高点B,也就是说,这两个函数的图象的共同特征是都有最高点思考2:函数图象上任意点P(x,y)的坐标与函数有什么关系? 函数图象上任意点P(x,y)的意义:横坐标x是自变量的取值,纵坐标y是自变量为x时对应的函数值的大小.思考3:函数图象上最高点的纵坐标叫什么名称? 函数图象上最高点的纵坐标是所有函数值中的最大值,即函数的最大值思考4:设函数y=f(x)图象上最高点的纵坐标为M,则对函数定义域内任意自变量x,f(x)与M的大小关系如何?f(x) ≤M思考5:设函数f(x)=1-x2,则f(x) ≤2成立吗?f(x)的最大值是2吗?为什么?思考6:在数学中,形如问题1中的函数y=f(x)的图象上最高点A、B的纵坐标就是函数y=f(x)的最大值,谁能给出函数最大值的定义,用什么符号表示?思考7:函数的最大值的定义中f(x) ≤M即f(x) ≤f(x0),这个不等式反映了函数y=f(x)的函数值具有什么特点?其图象又具有什么特征? f(X) ≤M反映了函数y=f(X)的所有函数值不大于实数M,这个函数的特征是图象有最高点,并且最高点的纵坐标是M。思考8:函数最大值的几何意义是什么?函数图象最高点的纵坐标。思考9:函数 有最大
值吗?为什么?点(-1,3)是不是最高点?思考10:由问题9你发现了什么值得注意的地方?讨论函数的最大值,要坚持定义域优先的原则;函数图象有最高点时,这个函数才存在最大值,最高点必须是函数图象上的点。知识探究(二)观察下列两个函数的图象: 思考1:这两个函数图象各有一个最低点,函数图
象上最低点的纵坐标叫什么名称?思考2:仿照函数最大值的定义,怎样定义函数
的最小值? 一般地,设函数 的定义域为I,如果存在实数m满足:
(1)对于任意的 , 都有 ;
(2)存在 ,使得 .
那么称m是函数 的最小值,记作函数最小值的几何意义:函数图象最低点的纵坐标。讨论函数的最小值,要坚持定义域优先的原则;函数图象有最低点时,这个函数才存在最小值,最低点必须是函数图象上的点。知识探究(三)思考1:如果在函数 定义域内存在x1和 x2,
使对定义域内任意x都有
成立,由此你能得到什么结论?思考2:如果函数 存在最大值,那么有几个?思考3:如果函数 的最大值是b,最小值是a,
那么函数 的值域是[a,b]吗?理论迁移例1已知函数 ,求函数
的最大值和最小值. 单调法求函数最值:先判断函数的单调性,再利用其单调性求最值;常用到以下一些结论:
①如果函数y=f(X)在区间(a,b]上单调递增,在区间[b,c)上单调递减,则函数y=f(X)在x=b处有最大值f(b).
②如果函数y=f(X)在区间(a,b]上单调递减,在区间[b,c)上单调递增,则函数y=f(X)在x=b处有最小值f(b).
③如果函数y=f(X)在区间[a,b]上单调递增,则函数函数y=f(X)在x=b处有最大值f(b).在x=a处有最小值f(a).1、利用函数单调性的求函数的最大(小)值
例 2 “菊花”烟花是最壮观 的烟
花之一。制造时一般是期望在它
达到最高点时爆裂,
如果烟花 距地面的
高度h m与时间t s之间的关系为
h(t)=-4.9t2+14.7t+18 ,那么烟花冲出后什么时候是
它爆裂的最佳时刻?这时距地面的高度是多少? (精确到1m)2、利用二次函数的性质(配方法)求函数的最大(小)值解:作出函数h(t)=-4.9t2+14.7t+18 的图象,如图,显然,函数图象的顶点就是烟花上升的最高点,顶点的横坐标就是烟花爆裂的最佳时刻,纵坐标就是这时距地面的高度。由二次函数的知识,对于函数h(t)=-4.9t2 +14.7t+18 ,我们有:当 时,函数有最大值
于是,烟花冲出后1.5s是它爆裂的最佳时刻,这时距地面的高度约为29m例3.将进货单价40元的商品按50元一个售出时,能卖出500个,若此商品每个涨价1元,其销售量减少10个,为了赚到最大利润,售价应定为多少? 本题主要考察二次函数的最值问题,以及应用二次函数解决实际问题的能力,解应用题步骤是①审清题意读懂题;②实际问题转化为数学问题来解决;③归纳结论。 注意:要坚持定义域优先的原则;求二次函数的最值要借助于图象即数形结合。3、利用图象求函数的最大(小)值课堂小结:(1)函数的最大(小)值的概念
(2)求函数的最大(小)值一般方法课后作业: P39 A组T5、B组T1 ①对于熟悉的 一次函数、二次函数、反比例函数等函数可以先画出其图象,根据函数的性质来求最大(小)值 ②对于不熟悉的函数或者比较复杂的函数可以先画 出其图象,观察出其单调性,再用定义证明,然后利用单调性求出函数的最值
