第1-3单元重难点应用题达标练习-数学五年级下册北师大版(含解析)
文档属性
| 名称 | 第1-3单元重难点应用题达标练习-数学五年级下册北师大版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 535.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-05 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第1-3单元重难点应用题达标练习-数学五年级下册北师大版
1.小红和小丽各买了一瓶同样的饮料,小红喝了升饮料,小丽喝了0.3升饮料,谁喝的饮料多些?
2.一个蛋糕,笑笑和爸爸各吃了这个蛋糕的,妈妈吃了这个蛋糕的,还剩下这个蛋糕的几分之几?
3.为保证十四运顺利进行,西安市政府要对一条公路进行翻修,第一周完成全长的,第二周比第一周完成的少,少的部分占全长的,两周一共翻修了全长的几分之几?
4.李叔叔在一块菜地里种了4种蔬菜(如图),请你分别求出油菜、茄子占这块菜地的几分之几。
5.一块菜地,它的种白菜,它的种萝卜,其余的种黄瓜,种黄瓜的部分占这块菜地的几分之几?
6.一根竹竿垂直插入水中,入水部分长米,露出水面部分长米,这根竹竿有多少米?
7.小刚在电脑上打一篇文章,第一个小时打了这篇文章的,第二个小时打了这篇文章的,两个小时一共打了这篇文章的几分之几?还剩多少没有打?
8.工作人员要给博物馆的一个展台的表面(不含底面)贴上卡纸。如图,它是由两个正方体组成的,至少需要多少平方分米的卡纸才能把这个展台的表面全部贴上?(接头处忽略不计)
9.做一个无盖的长方体玻璃鱼缸,长6分米,宽5分米,高4分米。每平方分米的玻璃单价是2.5元,做这个鱼缸至少需要多少钱的玻璃?
10.王叔叔是一个外卖骑手,他新买了一个外卖箱(如下图),准备请人给外卖箱做一个保温包,至少需要多少平方厘米的布料?
11.要做一个棱长是25厘米的正方体无盖鱼缸,至少需要多少平方厘米的玻璃?
12.爸爸想制作一种无盖的长方体玻璃鱼缸,长8分米,宽5分米,高6分米。做这个鱼缸至少需要玻璃多少平方分米?
13.观察长方体的展开图(如图),计算出这个长方体的表面积。
14.小华家的卧室长6米、宽4米、高4米,门窗总面积是10平方米。现将这个房间的四面墙涂上涂料,涂上涂料的面积是多少平方米?如果每千克涂料能涂0.5平方米的墙面,至少需要购买多少千克的涂料?
15.用涂料粉刷教室,已知教室的长、宽、高分别为9米、6米、3米。要粉刷教室的天花板和四面墙壁,扣除门窗面积40平方米,每平方米需要涂料0.5千克,粉刷这间教室至少需要多少千克的涂料?
16.一个长方体按以下方法分别割成了两个长方体,得到两个长方体的表面积之和比原来长方体的表面积分别增加了16平方厘米,24平方厘米,32平方厘米,原来长方体的表面积是多少平方厘米?
17.西瓜的主要成分是水和碳水化合物,通常情况下,水约占总质量的,碳水化合物约占总质量的。一个西瓜重5千克,这个西瓜含水多少千克?
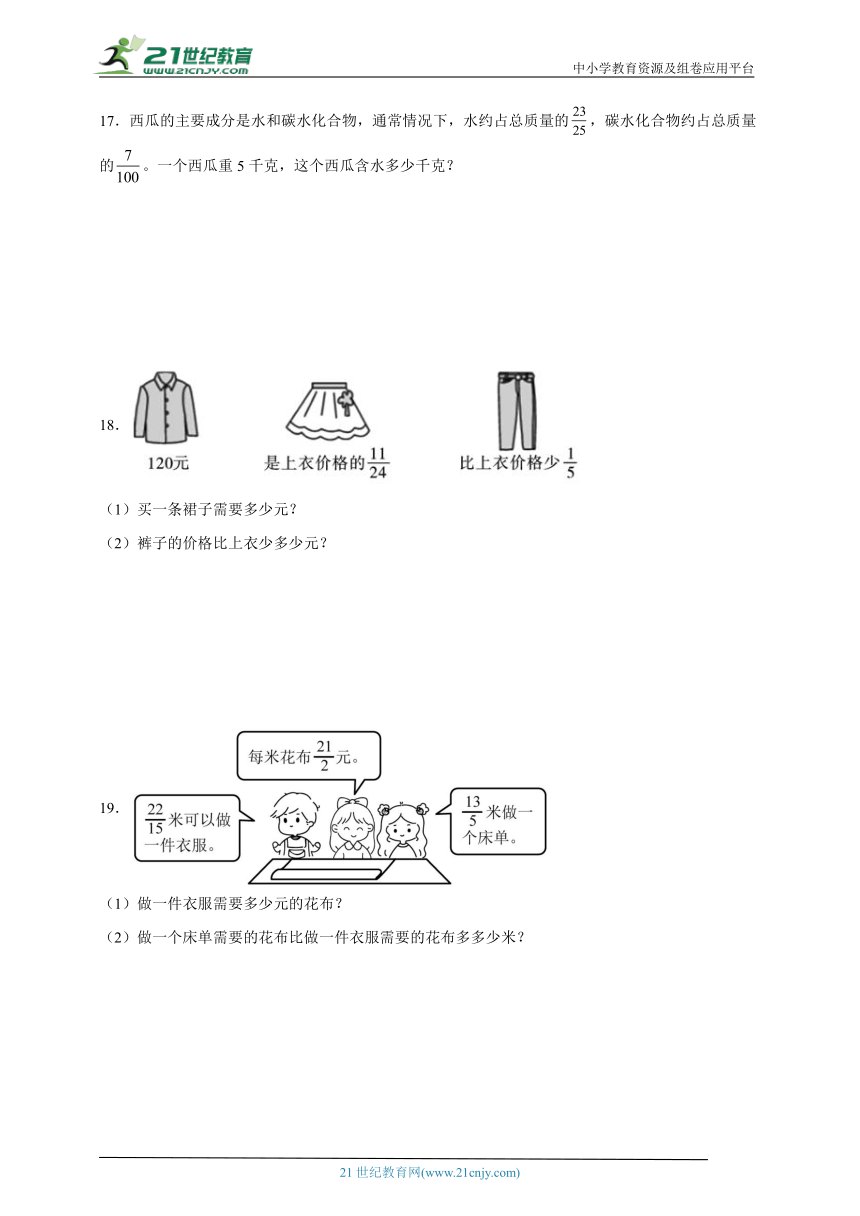
18.
(1)买一条裙子需要多少元?
(2)裤子的价格比上衣少多少元?
19.
(1)做一件衣服需要多少元的花布?
(2)做一个床单需要的花布比做一件衣服需要的花布多多少米?
20.一头骆驼的体重是440千克,它的驼峰里储存的胶质脂肪约占体重的,驼峰里储存的胶质脂肪大约有多少千克?
21.龙芯电脑公司九月份计划生产电脑6000台,实际上半月完成了计划的,下半月完成了计划的,全月实际比计划超产多少台?
22.某旅游景点去年第三季度接待的游客数量是上半年的,上半年接待的游客数量是全年的。
(1)第三季度接待的游客数量是全年的几分之几?
(2)第四季度接待的游客数量是全年的几分之几?
23.一批货物有480吨,甲车运走,乙车运走了,两车一共运走了多少吨?
24.我们学校兴趣小组共有126人,其中舞蹈组占了,唱歌组占了,美术组的人数是舞蹈组的,舞蹈组、唱歌组、美术组各有多少人?
参考答案:
1.小丽
【分析】分数和小数比较:可以将分数化为小数,再按照小数比较大小的方法进行比较;据此解答。
【详解】升=0.2升
0.2<0.3
答:小丽喝的饮料多。
【点睛】本题考查了分数和小数比较大小的方法,此题将分数化为小数比较更简便。
2.
【分析】把这个蛋糕整体看作单位“1”,用1分别减去笑笑和爸爸吃了这个蛋糕的分率,减去妈妈吃了这个蛋糕的分率,即可求出还剩下这个蛋糕的几分之几。据此解答。
【详解】1---
=--
=-
=-
=
答:还剩下这个蛋糕的。
【点睛】本题考查分数加减法的计算,关键明确要减去笑笑吃这块蛋糕的分率,减去爸爸吃了这个蛋糕的分率。
3.
【分析】把这条公路的长度看作单位“1”,用第一周修的占全长的分率,减去得出第二周修的分率,再与第一周修的占全长的分率相加,即可解答。
【详解】-+
=-+
=+
=
答:两周一共翻修了全长的。
【点睛】本题考查分数加减混合运算,关键是求出第二周修了全长的几分之几。
4.油菜;茄子
【分析】用减去黄瓜、西红柿所占的分率即可求出油菜所占分率;用1减去黄瓜、西红柿、油菜所占的分率即可求出茄子所占分率。
【详解】--=
1-=
答:油菜占这块菜地的,茄子占这块菜地的。
【点睛】这道题解题的关键是会正确进行分数加减法的计算。
5.
【分析】把这块地的总面积看作单位“1”,用单位“1”减去白菜占的分率,减去萝卜占的分率,剩下的就是黄瓜占这块地的几分之几。
【详解】1--
= - -
= -
=
=
答:种黄瓜的部分占这块地的。
【点睛】题本关键确定单位“1”,未知的占地的几分之几就用单位“1”减去已知的占地的几分之几。
6.米
【分析】根据题意可知,用入水部分的长度+露出水面部分的长度=这根竹竿的长度,据此列式解答。
【详解】(米)
答:这根竹竿有米。
【点睛】此题主要考查学生对分数加法的应用。
7. ;
【分析】把两个小时打的分率相加即可求出一共打了几分之几,用1减去一共打的分率即可求出还剩下的分率。
【详解】
答:两个小时一共打了这篇文章的,还剩没有打。
【点睛】分数加减法运算法则是本题的考查重点。
8.216平方分米
【分析】
将上面小正方体的最上面的一个面平移到下面大正方体被小正方体底面挡住的面,则大正方体的贴卡纸的面积是除了底面以外其他的5个面的面积,上面小正方体的被平移了一个正方形的面,则小正方体的表面积也就是4个面的面积。则这个展台的表面需要卡纸的面积=下面正方体的棱长×棱长×5+小正方体的棱长×棱长×4。
【详解】6×6×5+3×3×4
=180+36
=216(平方分米)
答:至少需要216平方分米的卡纸才能把这个展台的表面全部贴上。
9.295元
【分析】先搞清这道题是求长方体的表面积,其次这个长方体的表面由五个长方形组成,缺少上面,计算出这5个面的总面积;然后根据单价×数量=总价,即可求出做这个鱼缸至少需要多少钱的玻璃。
【详解】(6×5+6×4×2+5×4×2)×2.5
=(30+24×2+20×2)×2.5
=(30+48+40)×2.5
=(78+40)×2.5
=118×2.5
=295(元)
答:做这个鱼缸至少需要295元的玻璃。
【点睛】这是一道长方体表面积的实际应用,在计算时要分清需要计算几个长方形面的面积,缺少的是哪一个面的面积,从而列式解答即可。
10.10138平方厘米
【分析】
由图可知是一个长方体,根据长方体的表面积=(长×宽+长×高+宽×高)×2得出这个长方体保温包需要的布料。且由于图中的长方体是一个特殊的长方体,这个长方体有两个面是正方形,即上下和前后的四个面的面积相等的长方形,左右是面积相等的正方形,则这个长方体的表面积=长×宽×4+宽×高×2。
【详解】37×37×2+50×37×4
=2738+7400
=10138(平方厘米)
答:至少需要10138平方厘米的布料。
11.3125平方厘米
【分析】由于是无盖的,所以求正方体5个面的面积的和即可,根据正方体5个面的表面积公式:棱长×棱长×5,把数代入公式即可求解。
【详解】25×25×5
=625×5
=3125(平方厘米)
答:至少需要3125平方厘米的玻璃。
【点睛】本题主要考查正方体表面积公式,关键是看清楚需要求几个面的面积。
12.196平方分米
【分析】根据无盖长方体的表面积公式:长×宽+(长×高+宽×高)×2,把数代入公式即可求解。
【详解】8×5+(8×6+5×6)×2
=40+(48+30)×2
=40+78×2
=40+156
=196(平方分米)
答:做这个鱼缸至少需要玻璃196平方分米。
【点睛】本题主要考查无盖长方体的表面积公式,熟练掌握它的公式并灵活运用。
13.248平方厘米
【分析】通过观察长方体的展开图可知,这个长方体的长是10cm,宽是6cm,高是4cm,根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
【详解】(10×6+10×4+6×4)×2
=(60+40+24)×2
=124×2
=248(cm2)
答:这个长方体的表面积是248cm2。
【点睛】此题主要考查长方体表面积公式的灵活运用,关键是熟记公式。
14.70平方米;140千克
【分析】根据题意可知,刷涂料的部分是这个长方体的4个侧面,根据长方体的表面积公式,求出这4个侧面的面积减去门窗面积就是刷涂料的面积,然后用刷涂料的面积除以0.5就是需要购买涂料的质量。
【详解】(6×4+4×4)×2-10
=(24+16)×2-10
=40×2-10
=80-10
=70(平方米)
70÷0.5=140(千克)
答:涂上涂料的面积是70平方米,需要购买140千克的涂料。
【点睛】此题属于长方体表面积的应用,关键是弄清求那几个面的面积,缺少哪个面,根据长方体的表面积公式解答。
15.52千克
【分析】由题意可知:需要粉刷的墙壁面积是教室的表面积减去地板的面积,再减去门窗的面积;每平方米需要的涂料量已知,从而可以用乘法计算,求出总的涂料量。
【详解】[(9×6+6×3+3×9)×2-9×6-40]×0.5
=[(54+18+27)×2-54-40]×0.5
=(99×2-94)×0.5
=(198-94)×0.5
=104×0.5
=52(千克)
答:粉刷这个教室需52千克的涂料。
【点睛】此题主要考查长方体的表面积公式在实际中的应用,计算是要弄清楚需要粉刷的墙壁有哪些,方能正确求解。
16.72平方厘米
【分析】观察图形可知,把这个长方体分别与左右面平行,上下面平行,前后面平行切,每切一次就增加两个切面的面积,把增加的切面的面积相加,就是这个长方体的表面积,据此解答。
【详解】16+24+32
=40+32
=72(平方厘米)
答:原来长方体的表面积是72平方厘米。
【点睛】本题考查长方体的切割方法,关键是明确增加了哪两个切面的面积。
17.千克
【分析】由于水约占总质量的,碳水化合物约占总质量的,单位“1”是总质量,单位“1”已知,用乘法,即5×,求出水的重量。
【详解】5×=(千克)
答:这个西瓜含水千克。
【点睛】本题主要考查分数乘法的应用,求一个数的几分之几是多少,用这个数×几分之几。
18.(1)一条裙子需要55元;
(2)少24元
【分析】(1)已知上衣120元,把上衣的价格看作单位“1”,一条裙子是上衣价格的,要求这条裙子的价格,用上衣的价格×,即可解答;
(2)把上衣的价格看作单位“1”,上衣的价格×,即可得出裤子价格比上衣少多少元。
【详解】(1)(元)
答:买一条裙子需要55元。
(2)(元)
答:裤子的价格比上衣少24元。
【点睛】本题的关键是找出单位“1”,已知单位“1”的量求它的几分之几是多少用乘法。
19.(1)元
(2)米
【分析】做一件衣服、一个床单用布的米数已知,这种花布每米的价格已知,根据“总价=单价×数量”,即可求出做一件衣服需要多少元;用做床单的米数减去做衣服需要的米数,即可求得做床单比做衣服多用的米数。
【详解】(1)(元)
答:做一件衣服需要元的花布。
(2)
(米)
答:做一个床单需要的花布比做一件衣服需要的花布多米。
【点睛】此题主要是考查分数乘法的意义及应用。
20.40千克
【分析】把这头骆驼的体重看作单位“1”,根据分数乘法的意义,用骆驼的体重乘,可以计算出驼峰里储存的胶质脂肪有多少千克。
【详解】440×=40(千克)
答:驼峰里储存的胶质脂肪有40千克。
【点睛】本题考查分数乘法应用题,解题关键是先找出题目中的单位“1”是哪个量,再根据一个数乘分数的意义,列式计算。
21.900台
【分析】把计划生产的台数看成单位“1”,实际生产量计划的(+),用计划的台数乘上这个分率就是实际生产的台数,然后减去计划的台数,就是超产了多少台。
【详解】6000×(+)-6000
=6000×-6000
=6900-6000
=900(台)
答:九月份实际超产了900台。
【点睛】解答此类问题,首先找清单位“1”,进一步理清解答思路,列式的顺序,从而较好地解答问题。
22.(1)
(2)
【分析】(1)上半年接待游客数是全年的,第三季度接待的游客数量是上半年的,用上半年占全年的乘第三季度占上半年的即第三季度占全年的几分之几。
(2)把全年接待游客的总人数看成单位“1”,减去上半年及第三季度所占的几分之几即第四季度接待的游客数量是全年的几分之几。
【详解】(1)==
答:第三季度接待的游客数量是全年的。
(2)
=-
=
答:第四季度接待的游客数量是全年的。
【点睛】解答此题的关键是分清两个不同的单位“1”,已知单位“1”的量,求它的几分之几是多少用乘法求解。
23.200吨
【分析】根据题目可知,两车一共运走了这批货物的:+,由于单位“1”是这批货物,单位“1”已知,用乘法,即480×(+),算出结果即可。
【详解】480×(+)
=480×
=200(吨)
答:两车一共运走了200吨。
【点睛】本题主要考查分数乘法的应用,找准单位“1”,单位“1”已知,用乘法即可。
24.舞蹈组:36人;唱歌组:54人;美术组:18人
【分析】根据题意,用126×求出舞蹈组,用126×求出唱歌组,然后用舞蹈组人数×求出美术组。
【详解】舞蹈组:126×=36(人)
唱歌组:126×=54(人)
美术组:36×=18(人)
答:舞蹈组有36人,唱歌组有54人,美术组有18人。
【点睛】此题主要考查学生对分数乘法的实际应用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第1-3单元重难点应用题达标练习-数学五年级下册北师大版
1.小红和小丽各买了一瓶同样的饮料,小红喝了升饮料,小丽喝了0.3升饮料,谁喝的饮料多些?
2.一个蛋糕,笑笑和爸爸各吃了这个蛋糕的,妈妈吃了这个蛋糕的,还剩下这个蛋糕的几分之几?
3.为保证十四运顺利进行,西安市政府要对一条公路进行翻修,第一周完成全长的,第二周比第一周完成的少,少的部分占全长的,两周一共翻修了全长的几分之几?
4.李叔叔在一块菜地里种了4种蔬菜(如图),请你分别求出油菜、茄子占这块菜地的几分之几。
5.一块菜地,它的种白菜,它的种萝卜,其余的种黄瓜,种黄瓜的部分占这块菜地的几分之几?
6.一根竹竿垂直插入水中,入水部分长米,露出水面部分长米,这根竹竿有多少米?
7.小刚在电脑上打一篇文章,第一个小时打了这篇文章的,第二个小时打了这篇文章的,两个小时一共打了这篇文章的几分之几?还剩多少没有打?
8.工作人员要给博物馆的一个展台的表面(不含底面)贴上卡纸。如图,它是由两个正方体组成的,至少需要多少平方分米的卡纸才能把这个展台的表面全部贴上?(接头处忽略不计)
9.做一个无盖的长方体玻璃鱼缸,长6分米,宽5分米,高4分米。每平方分米的玻璃单价是2.5元,做这个鱼缸至少需要多少钱的玻璃?
10.王叔叔是一个外卖骑手,他新买了一个外卖箱(如下图),准备请人给外卖箱做一个保温包,至少需要多少平方厘米的布料?
11.要做一个棱长是25厘米的正方体无盖鱼缸,至少需要多少平方厘米的玻璃?
12.爸爸想制作一种无盖的长方体玻璃鱼缸,长8分米,宽5分米,高6分米。做这个鱼缸至少需要玻璃多少平方分米?
13.观察长方体的展开图(如图),计算出这个长方体的表面积。
14.小华家的卧室长6米、宽4米、高4米,门窗总面积是10平方米。现将这个房间的四面墙涂上涂料,涂上涂料的面积是多少平方米?如果每千克涂料能涂0.5平方米的墙面,至少需要购买多少千克的涂料?
15.用涂料粉刷教室,已知教室的长、宽、高分别为9米、6米、3米。要粉刷教室的天花板和四面墙壁,扣除门窗面积40平方米,每平方米需要涂料0.5千克,粉刷这间教室至少需要多少千克的涂料?
16.一个长方体按以下方法分别割成了两个长方体,得到两个长方体的表面积之和比原来长方体的表面积分别增加了16平方厘米,24平方厘米,32平方厘米,原来长方体的表面积是多少平方厘米?
17.西瓜的主要成分是水和碳水化合物,通常情况下,水约占总质量的,碳水化合物约占总质量的。一个西瓜重5千克,这个西瓜含水多少千克?
18.
(1)买一条裙子需要多少元?
(2)裤子的价格比上衣少多少元?
19.
(1)做一件衣服需要多少元的花布?
(2)做一个床单需要的花布比做一件衣服需要的花布多多少米?
20.一头骆驼的体重是440千克,它的驼峰里储存的胶质脂肪约占体重的,驼峰里储存的胶质脂肪大约有多少千克?
21.龙芯电脑公司九月份计划生产电脑6000台,实际上半月完成了计划的,下半月完成了计划的,全月实际比计划超产多少台?
22.某旅游景点去年第三季度接待的游客数量是上半年的,上半年接待的游客数量是全年的。
(1)第三季度接待的游客数量是全年的几分之几?
(2)第四季度接待的游客数量是全年的几分之几?
23.一批货物有480吨,甲车运走,乙车运走了,两车一共运走了多少吨?
24.我们学校兴趣小组共有126人,其中舞蹈组占了,唱歌组占了,美术组的人数是舞蹈组的,舞蹈组、唱歌组、美术组各有多少人?
参考答案:
1.小丽
【分析】分数和小数比较:可以将分数化为小数,再按照小数比较大小的方法进行比较;据此解答。
【详解】升=0.2升
0.2<0.3
答:小丽喝的饮料多。
【点睛】本题考查了分数和小数比较大小的方法,此题将分数化为小数比较更简便。
2.
【分析】把这个蛋糕整体看作单位“1”,用1分别减去笑笑和爸爸吃了这个蛋糕的分率,减去妈妈吃了这个蛋糕的分率,即可求出还剩下这个蛋糕的几分之几。据此解答。
【详解】1---
=--
=-
=-
=
答:还剩下这个蛋糕的。
【点睛】本题考查分数加减法的计算,关键明确要减去笑笑吃这块蛋糕的分率,减去爸爸吃了这个蛋糕的分率。
3.
【分析】把这条公路的长度看作单位“1”,用第一周修的占全长的分率,减去得出第二周修的分率,再与第一周修的占全长的分率相加,即可解答。
【详解】-+
=-+
=+
=
答:两周一共翻修了全长的。
【点睛】本题考查分数加减混合运算,关键是求出第二周修了全长的几分之几。
4.油菜;茄子
【分析】用减去黄瓜、西红柿所占的分率即可求出油菜所占分率;用1减去黄瓜、西红柿、油菜所占的分率即可求出茄子所占分率。
【详解】--=
1-=
答:油菜占这块菜地的,茄子占这块菜地的。
【点睛】这道题解题的关键是会正确进行分数加减法的计算。
5.
【分析】把这块地的总面积看作单位“1”,用单位“1”减去白菜占的分率,减去萝卜占的分率,剩下的就是黄瓜占这块地的几分之几。
【详解】1--
= - -
= -
=
=
答:种黄瓜的部分占这块地的。
【点睛】题本关键确定单位“1”,未知的占地的几分之几就用单位“1”减去已知的占地的几分之几。
6.米
【分析】根据题意可知,用入水部分的长度+露出水面部分的长度=这根竹竿的长度,据此列式解答。
【详解】(米)
答:这根竹竿有米。
【点睛】此题主要考查学生对分数加法的应用。
7. ;
【分析】把两个小时打的分率相加即可求出一共打了几分之几,用1减去一共打的分率即可求出还剩下的分率。
【详解】
答:两个小时一共打了这篇文章的,还剩没有打。
【点睛】分数加减法运算法则是本题的考查重点。
8.216平方分米
【分析】
将上面小正方体的最上面的一个面平移到下面大正方体被小正方体底面挡住的面,则大正方体的贴卡纸的面积是除了底面以外其他的5个面的面积,上面小正方体的被平移了一个正方形的面,则小正方体的表面积也就是4个面的面积。则这个展台的表面需要卡纸的面积=下面正方体的棱长×棱长×5+小正方体的棱长×棱长×4。
【详解】6×6×5+3×3×4
=180+36
=216(平方分米)
答:至少需要216平方分米的卡纸才能把这个展台的表面全部贴上。
9.295元
【分析】先搞清这道题是求长方体的表面积,其次这个长方体的表面由五个长方形组成,缺少上面,计算出这5个面的总面积;然后根据单价×数量=总价,即可求出做这个鱼缸至少需要多少钱的玻璃。
【详解】(6×5+6×4×2+5×4×2)×2.5
=(30+24×2+20×2)×2.5
=(30+48+40)×2.5
=(78+40)×2.5
=118×2.5
=295(元)
答:做这个鱼缸至少需要295元的玻璃。
【点睛】这是一道长方体表面积的实际应用,在计算时要分清需要计算几个长方形面的面积,缺少的是哪一个面的面积,从而列式解答即可。
10.10138平方厘米
【分析】
由图可知是一个长方体,根据长方体的表面积=(长×宽+长×高+宽×高)×2得出这个长方体保温包需要的布料。且由于图中的长方体是一个特殊的长方体,这个长方体有两个面是正方形,即上下和前后的四个面的面积相等的长方形,左右是面积相等的正方形,则这个长方体的表面积=长×宽×4+宽×高×2。
【详解】37×37×2+50×37×4
=2738+7400
=10138(平方厘米)
答:至少需要10138平方厘米的布料。
11.3125平方厘米
【分析】由于是无盖的,所以求正方体5个面的面积的和即可,根据正方体5个面的表面积公式:棱长×棱长×5,把数代入公式即可求解。
【详解】25×25×5
=625×5
=3125(平方厘米)
答:至少需要3125平方厘米的玻璃。
【点睛】本题主要考查正方体表面积公式,关键是看清楚需要求几个面的面积。
12.196平方分米
【分析】根据无盖长方体的表面积公式:长×宽+(长×高+宽×高)×2,把数代入公式即可求解。
【详解】8×5+(8×6+5×6)×2
=40+(48+30)×2
=40+78×2
=40+156
=196(平方分米)
答:做这个鱼缸至少需要玻璃196平方分米。
【点睛】本题主要考查无盖长方体的表面积公式,熟练掌握它的公式并灵活运用。
13.248平方厘米
【分析】通过观察长方体的展开图可知,这个长方体的长是10cm,宽是6cm,高是4cm,根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
【详解】(10×6+10×4+6×4)×2
=(60+40+24)×2
=124×2
=248(cm2)
答:这个长方体的表面积是248cm2。
【点睛】此题主要考查长方体表面积公式的灵活运用,关键是熟记公式。
14.70平方米;140千克
【分析】根据题意可知,刷涂料的部分是这个长方体的4个侧面,根据长方体的表面积公式,求出这4个侧面的面积减去门窗面积就是刷涂料的面积,然后用刷涂料的面积除以0.5就是需要购买涂料的质量。
【详解】(6×4+4×4)×2-10
=(24+16)×2-10
=40×2-10
=80-10
=70(平方米)
70÷0.5=140(千克)
答:涂上涂料的面积是70平方米,需要购买140千克的涂料。
【点睛】此题属于长方体表面积的应用,关键是弄清求那几个面的面积,缺少哪个面,根据长方体的表面积公式解答。
15.52千克
【分析】由题意可知:需要粉刷的墙壁面积是教室的表面积减去地板的面积,再减去门窗的面积;每平方米需要的涂料量已知,从而可以用乘法计算,求出总的涂料量。
【详解】[(9×6+6×3+3×9)×2-9×6-40]×0.5
=[(54+18+27)×2-54-40]×0.5
=(99×2-94)×0.5
=(198-94)×0.5
=104×0.5
=52(千克)
答:粉刷这个教室需52千克的涂料。
【点睛】此题主要考查长方体的表面积公式在实际中的应用,计算是要弄清楚需要粉刷的墙壁有哪些,方能正确求解。
16.72平方厘米
【分析】观察图形可知,把这个长方体分别与左右面平行,上下面平行,前后面平行切,每切一次就增加两个切面的面积,把增加的切面的面积相加,就是这个长方体的表面积,据此解答。
【详解】16+24+32
=40+32
=72(平方厘米)
答:原来长方体的表面积是72平方厘米。
【点睛】本题考查长方体的切割方法,关键是明确增加了哪两个切面的面积。
17.千克
【分析】由于水约占总质量的,碳水化合物约占总质量的,单位“1”是总质量,单位“1”已知,用乘法,即5×,求出水的重量。
【详解】5×=(千克)
答:这个西瓜含水千克。
【点睛】本题主要考查分数乘法的应用,求一个数的几分之几是多少,用这个数×几分之几。
18.(1)一条裙子需要55元;
(2)少24元
【分析】(1)已知上衣120元,把上衣的价格看作单位“1”,一条裙子是上衣价格的,要求这条裙子的价格,用上衣的价格×,即可解答;
(2)把上衣的价格看作单位“1”,上衣的价格×,即可得出裤子价格比上衣少多少元。
【详解】(1)(元)
答:买一条裙子需要55元。
(2)(元)
答:裤子的价格比上衣少24元。
【点睛】本题的关键是找出单位“1”,已知单位“1”的量求它的几分之几是多少用乘法。
19.(1)元
(2)米
【分析】做一件衣服、一个床单用布的米数已知,这种花布每米的价格已知,根据“总价=单价×数量”,即可求出做一件衣服需要多少元;用做床单的米数减去做衣服需要的米数,即可求得做床单比做衣服多用的米数。
【详解】(1)(元)
答:做一件衣服需要元的花布。
(2)
(米)
答:做一个床单需要的花布比做一件衣服需要的花布多米。
【点睛】此题主要是考查分数乘法的意义及应用。
20.40千克
【分析】把这头骆驼的体重看作单位“1”,根据分数乘法的意义,用骆驼的体重乘,可以计算出驼峰里储存的胶质脂肪有多少千克。
【详解】440×=40(千克)
答:驼峰里储存的胶质脂肪有40千克。
【点睛】本题考查分数乘法应用题,解题关键是先找出题目中的单位“1”是哪个量,再根据一个数乘分数的意义,列式计算。
21.900台
【分析】把计划生产的台数看成单位“1”,实际生产量计划的(+),用计划的台数乘上这个分率就是实际生产的台数,然后减去计划的台数,就是超产了多少台。
【详解】6000×(+)-6000
=6000×-6000
=6900-6000
=900(台)
答:九月份实际超产了900台。
【点睛】解答此类问题,首先找清单位“1”,进一步理清解答思路,列式的顺序,从而较好地解答问题。
22.(1)
(2)
【分析】(1)上半年接待游客数是全年的,第三季度接待的游客数量是上半年的,用上半年占全年的乘第三季度占上半年的即第三季度占全年的几分之几。
(2)把全年接待游客的总人数看成单位“1”,减去上半年及第三季度所占的几分之几即第四季度接待的游客数量是全年的几分之几。
【详解】(1)==
答:第三季度接待的游客数量是全年的。
(2)
=-
=
答:第四季度接待的游客数量是全年的。
【点睛】解答此题的关键是分清两个不同的单位“1”,已知单位“1”的量,求它的几分之几是多少用乘法求解。
23.200吨
【分析】根据题目可知,两车一共运走了这批货物的:+,由于单位“1”是这批货物,单位“1”已知,用乘法,即480×(+),算出结果即可。
【详解】480×(+)
=480×
=200(吨)
答:两车一共运走了200吨。
【点睛】本题主要考查分数乘法的应用,找准单位“1”,单位“1”已知,用乘法即可。
24.舞蹈组:36人;唱歌组:54人;美术组:18人
【分析】根据题意,用126×求出舞蹈组,用126×求出唱歌组,然后用舞蹈组人数×求出美术组。
【详解】舞蹈组:126×=36(人)
唱歌组:126×=54(人)
美术组:36×=18(人)
答:舞蹈组有36人,唱歌组有54人,美术组有18人。
【点睛】此题主要考查学生对分数乘法的实际应用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
