第1-3单元重难点应用题达标练习-数学五年级下册苏教版(含答案)
文档属性
| 名称 | 第1-3单元重难点应用题达标练习-数学五年级下册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 588.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-05 16:23:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第1-3单元重难点应用题达标练习-数学五年级下册苏教版
1.学校买来一批篮球和足球,篮球的个数是足球的5倍,篮球的个数比足球多32个。学校买来篮球和足球各多少个?
2.电冰箱厂今年计划生产冰箱72万台,比去年产量的2倍少6万台。去年生产冰箱多少万台?(列方程并解答)
3.学校图书馆有故事书、科技书和美术书共410本,科技书比故事书少28本,美术书比故事书少69本。三种书各有多少本?(先将下面的线段图补充完整,再解答)
4.小冬原来有一些邮票,今年又收集了35枚,送给小明40枚后,还剩50枚。小冬原来有邮票多少枚?(列方程解答)
5.学校图书馆购进文艺书和科技书共320本,其中文艺书的本数是科技书的4倍,文艺书、科技书各有多少本?(用方程解)
6.甲、乙两艘轮船同时从上海出发开往青岛。经过8小时后,乙船落后甲船24千米。乙船每小时行32.5千米,甲船每小时行多少千米?(用方程法解)
7.成渝高速路长330千米,一辆大客车从重庆开往成都,一辆小轿车同时从成都开往重庆,2小时在途中相遇,已知小轿车的速度是大客车的1.2倍,两车每小时各行多少千米?(用方程解)
8.柏树和松树一共有7500棵。柏树的棵数是松树的1.5倍。两种树各有多少棵?(列方程解答)
9.王方和李亮共收集了128枚邮票。王方送给李亮16枚后两人数量相等。王方原来有邮票多少枚?
10.“夏至”是一年中白昼最长,黑夜最短的一天。这天苏州白昼的时间大约是黑夜的1.4倍,那么这天苏州的白昼时间大约是多少小时?(用方程解)
11.学校一共有120个足球,四年级有4个班,每班借了12个,剩下的借给了五年级的4个班,五年级平均每个班借了多少个?(列方程解答)
12.下表是求知书店和育人书店2017年上半年销售教育类图书的统计表。
(1)请根据上表中的数据完成下面的折线统计图。
(2)求知书店和育人书店分别是哪个月销售图书最多?哪个月两个书店销售图书相差最大?
13.新时代商场2020年下半年空调和冰箱的销售情况如表所示:
7月份 8月份 9月份 10月份 11月份 12月份
空调 450 750 600 350 200 620
冰箱 300 550 450 350 250 200
(1)根据表中数据完成折线统计图。
(2)商场下半年平均每月销售冰箱多少台?
(3)如果每台空调的利润是150元,那么这个商场2020年第三季度空调共获利多少万元?
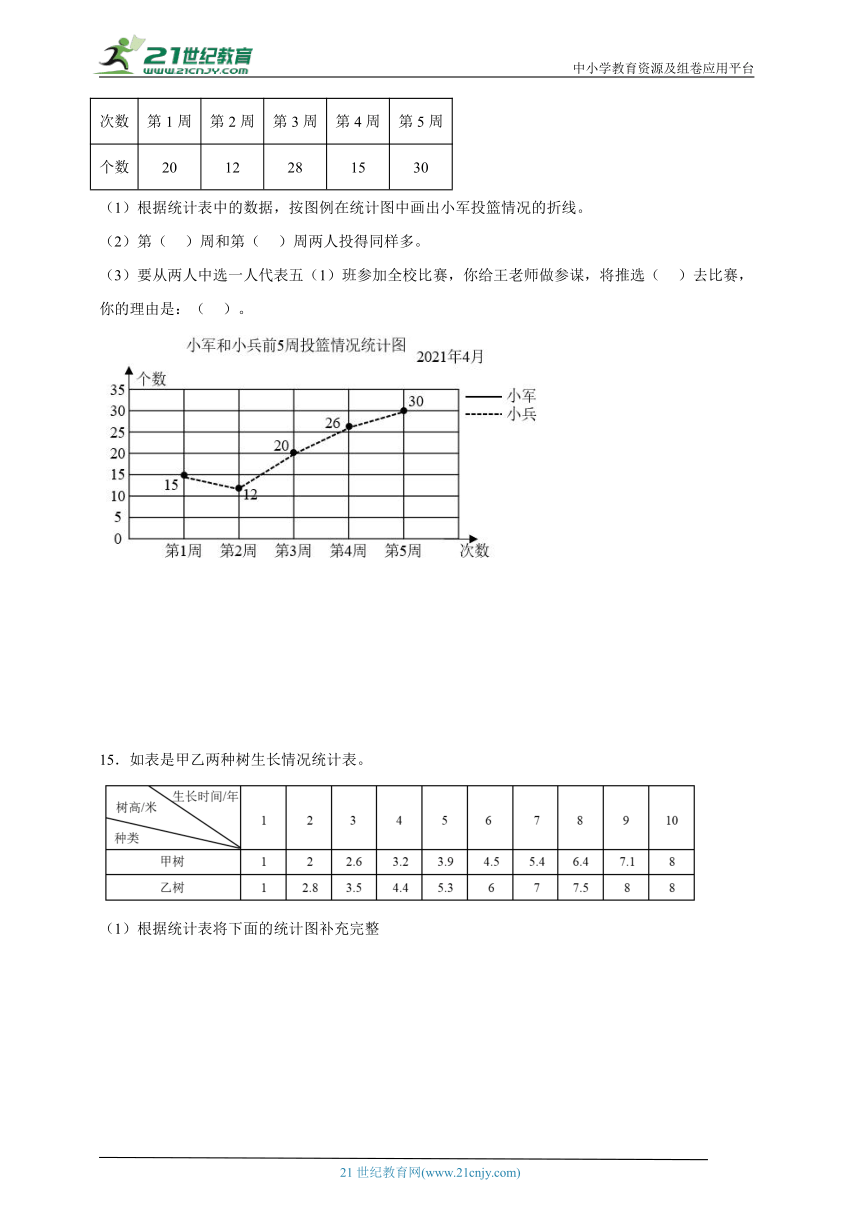
14.下一星期就要举行全校投篮比赛,每班将推出一名最优选手参赛。五(1)班公认投篮最好两位选手分别小军和小兵,派谁去呢?班主任王老师找出前5周两人进行测试的结果,以统计表和统计图形式呈现,成绩如下:
小军前5周投篮情况统计表:
次数 第1周 第2周 第3周 第4周 第5周
个数 20 12 28 15 30
(1)根据统计表中的数据,按图例在统计图中画出小军投篮情况的折线。
(2)第( )周和第( )周两人投得同样多。
(3)要从两人中选一人代表五(1)班参加全校比赛,你给王老师做参谋,将推选( )去比赛,你的理由是:( )。
15.如表是甲乙两种树生长情况统计表。
(1)根据统计表将下面的统计图补充完整
(2)从开始植树到第七年,生长速度较快的是( )。(填“甲树”或“乙树”)
(3)生长到第( )年,两棵树的高度都是8米。
16.如图是甲、乙两市2018年月平均气温变化情况。
(1)两个城市,( )市可能是南方城市。
(2)乙市( )月平均气温最低,甲市( )月平均气温最高?
(3)有一种植物的生长期为5个月,最适宜的生长温度为这种植物适合在( )市生长。(填“甲”或“乙”)
(4)从统计图中你还得到哪些信息?
17.下面是大同市2021年4月1日~7日气温统计表。(单位:℃)
(1)请你根据表中的数据,完成下面折线统计图。
(2)在4月1日~7日中,( )日气温最低,( )日气温最高。
(3)在4月1日~7日中,温差最大的是( )日,( )日和( )的温差一样。
(4)在4月1日~7日相邻的两天中,从( )日到( )日温度下降最快。
18.把一根长28分米的彩带和一根长35分米的彩带截成同样长的短彩带且没有剩余。
(1)截成的短彩带最长是多少分米?
(2)一共可以截成多少段这样的短彩带?
19.幼儿园小班的小朋友排队做操,10人一排或6人一排都恰好分完。
(1)小朋友至少有多少人?
(2)至少再增加多少人,才能排成正方形的队伍?
20.把下面的方格图(每小格边长看成1厘米)分割成几个面积最大并相等的正方形,且没有剩余。能分成多少个这样的正方形?先写出计算过程,再在图中画出分割过程。
21.姜堰城区至海险城区公交车,901路每8分钟发一辆车,路每20分钟发一辆车,这两路车第一次同时发车时间是早上,第二次同时发车是什么时候?(先列表,再回答)
901路
路
22.新区学校为美化校园,在中心路的一侧放鲜花,共放了46盆,每两盆之间的距离是2米,现在要改成每两盆之间距离是3米,有多少盆花不需要移动?
23.小明和小华两人定期到张奶奶家去打扫卫生。小明每6天去一次,小华每9天去一次。4月25日两人在张奶奶家相遇,几月几日他们又再次相遇?
参考答案:
1.足球有10个;篮球有40个
【分析】根据篮球的个数比足球多32个,可以提炼这道题的等量关系是:篮球的个数-足球的个数=32个,根据这个等量关系,列方程解答。
【详解】解:设足球有x个,篮球有5x个
5x-x=32
4x=32
4x÷4=32÷4
x=8
8×5=40(个)
答:足球有10个,篮球有40个。
【点睛】本题解题关键是找出题目中的等量关系:篮球的个数-足球的个数=32个,列方程解答。
2.39万台
【分析】设去年生产冰箱x万台,今年比去年产量的2倍少6万台,去年生产冰箱的台数×2-6=今年冰箱的台数,列方程:2x-6=72,解方程,即可解答。
【详解】解:设去年生产冰箱x万台。
2x-6=72
2x-6+6=72+6
2x=78
2x÷2=78÷2
x=39
答:去年生产冰箱39万台。
【点睛】本题主要考查运用方程解决问题的能力,解决此类问题一般方法是:根据等量关系列方程,求解。
3.图见解析;故事书:169本;科技书:141本,美术书:100本
【分析】以故事书为标准,画出一条线段,根据科技书比故事书少28本,美术书比故事书少69本,画出科技书和故事书的量是多少即可;
设故事书有x本,科技书比故事书少28本,则科技书有x-28本;美术书比故事书少69本,则美术书有x-69本,故事书、科技书和美术书共410本,即故事书的本数+科技书的本数+美术书的本数=410本,列方程:x+(x-28)+(x-69)=410,解方程,即可解答。
【详解】如图:
;
解:设故事书有x本,则科技书有x-28本,美术书有x-69本。
x+(x-28)+(x-69)=410
x+x-28+x-69=410
3x=410+28+69
3x=438+69
3x=507
x=507÷3
x=169
科技书:169-28=141(本)
美术书:169-69=100(本)
答:故事书有169本,科技书有141本,美术书有100本。
【点睛】本题考查方程的实际应用,根据三种书的数量关系,设出未知数,找出相关的量。列方程,解方程。
4.
55枚
【分析】设小冬原来有邮票x枚,根据题意:原来的邮票+35-40=50,据此列方程求解。
【详解】解:设小冬原来有邮票x枚。
x+35-40=50
x=50+40-35
x=90-35
x=55
答:小冬原来有邮票55枚。
【点睛】解答本题的关键是认真读题,找准关系式,即:原来的邮票+35-40=50。
5.文艺书:256本;科技数64本
【分析】设科技书有x本,则文艺书有4x本;根据文艺书和科技书共320本列出方程求出科技书的本数,进而得出文艺书的本数;据此解答。
【详解】解:设科技书有x本,则文艺书有4x本。
x+4x=320
5x=320
5x÷5=320÷5
x=64
4x=4×64=256
答:文艺书有256本,科技数有64本。
【点睛】本题主要考查列方程解含有两个未知数的问题,找出等量关系式是解题的关键。
6.35.5千米
【分析】设甲船每小时行x千米,根据“速度差×时间=路程差”列出方程求解即可。
【详解】解:设甲船每小时行x千米
(x-32.5)×8=24
(x-32.5)×8÷8=24÷8
x-32.5=3
x-32.5+32.5=3+32.5
x=35.5
答:甲船每小时行35.5千米。
【点睛】本题主要考查应用方程解简单的行程问题,明确“速度差×时间=路程差”是解题的关键。
7.大客车:75千米;小轿车:90千米
【分析】根据题意,小轿车的速度是大客车的1.2倍,即大客车的速度×1.2=小轿车的速度;设大客车每小时行x千米,则小轿车每小时行1.2x千米;大客车2小时行驶2x千米;小轿车2小时行驶1.2x×2千米,两车行驶的路程和等于成渝高速路的长度,列方程:2x+1.2x×2=330,解方程,即可解答。
【详解】解:设大客车每小时行x千米,则小轿车每小时1.2x千米。
2x+1.2x×2=330
2x+2.4x=330
4.4x=330
x=330÷4.4
x=75
小轿车:75×1.2=90(千米)
答:大客车每小时行75千米,小轿车每小时行90千米。
【点睛】本题考查方程的实际应用,根据大客车每小时行驶的路程和小轿车每小时行驶的路程,设出未知数,找出相关的量,列方程,解方程。
8.松树:3000棵;柏树:4500棵。
【分析】设松树有x棵,柏树的棵数是松树的1.5倍,则柏树有1.5x棵;柏树和松树一共有7500棵,即柏树棵数+松树棵数=7500,列方程:1.5x+x=7500,解方程,即可解答。
【详解】解:设松树有x棵,则柏树有1.5x棵。
1.5x+x=7500
2.5x=7500
x÷2.5=7500÷2.5
x=3000
3000×1.5=4500(棵)
答:松树有3000棵,柏树有4500棵。
【点睛】本题考查方程的实际应用,根据松树棵数和柏树棵数之间的关系,设出未知数,找出相关的量,列方程,解方程。
9.80枚
【分析】假设王方原来有邮票x枚,则李亮有(128-x)枚邮票,根据数量关系:王方邮票的数量-16=李亮邮票的数量+16,代入列出方程,解方程即可求出王方原来有多少枚邮票。
【详解】解:设王方原来有邮票x枚,则李亮有(128-x)枚邮票,
x-16=128-x+16
x+x=128+16+16
2x=160
x=80
答:王方原来有邮票80枚。
【点睛】此题的解题关键是弄清题意,把王方原来的邮票数设为未知数x,找出题中数量间的相等关系,列出包含x的等式,解方程得到最终的结果。
10.14小时
【分析】设这天苏州的黑夜时间大约是x小时,则白昼时间大约是1.4x小时,根据白昼时间+黑夜时间=24小时,列方程求解即可。
【详解】解:设这天苏州的黑夜时间大约是x小时。
1.4x+x=24
2.4x=24
x=10
1.4×10=14(小时)
答:这天苏州的白昼时间大约是14小时。
【点睛】本题主要考查列方程解含有两个未知数的问题,找出等量关系式是解题的关键。
11.18个
【分析】根据题干,设五年级平均每班借x个,则根据等量关系:四年级每班借的个数×班级数+五年级平均每班借的个数×班级数=学校足球的总个数,据此列出方程即可解决问题。
【详解】解:设五年级平均每班借x个。
12×4+4x=120
48+4x=120
48+4x-48=120-48
4x=72
4x÷4=72÷4
x=18
答:五年级平均每班借了18个。
【点睛】解答此题关键是找出数量之间的相等关系,由此列方程解答即可。
12.(1)见详解;
(2)求知书店4月份;育人书店3月份;6月份相差最大
【分析】(1)根据表中数据描点连线即可完成折线统计图;
(2)观察折线统计图,实线表示求知书店,虚线表示育人书店,找出折线最高点,此时对应的月份就是销售图书最多的月份;找出实线虚线相差最大的处,此时对应的月份就是销售图书相差最大的月份。
【详解】(1)折线统计图如下:
(2)观察折线统计图可知:求知书店4月份销售图书最多;育人书店3月份销售图书最多;6月份两个书店销售图书相差最大。
【点睛】本题主要考查统计图表的综合应用,根据表中数据画出统计图是解题的关键。
13.(1)见详解。
(2)台
(3)27万元
【分析】(1)根据统计表所提供的数据,在统计图中描出空调和冰箱销售量的点,顺次连接,标上数据等即可完成折线统计图;
(2)首先求出2020年下半年一共销售冰箱多少台;然后用它除以6,求出平均每月销售冰箱多少台即可;
(3)首先求出2020年第三季度一共销售空调多少台;然后用它乘每台冰箱获利的钱数即可。
【详解】(1)画图如下:
(2)(300+550+450+350+250+200)÷6
=2100÷6
=350(台)
答:商场下半年平均每月销售冰箱350台。
(3)(450+750+600)×150
=1800×150
=270000(元)
270000元=27万元
答:这个商场2020年第三季度空调共获利27万元。
【点睛】此题主要考查的了如何根据统计表所提供的数据绘制折线统计图、观察折线统计图,从图中获取信息,并利用获取的信息解题的能力。
14.(1)见详解
(2)2,5
(3)小兵,他的发挥比小军稳定
【分析】(1)按照小军前5周的投篮个数数描出各点,再用线段依次连接,最后在点上标出数据。
(2)观察统计图可知,第2周两人都踢了12个,第5周两人都投了30个,据此解答。
(3)表示小军投篮个数的曲线起伏较大,说明小军发挥不稳定;小兵的投篮个数程上升趋势,发挥稳定。据此解答。
【详解】(1)
(2)第2周和第5周两人投得同样多。
(3)要从两人中选一人代表五(1)班参加全校比赛,将推选小兵去比赛,你的理由是:他的发挥比小军稳定。
【点睛】本题考查复式折线统计图的应用。观察统计图,找出需要的信息是解题的关键。
15.(1)见详解
(2)乙树
(3)10
【分析】(1)根据统计表提供的数据,完成统计图;
(2)观察统计图第七年后,哪种树生长的快;
(3)观察统计图,找出第几年两棵树的高度都是8米。
【详解】(1)
(2)从开始植树到第七年,生产速度较快的是乙树;
(3)生长到第10年,两个数的高度都是8米。
【点睛】本题考查折线统计图的填充。关键是利用所给数据完成统计图并回答问题。
16.(1)甲
(2)1;8
(3)甲
(4)甲市1月平均气温比乙市高15度。
【分析】(1)甲市平均气温较高,乙市平均气温偏低,根据我国南方城市气温高北方城市气温低的特点判断;
(2)乙市1月气温数据在最低点。甲市8月数据在最高点;
(3)乙市平均气温最高25度,相比甲市5-10月气温更适合这种植物生长;
(4)统计图中能得到很多信息:如甲市1月平均气温比乙市高15度。
【详解】(1)根据我国气温南高北低的特点,甲市可能是南方城市。
(2)乙市1月份数据最小,甲市8月数据最大。
乙市1月平均气温最低,甲市8月平均气温最高。
(3)甲市5-10月平均气温在25度-32.5度之间,乙市平均气温最高在25度,这种植物适合甲市生长。
(4)从统计图中还得到很多信息。如甲市1月平均气温比乙市高15度。(答案不唯一)
【点睛】本题为复式折线统计图,分析统计图中数据,根据统计图的数据解决问题。
17.(1)见详解。
(2)3;1
(3)2;3;4
(4)2;3
【分析】(1)制作折线统计图时,先从列中找到项目,再从行中找到对应的数量高度点个点,然后顺次连点成线,复式图虚实线分开表示。
(2)比较在4月1日~7日中各天的最高和最低气温,作判断。
(3)比较在4月1日~7日中每天的温差,作判断。
(4)比较4月1日~7日相邻的两天中气温下降最大的,作判断。
【详解】(1)如图:
(2)在4月1日~7日中,3日气温最低,1日气温最高。
(3)15-2=13℃
13-(﹣2)=15℃
7-(﹣3)=10℃
12-2=10℃
14-0=14℃
11-3=8℃
13-1=12℃
答:在4月1日~7日中,温差最大的是2日,3日和4的温差一样。
(4)在4月1日~7日相邻的两天中,从2日到3日温度下降最快。
【点睛】本题考查了学生动手操作能力及从统计图中获取信息的意识。
18.(1)7分米
(2)9段
【分析】(1)要把两根彩带截成同样长的短彩带且没有剩余,求截成的短彩带最长是多少厘米,就是求28和35的最大公因数,根据求两个数的最大公因数方法:两个数的公有质因数连乘积,就是这两个数的最大公因数,据此求出截成的短彩带的长度;
(2)再用两条彩带的长度和除以每段截成的长度,即可求出一共可以截成多少段这样的彩带条。
【详解】(1)28=2×2×7
35=5×7
28和35的最大公因数是7,截成的短彩带最长是7分米。
答:截成的短彩带最长是7分米。
(2)(28+35)÷7
=63÷7
=9(段)
答:一共可以截成9段这样的短彩带。
【点睛】熟练掌握求两个数的最大公因数的方法是解答本题的关键。
19.(1)30人;
(2)6人
【分析】(1)要求小班的小朋友至少有多少人,实质是求10和6的最小公倍数。求最小公倍数是共有质因数与独有质因数的连乘积,对于两个数来说:两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数,由此解决问题即可;
(2)因为方阵总人数=每边人数×每边人数,所以排成一个正方形方阵的人数,是一个完全平方数,42=16;52=25,62=36,因为小朋友至少有30人,由此即可解答。
【详解】(1)
2×5×3
=10×3
=30(人)
答:小朋友至少有30人。
(2)62=36(人)
36-30=6(人)
答:至少增加6人。
【点睛】此题主要考查求两个数的最小公倍数的方法:两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数;解答此题关键是明确如果要站成方队,则方队的总人数应是完全平方数。
20.
所以用3厘米做正方形的边长。
(个)
(个)
(个)
作图见详解。
能分成6个这样的正方形。
【分析】通过观察发现,这个长方形的长为9厘米,宽为6厘米,9和6 的最大公因数是3,用3厘米作正方形的边长。求出一共能分成多少个正方形。
【详解】9=3×3
6=2×3
所以用3厘米做正方形的边长。
9÷3=3(个)
6÷3=2(个)
3×2=6(个)
能分成6个这样的正方形。
【点睛】解决本题得关键是找到长和宽的最大公因数。
21.表见详解
6时40分
【分析】由于901路汽车每8分钟发车一次,k6路汽车每20分钟发车一次,两个车都是6点出发,那么把两个车发车的时间依次写出来,然后找第二次能够相同出发的时间即可。
【详解】由分析可知:
901路
路
答:第二次同时发车是在6时40分。
【点睛】本题主要考查最小公倍数的找法,解题的关键是把它们发车的时间依次列出。
22.16盆
【分析】本题属于两端都要放的问题,先求出第一盆到最后一盆花的总距离是(46-1)×2=90米;又因为2和3的最小公倍数是6,所以每隔6米处的花盆不用动,据此解答。
【详解】(46-1)×2
=45×2
=90(米)
2和3的最小公倍数是2×3=6
所以每隔6米出的花盆不用移动。
90÷6=15(盆)
15+1=16(盆)
答:有16盆花不需要移动。
【点睛】本题考查植树问题,以及利用两个数的最小公倍数解决实际问题的灵活运用,这里要注意加上开头的第一盆花也不移动。
23.5月13日他们又再次相遇。
【分析】由题意可知,小明每6天去一次,小华每9天去一次,6和9的最小公倍数就是他们相遇两次之间间隔的时间;从4月25日向后推算这个天数即可。
【详解】6=2×3,9=3×3
6和9的最小公倍数是:2×3×3=18
所以他们每相隔18天见一次面
4月还有:30-25=5(天)
5月还要:18-5=13(天)
4月25日再过18天是5月13日
答:5月13日他们又再次相遇。
【点睛】本题关键是找出他们每两次相遇之间相隔的天数,进而根据开始的天数推算求解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第1-3单元重难点应用题达标练习-数学五年级下册苏教版
1.学校买来一批篮球和足球,篮球的个数是足球的5倍,篮球的个数比足球多32个。学校买来篮球和足球各多少个?
2.电冰箱厂今年计划生产冰箱72万台,比去年产量的2倍少6万台。去年生产冰箱多少万台?(列方程并解答)
3.学校图书馆有故事书、科技书和美术书共410本,科技书比故事书少28本,美术书比故事书少69本。三种书各有多少本?(先将下面的线段图补充完整,再解答)
4.小冬原来有一些邮票,今年又收集了35枚,送给小明40枚后,还剩50枚。小冬原来有邮票多少枚?(列方程解答)
5.学校图书馆购进文艺书和科技书共320本,其中文艺书的本数是科技书的4倍,文艺书、科技书各有多少本?(用方程解)
6.甲、乙两艘轮船同时从上海出发开往青岛。经过8小时后,乙船落后甲船24千米。乙船每小时行32.5千米,甲船每小时行多少千米?(用方程法解)
7.成渝高速路长330千米,一辆大客车从重庆开往成都,一辆小轿车同时从成都开往重庆,2小时在途中相遇,已知小轿车的速度是大客车的1.2倍,两车每小时各行多少千米?(用方程解)
8.柏树和松树一共有7500棵。柏树的棵数是松树的1.5倍。两种树各有多少棵?(列方程解答)
9.王方和李亮共收集了128枚邮票。王方送给李亮16枚后两人数量相等。王方原来有邮票多少枚?
10.“夏至”是一年中白昼最长,黑夜最短的一天。这天苏州白昼的时间大约是黑夜的1.4倍,那么这天苏州的白昼时间大约是多少小时?(用方程解)
11.学校一共有120个足球,四年级有4个班,每班借了12个,剩下的借给了五年级的4个班,五年级平均每个班借了多少个?(列方程解答)
12.下表是求知书店和育人书店2017年上半年销售教育类图书的统计表。
(1)请根据上表中的数据完成下面的折线统计图。
(2)求知书店和育人书店分别是哪个月销售图书最多?哪个月两个书店销售图书相差最大?
13.新时代商场2020年下半年空调和冰箱的销售情况如表所示:
7月份 8月份 9月份 10月份 11月份 12月份
空调 450 750 600 350 200 620
冰箱 300 550 450 350 250 200
(1)根据表中数据完成折线统计图。
(2)商场下半年平均每月销售冰箱多少台?
(3)如果每台空调的利润是150元,那么这个商场2020年第三季度空调共获利多少万元?
14.下一星期就要举行全校投篮比赛,每班将推出一名最优选手参赛。五(1)班公认投篮最好两位选手分别小军和小兵,派谁去呢?班主任王老师找出前5周两人进行测试的结果,以统计表和统计图形式呈现,成绩如下:
小军前5周投篮情况统计表:
次数 第1周 第2周 第3周 第4周 第5周
个数 20 12 28 15 30
(1)根据统计表中的数据,按图例在统计图中画出小军投篮情况的折线。
(2)第( )周和第( )周两人投得同样多。
(3)要从两人中选一人代表五(1)班参加全校比赛,你给王老师做参谋,将推选( )去比赛,你的理由是:( )。
15.如表是甲乙两种树生长情况统计表。
(1)根据统计表将下面的统计图补充完整
(2)从开始植树到第七年,生长速度较快的是( )。(填“甲树”或“乙树”)
(3)生长到第( )年,两棵树的高度都是8米。
16.如图是甲、乙两市2018年月平均气温变化情况。
(1)两个城市,( )市可能是南方城市。
(2)乙市( )月平均气温最低,甲市( )月平均气温最高?
(3)有一种植物的生长期为5个月,最适宜的生长温度为这种植物适合在( )市生长。(填“甲”或“乙”)
(4)从统计图中你还得到哪些信息?
17.下面是大同市2021年4月1日~7日气温统计表。(单位:℃)
(1)请你根据表中的数据,完成下面折线统计图。
(2)在4月1日~7日中,( )日气温最低,( )日气温最高。
(3)在4月1日~7日中,温差最大的是( )日,( )日和( )的温差一样。
(4)在4月1日~7日相邻的两天中,从( )日到( )日温度下降最快。
18.把一根长28分米的彩带和一根长35分米的彩带截成同样长的短彩带且没有剩余。
(1)截成的短彩带最长是多少分米?
(2)一共可以截成多少段这样的短彩带?
19.幼儿园小班的小朋友排队做操,10人一排或6人一排都恰好分完。
(1)小朋友至少有多少人?
(2)至少再增加多少人,才能排成正方形的队伍?
20.把下面的方格图(每小格边长看成1厘米)分割成几个面积最大并相等的正方形,且没有剩余。能分成多少个这样的正方形?先写出计算过程,再在图中画出分割过程。
21.姜堰城区至海险城区公交车,901路每8分钟发一辆车,路每20分钟发一辆车,这两路车第一次同时发车时间是早上,第二次同时发车是什么时候?(先列表,再回答)
901路
路
22.新区学校为美化校园,在中心路的一侧放鲜花,共放了46盆,每两盆之间的距离是2米,现在要改成每两盆之间距离是3米,有多少盆花不需要移动?
23.小明和小华两人定期到张奶奶家去打扫卫生。小明每6天去一次,小华每9天去一次。4月25日两人在张奶奶家相遇,几月几日他们又再次相遇?
参考答案:
1.足球有10个;篮球有40个
【分析】根据篮球的个数比足球多32个,可以提炼这道题的等量关系是:篮球的个数-足球的个数=32个,根据这个等量关系,列方程解答。
【详解】解:设足球有x个,篮球有5x个
5x-x=32
4x=32
4x÷4=32÷4
x=8
8×5=40(个)
答:足球有10个,篮球有40个。
【点睛】本题解题关键是找出题目中的等量关系:篮球的个数-足球的个数=32个,列方程解答。
2.39万台
【分析】设去年生产冰箱x万台,今年比去年产量的2倍少6万台,去年生产冰箱的台数×2-6=今年冰箱的台数,列方程:2x-6=72,解方程,即可解答。
【详解】解:设去年生产冰箱x万台。
2x-6=72
2x-6+6=72+6
2x=78
2x÷2=78÷2
x=39
答:去年生产冰箱39万台。
【点睛】本题主要考查运用方程解决问题的能力,解决此类问题一般方法是:根据等量关系列方程,求解。
3.图见解析;故事书:169本;科技书:141本,美术书:100本
【分析】以故事书为标准,画出一条线段,根据科技书比故事书少28本,美术书比故事书少69本,画出科技书和故事书的量是多少即可;
设故事书有x本,科技书比故事书少28本,则科技书有x-28本;美术书比故事书少69本,则美术书有x-69本,故事书、科技书和美术书共410本,即故事书的本数+科技书的本数+美术书的本数=410本,列方程:x+(x-28)+(x-69)=410,解方程,即可解答。
【详解】如图:
;
解:设故事书有x本,则科技书有x-28本,美术书有x-69本。
x+(x-28)+(x-69)=410
x+x-28+x-69=410
3x=410+28+69
3x=438+69
3x=507
x=507÷3
x=169
科技书:169-28=141(本)
美术书:169-69=100(本)
答:故事书有169本,科技书有141本,美术书有100本。
【点睛】本题考查方程的实际应用,根据三种书的数量关系,设出未知数,找出相关的量。列方程,解方程。
4.
55枚
【分析】设小冬原来有邮票x枚,根据题意:原来的邮票+35-40=50,据此列方程求解。
【详解】解:设小冬原来有邮票x枚。
x+35-40=50
x=50+40-35
x=90-35
x=55
答:小冬原来有邮票55枚。
【点睛】解答本题的关键是认真读题,找准关系式,即:原来的邮票+35-40=50。
5.文艺书:256本;科技数64本
【分析】设科技书有x本,则文艺书有4x本;根据文艺书和科技书共320本列出方程求出科技书的本数,进而得出文艺书的本数;据此解答。
【详解】解:设科技书有x本,则文艺书有4x本。
x+4x=320
5x=320
5x÷5=320÷5
x=64
4x=4×64=256
答:文艺书有256本,科技数有64本。
【点睛】本题主要考查列方程解含有两个未知数的问题,找出等量关系式是解题的关键。
6.35.5千米
【分析】设甲船每小时行x千米,根据“速度差×时间=路程差”列出方程求解即可。
【详解】解:设甲船每小时行x千米
(x-32.5)×8=24
(x-32.5)×8÷8=24÷8
x-32.5=3
x-32.5+32.5=3+32.5
x=35.5
答:甲船每小时行35.5千米。
【点睛】本题主要考查应用方程解简单的行程问题,明确“速度差×时间=路程差”是解题的关键。
7.大客车:75千米;小轿车:90千米
【分析】根据题意,小轿车的速度是大客车的1.2倍,即大客车的速度×1.2=小轿车的速度;设大客车每小时行x千米,则小轿车每小时行1.2x千米;大客车2小时行驶2x千米;小轿车2小时行驶1.2x×2千米,两车行驶的路程和等于成渝高速路的长度,列方程:2x+1.2x×2=330,解方程,即可解答。
【详解】解:设大客车每小时行x千米,则小轿车每小时1.2x千米。
2x+1.2x×2=330
2x+2.4x=330
4.4x=330
x=330÷4.4
x=75
小轿车:75×1.2=90(千米)
答:大客车每小时行75千米,小轿车每小时行90千米。
【点睛】本题考查方程的实际应用,根据大客车每小时行驶的路程和小轿车每小时行驶的路程,设出未知数,找出相关的量,列方程,解方程。
8.松树:3000棵;柏树:4500棵。
【分析】设松树有x棵,柏树的棵数是松树的1.5倍,则柏树有1.5x棵;柏树和松树一共有7500棵,即柏树棵数+松树棵数=7500,列方程:1.5x+x=7500,解方程,即可解答。
【详解】解:设松树有x棵,则柏树有1.5x棵。
1.5x+x=7500
2.5x=7500
x÷2.5=7500÷2.5
x=3000
3000×1.5=4500(棵)
答:松树有3000棵,柏树有4500棵。
【点睛】本题考查方程的实际应用,根据松树棵数和柏树棵数之间的关系,设出未知数,找出相关的量,列方程,解方程。
9.80枚
【分析】假设王方原来有邮票x枚,则李亮有(128-x)枚邮票,根据数量关系:王方邮票的数量-16=李亮邮票的数量+16,代入列出方程,解方程即可求出王方原来有多少枚邮票。
【详解】解:设王方原来有邮票x枚,则李亮有(128-x)枚邮票,
x-16=128-x+16
x+x=128+16+16
2x=160
x=80
答:王方原来有邮票80枚。
【点睛】此题的解题关键是弄清题意,把王方原来的邮票数设为未知数x,找出题中数量间的相等关系,列出包含x的等式,解方程得到最终的结果。
10.14小时
【分析】设这天苏州的黑夜时间大约是x小时,则白昼时间大约是1.4x小时,根据白昼时间+黑夜时间=24小时,列方程求解即可。
【详解】解:设这天苏州的黑夜时间大约是x小时。
1.4x+x=24
2.4x=24
x=10
1.4×10=14(小时)
答:这天苏州的白昼时间大约是14小时。
【点睛】本题主要考查列方程解含有两个未知数的问题,找出等量关系式是解题的关键。
11.18个
【分析】根据题干,设五年级平均每班借x个,则根据等量关系:四年级每班借的个数×班级数+五年级平均每班借的个数×班级数=学校足球的总个数,据此列出方程即可解决问题。
【详解】解:设五年级平均每班借x个。
12×4+4x=120
48+4x=120
48+4x-48=120-48
4x=72
4x÷4=72÷4
x=18
答:五年级平均每班借了18个。
【点睛】解答此题关键是找出数量之间的相等关系,由此列方程解答即可。
12.(1)见详解;
(2)求知书店4月份;育人书店3月份;6月份相差最大
【分析】(1)根据表中数据描点连线即可完成折线统计图;
(2)观察折线统计图,实线表示求知书店,虚线表示育人书店,找出折线最高点,此时对应的月份就是销售图书最多的月份;找出实线虚线相差最大的处,此时对应的月份就是销售图书相差最大的月份。
【详解】(1)折线统计图如下:
(2)观察折线统计图可知:求知书店4月份销售图书最多;育人书店3月份销售图书最多;6月份两个书店销售图书相差最大。
【点睛】本题主要考查统计图表的综合应用,根据表中数据画出统计图是解题的关键。
13.(1)见详解。
(2)台
(3)27万元
【分析】(1)根据统计表所提供的数据,在统计图中描出空调和冰箱销售量的点,顺次连接,标上数据等即可完成折线统计图;
(2)首先求出2020年下半年一共销售冰箱多少台;然后用它除以6,求出平均每月销售冰箱多少台即可;
(3)首先求出2020年第三季度一共销售空调多少台;然后用它乘每台冰箱获利的钱数即可。
【详解】(1)画图如下:
(2)(300+550+450+350+250+200)÷6
=2100÷6
=350(台)
答:商场下半年平均每月销售冰箱350台。
(3)(450+750+600)×150
=1800×150
=270000(元)
270000元=27万元
答:这个商场2020年第三季度空调共获利27万元。
【点睛】此题主要考查的了如何根据统计表所提供的数据绘制折线统计图、观察折线统计图,从图中获取信息,并利用获取的信息解题的能力。
14.(1)见详解
(2)2,5
(3)小兵,他的发挥比小军稳定
【分析】(1)按照小军前5周的投篮个数数描出各点,再用线段依次连接,最后在点上标出数据。
(2)观察统计图可知,第2周两人都踢了12个,第5周两人都投了30个,据此解答。
(3)表示小军投篮个数的曲线起伏较大,说明小军发挥不稳定;小兵的投篮个数程上升趋势,发挥稳定。据此解答。
【详解】(1)
(2)第2周和第5周两人投得同样多。
(3)要从两人中选一人代表五(1)班参加全校比赛,将推选小兵去比赛,你的理由是:他的发挥比小军稳定。
【点睛】本题考查复式折线统计图的应用。观察统计图,找出需要的信息是解题的关键。
15.(1)见详解
(2)乙树
(3)10
【分析】(1)根据统计表提供的数据,完成统计图;
(2)观察统计图第七年后,哪种树生长的快;
(3)观察统计图,找出第几年两棵树的高度都是8米。
【详解】(1)
(2)从开始植树到第七年,生产速度较快的是乙树;
(3)生长到第10年,两个数的高度都是8米。
【点睛】本题考查折线统计图的填充。关键是利用所给数据完成统计图并回答问题。
16.(1)甲
(2)1;8
(3)甲
(4)甲市1月平均气温比乙市高15度。
【分析】(1)甲市平均气温较高,乙市平均气温偏低,根据我国南方城市气温高北方城市气温低的特点判断;
(2)乙市1月气温数据在最低点。甲市8月数据在最高点;
(3)乙市平均气温最高25度,相比甲市5-10月气温更适合这种植物生长;
(4)统计图中能得到很多信息:如甲市1月平均气温比乙市高15度。
【详解】(1)根据我国气温南高北低的特点,甲市可能是南方城市。
(2)乙市1月份数据最小,甲市8月数据最大。
乙市1月平均气温最低,甲市8月平均气温最高。
(3)甲市5-10月平均气温在25度-32.5度之间,乙市平均气温最高在25度,这种植物适合甲市生长。
(4)从统计图中还得到很多信息。如甲市1月平均气温比乙市高15度。(答案不唯一)
【点睛】本题为复式折线统计图,分析统计图中数据,根据统计图的数据解决问题。
17.(1)见详解。
(2)3;1
(3)2;3;4
(4)2;3
【分析】(1)制作折线统计图时,先从列中找到项目,再从行中找到对应的数量高度点个点,然后顺次连点成线,复式图虚实线分开表示。
(2)比较在4月1日~7日中各天的最高和最低气温,作判断。
(3)比较在4月1日~7日中每天的温差,作判断。
(4)比较4月1日~7日相邻的两天中气温下降最大的,作判断。
【详解】(1)如图:
(2)在4月1日~7日中,3日气温最低,1日气温最高。
(3)15-2=13℃
13-(﹣2)=15℃
7-(﹣3)=10℃
12-2=10℃
14-0=14℃
11-3=8℃
13-1=12℃
答:在4月1日~7日中,温差最大的是2日,3日和4的温差一样。
(4)在4月1日~7日相邻的两天中,从2日到3日温度下降最快。
【点睛】本题考查了学生动手操作能力及从统计图中获取信息的意识。
18.(1)7分米
(2)9段
【分析】(1)要把两根彩带截成同样长的短彩带且没有剩余,求截成的短彩带最长是多少厘米,就是求28和35的最大公因数,根据求两个数的最大公因数方法:两个数的公有质因数连乘积,就是这两个数的最大公因数,据此求出截成的短彩带的长度;
(2)再用两条彩带的长度和除以每段截成的长度,即可求出一共可以截成多少段这样的彩带条。
【详解】(1)28=2×2×7
35=5×7
28和35的最大公因数是7,截成的短彩带最长是7分米。
答:截成的短彩带最长是7分米。
(2)(28+35)÷7
=63÷7
=9(段)
答:一共可以截成9段这样的短彩带。
【点睛】熟练掌握求两个数的最大公因数的方法是解答本题的关键。
19.(1)30人;
(2)6人
【分析】(1)要求小班的小朋友至少有多少人,实质是求10和6的最小公倍数。求最小公倍数是共有质因数与独有质因数的连乘积,对于两个数来说:两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数,由此解决问题即可;
(2)因为方阵总人数=每边人数×每边人数,所以排成一个正方形方阵的人数,是一个完全平方数,42=16;52=25,62=36,因为小朋友至少有30人,由此即可解答。
【详解】(1)
2×5×3
=10×3
=30(人)
答:小朋友至少有30人。
(2)62=36(人)
36-30=6(人)
答:至少增加6人。
【点睛】此题主要考查求两个数的最小公倍数的方法:两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数;解答此题关键是明确如果要站成方队,则方队的总人数应是完全平方数。
20.
所以用3厘米做正方形的边长。
(个)
(个)
(个)
作图见详解。
能分成6个这样的正方形。
【分析】通过观察发现,这个长方形的长为9厘米,宽为6厘米,9和6 的最大公因数是3,用3厘米作正方形的边长。求出一共能分成多少个正方形。
【详解】9=3×3
6=2×3
所以用3厘米做正方形的边长。
9÷3=3(个)
6÷3=2(个)
3×2=6(个)
能分成6个这样的正方形。
【点睛】解决本题得关键是找到长和宽的最大公因数。
21.表见详解
6时40分
【分析】由于901路汽车每8分钟发车一次,k6路汽车每20分钟发车一次,两个车都是6点出发,那么把两个车发车的时间依次写出来,然后找第二次能够相同出发的时间即可。
【详解】由分析可知:
901路
路
答:第二次同时发车是在6时40分。
【点睛】本题主要考查最小公倍数的找法,解题的关键是把它们发车的时间依次列出。
22.16盆
【分析】本题属于两端都要放的问题,先求出第一盆到最后一盆花的总距离是(46-1)×2=90米;又因为2和3的最小公倍数是6,所以每隔6米处的花盆不用动,据此解答。
【详解】(46-1)×2
=45×2
=90(米)
2和3的最小公倍数是2×3=6
所以每隔6米出的花盆不用移动。
90÷6=15(盆)
15+1=16(盆)
答:有16盆花不需要移动。
【点睛】本题考查植树问题,以及利用两个数的最小公倍数解决实际问题的灵活运用,这里要注意加上开头的第一盆花也不移动。
23.5月13日他们又再次相遇。
【分析】由题意可知,小明每6天去一次,小华每9天去一次,6和9的最小公倍数就是他们相遇两次之间间隔的时间;从4月25日向后推算这个天数即可。
【详解】6=2×3,9=3×3
6和9的最小公倍数是:2×3×3=18
所以他们每相隔18天见一次面
4月还有:30-25=5(天)
5月还要:18-5=13(天)
4月25日再过18天是5月13日
答:5月13日他们又再次相遇。
【点睛】本题关键是找出他们每两次相遇之间相隔的天数,进而根据开始的天数推算求解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
