2.2圆周角——圆内接四边形 课件
图片预览







文档简介
课件20张PPT。圆周角第2课时邵阳市第十五中学
彭雯
2018年12月1日11时36分复习引入1、圆周角定理:圆周角的度数等于它所对的 上的圆心角度数的 。
2、弧的度数等于它所对的 的度数。
3、100o的弧所对的圆心角等于_______,所对的圆周角等于_______。
4、如图,在⊙O中,∠BAC=32o,则∠BOC=______
弧一半圆心角100°50°64°AB是⊙O的直径,那么∠C1,∠C2,∠C3的度数分别为多少?直径所对的圆周角是直角探究活动一【探究一】如图,A、B、C为圆周上三点,若已知∠C=90°,它所对的弦AB是不是直径?要求:1、先猜想,再证明
2、同桌之间合作探究
3、总结做题的方法规律
时间:2分钟探究活动一直径所对的圆周角是直角;
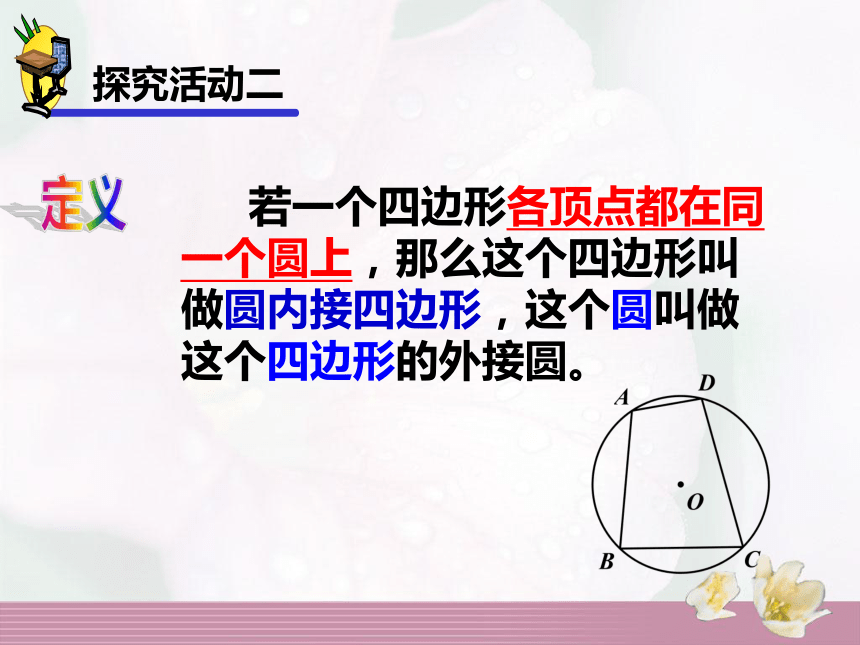
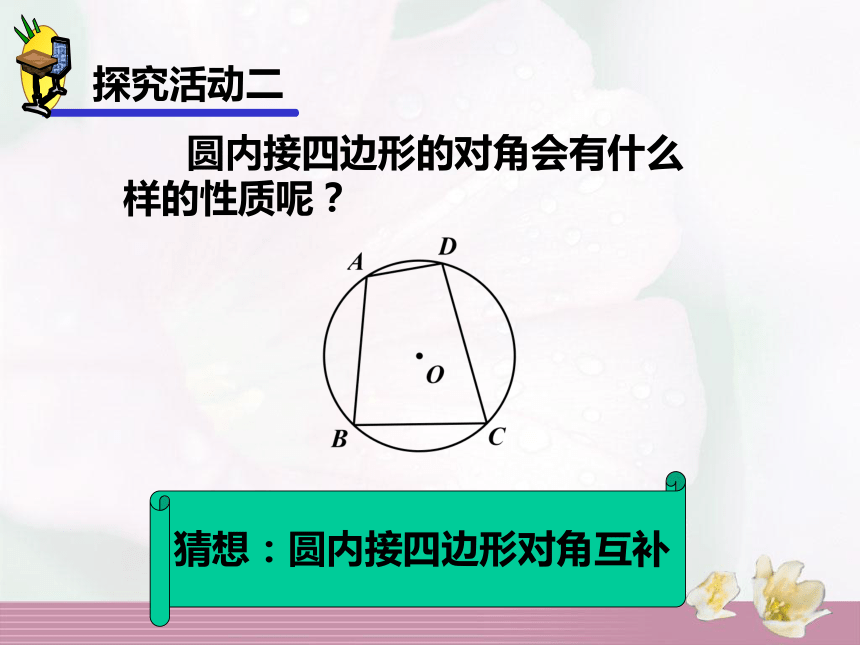
90°的圆周角所对的弦是直径探究活动一圆周角定理的推论探究活动二 麦田怪圈(Crop Circle)通常是麦田经过暴风骤雨的洗礼一夜之间形成,至今无法解释是何种方式形成的圆内接四边形 若一个四边形各顶点都在同一个圆上,那么这个四边形叫做圆内接四边形,这个圆叫做这个四边形的外接圆。探究活动二定义 圆内接四边形的对角会有什么样的性质呢?探究活动二圆内接四边形的对角互补?已知:如图,四边形ABCD是圆内接四边形。求证: ∠A+ ∠C=180°
∠B +∠D=180°探究活动二要求:1、四人一组,分组讨论
2、每组两人上台展示,其中一人展示板
书,另一人讲解思路
3、总结做题的方法规律
时间:3分钟圆内接四边形的对角互补?已知:如图,四边形ABCD是圆内接四边形。求证: ∠A+ ∠C=180°
∠B +∠D=180°证明:连接OB,OD
∵∠A所对的弧为BCD,∠C所对的弧为BAD
又BCD与BAD所对的圆心角之和是周角
∴∠A+∠C=360°÷ 2 =180°
由四边形内角和定理知:∠ABC+∠ADC=180°))))探究活动二 延长BC至点E,∠A和∠DCE有什么数量关系?解:∵四边形ABCD是圆内接四边形
∴∠DCB+∠A=180°
又∵∠DCE+∠DCB=180°
∴∠DCE=∠A圆内接四边形任意一个外角都等于它的内对角.变式训练E探究活动二∵四边形ABCD是圆内接四边形,∴∠A+∠ C= 180°∠B+∠D=180°圆内接四边形的对角互补.圆内接四边形的性质定理:符号语言:圆内接四边形任意一个外角都等于它的内对角.探究活动二结论推论XXX
(1)相等的圆周角所对的弧也相等。( )
(2)90。的角所对的弦是直径。 ( )
(3)同弦所对的圆周角相等。 ( )
(4)圆内接平行四边形是矩形 ( )判断对错√如图,四边形ABCD为?O的内接四边形,已知∠BOD为100°,则
∠BAD= ,∠BCD= .填一填50°130° 如图,AB是⊙O的直径,∠A=80°. ∠ABC= . 填一填10° 如图,AB是⊙O的直径,BD是弦,延长BD到C,使AC=AB,BD与CD的大小有什么关系?为什么?理由是:连接AD
∵AB是⊙O的直径
∴∠ADB=90°
即AD⊥BC
又∵AC=AB
∴BD=CD(三线合一)解: BD=CD试一试如图,四边形ABCD内接于⊙O,如果∠BOD=130°,则∠BCD的度数是( )
A、115° B、130°
C、65° D、50°
如图,等边三角形ABC内接于⊙O,P是弧AB上的 一点,则∠APB= 。
A120°做一做课堂小结 本节课我们学习了圆周角定理的哪些推论?1、直径所对的圆周角是直角;90°的圆周角所对的弦是直径
2、圆内接四边形对角互补,圆内接四边形任意一个外角都等于它的内对角.做辅助线常用方法:构造直径上的圆周角如图,?O1和?O2都经过A、B两点,经过点A的直线CD与?O1交于点C,与?O2交于点D,经过点B的直线EF与?O1交于点E,与?O2交于点F。求证:CE∥DF拓展提升证明:连接AB
∵四边形ACEB是?O1的内接四边形
∴∠C+∠ABE=180°
同理可证∠ABF+∠D=180°
又∵∠ABE+∠ABF=180°
∴∠C+∠D=180°
∴CE∥DF
彭雯
2018年12月1日11时36分复习引入1、圆周角定理:圆周角的度数等于它所对的 上的圆心角度数的 。
2、弧的度数等于它所对的 的度数。
3、100o的弧所对的圆心角等于_______,所对的圆周角等于_______。
4、如图,在⊙O中,∠BAC=32o,则∠BOC=______
弧一半圆心角100°50°64°AB是⊙O的直径,那么∠C1,∠C2,∠C3的度数分别为多少?直径所对的圆周角是直角探究活动一【探究一】如图,A、B、C为圆周上三点,若已知∠C=90°,它所对的弦AB是不是直径?要求:1、先猜想,再证明
2、同桌之间合作探究
3、总结做题的方法规律
时间:2分钟探究活动一直径所对的圆周角是直角;
90°的圆周角所对的弦是直径探究活动一圆周角定理的推论探究活动二 麦田怪圈(Crop Circle)通常是麦田经过暴风骤雨的洗礼一夜之间形成,至今无法解释是何种方式形成的圆内接四边形 若一个四边形各顶点都在同一个圆上,那么这个四边形叫做圆内接四边形,这个圆叫做这个四边形的外接圆。探究活动二定义 圆内接四边形的对角会有什么样的性质呢?探究活动二圆内接四边形的对角互补?已知:如图,四边形ABCD是圆内接四边形。求证: ∠A+ ∠C=180°
∠B +∠D=180°探究活动二要求:1、四人一组,分组讨论
2、每组两人上台展示,其中一人展示板
书,另一人讲解思路
3、总结做题的方法规律
时间:3分钟圆内接四边形的对角互补?已知:如图,四边形ABCD是圆内接四边形。求证: ∠A+ ∠C=180°
∠B +∠D=180°证明:连接OB,OD
∵∠A所对的弧为BCD,∠C所对的弧为BAD
又BCD与BAD所对的圆心角之和是周角
∴∠A+∠C=360°÷ 2 =180°
由四边形内角和定理知:∠ABC+∠ADC=180°))))探究活动二 延长BC至点E,∠A和∠DCE有什么数量关系?解:∵四边形ABCD是圆内接四边形
∴∠DCB+∠A=180°
又∵∠DCE+∠DCB=180°
∴∠DCE=∠A圆内接四边形任意一个外角都等于它的内对角.变式训练E探究活动二∵四边形ABCD是圆内接四边形,∴∠A+∠ C= 180°∠B+∠D=180°圆内接四边形的对角互补.圆内接四边形的性质定理:符号语言:圆内接四边形任意一个外角都等于它的内对角.探究活动二结论推论XXX
(1)相等的圆周角所对的弧也相等。( )
(2)90。的角所对的弦是直径。 ( )
(3)同弦所对的圆周角相等。 ( )
(4)圆内接平行四边形是矩形 ( )判断对错√如图,四边形ABCD为?O的内接四边形,已知∠BOD为100°,则
∠BAD= ,∠BCD= .填一填50°130° 如图,AB是⊙O的直径,∠A=80°. ∠ABC= . 填一填10° 如图,AB是⊙O的直径,BD是弦,延长BD到C,使AC=AB,BD与CD的大小有什么关系?为什么?理由是:连接AD
∵AB是⊙O的直径
∴∠ADB=90°
即AD⊥BC
又∵AC=AB
∴BD=CD(三线合一)解: BD=CD试一试如图,四边形ABCD内接于⊙O,如果∠BOD=130°,则∠BCD的度数是( )
A、115° B、130°
C、65° D、50°
如图,等边三角形ABC内接于⊙O,P是弧AB上的 一点,则∠APB= 。
A120°做一做课堂小结 本节课我们学习了圆周角定理的哪些推论?1、直径所对的圆周角是直角;90°的圆周角所对的弦是直径
2、圆内接四边形对角互补,圆内接四边形任意一个外角都等于它的内对角.做辅助线常用方法:构造直径上的圆周角如图,?O1和?O2都经过A、B两点,经过点A的直线CD与?O1交于点C,与?O2交于点D,经过点B的直线EF与?O1交于点E,与?O2交于点F。求证:CE∥DF拓展提升证明:连接AB
∵四边形ACEB是?O1的内接四边形
∴∠C+∠ABE=180°
同理可证∠ABF+∠D=180°
又∵∠ABE+∠ABF=180°
∴∠C+∠D=180°
∴CE∥DF
