【多媒体导学案】人教版数学八年级上册第十三章第1课时 轴对称(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学八年级上册第十三章第1课时 轴对称(教师版) |

|
|
| 格式 | zip | ||
| 文件大小 | 427.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-10 10:38:44 | ||
图片预览



文档简介
一、学习目标 1.理解什么是轴对称图形;2.理解什么是“两个图形关于一条直线对称”;3.能够说出轴对称与轴对称图形的区别与联系.
二、知识回顾 1.如图(1),OC平分∠AOB,则∠AOC= ∠BOC = ∠AOB . ( http: / / www.21cnjy.com )2.如图(2),△ABD≌△ACD,AB与AC是对应边.写出这两个三角形的对应顶点和对应边. ( http: / / www.21cnjy.com )对应顶点: A与A;B与C;D与D. 对应边: AD与AD;BD与CD.
三、新知讲解 1.轴对称图形如果一个图形沿一条直线折叠,直线两旁的部分能够 互相重合 ,这个图形就叫做 轴对称图形 ,这条直线就是它的 对称轴 .2.成轴对称的两个图形把一个图形沿着某一条直线 折叠 ,如 ( http: / / www.21cnjy.com )果它能够与另一个图形 重合 ,那么就说这两个图形关于这条直线(成轴)对称,这条直线叫做 对称轴 ,折叠后重合的点是对应点,叫做 对称点 .3.轴对称图形与成轴对称的两个图形的区别与联系:区别一个具有特殊形状的图形,至少有一条对称轴.两个图形的位置关系,只有一条对称轴.联系如果把轴对称图形沿对称轴分成两部分,那么这两部分就是这条直线成轴对称.如果把两个成轴对称的图形拼在一起,看成一个整体,那么它就是一个轴对称图形.4.线段的垂直平分线经过线段中点并且垂直这条线段的直线,叫做这条线段的 垂直平分线 .5.轴对称的性质:(1)成轴对称的两个图形全等.(2)如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连接线段的垂直平分线.类似地,轴对称图形的对称轴,是任何一对对应点所连接线段的垂直平分线.(3)两个图形关于某条直线对称,如果他们的对应线段或其延长线相交,那么交点一定在对称轴上.
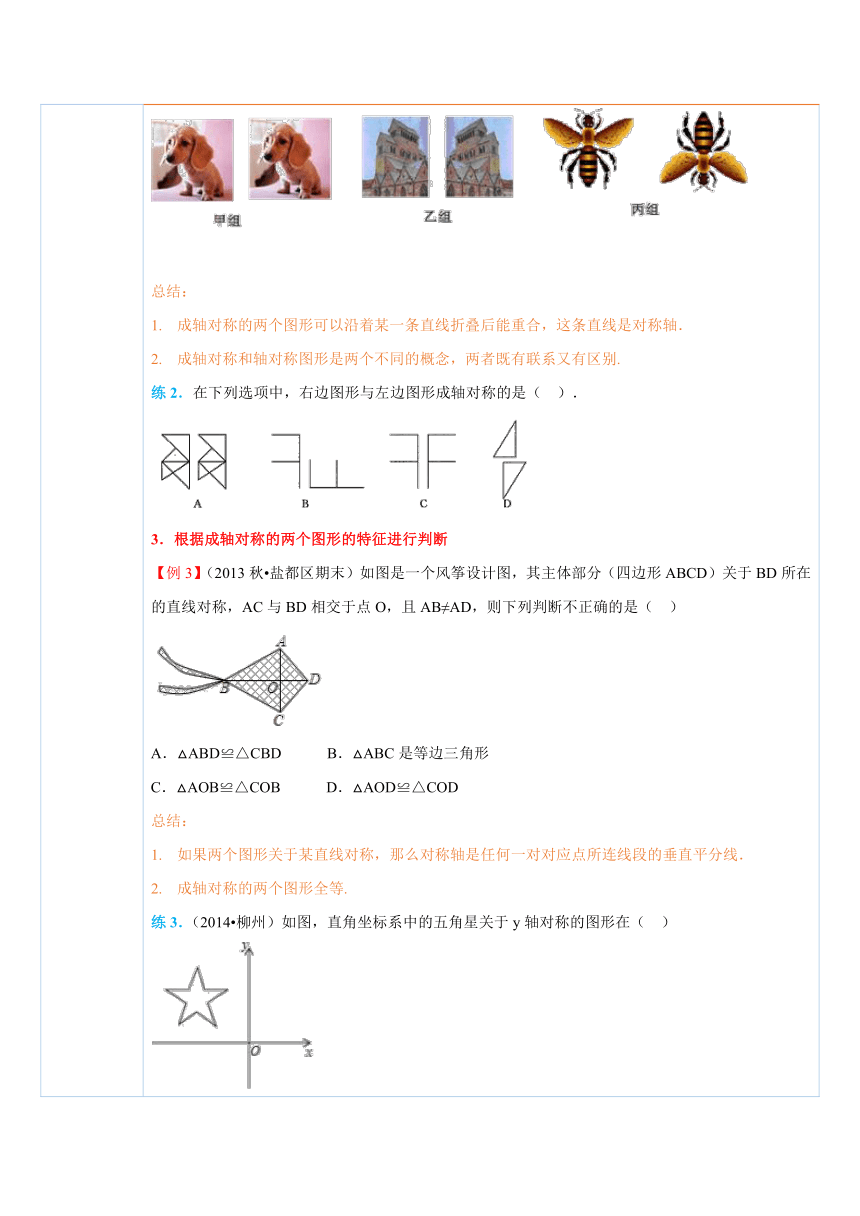
四、典例探究 扫一扫,有惊喜哦!1.轴对称几何图形的识别【例1】(2015 乐陵市模拟)如图,图中的图形是常见的安全标记,其中是轴对称图形的是()A. ( http: / / www.21cnjy.com ) B. C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )总结:判断一个图形是轴对称图形的关键是寻找到对称 ( http: / / www.21cnjy.com )轴. 如果有一条直线,使得图形两部分折叠后可重合,那么这个图形就是轴对称图形,这条直线就是对称轴.几何图形中的线段、角、正方形、长方形、等腰三角形、等腰梯形、圆等都是轴对称图形.练1.如图,国旗是一个国家的象征,观察下面的国旗,是轴对称图形的是().A.加拿大、澳大利亚、乌拉圭 B.加拿大、澳大利亚、瑞典C.加拿大、瑞典、瑞士 D.乌拉圭、瑞典、瑞士2.识别成轴对称的两个图形【例2】下面给出的每组照片中的两个图案成轴对称吗?如果是,试着找出它们的对称轴,并找出一对对称点. ( http: / / www.21cnjy.com )总结:成轴对称的两个图形可以沿着某一条直线折叠后能重合,这条直线是对称轴.成轴对称和轴对称图形是两个不同的概念,两者既有联系又有区别.练2.在下列选项中,右边图形与左边图形成轴对称的是( ). ( http: / / www.21cnjy.com )3.根据成轴对称的两个图形的特征进行判断【例3】(2013秋 盐都区期末)如图是一 ( http: / / www.21cnjy.com )个风筝设计图,其主体部分(四边形ABCD)关于BD所在的直线对称,AC与BD相交于点O,且AB≠AD,则下列判断不正确的是( ) ( http: / / www.21cnjy.com )A.△ABD≌△CBD B.△ABC是等边三角形C.△AOB≌△COB D.△AOD≌△COD总结:如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.成轴对称的两个图形全等.练3.(2014 柳州)如图,直角坐标系中的五角星关于y轴对称的图形在( ) ( http: / / www.21cnjy.com )A.第一象限 B.第二象限 C.第三象限 D.第四象限4.根据成轴对称的两个图形的特征进行求解【例4】(2015 温州一模)如图,若 ABCD与 BCFE关于BC所在直线对称,∠ABE=86°,则∠E等于( ) ( http: / / www.21cnjy.com )A.137° B.104° C.94° D.86°总结:成轴对称的两个图形的对应边相等、对应角相等.对称轴上的任何一点到两个对应点之间的距离相等.练4.(2014秋 扶余县期中)如图,两个四边形关于直线l对称,∠C=90°,试写出a,b的长度,并求出∠G的度数. ( http: / / www.21cnjy.com )
五、课后小测 一、选择题1.(2013秋 仪征市校级期末)圆是轴对称图形,它的对称轴有()A.1条 B.2条 C.3条 D.无数条2.下列说法错误的是()A.若A,A′是以BC为轴对称的点,则AA′垂直平分BCB.线段的一条对称轴是它本身所在的直线C.一条线段的一个端点的对称点是另一个端点D.等边三角形是轴对称图形3.下列说法错误的是()A.等边三角形有3条对称轴 B.正方形有4条对称轴C.角的对称轴有2条 D.圆有无数条对称轴4.(2015 潍坊模拟)下列图形中,不是轴对称图形的是()A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )5.(2015 伊春模拟)下列体育运动标志中,从图案看不是轴对称图形的有()个. ( http: / / www.21cnjy.com )A.4 B.3 C.2 D.16.(2015 杭州模拟)下面四幅画分别是体育运动长鼓舞,武术,举重、摔跤抽象出来的简笔画,其中是轴对称图形的是()A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )7.(2015 南开区一模)下列四个图形中,轴对称图形有() ( http: / / www.21cnjy.com )A.4个 B.3个 C.2个 D.1个8.(2014秋 厦门期末)如图,△ABC和△A′B′C′关于直线l对称,若∠A=50°,∠C′=30°,则∠B的度数为() ( http: / / www.21cnjy.com )A.30° B.50° C.90° D.100°9.(2014秋 孝南区期末)如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠B=40゜,∠CAD=60゜,则∠BCD=() ( http: / / www.21cnjy.com )A.160゜ B.120゜ C.80゜ D.100゜10.(2014秋 石家庄期末)下列图形中,△A′B′C′与△ABC成轴对称的是()A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )11.(2014春 环翠区校级期末)下列说法中,正确的是()A.到直线l的距离相等的两点关于直线l对称B.角的两边关于角的平分线对称C.圆是轴对称图形,有无数条对称轴D.有一个内角为60°的三角形是轴对称图形12.(2014春 宜宾校级期末)如图,△ABC关于直线a对称,则∠F的度数是() ( http: / / www.21cnjy.com )A.30° B.50° C.90° D.100°二、填空题13.观察下图中各组图形,其中成轴对称的为___________(只写序号1,2等). ( http: / / www.21cnjy.com )14.(2013 上海模拟 ( http: / / www.21cnjy.com ))如图,AB左边是计算器上的数字“5”,若以直线AB为对称轴,那么它的轴对称图形是数字________________. ( http: / / www.21cnjy.com )15.(2010春 海曙区期末)下列图形中,轴对称图形有__________个.16.(2010秋 景洪市校级期末)如图所示,观察规律并填空:空格处应该是_______.17.(2009秋 南京期中)线段、角、平行四边形、长方形、等腰梯形中有两条对称轴的是_____.三、解答题18.(2013秋 赣县校级期中)如图,在下面一组图形符号中找出它们所蕴含的内在规律,然后在横线上的空白处填上恰当的图形. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】根据轴对称图形的概念: ( http: / / www.21cnjy.com )如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形.据此对常见的安全标记图形进行判断.
解:A、有一条对称轴,是轴对称图形,符合题意;
B、不是轴对称图形,因为找不到任何一条直线,使它沿这条直线折叠后,直线两旁的部分能够重合,即不满足轴对称图形的定义.不符合题意;
C、不是轴对称图形,因为找不到任何一条直线,使它沿这条直线折叠后,直线两旁的部分能够重合,即不满足轴对称图形的定义.不符合题意;
D、不是轴对称图形,因为找不到任何一条直线,使它沿这条直线折叠后,直线两旁的部分能够重合,即不满足轴对称图形的定义.不符合题意.
故选A.
练1.【解析】根据轴对称图形的定义,加拿大、瑞典、瑞士的国旗是轴对称图形,故选C.
【例2】【解析】甲组是两幅相同的图案,但不成轴对称;
乙组的两个图形,把其中的一个图形折叠后可以与另一个图形重合,那么这个两个图案成轴对称,其对称轴如图所示;
( http: / / www.21cnjy.com )
丙组的两个图案不成轴对称.
练2.【解析】C的两个图形沿线折叠后重合,根据成轴对称的两个图形的定义,故选C.
【例3】【解析】先根据轴对称的性质得出AB=BC,AD=CD,OA=OC,BD⊥AC,再根据全等三角形的判定定理即可得出结论.
解:∵主体部分(四边形ABCD)关于BD所在的直线对称,AC与BD相交于点O,
∴AB=BC,AD=CD,OA=OC,BD⊥AC,
在△ABD与△CBD中,
,
∴△ABD与△CBD,故A正确;
在△AOB与△COB中,
∴△AOB≌△COB,故C正确;
在△AOD与△COD中,
,
∴△AOD≌△COD,故D正确;
△ABC是等腰三角形,故B错误.
故选:B.
点评:本题考查的是轴对称的性质,熟知如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线是解答此题的关键.
练3.【解析】根据轴对称的性质作出选择.
解:如图所示,直角坐标系中的五角星关于y轴对称的图形在第一象限.
故选:A.
( http: / / www.21cnjy.com )
点评:本题考查了轴对称的性质.此题难度不大,采用了“数形结合”的数学思想.
【例4】【解析】根据轴对称的性质可得∠ABC=∠EBC,然后求出∠EBC,再根据平行四边形邻角互补列式计算即可得解.
解:∵ ABCD与 BCFE关于BC所在直线对称,
∴∠ABC=∠EBC,
∵∠ABE=86°,
∴∠EBC=×86°=43°,
在 BCFE中,∠E=180°﹣∠EBC=180°﹣43°=137°.
故选A.
点评:本题考查了轴对称的性质,平行四边形的性质,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.
练4.【解析】轴对称的性质:
(1)如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
(2)轴对称图形的对称轴也是任何一对对应点所连线段的垂直平分线.
解:∵两个四边形关于直线l对称,
∴四边形ABCD≌四边形FEHG,
∴∠H=∠C=90°,∠A=∠F=80°,∠E=∠B=135°,
∴∠G=360°﹣∠H﹣∠A﹣∠F=55°,
∴a=5cm b=4cm.
点评:主要考查了轴对称的性质和四边形的内角和是360度的实际运用,难度不大.
课后小测答案:
一、选择题
1.【解析】根据圆的性质:沿经过圆心的任何一条直线对折,圆的两部分都能重合,即可得到经过圆心的任何一条直线都是圆的对称轴,据此即可判断.
解:圆的对称轴是经过圆心的直线,有无数条.
故选:D.
2.【解析】根据轴对称的概念:把一 ( http: / / www.21cnjy.com )个图形沿某一条直线折叠,如果它能够与另一个图形重合,称轴对称,及轴对称的含义:①有两个图形,且这两个图形能够完全重合,即形状大小完全相同;②对重合的方式有限制,只能是把它们沿一条直线对折后能够重合,解答即可.
解:A、应该是BC垂直平分AA′,故本选项错误;
B、线段的一条对称轴是它本身所在的直线,故本选项正确;
C、一条线段的一个端点的对称点是另一个端点,故本选项正确;
D、等边三角形是轴对称图形,故本选项正确.
故选A.
点评:本题考查轴对称的概念及性质,属于基础题,掌握基本的概念是解答此类题目的关键.
3.【解析】根据等边三角形,正方形,角,圆的轴对称性,即可作出判断.
解:A、等边三角形的对称轴是各边的中垂线,有3条,故正确;
B、正方形对称轴是边的中垂线与经过相对顶点的直线,共有4条,故选项正确;
C、角的对称轴是角的平分线所在的直线,只有一条,故错误;
D、圆的对称轴是经过圆心的直线,有无数条,故正确.
故选:C.
点评:本题考查生活中的轴对称问题,正确理解常见的几个图形的性质是解题的关键.
4.【解析】根据轴对称的定义,结合所给图形即可作出判断.
解:A、是轴对称图形,故本选项错误;
B、是轴对称图形,故本选项错误;
C、不是轴对称图形,故本选项正确;
D、是轴对称图形,故本选项错误;
故选:C.
点评:此题考查了轴对称的知识,属于基础题,解答本题的关键是熟练掌握轴对称的定义及特点.
5.【解析】根据轴对称图形的概念:关于某条直线对称的图形叫轴对称图形.求解
解:(1)(2)(4)都不是轴对称图形,只有(3)是轴对称图形.
故选:B.
点评:轴对称图形的判断方法:如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形.
6.【解析】根据轴对称图形的概念求解.
解:A、不是轴对称图形,故错误;
B、不是轴对称图形,故错误;
C、是轴对称图形,故正确;
D、不是轴对称图形,故错误.
故选:C.
点评:本题考查了轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合.
7.【解析】根据轴对称图形定义:如 ( http: / / www.21cnjy.com )果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析.
解:①③不是轴对称图形,②④是轴对称图形,因此共有2个轴对称图形,
故选:C.
点评:此题主要考查了轴对称图形,关键是找出图形的对称轴.
8.【解析】先根据△ABC和△A′B′C′关 ( http: / / www.21cnjy.com )于直线l对称得出△ABC≌△A′B′C′,故可得出∠C=∠C′,再由三角形内角和定理即可得出结论.
解:∵△ABC和△A′B′C′关于直线l对称,∠A=50°,∠C′=30°,
∴△ABC≌△A′B′C′,
∴∠C=∠C′=30°,
∴∠B=180°﹣∠A﹣∠C=180°﹣50°﹣30°=100°.
故选:D.
点评:本题考查的是轴对称的性质,熟知关于轴对称的两个图形全等是解答此题的关键.
9.【解析】根据轴对称的性质可得∠D=∠∠B=60°,∠BCA=∠DCA,再根据∠DCA的度数,进而得到答案.
解:根据轴对称的性质可得∠D=∠∠B=60°,
∵∠CAD=60゜,
∴∠DCA=180°﹣60°﹣40°=80°,
根据轴对称的性质可得∠BCA=∠DCA=80°,
∴∠BCD=160°,
故选:A.
点评:此题主要考查了轴对称的性质,关键是掌握轴对称的对应角相等,对应边相等.
10.【解析】根据中心对称,轴对称,平移变换的性质对各选项分析判断即可得解.
解:A、是中心对称图形,故本选项错误;
B、是轴对称图形,故本选项正确;
C、是平移变换图形,故本选项错误;
D、是旋转变换图形,故本选项错误.
故选:B.
点评:本题考查轴对称的性质 ( http: / / www.21cnjy.com ),对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.
11.【解析】分别根据轴对称的性质、角平分线及圆的性质对各选项进行逐一判断即可.
解:A、到直线l的距离相等的两点不一定关于直线l对称,故本选项错误;
B、角的两边关于角平分线所在的直线对称,故本选项错误;
C、圆是轴对称图形,有无数条对称轴,故本选项正确;
D、有一个内角为60°的等腰三角形是轴对称图形,故本选项错误.
故选:C.
点评:本题考查的是轴对称的性质,熟知如果两个图形的对应点的连线被同一条直线垂直平分,那么这两个图形关于这条直线对称是解答此题的关键.
12.【解析】利用轴对称图形的性质得出对应角,进而得出答案.
解;∵△ABC关于直线a对称,
∴∠E=∠B,∠D=∠A,∠F=∠C,
则∠F的度数是:30°.
故选:A.
点评:此题主要考查了轴对称图形的性质,得出对应角是解题关键.
二、填空题
13.【解析】认真观察所给的图形,按照直线两旁的部分是否能够互相重合来判断是否符合要求.
解:3中的伞把不对称,故填①②④
故填①②④
点评:本题考查了生活中的轴对称问题;轴对称的关键是寻找对称轴,观察直线两边图象折叠后可重合是正确解答本题的关键.
14.【解析】先得到数字“5”的轴对称图形,根据图形即可求解.
解:根据轴对称图形的定义可知,数字“5”的轴对称图形是数字2.
故答案为:2.
点评:考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
15.【解析】关于某条直线对称的图形叫轴对称图形.
解:第1,2,4个图形沿某条直线折叠后直线两旁的部分能够完全重合,是轴对称图形,故填3.
点评:轴对称的关键是寻找对称轴,两边图象折叠后可重合.
16.【解析】根据已知得出是连续的偶数且每两个数组成轴对称图形进而得出答案.
解:由题意得出:
数据是连续的偶数且每两个数组成轴对称图形,故空格处应该是.
故答案为:.
点评:此题主要考查了轴对称图形的性质,根据题意得出数组变化规律是解题关键.
17.【解析】根据轴对称图形的概念,分析各图形的对称轴条数求解.
解:线段有两条对称轴:是它的中垂线和它自身所在的直线;
角有一条对称轴:是角平分线所在的直线;
长方形有两条对称轴:分别是两组对边的中垂线;
等腰梯形有一条对称轴:是上底和下底的中垂线.
故填:线段、长方形.
点评:掌握轴对称图形的概念.轴对称图形的关键是寻找对称轴,注意不要遗漏.
三、解答题
18.【解析】仔细观察会发现它们都是轴对称图形,所以在空白处再画一个轴对称图形即可.
解:从图中可以发现所有的图形都是轴对称图形,而且图形从左到右分别是1﹣7的数字,
所以画一个轴对称图形且数字为6即可.
所填图形为:.
点评:本题是一道规律型的题,首先要从图中找出规律,然后再根据规律画图.但还是考查了轴对称图形的性质.
加拿大 澳大利亚 乌拉圭 瑞典 瑞士
二、知识回顾 1.如图(1),OC平分∠AOB,则∠AOC= ∠BOC = ∠AOB . ( http: / / www.21cnjy.com )2.如图(2),△ABD≌△ACD,AB与AC是对应边.写出这两个三角形的对应顶点和对应边. ( http: / / www.21cnjy.com )对应顶点: A与A;B与C;D与D. 对应边: AD与AD;BD与CD.
三、新知讲解 1.轴对称图形如果一个图形沿一条直线折叠,直线两旁的部分能够 互相重合 ,这个图形就叫做 轴对称图形 ,这条直线就是它的 对称轴 .2.成轴对称的两个图形把一个图形沿着某一条直线 折叠 ,如 ( http: / / www.21cnjy.com )果它能够与另一个图形 重合 ,那么就说这两个图形关于这条直线(成轴)对称,这条直线叫做 对称轴 ,折叠后重合的点是对应点,叫做 对称点 .3.轴对称图形与成轴对称的两个图形的区别与联系:区别一个具有特殊形状的图形,至少有一条对称轴.两个图形的位置关系,只有一条对称轴.联系如果把轴对称图形沿对称轴分成两部分,那么这两部分就是这条直线成轴对称.如果把两个成轴对称的图形拼在一起,看成一个整体,那么它就是一个轴对称图形.4.线段的垂直平分线经过线段中点并且垂直这条线段的直线,叫做这条线段的 垂直平分线 .5.轴对称的性质:(1)成轴对称的两个图形全等.(2)如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连接线段的垂直平分线.类似地,轴对称图形的对称轴,是任何一对对应点所连接线段的垂直平分线.(3)两个图形关于某条直线对称,如果他们的对应线段或其延长线相交,那么交点一定在对称轴上.
四、典例探究 扫一扫,有惊喜哦!1.轴对称几何图形的识别【例1】(2015 乐陵市模拟)如图,图中的图形是常见的安全标记,其中是轴对称图形的是()A. ( http: / / www.21cnjy.com ) B. C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )总结:判断一个图形是轴对称图形的关键是寻找到对称 ( http: / / www.21cnjy.com )轴. 如果有一条直线,使得图形两部分折叠后可重合,那么这个图形就是轴对称图形,这条直线就是对称轴.几何图形中的线段、角、正方形、长方形、等腰三角形、等腰梯形、圆等都是轴对称图形.练1.如图,国旗是一个国家的象征,观察下面的国旗,是轴对称图形的是().A.加拿大、澳大利亚、乌拉圭 B.加拿大、澳大利亚、瑞典C.加拿大、瑞典、瑞士 D.乌拉圭、瑞典、瑞士2.识别成轴对称的两个图形【例2】下面给出的每组照片中的两个图案成轴对称吗?如果是,试着找出它们的对称轴,并找出一对对称点. ( http: / / www.21cnjy.com )总结:成轴对称的两个图形可以沿着某一条直线折叠后能重合,这条直线是对称轴.成轴对称和轴对称图形是两个不同的概念,两者既有联系又有区别.练2.在下列选项中,右边图形与左边图形成轴对称的是( ). ( http: / / www.21cnjy.com )3.根据成轴对称的两个图形的特征进行判断【例3】(2013秋 盐都区期末)如图是一 ( http: / / www.21cnjy.com )个风筝设计图,其主体部分(四边形ABCD)关于BD所在的直线对称,AC与BD相交于点O,且AB≠AD,则下列判断不正确的是( ) ( http: / / www.21cnjy.com )A.△ABD≌△CBD B.△ABC是等边三角形C.△AOB≌△COB D.△AOD≌△COD总结:如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.成轴对称的两个图形全等.练3.(2014 柳州)如图,直角坐标系中的五角星关于y轴对称的图形在( ) ( http: / / www.21cnjy.com )A.第一象限 B.第二象限 C.第三象限 D.第四象限4.根据成轴对称的两个图形的特征进行求解【例4】(2015 温州一模)如图,若 ABCD与 BCFE关于BC所在直线对称,∠ABE=86°,则∠E等于( ) ( http: / / www.21cnjy.com )A.137° B.104° C.94° D.86°总结:成轴对称的两个图形的对应边相等、对应角相等.对称轴上的任何一点到两个对应点之间的距离相等.练4.(2014秋 扶余县期中)如图,两个四边形关于直线l对称,∠C=90°,试写出a,b的长度,并求出∠G的度数. ( http: / / www.21cnjy.com )
五、课后小测 一、选择题1.(2013秋 仪征市校级期末)圆是轴对称图形,它的对称轴有()A.1条 B.2条 C.3条 D.无数条2.下列说法错误的是()A.若A,A′是以BC为轴对称的点,则AA′垂直平分BCB.线段的一条对称轴是它本身所在的直线C.一条线段的一个端点的对称点是另一个端点D.等边三角形是轴对称图形3.下列说法错误的是()A.等边三角形有3条对称轴 B.正方形有4条对称轴C.角的对称轴有2条 D.圆有无数条对称轴4.(2015 潍坊模拟)下列图形中,不是轴对称图形的是()A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )5.(2015 伊春模拟)下列体育运动标志中,从图案看不是轴对称图形的有()个. ( http: / / www.21cnjy.com )A.4 B.3 C.2 D.16.(2015 杭州模拟)下面四幅画分别是体育运动长鼓舞,武术,举重、摔跤抽象出来的简笔画,其中是轴对称图形的是()A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )7.(2015 南开区一模)下列四个图形中,轴对称图形有() ( http: / / www.21cnjy.com )A.4个 B.3个 C.2个 D.1个8.(2014秋 厦门期末)如图,△ABC和△A′B′C′关于直线l对称,若∠A=50°,∠C′=30°,则∠B的度数为() ( http: / / www.21cnjy.com )A.30° B.50° C.90° D.100°9.(2014秋 孝南区期末)如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠B=40゜,∠CAD=60゜,则∠BCD=() ( http: / / www.21cnjy.com )A.160゜ B.120゜ C.80゜ D.100゜10.(2014秋 石家庄期末)下列图形中,△A′B′C′与△ABC成轴对称的是()A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )11.(2014春 环翠区校级期末)下列说法中,正确的是()A.到直线l的距离相等的两点关于直线l对称B.角的两边关于角的平分线对称C.圆是轴对称图形,有无数条对称轴D.有一个内角为60°的三角形是轴对称图形12.(2014春 宜宾校级期末)如图,△ABC关于直线a对称,则∠F的度数是() ( http: / / www.21cnjy.com )A.30° B.50° C.90° D.100°二、填空题13.观察下图中各组图形,其中成轴对称的为___________(只写序号1,2等). ( http: / / www.21cnjy.com )14.(2013 上海模拟 ( http: / / www.21cnjy.com ))如图,AB左边是计算器上的数字“5”,若以直线AB为对称轴,那么它的轴对称图形是数字________________. ( http: / / www.21cnjy.com )15.(2010春 海曙区期末)下列图形中,轴对称图形有__________个.16.(2010秋 景洪市校级期末)如图所示,观察规律并填空:空格处应该是_______.17.(2009秋 南京期中)线段、角、平行四边形、长方形、等腰梯形中有两条对称轴的是_____.三、解答题18.(2013秋 赣县校级期中)如图,在下面一组图形符号中找出它们所蕴含的内在规律,然后在横线上的空白处填上恰当的图形. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】根据轴对称图形的概念: ( http: / / www.21cnjy.com )如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形.据此对常见的安全标记图形进行判断.
解:A、有一条对称轴,是轴对称图形,符合题意;
B、不是轴对称图形,因为找不到任何一条直线,使它沿这条直线折叠后,直线两旁的部分能够重合,即不满足轴对称图形的定义.不符合题意;
C、不是轴对称图形,因为找不到任何一条直线,使它沿这条直线折叠后,直线两旁的部分能够重合,即不满足轴对称图形的定义.不符合题意;
D、不是轴对称图形,因为找不到任何一条直线,使它沿这条直线折叠后,直线两旁的部分能够重合,即不满足轴对称图形的定义.不符合题意.
故选A.
练1.【解析】根据轴对称图形的定义,加拿大、瑞典、瑞士的国旗是轴对称图形,故选C.
【例2】【解析】甲组是两幅相同的图案,但不成轴对称;
乙组的两个图形,把其中的一个图形折叠后可以与另一个图形重合,那么这个两个图案成轴对称,其对称轴如图所示;
( http: / / www.21cnjy.com )
丙组的两个图案不成轴对称.
练2.【解析】C的两个图形沿线折叠后重合,根据成轴对称的两个图形的定义,故选C.
【例3】【解析】先根据轴对称的性质得出AB=BC,AD=CD,OA=OC,BD⊥AC,再根据全等三角形的判定定理即可得出结论.
解:∵主体部分(四边形ABCD)关于BD所在的直线对称,AC与BD相交于点O,
∴AB=BC,AD=CD,OA=OC,BD⊥AC,
在△ABD与△CBD中,
,
∴△ABD与△CBD,故A正确;
在△AOB与△COB中,
∴△AOB≌△COB,故C正确;
在△AOD与△COD中,
,
∴△AOD≌△COD,故D正确;
△ABC是等腰三角形,故B错误.
故选:B.
点评:本题考查的是轴对称的性质,熟知如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线是解答此题的关键.
练3.【解析】根据轴对称的性质作出选择.
解:如图所示,直角坐标系中的五角星关于y轴对称的图形在第一象限.
故选:A.
( http: / / www.21cnjy.com )
点评:本题考查了轴对称的性质.此题难度不大,采用了“数形结合”的数学思想.
【例4】【解析】根据轴对称的性质可得∠ABC=∠EBC,然后求出∠EBC,再根据平行四边形邻角互补列式计算即可得解.
解:∵ ABCD与 BCFE关于BC所在直线对称,
∴∠ABC=∠EBC,
∵∠ABE=86°,
∴∠EBC=×86°=43°,
在 BCFE中,∠E=180°﹣∠EBC=180°﹣43°=137°.
故选A.
点评:本题考查了轴对称的性质,平行四边形的性质,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.
练4.【解析】轴对称的性质:
(1)如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
(2)轴对称图形的对称轴也是任何一对对应点所连线段的垂直平分线.
解:∵两个四边形关于直线l对称,
∴四边形ABCD≌四边形FEHG,
∴∠H=∠C=90°,∠A=∠F=80°,∠E=∠B=135°,
∴∠G=360°﹣∠H﹣∠A﹣∠F=55°,
∴a=5cm b=4cm.
点评:主要考查了轴对称的性质和四边形的内角和是360度的实际运用,难度不大.
课后小测答案:
一、选择题
1.【解析】根据圆的性质:沿经过圆心的任何一条直线对折,圆的两部分都能重合,即可得到经过圆心的任何一条直线都是圆的对称轴,据此即可判断.
解:圆的对称轴是经过圆心的直线,有无数条.
故选:D.
2.【解析】根据轴对称的概念:把一 ( http: / / www.21cnjy.com )个图形沿某一条直线折叠,如果它能够与另一个图形重合,称轴对称,及轴对称的含义:①有两个图形,且这两个图形能够完全重合,即形状大小完全相同;②对重合的方式有限制,只能是把它们沿一条直线对折后能够重合,解答即可.
解:A、应该是BC垂直平分AA′,故本选项错误;
B、线段的一条对称轴是它本身所在的直线,故本选项正确;
C、一条线段的一个端点的对称点是另一个端点,故本选项正确;
D、等边三角形是轴对称图形,故本选项正确.
故选A.
点评:本题考查轴对称的概念及性质,属于基础题,掌握基本的概念是解答此类题目的关键.
3.【解析】根据等边三角形,正方形,角,圆的轴对称性,即可作出判断.
解:A、等边三角形的对称轴是各边的中垂线,有3条,故正确;
B、正方形对称轴是边的中垂线与经过相对顶点的直线,共有4条,故选项正确;
C、角的对称轴是角的平分线所在的直线,只有一条,故错误;
D、圆的对称轴是经过圆心的直线,有无数条,故正确.
故选:C.
点评:本题考查生活中的轴对称问题,正确理解常见的几个图形的性质是解题的关键.
4.【解析】根据轴对称的定义,结合所给图形即可作出判断.
解:A、是轴对称图形,故本选项错误;
B、是轴对称图形,故本选项错误;
C、不是轴对称图形,故本选项正确;
D、是轴对称图形,故本选项错误;
故选:C.
点评:此题考查了轴对称的知识,属于基础题,解答本题的关键是熟练掌握轴对称的定义及特点.
5.【解析】根据轴对称图形的概念:关于某条直线对称的图形叫轴对称图形.求解
解:(1)(2)(4)都不是轴对称图形,只有(3)是轴对称图形.
故选:B.
点评:轴对称图形的判断方法:如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形.
6.【解析】根据轴对称图形的概念求解.
解:A、不是轴对称图形,故错误;
B、不是轴对称图形,故错误;
C、是轴对称图形,故正确;
D、不是轴对称图形,故错误.
故选:C.
点评:本题考查了轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合.
7.【解析】根据轴对称图形定义:如 ( http: / / www.21cnjy.com )果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析.
解:①③不是轴对称图形,②④是轴对称图形,因此共有2个轴对称图形,
故选:C.
点评:此题主要考查了轴对称图形,关键是找出图形的对称轴.
8.【解析】先根据△ABC和△A′B′C′关 ( http: / / www.21cnjy.com )于直线l对称得出△ABC≌△A′B′C′,故可得出∠C=∠C′,再由三角形内角和定理即可得出结论.
解:∵△ABC和△A′B′C′关于直线l对称,∠A=50°,∠C′=30°,
∴△ABC≌△A′B′C′,
∴∠C=∠C′=30°,
∴∠B=180°﹣∠A﹣∠C=180°﹣50°﹣30°=100°.
故选:D.
点评:本题考查的是轴对称的性质,熟知关于轴对称的两个图形全等是解答此题的关键.
9.【解析】根据轴对称的性质可得∠D=∠∠B=60°,∠BCA=∠DCA,再根据∠DCA的度数,进而得到答案.
解:根据轴对称的性质可得∠D=∠∠B=60°,
∵∠CAD=60゜,
∴∠DCA=180°﹣60°﹣40°=80°,
根据轴对称的性质可得∠BCA=∠DCA=80°,
∴∠BCD=160°,
故选:A.
点评:此题主要考查了轴对称的性质,关键是掌握轴对称的对应角相等,对应边相等.
10.【解析】根据中心对称,轴对称,平移变换的性质对各选项分析判断即可得解.
解:A、是中心对称图形,故本选项错误;
B、是轴对称图形,故本选项正确;
C、是平移变换图形,故本选项错误;
D、是旋转变换图形,故本选项错误.
故选:B.
点评:本题考查轴对称的性质 ( http: / / www.21cnjy.com ),对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.
11.【解析】分别根据轴对称的性质、角平分线及圆的性质对各选项进行逐一判断即可.
解:A、到直线l的距离相等的两点不一定关于直线l对称,故本选项错误;
B、角的两边关于角平分线所在的直线对称,故本选项错误;
C、圆是轴对称图形,有无数条对称轴,故本选项正确;
D、有一个内角为60°的等腰三角形是轴对称图形,故本选项错误.
故选:C.
点评:本题考查的是轴对称的性质,熟知如果两个图形的对应点的连线被同一条直线垂直平分,那么这两个图形关于这条直线对称是解答此题的关键.
12.【解析】利用轴对称图形的性质得出对应角,进而得出答案.
解;∵△ABC关于直线a对称,
∴∠E=∠B,∠D=∠A,∠F=∠C,
则∠F的度数是:30°.
故选:A.
点评:此题主要考查了轴对称图形的性质,得出对应角是解题关键.
二、填空题
13.【解析】认真观察所给的图形,按照直线两旁的部分是否能够互相重合来判断是否符合要求.
解:3中的伞把不对称,故填①②④
故填①②④
点评:本题考查了生活中的轴对称问题;轴对称的关键是寻找对称轴,观察直线两边图象折叠后可重合是正确解答本题的关键.
14.【解析】先得到数字“5”的轴对称图形,根据图形即可求解.
解:根据轴对称图形的定义可知,数字“5”的轴对称图形是数字2.
故答案为:2.
点评:考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
15.【解析】关于某条直线对称的图形叫轴对称图形.
解:第1,2,4个图形沿某条直线折叠后直线两旁的部分能够完全重合,是轴对称图形,故填3.
点评:轴对称的关键是寻找对称轴,两边图象折叠后可重合.
16.【解析】根据已知得出是连续的偶数且每两个数组成轴对称图形进而得出答案.
解:由题意得出:
数据是连续的偶数且每两个数组成轴对称图形,故空格处应该是.
故答案为:.
点评:此题主要考查了轴对称图形的性质,根据题意得出数组变化规律是解题关键.
17.【解析】根据轴对称图形的概念,分析各图形的对称轴条数求解.
解:线段有两条对称轴:是它的中垂线和它自身所在的直线;
角有一条对称轴:是角平分线所在的直线;
长方形有两条对称轴:分别是两组对边的中垂线;
等腰梯形有一条对称轴:是上底和下底的中垂线.
故填:线段、长方形.
点评:掌握轴对称图形的概念.轴对称图形的关键是寻找对称轴,注意不要遗漏.
三、解答题
18.【解析】仔细观察会发现它们都是轴对称图形,所以在空白处再画一个轴对称图形即可.
解:从图中可以发现所有的图形都是轴对称图形,而且图形从左到右分别是1﹣7的数字,
所以画一个轴对称图形且数字为6即可.
所填图形为:.
点评:本题是一道规律型的题,首先要从图中找出规律,然后再根据规律画图.但还是考查了轴对称图形的性质.
加拿大 澳大利亚 乌拉圭 瑞典 瑞士
