【多媒体导学案】人教版数学八年级上册第十三章第10课时 含30°角的直角三角形(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学八年级上册第十三章第10课时 含30°角的直角三角形(教师版) |

|
|
| 格式 | zip | ||
| 文件大小 | 180.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-10 10:49:25 | ||
图片预览


文档简介
一、学习目标 探索并掌握含30°角直角三角形的性质;会应用该性质进行相关的证明和计算.
二、知识回顾 一、等边三角形的性质1.等边三角形的三条边相等;2.等边三角形的三个内角都相等,且都等于60°;3.等边三角形是轴对称图形,有三条对称轴;4.等边三角形每条边上的中线、高线和所对角的平分线都相互重合.二、等边三角形的判定1.三边相等的三角形是等边三角形;2.三个角都相等的三角形是等边三角形;3.有一个内角等于60°的等腰三角形是等边三角形.
三、新知讲解 含30°角的直角三角形的性质性质:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.几何语言:∵在Rt△ABC中,∠C=90°,∠A=30°,∴BC=AB. ( http: / / www.21cnjy.com )
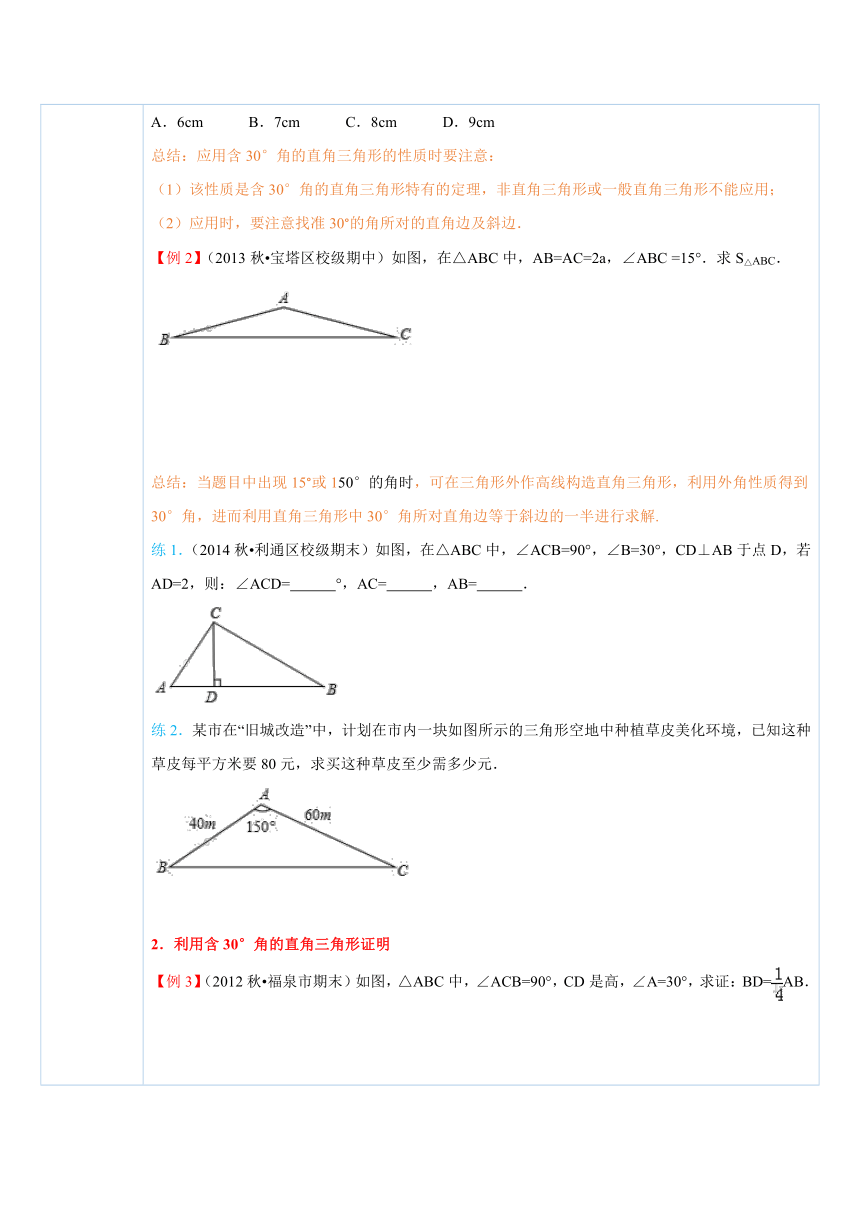
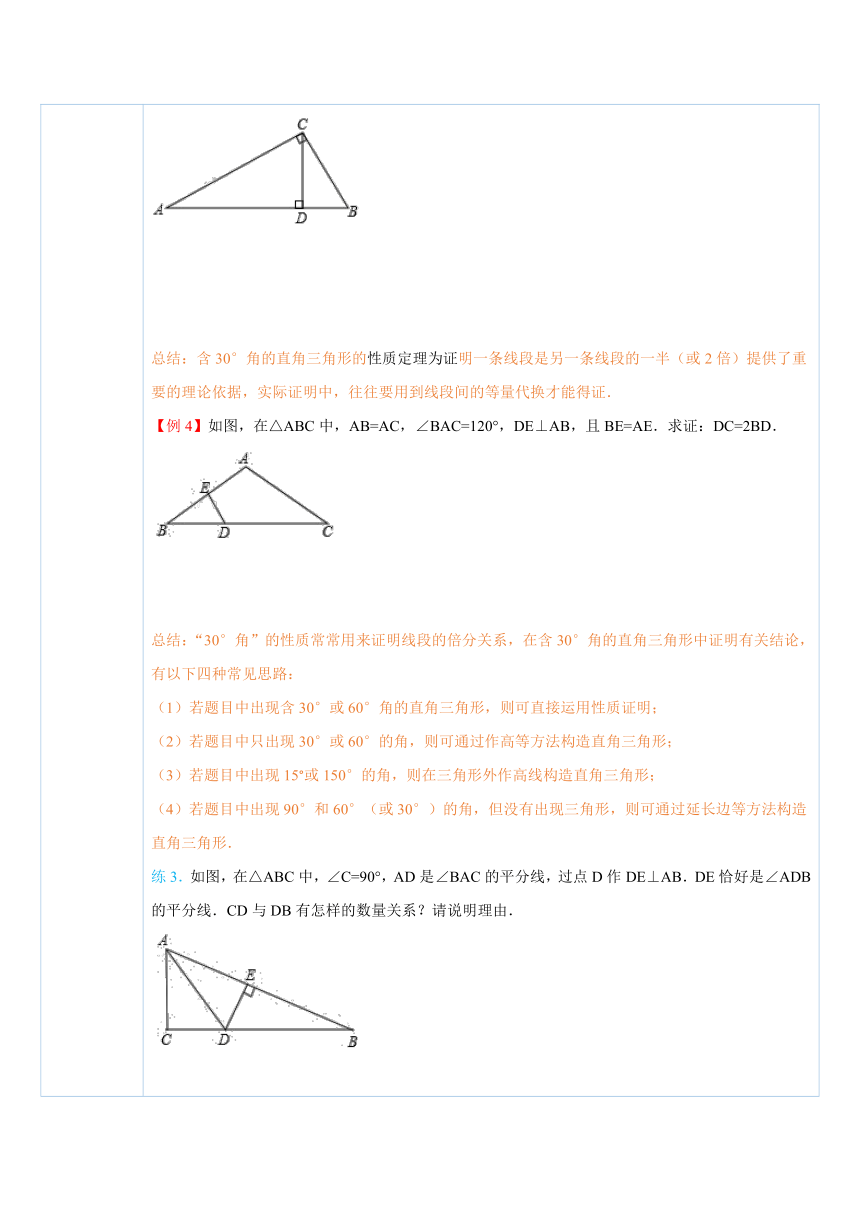
四、典例探究 扫一扫,有惊喜哦!1.利用含30°角的直角三角形的性质求解【例1】(2014秋 乳山市期中)如图,在Rt△ABC中,∠C=90°,∠A=30°,AB+BC=12cm,则AB等于( ) ( http: / / www.21cnjy.com )A.6cm B.7cm C.8cm D.9cm总结:应用含30°角的直角三角形的性质时要注意:(1)该性质是含30°角的直角三角形特有的定理,非直角三角形或一般直角三角形不能应用;(2)应用时,要注意找准30°的角所对的直角边及斜边.【例2】(2013秋 宝塔区校级期中)如图,在△ABC中,AB=AC=2a,∠ABC =15°.求S△ABC. ( http: / / www.21cnjy.com )总结:当题目中出现15°或150°的角时 ( http: / / www.21cnjy.com ),可在三角形外作高线构造直角三角形,利用外角性质得到30°角,进而利用直角三角形中30°角所对直角边等于斜边的一半进行求解.练1.(2014秋 利通区校级期末)如图, ( http: / / www.21cnjy.com )在△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于点D,若AD=2,则:∠ACD= °,AC= ,AB= . ( http: / / www.21cnjy.com )练2.某市在“旧城改造”中,计划在市内一块如图所示的三角形空地中种植草皮美化环境,已知这种草皮每平方米要80元,求买这种草皮至少需多少元. ( http: / / www.21cnjy.com )2.利用含30°角的直角三角形证明【例3】(2012秋 福泉市期末)如图,△ABC中,∠ACB=90°,CD是高,∠A=30°,求证:BD=AB. ( http: / / www.21cnjy.com )总结:含30°角的直角三角形的性质定理为证 ( http: / / www.21cnjy.com )明一条线段是另一条线段的一半(或2倍)提供了重要的理论依据,实际证明中,往往要用到线段间的等量代换才能得证.【例4】如图,在△ABC中,AB=AC,∠BAC=120°,DE⊥AB,且BE=AE.求证:DC=2BD. ( http: / / www.21cnjy.com )总结:“30°角”的性质常常用来证明线段的倍分关系,在含30°角的直角三角形中证明有关结论,有以下四种常见思路:(1)若题目中出现含30°或60°角的直角三角形,则可直接运用性质证明;(2)若题目中只出现30°或60°的角,则可通过作高等方法构造直角三角形;(3)若题目中出现15°或150°的角,则在三角形外作高线构造直角三角形;(4)若题目中出现90°和60°(或30°)的角,但没有出现三角形,则可通过延长边等方法构造直角三角形.练3.如图,在△ABC中, ( http: / / www.21cnjy.com )∠C=90°,AD是∠BAC的平分线,过点D作DE⊥AB.DE恰好是∠ADB的平分线.CD与DB有怎样的数量关系?请说明理由. ( http: / / www.21cnjy.com )练4.(2011秋 庐阳区期末)如图: ( http: / / www.21cnjy.com )△ABC中,∠B=60°,AB=10,BC=6,D为BC上一点,且BD=2DC,连接AD.求证:AD=AC. ( http: / / www.21cnjy.com )
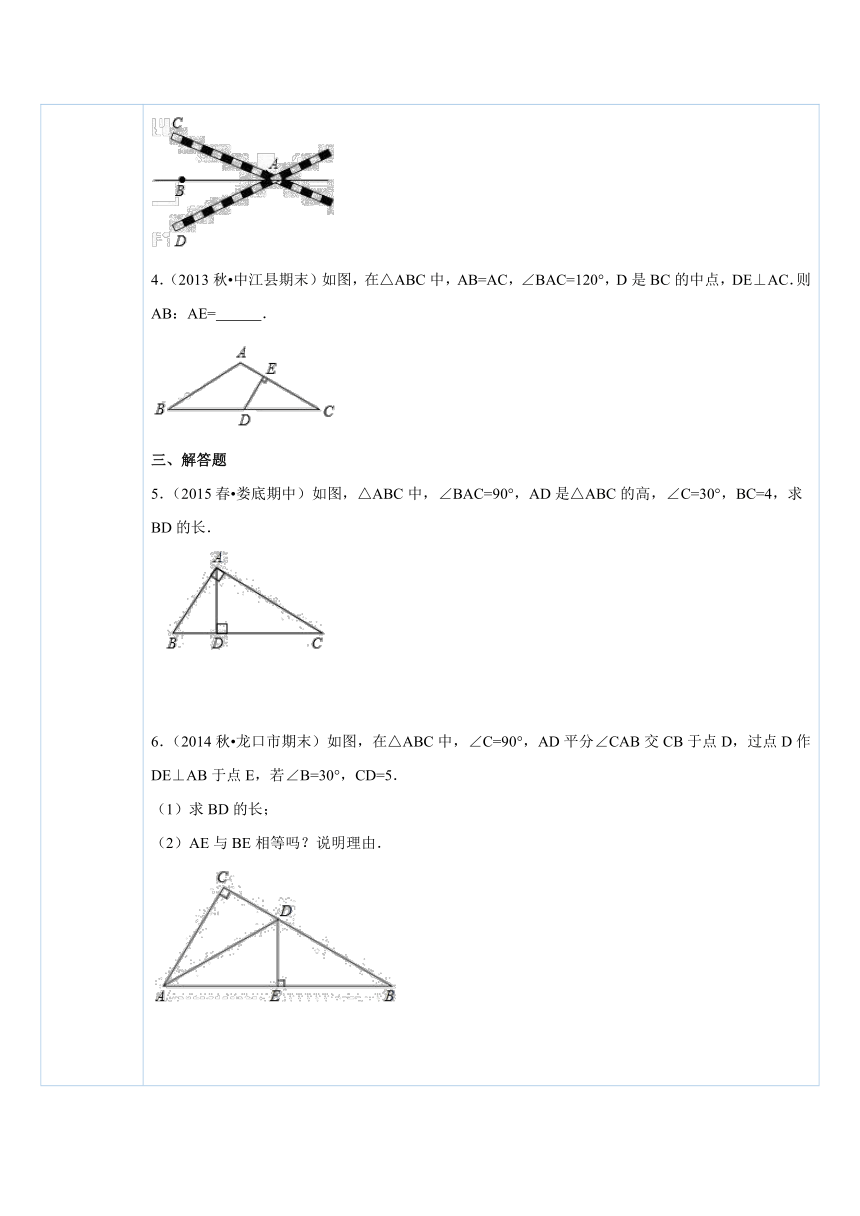
五、课后小测 一、选择题1.(2013秋 建阳市期末)如图 ( http: / / www.21cnjy.com ),在Rt△ABC中,∠C=90°,∠B=30°,CD是斜边AB上的高,AD=3cm,则AB的长度是( ) ( http: / / www.21cnjy.com )A.3cm B.6cm C.9cm D.12cm2.(2015 宜城市模拟)如图, ( http: / / www.21cnjy.com )已知∠AOB=60°,点P在边OA上,OP=8,点M,N在边OB上,PM=PN,若MN=2,则ON=( ) ( http: / / www.21cnjy.com )A.6 B.5 C.4 D.3二、填空题3.(2013秋 新浦区校级月考)如图,铁路 ( http: / / www.21cnjy.com )AC与铁路AD相交于车站A,B区在∠CAD的平分线上,且距车站A为20千米,∠DAC=60°,则B区距铁路AC的距离为 千米. ( http: / / www.21cnjy.com )4.(2013秋 中江县期末)如图,在△ABC中,AB=AC,∠BAC=120°,D是BC的中点,DE⊥AC.则AB:AE= . ( http: / / www.21cnjy.com )三、解答题5.(2015春 娄底期中)如图,△ABC中,∠BAC=90°,AD是△ABC的高,∠C=30°,BC=4,求BD的长. ( http: / / www.21cnjy.com )6.(2014秋 龙口市期 ( http: / / www.21cnjy.com )末)如图,在△ABC中,∠C=90°,AD平分∠CAB交CB于点D,过点D作DE⊥AB于点E,若∠B=30°,CD=5.(1)求BD的长;(2)AE与BE相等吗?说明理由. ( http: / / www.21cnjy.com )7.(2014秋 五常市校级期中)如图,△ABC中,AB=AC,∠BAC=120°,AD⊥AC交BC于点D,求证:BC=3AD. ( http: / / www.21cnjy.com )8.(2013春 修水县校级期末)如图,在△ABC中,AB=AC=8cm,∠A=30°,求△ABC的面积. ( http: / / www.21cnjy.com )9.(2011 永嘉县校级自主招生)如图,在△ABC中,AD交边BC于点D,∠BAD=15°,∠ADC=4∠BAD,DC=2BD.(1)求∠B的度数;(2)求证:∠CAD=∠B. ( http: / / www.21cnjy.com )10.(2009 河北模拟)在四边形ABCD中,对角线AC平分∠DAB,∠DAB=120°,∠B=∠D=90°,求证:AB+AD=AC. ( http: / / www.21cnjy.com )11.(2008秋 莒南 ( http: / / www.21cnjy.com )县月考)如图,已知某船于上午8点在A处观测小岛C在北偏东60°方向上.该船以每小时40海里的速度向东航行到B处,此时测得小岛C在北偏东30°方向上.船以原速度再继续向东航行2小时到达小岛C的正南方D点.求船从A到D一共走了多少海里? ( http: / / www.21cnjy.com )12.如图,在△ABC中,AB=AC,D是BC边上的中点,DE⊥AB,DF⊥AC,垂足为E,F,∠BAC=120°,求证:DE+DF=BC. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】根据含30°角的直角三角形的性质,易知AB=2BC,联立AB+BC=12cm,即可求得AB、BC的长.
解:Rt△ABC中,∠C=90°,∠A=30°,
∴AB=2BC.
∴AB+BC=3BC=12cm,即BC=4cm,AB=2BC=8cm.
故选C.
点评:此题考查的是直角三角形中30°角的性质:在直角三角形中,30°角所对直角边等于斜边的一半.
【例2】【解析】如图,延长BA,过点C作CD⊥AD,则根据“等腰△ABC的两个底角相等”及三角形外角性质推知∠DAC=30°.由“30度角所对的直角边等于斜边的一半”得到CD=AC=a.最后由三角形的面积公式来解题.
解:如图,延长BA,过点C作CD⊥AD,
( http: / / www.21cnjy.com )
∵AB=AC
∴∠ABC=∠ACB=15°,
∵∠DAC是△ABC的外角,
∴∠DAC=30°,
∴CD=AC=a,
∴S△ABC=AB CD=×2a×a=a2.
点评:本题考查了含30度角的直角三角形的性质,等腰三角形的性质.应用时,要注意找准30°的角所对的直角边与斜边.
练1.【解析】根据同角的余角相等可得出∠ACD=∠B,可得到AC长,在直角三角形BCA中,可得出AB.
解:∵∠ACB=90°,
∴∠ACD+∠BCD=90°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠ACD+∠A=90°,
∴∠ACD=∠B=30°,
∵AD=2,
∴AC=4,
在△ABC中,∠ACB=90°,∠B=30°,
∴AB=2AC=8,
故答案为:30;4;8.
点评:本题考查了含30°角的直角三角形的性质,30°所对的直角边等于斜边的一半.是基础知识要熟练掌握.
练2.【解析】作BA边的高CD,设与B ( http: / / www.21cnjy.com )A的延长线交于点D,则∠DAC=30°,由AC=60m,即可求出CD=30m,然后根据三角形的面积公式即可推出△ABC的面积为600m2,最后根据每平方米的售价即可推出结果.
解:如图,作BA边的高CD,设与BA的延长线交于点D,
( http: / / www.21cnjy.com )
∵∠BAC=150°,
∴∠DAC=30°,
∵CD⊥BD,AC=60m,
∴CD=30m,
∵AB=40m,
∴S△ABC=AB×CD=×40×30=600m2,
∵每平方米售价80元,
∴购买这种草皮的价格为600×80=48000元.
答:买这种草皮至少需48000元.
点评:本题主要考查三角形的面积公式,含 ( http: / / www.21cnjy.com )30度角的直角三角形的性质,关键在于做出AB边上的高,根据相关的性质推出高CD的长度,正确的计算出△ABC的面积.
【例3】【解析】根据直角三角形30°角所对的直角边等于斜边的一半的性质求出BC=AB,再求出∠BCD=30°,再次利用此性质解答即可得证.
证明:∵∠ACB=90°,∠A=30°,
∴BC=AB,(直角三角形中,30°所对直角边等于斜边的一半),
∵CD是高,
∴∠ADC=90°,
∴∠ACD=60°,
∴∠BCD=30°,
∴BD=BC,
∴BD=AB.
点评:本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质,两次利用性质是解题的关键.
【例4】【解析】连接AD.在△ABC中,根据等边对等角的性质及三角形内角和定理求出∠B=∠C=(180°﹣∠BAC)=30°.由DE是AB的垂直平分线得出AD=BD,那么∠BAD=∠B=30°,那么∠DAC=∠BAC﹣∠BAD=90°.然后在Rt△ADC中,根据30°角所对的直角边等于斜边的一半,得出DC=2AD,等量代换即可得到DC=2BD.
证明:连接AD.
( http: / / www.21cnjy.com )
∵在△ABC中,AB=AC,∠BAC=120°,
∴∠B=∠C=(180°﹣∠BAC)=30°.
∵DE⊥AB,BE=AE,
∴AD=BD.
∴∠BAD=∠B=30°.
∴∠DAC=∠BAC﹣∠BAD=120°﹣30°=90°.
∵在Rt△ADC中,∠DAC=90°,∠C=30°,
∴DC=2AD,
∴DC=2BD.
点评:本题考查了含30度角的直角三 ( http: / / www.21cnjy.com )角形的性质,等腰三角形的性质,三角形内角和定理,垂直平分线的性质,难度适中,熟记并灵活应用各性质是解题的关键.
练3.【解析】由条件先证△AED≌△BED,得出∠BAD=∠CAD=∠B,再根据直角三角形两锐角的和为90°,求得∠B=30°,即可得到CD=DB.
解:CD=DB.理由如下:
∵DE⊥AB,
∴∠AED=∠BED=90°,
∵DE是∠ADB的平分线,
∴∠ADE=∠BDE,
又∵DE=DE,
∴△AED≌△BED(ASA),
∴AD=BD,∠DAE=∠B,
∵∠BAD=∠CAD=∠BAC,
∴∠BAD=∠CAD=∠B,
∵AD=BD,∠BAD+∠CAD+∠B=90°,
∴∠B=∠BAD=∠CAD=30°,
在直角三角形ACD中,∠CAD=30°,
∴CD=AD=BD,
即CD=DB.
点评:本题考查了含30度角的直角三角形的 ( http: / / www.21cnjy.com )性质:在直角三角形中,30°角所对的直角边等于斜边的一半.也考查了全等三角形的判定和性质,直角三角形两锐角和为90°的性质.
练4.【解析】先过A作BC的垂线,交 ( http: / / www.21cnjy.com )BC于E,在直角三角形ABE中,利用30°角所对的边等于斜边的一半,可求BE的长,再根据已知,利用线段的和差可得E是CD的中点,从而证得△ACD是等腰三角形,即AC=AD.
证明:过A作BC的垂线,交BC于E.
( http: / / www.21cnjy.com )
∵∠B=60°,
∴∠BAE=30°,
∴BE=AB=10×=5.
∵BC=6且BD=2DC,
∴BD=4,CD=2,
∴E是CD的中点,
∴E既为垂足又为中点,
∴△ACD是等腰三角形,
∴AC=AD.
点评:本题考查了含30°角的直角三角形的性质和等腰三角形的判定,也可以运用三角函数的知识进行解答.
课后小测答案:
一、选择题
1.【解析】在Rt△ABC中,
( http: / / www.21cnjy.com )
∵CD是斜边AB上的高,
∴∠ADC=90°,
∴∠ACD=∠B=30°(同角的余角相等),
∵AD=3cm,
在Rt△ACD中,AC=2AD=6cm,
在Rt△ABC中,AB=2AC=12cm.
∴AB的长度是12cm.
故选D.
2.【解析】过P作PD⊥OB于点D,
( http: / / www.21cnjy.com )
在Rt△OPD中,∵∠ODP=90°,∠POD=60°,
∴∠OPD=30°,
∴OD=OP=×8=4,
∵PM=PN,PD⊥MN,MN=2,
∴MD=ND=MN=1,
∴ON=OD+DN=4+1=5.
故选:B.
二、填空题
3.【解析】过点B作BE⊥AC于点E,
在Rt△BAE中,BA=20,∠BAE=30°,
所以BE=AB=10.
故应填10.
( http: / / www.21cnjy.com )
4.【解析】如图,连接AD,
( http: / / www.21cnjy.com )
∵AB=AC,D是BC的中点,
∴AD⊥BC,
∵∠BAC=120°,AB=AC,
∴∠C=(180°﹣120°)=30°,
∵DE⊥AC,
∴∠ADE=∠C=30°,
在Rt△ADE中,AD=2AE,
在Rt△ACD中,AC=2AD=4AE,
∵AB=AC,
∴AB:AE=4:1.
故答案为:4:1.
三、解答题
5.【解析】如图,∵在△ABC中,∠BAC=90°,∠C=30°,AD是高,
∴∠ADB=90°,∠BAD=∠C=30°,
∴在直角△ABC中,AB=BC=2,
∴在直角△ABC中,BD=AB=1.
∴BD的长为1.
6.【解析】(1)∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴CD=DE=5,
∵∠B=30°,
∴BD=2DE=10,
(2)AE与BE相等,理由如下:
∵在△ABC中,∠C=90°,∠B=30°,
∴∠CAB=60°,
∵AD平分∠CAB交CB于点D,
∴∠DAB=30°,
∴AD=BD,
∵DE⊥AB,
∴AE=BE.
7.【证明】在△ABC中,
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
又∵AD⊥AC,
∴∠DAC=90°,
∵∠C=30°
∴CD=2AD,∠BAD=∠B=30°,
∴AD=DB,
∴BC=CD+BD=AD+DC=AD+2AD=3AD.
8.【解析】过B作BD⊥AC于D,则∠BDA=90°,
( http: / / www.21cnjy.com )
∵∠A=30°,
∴BD=AB=×8cm=4cm,
∴△ABC的面积是×AC×BD=×8cm×4cm=16cm2,
答:△ABC的面积是16cm2.
9.【解析】(1)解:∵∠BAD=15°,∠ADC=4∠BAD,
∴∠ADC=60°,
∴∠B=60°﹣15°=45°;
(2)证明:过C作CE⊥AD于E,连接EB.
( http: / / www.21cnjy.com )
∵∠ECD=90°﹣60°=30°
∴DC=2ED,
∵DC=2BD,
∴ED=BD,
∴∠DBE=∠DEB=∠ECD=30°,
∴∠EBA=45°﹣30°=15°=∠BAD,
∴AE=EC=EB,
∴∠CAD=∠ABD=45°.
10.【证明】∵在四边形ABCD中,对角线AC平分∠DAB,∠DAB=120°,∠B=∠D=90°,
∴在直角△ABC中,∠BAC=60°=∠DAC,AC公共,
∴△ABC≌△ADC(AAS),
∴∠ACB=30°=∠ACD,
∴AB=AC,
而AB=AD,
∴AB+AD=AC.
11.【解析】由题意知∠CAD=30°,∠CBD=60°,
在△BCD中,∠CBD=60°,
∴∠BCD=30°,
∴BC=2BD,
∵船从B到D走了2小时,船速为每小时40海里,
∴BD=80海里,
∴BC=160海里,
由∠CBD=60°,得∠ABC=120°,
∵∠CAD=30°,
∴∠ACB=30°,
∴AB=BC,
∴AB=160海里,
∵AD=AB+BD,
∴AD=160+80=240(海里).
因此船从A到D一共走了240海里.
12.【证明】∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵DE⊥AB,DF⊥AC,垂足为E,F,
∴DE=BD,DF=DC,
∴DE+DF=BD+DC=(BD+DC)=BC.
∴DE+DF=BC.
二、知识回顾 一、等边三角形的性质1.等边三角形的三条边相等;2.等边三角形的三个内角都相等,且都等于60°;3.等边三角形是轴对称图形,有三条对称轴;4.等边三角形每条边上的中线、高线和所对角的平分线都相互重合.二、等边三角形的判定1.三边相等的三角形是等边三角形;2.三个角都相等的三角形是等边三角形;3.有一个内角等于60°的等腰三角形是等边三角形.
三、新知讲解 含30°角的直角三角形的性质性质:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.几何语言:∵在Rt△ABC中,∠C=90°,∠A=30°,∴BC=AB. ( http: / / www.21cnjy.com )
四、典例探究 扫一扫,有惊喜哦!1.利用含30°角的直角三角形的性质求解【例1】(2014秋 乳山市期中)如图,在Rt△ABC中,∠C=90°,∠A=30°,AB+BC=12cm,则AB等于( ) ( http: / / www.21cnjy.com )A.6cm B.7cm C.8cm D.9cm总结:应用含30°角的直角三角形的性质时要注意:(1)该性质是含30°角的直角三角形特有的定理,非直角三角形或一般直角三角形不能应用;(2)应用时,要注意找准30°的角所对的直角边及斜边.【例2】(2013秋 宝塔区校级期中)如图,在△ABC中,AB=AC=2a,∠ABC =15°.求S△ABC. ( http: / / www.21cnjy.com )总结:当题目中出现15°或150°的角时 ( http: / / www.21cnjy.com ),可在三角形外作高线构造直角三角形,利用外角性质得到30°角,进而利用直角三角形中30°角所对直角边等于斜边的一半进行求解.练1.(2014秋 利通区校级期末)如图, ( http: / / www.21cnjy.com )在△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于点D,若AD=2,则:∠ACD= °,AC= ,AB= . ( http: / / www.21cnjy.com )练2.某市在“旧城改造”中,计划在市内一块如图所示的三角形空地中种植草皮美化环境,已知这种草皮每平方米要80元,求买这种草皮至少需多少元. ( http: / / www.21cnjy.com )2.利用含30°角的直角三角形证明【例3】(2012秋 福泉市期末)如图,△ABC中,∠ACB=90°,CD是高,∠A=30°,求证:BD=AB. ( http: / / www.21cnjy.com )总结:含30°角的直角三角形的性质定理为证 ( http: / / www.21cnjy.com )明一条线段是另一条线段的一半(或2倍)提供了重要的理论依据,实际证明中,往往要用到线段间的等量代换才能得证.【例4】如图,在△ABC中,AB=AC,∠BAC=120°,DE⊥AB,且BE=AE.求证:DC=2BD. ( http: / / www.21cnjy.com )总结:“30°角”的性质常常用来证明线段的倍分关系,在含30°角的直角三角形中证明有关结论,有以下四种常见思路:(1)若题目中出现含30°或60°角的直角三角形,则可直接运用性质证明;(2)若题目中只出现30°或60°的角,则可通过作高等方法构造直角三角形;(3)若题目中出现15°或150°的角,则在三角形外作高线构造直角三角形;(4)若题目中出现90°和60°(或30°)的角,但没有出现三角形,则可通过延长边等方法构造直角三角形.练3.如图,在△ABC中, ( http: / / www.21cnjy.com )∠C=90°,AD是∠BAC的平分线,过点D作DE⊥AB.DE恰好是∠ADB的平分线.CD与DB有怎样的数量关系?请说明理由. ( http: / / www.21cnjy.com )练4.(2011秋 庐阳区期末)如图: ( http: / / www.21cnjy.com )△ABC中,∠B=60°,AB=10,BC=6,D为BC上一点,且BD=2DC,连接AD.求证:AD=AC. ( http: / / www.21cnjy.com )
五、课后小测 一、选择题1.(2013秋 建阳市期末)如图 ( http: / / www.21cnjy.com ),在Rt△ABC中,∠C=90°,∠B=30°,CD是斜边AB上的高,AD=3cm,则AB的长度是( ) ( http: / / www.21cnjy.com )A.3cm B.6cm C.9cm D.12cm2.(2015 宜城市模拟)如图, ( http: / / www.21cnjy.com )已知∠AOB=60°,点P在边OA上,OP=8,点M,N在边OB上,PM=PN,若MN=2,则ON=( ) ( http: / / www.21cnjy.com )A.6 B.5 C.4 D.3二、填空题3.(2013秋 新浦区校级月考)如图,铁路 ( http: / / www.21cnjy.com )AC与铁路AD相交于车站A,B区在∠CAD的平分线上,且距车站A为20千米,∠DAC=60°,则B区距铁路AC的距离为 千米. ( http: / / www.21cnjy.com )4.(2013秋 中江县期末)如图,在△ABC中,AB=AC,∠BAC=120°,D是BC的中点,DE⊥AC.则AB:AE= . ( http: / / www.21cnjy.com )三、解答题5.(2015春 娄底期中)如图,△ABC中,∠BAC=90°,AD是△ABC的高,∠C=30°,BC=4,求BD的长. ( http: / / www.21cnjy.com )6.(2014秋 龙口市期 ( http: / / www.21cnjy.com )末)如图,在△ABC中,∠C=90°,AD平分∠CAB交CB于点D,过点D作DE⊥AB于点E,若∠B=30°,CD=5.(1)求BD的长;(2)AE与BE相等吗?说明理由. ( http: / / www.21cnjy.com )7.(2014秋 五常市校级期中)如图,△ABC中,AB=AC,∠BAC=120°,AD⊥AC交BC于点D,求证:BC=3AD. ( http: / / www.21cnjy.com )8.(2013春 修水县校级期末)如图,在△ABC中,AB=AC=8cm,∠A=30°,求△ABC的面积. ( http: / / www.21cnjy.com )9.(2011 永嘉县校级自主招生)如图,在△ABC中,AD交边BC于点D,∠BAD=15°,∠ADC=4∠BAD,DC=2BD.(1)求∠B的度数;(2)求证:∠CAD=∠B. ( http: / / www.21cnjy.com )10.(2009 河北模拟)在四边形ABCD中,对角线AC平分∠DAB,∠DAB=120°,∠B=∠D=90°,求证:AB+AD=AC. ( http: / / www.21cnjy.com )11.(2008秋 莒南 ( http: / / www.21cnjy.com )县月考)如图,已知某船于上午8点在A处观测小岛C在北偏东60°方向上.该船以每小时40海里的速度向东航行到B处,此时测得小岛C在北偏东30°方向上.船以原速度再继续向东航行2小时到达小岛C的正南方D点.求船从A到D一共走了多少海里? ( http: / / www.21cnjy.com )12.如图,在△ABC中,AB=AC,D是BC边上的中点,DE⊥AB,DF⊥AC,垂足为E,F,∠BAC=120°,求证:DE+DF=BC. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】根据含30°角的直角三角形的性质,易知AB=2BC,联立AB+BC=12cm,即可求得AB、BC的长.
解:Rt△ABC中,∠C=90°,∠A=30°,
∴AB=2BC.
∴AB+BC=3BC=12cm,即BC=4cm,AB=2BC=8cm.
故选C.
点评:此题考查的是直角三角形中30°角的性质:在直角三角形中,30°角所对直角边等于斜边的一半.
【例2】【解析】如图,延长BA,过点C作CD⊥AD,则根据“等腰△ABC的两个底角相等”及三角形外角性质推知∠DAC=30°.由“30度角所对的直角边等于斜边的一半”得到CD=AC=a.最后由三角形的面积公式来解题.
解:如图,延长BA,过点C作CD⊥AD,
( http: / / www.21cnjy.com )
∵AB=AC
∴∠ABC=∠ACB=15°,
∵∠DAC是△ABC的外角,
∴∠DAC=30°,
∴CD=AC=a,
∴S△ABC=AB CD=×2a×a=a2.
点评:本题考查了含30度角的直角三角形的性质,等腰三角形的性质.应用时,要注意找准30°的角所对的直角边与斜边.
练1.【解析】根据同角的余角相等可得出∠ACD=∠B,可得到AC长,在直角三角形BCA中,可得出AB.
解:∵∠ACB=90°,
∴∠ACD+∠BCD=90°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠ACD+∠A=90°,
∴∠ACD=∠B=30°,
∵AD=2,
∴AC=4,
在△ABC中,∠ACB=90°,∠B=30°,
∴AB=2AC=8,
故答案为:30;4;8.
点评:本题考查了含30°角的直角三角形的性质,30°所对的直角边等于斜边的一半.是基础知识要熟练掌握.
练2.【解析】作BA边的高CD,设与B ( http: / / www.21cnjy.com )A的延长线交于点D,则∠DAC=30°,由AC=60m,即可求出CD=30m,然后根据三角形的面积公式即可推出△ABC的面积为600m2,最后根据每平方米的售价即可推出结果.
解:如图,作BA边的高CD,设与BA的延长线交于点D,
( http: / / www.21cnjy.com )
∵∠BAC=150°,
∴∠DAC=30°,
∵CD⊥BD,AC=60m,
∴CD=30m,
∵AB=40m,
∴S△ABC=AB×CD=×40×30=600m2,
∵每平方米售价80元,
∴购买这种草皮的价格为600×80=48000元.
答:买这种草皮至少需48000元.
点评:本题主要考查三角形的面积公式,含 ( http: / / www.21cnjy.com )30度角的直角三角形的性质,关键在于做出AB边上的高,根据相关的性质推出高CD的长度,正确的计算出△ABC的面积.
【例3】【解析】根据直角三角形30°角所对的直角边等于斜边的一半的性质求出BC=AB,再求出∠BCD=30°,再次利用此性质解答即可得证.
证明:∵∠ACB=90°,∠A=30°,
∴BC=AB,(直角三角形中,30°所对直角边等于斜边的一半),
∵CD是高,
∴∠ADC=90°,
∴∠ACD=60°,
∴∠BCD=30°,
∴BD=BC,
∴BD=AB.
点评:本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质,两次利用性质是解题的关键.
【例4】【解析】连接AD.在△ABC中,根据等边对等角的性质及三角形内角和定理求出∠B=∠C=(180°﹣∠BAC)=30°.由DE是AB的垂直平分线得出AD=BD,那么∠BAD=∠B=30°,那么∠DAC=∠BAC﹣∠BAD=90°.然后在Rt△ADC中,根据30°角所对的直角边等于斜边的一半,得出DC=2AD,等量代换即可得到DC=2BD.
证明:连接AD.
( http: / / www.21cnjy.com )
∵在△ABC中,AB=AC,∠BAC=120°,
∴∠B=∠C=(180°﹣∠BAC)=30°.
∵DE⊥AB,BE=AE,
∴AD=BD.
∴∠BAD=∠B=30°.
∴∠DAC=∠BAC﹣∠BAD=120°﹣30°=90°.
∵在Rt△ADC中,∠DAC=90°,∠C=30°,
∴DC=2AD,
∴DC=2BD.
点评:本题考查了含30度角的直角三 ( http: / / www.21cnjy.com )角形的性质,等腰三角形的性质,三角形内角和定理,垂直平分线的性质,难度适中,熟记并灵活应用各性质是解题的关键.
练3.【解析】由条件先证△AED≌△BED,得出∠BAD=∠CAD=∠B,再根据直角三角形两锐角的和为90°,求得∠B=30°,即可得到CD=DB.
解:CD=DB.理由如下:
∵DE⊥AB,
∴∠AED=∠BED=90°,
∵DE是∠ADB的平分线,
∴∠ADE=∠BDE,
又∵DE=DE,
∴△AED≌△BED(ASA),
∴AD=BD,∠DAE=∠B,
∵∠BAD=∠CAD=∠BAC,
∴∠BAD=∠CAD=∠B,
∵AD=BD,∠BAD+∠CAD+∠B=90°,
∴∠B=∠BAD=∠CAD=30°,
在直角三角形ACD中,∠CAD=30°,
∴CD=AD=BD,
即CD=DB.
点评:本题考查了含30度角的直角三角形的 ( http: / / www.21cnjy.com )性质:在直角三角形中,30°角所对的直角边等于斜边的一半.也考查了全等三角形的判定和性质,直角三角形两锐角和为90°的性质.
练4.【解析】先过A作BC的垂线,交 ( http: / / www.21cnjy.com )BC于E,在直角三角形ABE中,利用30°角所对的边等于斜边的一半,可求BE的长,再根据已知,利用线段的和差可得E是CD的中点,从而证得△ACD是等腰三角形,即AC=AD.
证明:过A作BC的垂线,交BC于E.
( http: / / www.21cnjy.com )
∵∠B=60°,
∴∠BAE=30°,
∴BE=AB=10×=5.
∵BC=6且BD=2DC,
∴BD=4,CD=2,
∴E是CD的中点,
∴E既为垂足又为中点,
∴△ACD是等腰三角形,
∴AC=AD.
点评:本题考查了含30°角的直角三角形的性质和等腰三角形的判定,也可以运用三角函数的知识进行解答.
课后小测答案:
一、选择题
1.【解析】在Rt△ABC中,
( http: / / www.21cnjy.com )
∵CD是斜边AB上的高,
∴∠ADC=90°,
∴∠ACD=∠B=30°(同角的余角相等),
∵AD=3cm,
在Rt△ACD中,AC=2AD=6cm,
在Rt△ABC中,AB=2AC=12cm.
∴AB的长度是12cm.
故选D.
2.【解析】过P作PD⊥OB于点D,
( http: / / www.21cnjy.com )
在Rt△OPD中,∵∠ODP=90°,∠POD=60°,
∴∠OPD=30°,
∴OD=OP=×8=4,
∵PM=PN,PD⊥MN,MN=2,
∴MD=ND=MN=1,
∴ON=OD+DN=4+1=5.
故选:B.
二、填空题
3.【解析】过点B作BE⊥AC于点E,
在Rt△BAE中,BA=20,∠BAE=30°,
所以BE=AB=10.
故应填10.
( http: / / www.21cnjy.com )
4.【解析】如图,连接AD,
( http: / / www.21cnjy.com )
∵AB=AC,D是BC的中点,
∴AD⊥BC,
∵∠BAC=120°,AB=AC,
∴∠C=(180°﹣120°)=30°,
∵DE⊥AC,
∴∠ADE=∠C=30°,
在Rt△ADE中,AD=2AE,
在Rt△ACD中,AC=2AD=4AE,
∵AB=AC,
∴AB:AE=4:1.
故答案为:4:1.
三、解答题
5.【解析】如图,∵在△ABC中,∠BAC=90°,∠C=30°,AD是高,
∴∠ADB=90°,∠BAD=∠C=30°,
∴在直角△ABC中,AB=BC=2,
∴在直角△ABC中,BD=AB=1.
∴BD的长为1.
6.【解析】(1)∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴CD=DE=5,
∵∠B=30°,
∴BD=2DE=10,
(2)AE与BE相等,理由如下:
∵在△ABC中,∠C=90°,∠B=30°,
∴∠CAB=60°,
∵AD平分∠CAB交CB于点D,
∴∠DAB=30°,
∴AD=BD,
∵DE⊥AB,
∴AE=BE.
7.【证明】在△ABC中,
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
又∵AD⊥AC,
∴∠DAC=90°,
∵∠C=30°
∴CD=2AD,∠BAD=∠B=30°,
∴AD=DB,
∴BC=CD+BD=AD+DC=AD+2AD=3AD.
8.【解析】过B作BD⊥AC于D,则∠BDA=90°,
( http: / / www.21cnjy.com )
∵∠A=30°,
∴BD=AB=×8cm=4cm,
∴△ABC的面积是×AC×BD=×8cm×4cm=16cm2,
答:△ABC的面积是16cm2.
9.【解析】(1)解:∵∠BAD=15°,∠ADC=4∠BAD,
∴∠ADC=60°,
∴∠B=60°﹣15°=45°;
(2)证明:过C作CE⊥AD于E,连接EB.
( http: / / www.21cnjy.com )
∵∠ECD=90°﹣60°=30°
∴DC=2ED,
∵DC=2BD,
∴ED=BD,
∴∠DBE=∠DEB=∠ECD=30°,
∴∠EBA=45°﹣30°=15°=∠BAD,
∴AE=EC=EB,
∴∠CAD=∠ABD=45°.
10.【证明】∵在四边形ABCD中,对角线AC平分∠DAB,∠DAB=120°,∠B=∠D=90°,
∴在直角△ABC中,∠BAC=60°=∠DAC,AC公共,
∴△ABC≌△ADC(AAS),
∴∠ACB=30°=∠ACD,
∴AB=AC,
而AB=AD,
∴AB+AD=AC.
11.【解析】由题意知∠CAD=30°,∠CBD=60°,
在△BCD中,∠CBD=60°,
∴∠BCD=30°,
∴BC=2BD,
∵船从B到D走了2小时,船速为每小时40海里,
∴BD=80海里,
∴BC=160海里,
由∠CBD=60°,得∠ABC=120°,
∵∠CAD=30°,
∴∠ACB=30°,
∴AB=BC,
∴AB=160海里,
∵AD=AB+BD,
∴AD=160+80=240(海里).
因此船从A到D一共走了240海里.
12.【证明】∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵DE⊥AB,DF⊥AC,垂足为E,F,
∴DE=BD,DF=DC,
∴DE+DF=BD+DC=(BD+DC)=BC.
∴DE+DF=BC.
