【多媒体导学案】人教版数学八年级上册第十三章第8课时 等腰三角形的判定与性质(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学八年级上册第十三章第8课时 等腰三角形的判定与性质(教师版) |

|
|
| 格式 | zip | ||
| 文件大小 | 170.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-10 00:00:00 | ||
图片预览


文档简介
一、学习目标 掌握等腰三角形的性质,并能利用它证明两个角相等、两条线段相等以及两条直线垂直;掌握等腰三角形的判定定理;熟练运用等腰三角形的判定定理与性质定理进行推理和计算.
二、知识回顾 1.等腰三角形的性质1.等腰三角形有两条边相等;2.等腰三角形的两个底角相等(简称“等边对等角”);3.等腰三角形的顶角平分线、底边上的中线、底边上的高花香重合(简称“三线合一”);4.等腰三角形是轴对称图形,顶角平分线所在的直线是它的对称轴.“等边对等角”揭示了三角形中边相等与角相 ( http: / / www.21cnjy.com )等的关系,由两边相等推出两角相等,是证明两角相等常用的依据之一.“三线合一”是证明两条线段相等、两个角相等以及两条直线互相垂直的重要依据.3.等腰三角形的判定1.如果一个三角形中有两条边相等,那么这个三角形是等腰三角形;2.如果一个三角形中有两个角相等,那么这两个角所对的边相等(简称“等角对等边”);3.线段垂直平分线上的点到线段两端点的距离相等.“等角对等边”揭示了三角形中角与边的转化关系,它是证明线段相等的重要定理,也是把三角形中角相等的关系转化为边相等关系的重要依据.
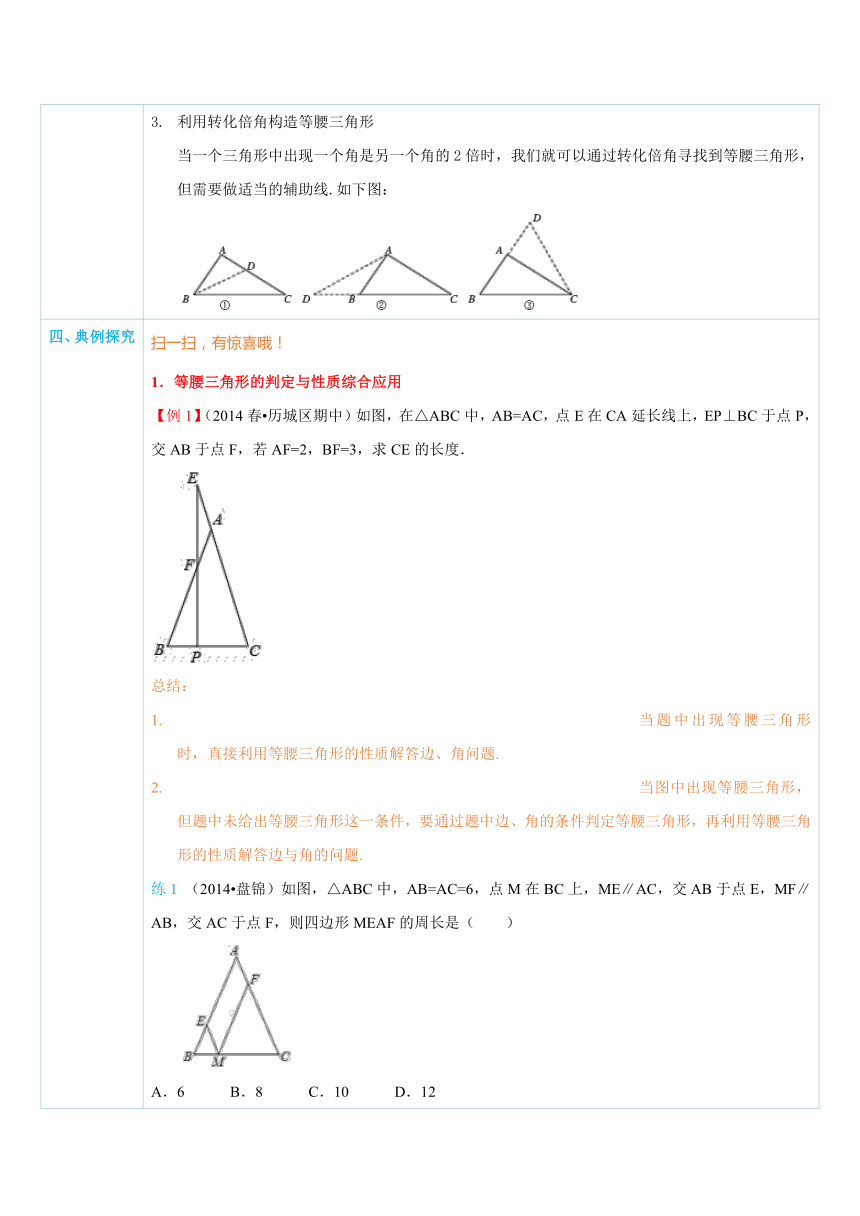
三、新知讲解 构造等腰三角形解题的常见途径利用角平分线+平分线构造等腰三角形当一个三角形中出现角平分线和平行线时,我们就可以寻找到等腰三角形.如下图: ( http: / / www.21cnjy.com )利用角平分线+垂线构造等腰三角形当一个三角形中出现角平分线和垂线时,我们就可以寻找到等腰三角形,但需要做适当的辅助线.如下图: ( http: / / www.21cnjy.com )利用转化倍角构造等腰三角形当一个三角形中出现一个角是另一个角的2倍时,我们就可以通过转化倍角寻找到等腰三角形,但需要做适当的辅助线.如下图: ( http: / / www.21cnjy.com )
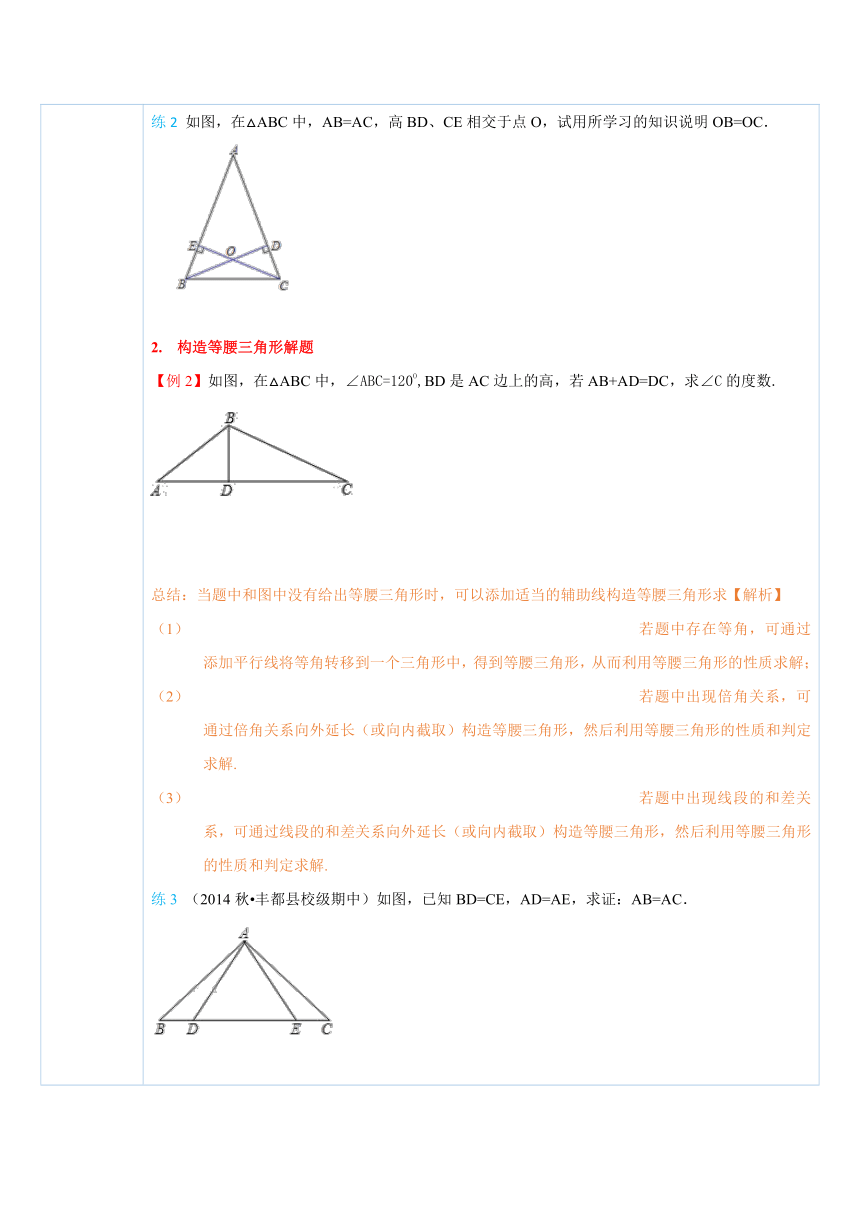
四、典例探究 扫一扫,有惊喜哦!1.等腰三角形的判定与性质综合应用 【例1】(2014春 历城区期中)如图,在 ( http: / / www.21cnjy.com )△ABC中,AB=AC,点E在CA延长线上,EP⊥BC于点P,交AB于点F,若AF=2,BF=3,求CE的长度. ( http: / / www.21cnjy.com )总结:当题中出现等腰三角形时,直接利用等腰三角形的性质解答边、角问题.当图中出现等腰三角形,但题中未给出等腰三角形这一条件,要通过题中边、角的条件判定等腰三角形,再利用等腰三角形的性质解答边与角的问题.练1 (2014 盘锦)如图,△ABC中, ( http: / / www.21cnjy.com )AB=AC=6,点M在BC上,ME∥AC,交AB于点E,MF∥AB,交AC于点F,则四边形MEAF的周长是( ) ( http: / / www.21cnjy.com )A.6 B.8 C.10 D.12练2 如图,在△ABC中,AB=AC,高BD、CE相交于点O,试用所学习的知识说明OB=OC. ( http: / / www.21cnjy.com )构造等腰三角形解题【例2】如图,在△ABC中,∠ABC=120O,BD是AC边上的高,若AB+AD=DC,求∠C的度数. ( http: / / www.21cnjy.com )总结:当题中和图中没有给出等腰三角形时,可以添加适当的辅助线构造等腰三角形求【解析】若题中存在等角,可通过添加平行线将等角转移到一个三角形中,得到等腰三角形,从而利用等腰三角形的性质求解;若题中出现倍角关系,可通过倍角关系向外延长(或向内截取)构造等腰三角形,然后利用等腰三角形的性质和判定求解.若题中出现线段的和差关系,可通过线段的和差关系向外延长(或向内截取)构造等腰三角形,然后利用等腰三角形的性质和判定求解.练3 (2014秋 丰都县校级期中)如图,已知BD=CE,AD=AE,求证:AB=AC. ( http: / / www.21cnjy.com )
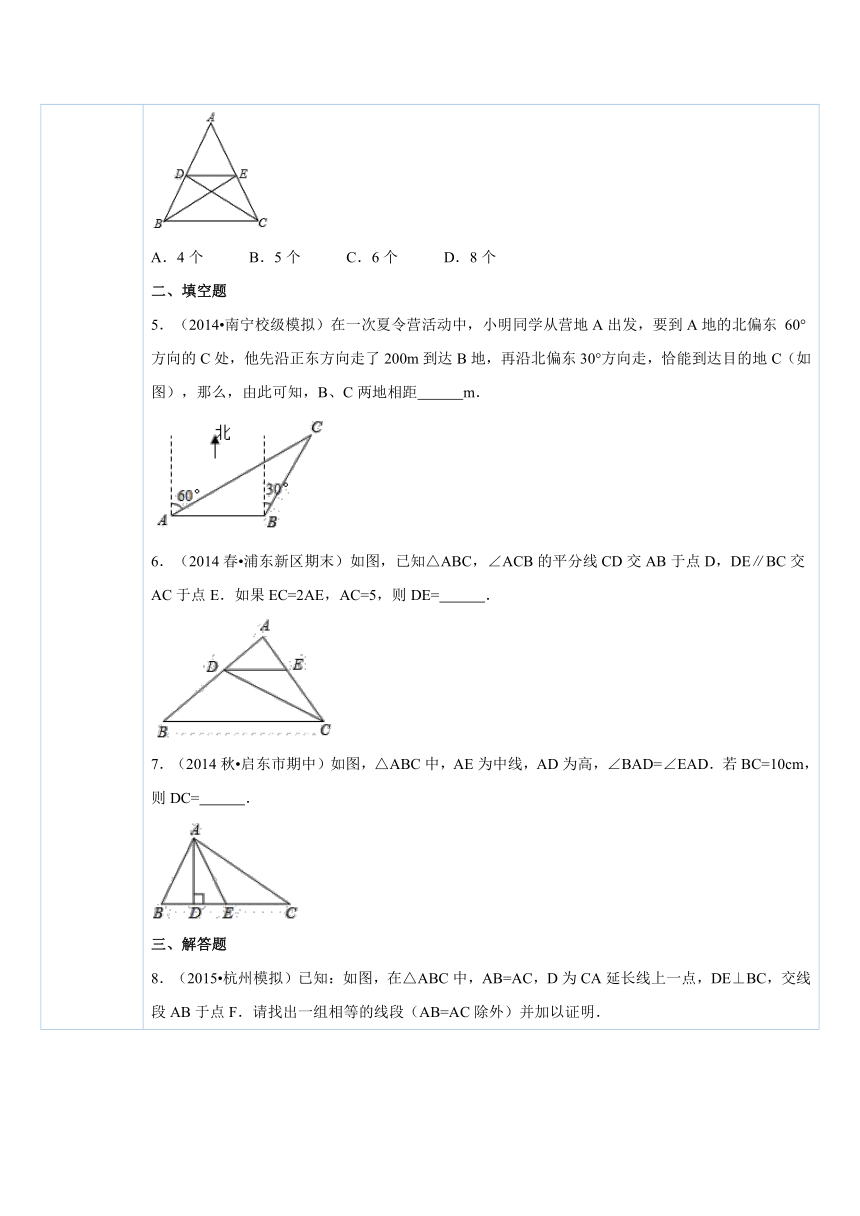
五、课后小测 一、选择题1.(2014秋 定兴县期 ( http: / / www.21cnjy.com )末)如图,△ABC中BD、CD平分∠ABC、∠ACB,过D作直线平行于BC,交AB、AC于E、F,当∠A的位置及大小变化时,线段EF和BE+CF的大小关系( ) ( http: / / www.21cnjy.com )A.EF>BE+CF B.EF=BE+CF C.EF<BE+CF D.不能确定2.(2014秋 巢湖期末)如图,∠B、∠C的平分线相交于F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论正确的是( )①△BDF、△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长为AB+AC;④BD=CE. ( http: / / www.21cnjy.com )A.③④ B.①② C.①②③ D.②③④3.(2014秋 江津区期末)如图,△ ( http: / / www.21cnjy.com )ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=8,则DF的长是( ) ( http: / / www.21cnjy.com )A.2 B.3 C. D.44.(2014秋 新泰市期末)在等腰三角形ABC中,AB=AC,BE,CD分别是底角的平分线,DE∥BC,图中等腰三角形的个数有( ) ( http: / / www.21cnjy.com )A.4个 B.5个 C.6个 D.8个二、填空题5.(2014 南宁校级模拟)在一 ( http: / / www.21cnjy.com )次夏令营活动中,小明同学从营地A出发,要到A地的北偏东 60°方向的C处,他先沿正东方向走了200m到达B地,再沿北偏东30°方向走,恰能到达目的地C(如图),那么,由此可知,B、C两地相距 m. ( http: / / www.21cnjy.com )6.(2014春 浦东新区期末)如 ( http: / / www.21cnjy.com )图,已知△ABC,∠ACB的平分线CD交AB于点D,DE∥BC交AC于点E.如果EC=2AE,AC=5,则DE= . ( http: / / www.21cnjy.com )7.(2014秋 启东市期中)如图,△ABC中,AE为中线,AD为高,∠BAD=∠EAD.若BC=10cm,则DC= . ( http: / / www.21cnjy.com )三、解答题8.(2015 杭州模拟)已知:如图,在△A ( http: / / www.21cnjy.com )BC中,AB=AC,D为CA延长线上一点,DE⊥BC,交线段AB于点F.请找出一组相等的线段(AB=AC除外)并加以证明. ( http: / / www.21cnjy.com )9.(2013秋 微山县期 ( http: / / www.21cnjy.com )末)如图,在△ABC中,BC=5cm,BP、CP分别是∠ABC和∠ACB的角平分线,且PD∥AB,PE∥AC,求△PDE的周长. ( http: / / www.21cnjy.com )10.(2013秋 海淀 ( http: / / www.21cnjy.com )区期末)在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,若AB=5,求线段DE的长. ( http: / / www.21cnjy.com )11.(2014秋 天津期末)在△ABC中,已知∠B、∠C的平分线相交于点O,过点O作EF∥BC交AB,AC于E、F.(1)图1中写出等腰三角形,并找出EF与BE、CF间的关系;(2)图2中∠ABC的平分线与三角形外 ( http: / / www.21cnjy.com )角∠ACG的平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F,这时图中还有等腰三角形吗?如果有写出来,此时EF与BE、CF间的关系如何?说明理由. ( http: / / www.21cnjy.com )12.(2013秋 渭城区校级期末)如 ( http: / / www.21cnjy.com )图,已知:△ABC中,∠B、∠C的角平分线相交于点D,过D作EF∥BC交AB于点E,交AC于点F,AB=8cm,AC=6cm.(1)求证:BE+CF=EF.(2)求△ADE的周长. ( http: / / www.21cnjy.com )13.(2014秋 天河区期中)如图,BA⊥AD,∠ADB=∠ABD=∠DAO,∠DBC=60°,∠DCO=∠BCO.(1)求证:BD⊥AC;(2)求∠DCO的度数;(3)求证:BC=DC. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】根据等边对等角得出 ( http: / / www.21cnjy.com )∠B=∠C,再根据EP⊥BC,得出∠C+∠E=90°,∠B+∠BFP=90°,从而得出∠E=∠BFP,再根据对顶角相等得出∠BFP=∠AFE,所以∠E=∠AFE,最后根据等角对等边即可得出答案.
证明:在△ABC中,
∵AB=AC,
∴∠B=∠C.
∵EP⊥BC,
∴∠C+∠E=90°,∠B+∠BFP=90°,
∴∠E=∠BFP,
又∵∠BFP=∠AFE,
∴∠E=∠AFE,
∴AF=AE,
∴△AEF是等腰三角形.
又∵AF=2,BF=3,
∴CA=AB=5,AE=2,
∴CE=7.
点评:本题考查了等腰三角形的判定和性质,解题的关键是证明∠E=∠AFE,注意等边对等角,以及等角对等边的灵活使用.
练1.【解析】∵ME∥AC,MF∥AB,
则四边形AEMF是平行四边形,
∠B=∠FMC,∠EMB=∠C
∵AB=AC,∴∠B=∠C,
∴∠B=∠EMB,∠C=∠FMC
∴BE=EM,FM=FC,
所以: AFDE的周长等于AE+EM+AF+FM=(AE+BE)+(AF+FC)=AB+AC=12.
故选:D.
练2.【解析】先根据AB=AC,可得∠A ( http: / / www.21cnjy.com )BC=∠ACB,再由垂直可得90°的角,在△BCE和△BCD中,利用内角和为180°,可分别求∠BCE和∠DBC,利用等量减等量差相等,可证.
解:∵AB=AC,
∴∠ABC=∠ACB.
∵BD、CE分别是高,
∴BD⊥AC,CE⊥AB.
∴∠CEB=∠BDC=90°.
∴∠ECB=90°-∠ABC,∠DBC=90°-∠ACB.
∠ECB=∠DBC.
∴OB=OC.
点评:本题考查了等腰三角形的性质及三角形的内角和定理;等量减等量差相等的利用是解答本题的关键.
【例2】【解析】延长DA到E,使AE ( http: / / www.21cnjy.com )=AB,从而求出DE=DC,然后根据线段垂直平分线上的点到线段两端点的距离相等可得BC=BE,再根据等边对等角可得∠C=∠E,∠E=∠ABE,再根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠BAD,然后根据三角形的内角和定理列式计算即可得解.
解:如图,延长DA到E,使AE=AB,
∵AB+AD=DC,
∴AE+AD=AB+AD=DC,
又∵BD是AC边上的高,
∴BD是CE的垂直平分线,
∴BC=BE.
根据等边对等角,得∠C=∠E,∠E=∠ABE,
根据三角形的外角性质,得∠BAD=∠E+∠ABE=2∠C,
又∵在△ABC中,∠BAD+∠C+∠ABC=180O,
∴2∠C+∠C+120O=180O,
解得∠C=20O.
点评:本题考查了等腰三角形的判定与性质 ( http: / / www.21cnjy.com ),线段垂直平分线上的点到线段两端点的距离相等的性质,利用“补长”法作辅助线构造出等腰三角形是解题的关键.
练3.【解析】过点F作AF⊥BC于点F,
( http: / / www.21cnjy.com )
∵AD=AE,
∴DF=EF,
∵BD=CE,
∴BF=CF,
∴AB=AC.
课后小测答案:
一、选择题
1.【解析】由BD平分∠ABC得,∠EBD=∠ABC,
∵EF∥BC,
∴∠AEF=∠ABC=2∠EBD,∠AEF=∠EBD+∠EDB,
∴∠EBD=∠EDB,
∴△BED是等腰三角形,
∴ED=BE,
同理可得,DF=FC,(△CFD是等腰三角形)
∴EF=ED+EF=BE+FC,
∴EF=BE+CF.
故选B.
2.【解析】∵DE∥BC,
∴∠DFB=∠FBC,∠EFC=∠FCB,
∵BF是∠ABC的平分线,CF是∠ACB的平分线,
∴∠FBC=∠DFB,∠FCE=∠FCB,
∵∠DBF=∠DFB,∠EFC=∠ECF,
∴△DFB,△FEC都是等腰三角形.
∴DF=DB,FE=EC,即有DE=DF+FE=DB+EC,
∴△ADE的周长AD+AE+DE=AD+AE+DB+EC=AB+AC.
故选C.
3.【解析】∵△ABC中,D、E分别是BC、AC的中点,
∴DE∥AB,BD=BC=4,
∴∠ABF=∠BFD,
∵BF平分∠ABC,
∴∠FBC=∠ABF,
∴∠BFD=∠DBF,
∴DB=DF=4,
故选D.
4.【解析】如图,
( http: / / www.21cnjy.com )
∵AB=AC,
∴∠ABC=∠ACB(设为2α);
∵DE∥BC,
∴∠ADE=∠AED=2α;∠DEO=∠CBO=α,∠EDO=∠BCO=α;
∵BE,CD分别是底角的平分线,
∴∠ABE=∠CBE=α,∠ACD=∠BCD=α,
∴∠DBE=∠DEB,∠EDC=∠ECD,∠ODE=∠OED,∠OBC=∠OCB,
∴AD=AE、OD=OE、OB=OC、BD=ED、CE=DE,
∴图中共有6个等腰三角形,
故选C.
二、填空题
5.【解析】∵B在A的正东方,C在A地的北偏东 60°方向,
∴∠BAC=90°﹣60°=30°,
∵C在B地的北偏东30°方向,
∴∠ABC=90°+30°=120°,
∴∠C=180°﹣∠BAC﹣∠ABC=180°﹣30°﹣120°=30°,
∴∠BAC=∠C,
∴BC=AB=200m.
故答案为:200.
6.【解析】∵DC平分∠ACB,
∴∠BCD=∠ACD,
∵DE∥BC,
∴∠EDC=∠BCD,
∴∠EDC=∠ACD,
∴ED=EC,
∵EC=2AE,AC=5,
∴EC=AC=
∴DE=.
故答案为:.
7.【解析】∵AD为高,∠BAD=∠EAD,
∴BD=DE,
∵AE为中线,BC=10cm,
∴BE=CE=BC=5cm,
∴DE=BE=2.5(cm),
∴DC=DE+EC=7.5(cm).
故答案为:7.5cm.
三、解答题
8.【解析】AD=AF;
证明:∵AB=AC,
∴∠B=∠C
∵DE⊥BC,
∴∠BEF=∠DEC=90°,
∴∠BFE=∠D,
∵∠BFE=∠DFA,
∴∠DFA=∠D,
∴AF=AD.
( http: / / www.21cnjy.com )
9.【解析】∵BP、CP分别是∠ABC和∠ACB的角平分线,
∴∠ABP=∠PBD,∠ACP=∠PCE,
∵PD∥AB,PE∥AC,
∴∠ABP=∠DPB,∠ACP=∠CPE,
∴∠PBD=∠DPB,∠PCE=∠CPE,
∴BD=PD,EC=PE,
∵BC=5cm,
∴△PDE的周长为:PD+DE+PE=BD+DE+EC=BC=5(cm).
10.【解析】∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵DE∥AC,
∴∠CAD=∠ADE,
∴∠BAD=∠ADE,
∴AE=DE,
∵AD⊥DB,
∴∠ADB=90°,
∴∠EAD+∠ABD=90°,∠ADE+∠BDE=∠ADB=90°,
∴∠ABD=∠BDE,
∴DE=BE,
∵AB=5,
∴DE=BE=AE=AB=2.5.
11.【解析】(1)图中的等腰三角形有△BEO和△CFO.
∵EF∥BC,
∴∠EOB=∠OBC.
∵∠EBO=∠OBC,
∴∠EOB=∠EBO,
∴△BEO是等腰三角形;
同理可证:△CFO是等腰三角形;
(2)EF=BE﹣CF.
理由:∵BO平分∠ABC,
∴∠ABO=∠OBC.
又∵EO∥BC,
∴∠EOB=∠OBC;
∴∠ABO=∠EOB,
∴BE=EO;
同理可证:CF=FO;
∵EF=EO﹣FO,
∴EF=BE﹣CF.
12.【解析】(1)证明:∵BD平分∠ABC,
∴∠EBD=∠DBC,
∵EF∥BC,
∴∠EDB=∠DBC,
∴∠EDB=∠EBD,
∴DE=BE,
同理CF=DF,
∴EF=DE+DF=BE+CF,
即BE+CF=EF.
(2)【解析】∵BE=ED,DF=DC,
∴△AEF的周长=AE+AF+EF=AB+AC=8+6=14(厘米).
13.【解析】(1)证明:
∵BA⊥AD,
∴∠BAD=90°,
∴∠ABD=∠ADB=45°,
∴∠DAO=45°,
∴∠AOD=90°,
∴BD⊥AC;
(2)【解析】
∵∠DCO=∠BCO,且∠DBC=60°,
∴∠DCO=∠BCO=30°;
(3)证明:
由(1)可知O为BD中点,且AC⊥BD,
∴AC垂直平分BD,
∴BC=DC.
二、知识回顾 1.等腰三角形的性质1.等腰三角形有两条边相等;2.等腰三角形的两个底角相等(简称“等边对等角”);3.等腰三角形的顶角平分线、底边上的中线、底边上的高花香重合(简称“三线合一”);4.等腰三角形是轴对称图形,顶角平分线所在的直线是它的对称轴.“等边对等角”揭示了三角形中边相等与角相 ( http: / / www.21cnjy.com )等的关系,由两边相等推出两角相等,是证明两角相等常用的依据之一.“三线合一”是证明两条线段相等、两个角相等以及两条直线互相垂直的重要依据.3.等腰三角形的判定1.如果一个三角形中有两条边相等,那么这个三角形是等腰三角形;2.如果一个三角形中有两个角相等,那么这两个角所对的边相等(简称“等角对等边”);3.线段垂直平分线上的点到线段两端点的距离相等.“等角对等边”揭示了三角形中角与边的转化关系,它是证明线段相等的重要定理,也是把三角形中角相等的关系转化为边相等关系的重要依据.
三、新知讲解 构造等腰三角形解题的常见途径利用角平分线+平分线构造等腰三角形当一个三角形中出现角平分线和平行线时,我们就可以寻找到等腰三角形.如下图: ( http: / / www.21cnjy.com )利用角平分线+垂线构造等腰三角形当一个三角形中出现角平分线和垂线时,我们就可以寻找到等腰三角形,但需要做适当的辅助线.如下图: ( http: / / www.21cnjy.com )利用转化倍角构造等腰三角形当一个三角形中出现一个角是另一个角的2倍时,我们就可以通过转化倍角寻找到等腰三角形,但需要做适当的辅助线.如下图: ( http: / / www.21cnjy.com )
四、典例探究 扫一扫,有惊喜哦!1.等腰三角形的判定与性质综合应用 【例1】(2014春 历城区期中)如图,在 ( http: / / www.21cnjy.com )△ABC中,AB=AC,点E在CA延长线上,EP⊥BC于点P,交AB于点F,若AF=2,BF=3,求CE的长度. ( http: / / www.21cnjy.com )总结:当题中出现等腰三角形时,直接利用等腰三角形的性质解答边、角问题.当图中出现等腰三角形,但题中未给出等腰三角形这一条件,要通过题中边、角的条件判定等腰三角形,再利用等腰三角形的性质解答边与角的问题.练1 (2014 盘锦)如图,△ABC中, ( http: / / www.21cnjy.com )AB=AC=6,点M在BC上,ME∥AC,交AB于点E,MF∥AB,交AC于点F,则四边形MEAF的周长是( ) ( http: / / www.21cnjy.com )A.6 B.8 C.10 D.12练2 如图,在△ABC中,AB=AC,高BD、CE相交于点O,试用所学习的知识说明OB=OC. ( http: / / www.21cnjy.com )构造等腰三角形解题【例2】如图,在△ABC中,∠ABC=120O,BD是AC边上的高,若AB+AD=DC,求∠C的度数. ( http: / / www.21cnjy.com )总结:当题中和图中没有给出等腰三角形时,可以添加适当的辅助线构造等腰三角形求【解析】若题中存在等角,可通过添加平行线将等角转移到一个三角形中,得到等腰三角形,从而利用等腰三角形的性质求解;若题中出现倍角关系,可通过倍角关系向外延长(或向内截取)构造等腰三角形,然后利用等腰三角形的性质和判定求解.若题中出现线段的和差关系,可通过线段的和差关系向外延长(或向内截取)构造等腰三角形,然后利用等腰三角形的性质和判定求解.练3 (2014秋 丰都县校级期中)如图,已知BD=CE,AD=AE,求证:AB=AC. ( http: / / www.21cnjy.com )
五、课后小测 一、选择题1.(2014秋 定兴县期 ( http: / / www.21cnjy.com )末)如图,△ABC中BD、CD平分∠ABC、∠ACB,过D作直线平行于BC,交AB、AC于E、F,当∠A的位置及大小变化时,线段EF和BE+CF的大小关系( ) ( http: / / www.21cnjy.com )A.EF>BE+CF B.EF=BE+CF C.EF<BE+CF D.不能确定2.(2014秋 巢湖期末)如图,∠B、∠C的平分线相交于F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论正确的是( )①△BDF、△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长为AB+AC;④BD=CE. ( http: / / www.21cnjy.com )A.③④ B.①② C.①②③ D.②③④3.(2014秋 江津区期末)如图,△ ( http: / / www.21cnjy.com )ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=8,则DF的长是( ) ( http: / / www.21cnjy.com )A.2 B.3 C. D.44.(2014秋 新泰市期末)在等腰三角形ABC中,AB=AC,BE,CD分别是底角的平分线,DE∥BC,图中等腰三角形的个数有( ) ( http: / / www.21cnjy.com )A.4个 B.5个 C.6个 D.8个二、填空题5.(2014 南宁校级模拟)在一 ( http: / / www.21cnjy.com )次夏令营活动中,小明同学从营地A出发,要到A地的北偏东 60°方向的C处,他先沿正东方向走了200m到达B地,再沿北偏东30°方向走,恰能到达目的地C(如图),那么,由此可知,B、C两地相距 m. ( http: / / www.21cnjy.com )6.(2014春 浦东新区期末)如 ( http: / / www.21cnjy.com )图,已知△ABC,∠ACB的平分线CD交AB于点D,DE∥BC交AC于点E.如果EC=2AE,AC=5,则DE= . ( http: / / www.21cnjy.com )7.(2014秋 启东市期中)如图,△ABC中,AE为中线,AD为高,∠BAD=∠EAD.若BC=10cm,则DC= . ( http: / / www.21cnjy.com )三、解答题8.(2015 杭州模拟)已知:如图,在△A ( http: / / www.21cnjy.com )BC中,AB=AC,D为CA延长线上一点,DE⊥BC,交线段AB于点F.请找出一组相等的线段(AB=AC除外)并加以证明. ( http: / / www.21cnjy.com )9.(2013秋 微山县期 ( http: / / www.21cnjy.com )末)如图,在△ABC中,BC=5cm,BP、CP分别是∠ABC和∠ACB的角平分线,且PD∥AB,PE∥AC,求△PDE的周长. ( http: / / www.21cnjy.com )10.(2013秋 海淀 ( http: / / www.21cnjy.com )区期末)在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,若AB=5,求线段DE的长. ( http: / / www.21cnjy.com )11.(2014秋 天津期末)在△ABC中,已知∠B、∠C的平分线相交于点O,过点O作EF∥BC交AB,AC于E、F.(1)图1中写出等腰三角形,并找出EF与BE、CF间的关系;(2)图2中∠ABC的平分线与三角形外 ( http: / / www.21cnjy.com )角∠ACG的平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F,这时图中还有等腰三角形吗?如果有写出来,此时EF与BE、CF间的关系如何?说明理由. ( http: / / www.21cnjy.com )12.(2013秋 渭城区校级期末)如 ( http: / / www.21cnjy.com )图,已知:△ABC中,∠B、∠C的角平分线相交于点D,过D作EF∥BC交AB于点E,交AC于点F,AB=8cm,AC=6cm.(1)求证:BE+CF=EF.(2)求△ADE的周长. ( http: / / www.21cnjy.com )13.(2014秋 天河区期中)如图,BA⊥AD,∠ADB=∠ABD=∠DAO,∠DBC=60°,∠DCO=∠BCO.(1)求证:BD⊥AC;(2)求∠DCO的度数;(3)求证:BC=DC. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】根据等边对等角得出 ( http: / / www.21cnjy.com )∠B=∠C,再根据EP⊥BC,得出∠C+∠E=90°,∠B+∠BFP=90°,从而得出∠E=∠BFP,再根据对顶角相等得出∠BFP=∠AFE,所以∠E=∠AFE,最后根据等角对等边即可得出答案.
证明:在△ABC中,
∵AB=AC,
∴∠B=∠C.
∵EP⊥BC,
∴∠C+∠E=90°,∠B+∠BFP=90°,
∴∠E=∠BFP,
又∵∠BFP=∠AFE,
∴∠E=∠AFE,
∴AF=AE,
∴△AEF是等腰三角形.
又∵AF=2,BF=3,
∴CA=AB=5,AE=2,
∴CE=7.
点评:本题考查了等腰三角形的判定和性质,解题的关键是证明∠E=∠AFE,注意等边对等角,以及等角对等边的灵活使用.
练1.【解析】∵ME∥AC,MF∥AB,
则四边形AEMF是平行四边形,
∠B=∠FMC,∠EMB=∠C
∵AB=AC,∴∠B=∠C,
∴∠B=∠EMB,∠C=∠FMC
∴BE=EM,FM=FC,
所以: AFDE的周长等于AE+EM+AF+FM=(AE+BE)+(AF+FC)=AB+AC=12.
故选:D.
练2.【解析】先根据AB=AC,可得∠A ( http: / / www.21cnjy.com )BC=∠ACB,再由垂直可得90°的角,在△BCE和△BCD中,利用内角和为180°,可分别求∠BCE和∠DBC,利用等量减等量差相等,可证.
解:∵AB=AC,
∴∠ABC=∠ACB.
∵BD、CE分别是高,
∴BD⊥AC,CE⊥AB.
∴∠CEB=∠BDC=90°.
∴∠ECB=90°-∠ABC,∠DBC=90°-∠ACB.
∠ECB=∠DBC.
∴OB=OC.
点评:本题考查了等腰三角形的性质及三角形的内角和定理;等量减等量差相等的利用是解答本题的关键.
【例2】【解析】延长DA到E,使AE ( http: / / www.21cnjy.com )=AB,从而求出DE=DC,然后根据线段垂直平分线上的点到线段两端点的距离相等可得BC=BE,再根据等边对等角可得∠C=∠E,∠E=∠ABE,再根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠BAD,然后根据三角形的内角和定理列式计算即可得解.
解:如图,延长DA到E,使AE=AB,
∵AB+AD=DC,
∴AE+AD=AB+AD=DC,
又∵BD是AC边上的高,
∴BD是CE的垂直平分线,
∴BC=BE.
根据等边对等角,得∠C=∠E,∠E=∠ABE,
根据三角形的外角性质,得∠BAD=∠E+∠ABE=2∠C,
又∵在△ABC中,∠BAD+∠C+∠ABC=180O,
∴2∠C+∠C+120O=180O,
解得∠C=20O.
点评:本题考查了等腰三角形的判定与性质 ( http: / / www.21cnjy.com ),线段垂直平分线上的点到线段两端点的距离相等的性质,利用“补长”法作辅助线构造出等腰三角形是解题的关键.
练3.【解析】过点F作AF⊥BC于点F,
( http: / / www.21cnjy.com )
∵AD=AE,
∴DF=EF,
∵BD=CE,
∴BF=CF,
∴AB=AC.
课后小测答案:
一、选择题
1.【解析】由BD平分∠ABC得,∠EBD=∠ABC,
∵EF∥BC,
∴∠AEF=∠ABC=2∠EBD,∠AEF=∠EBD+∠EDB,
∴∠EBD=∠EDB,
∴△BED是等腰三角形,
∴ED=BE,
同理可得,DF=FC,(△CFD是等腰三角形)
∴EF=ED+EF=BE+FC,
∴EF=BE+CF.
故选B.
2.【解析】∵DE∥BC,
∴∠DFB=∠FBC,∠EFC=∠FCB,
∵BF是∠ABC的平分线,CF是∠ACB的平分线,
∴∠FBC=∠DFB,∠FCE=∠FCB,
∵∠DBF=∠DFB,∠EFC=∠ECF,
∴△DFB,△FEC都是等腰三角形.
∴DF=DB,FE=EC,即有DE=DF+FE=DB+EC,
∴△ADE的周长AD+AE+DE=AD+AE+DB+EC=AB+AC.
故选C.
3.【解析】∵△ABC中,D、E分别是BC、AC的中点,
∴DE∥AB,BD=BC=4,
∴∠ABF=∠BFD,
∵BF平分∠ABC,
∴∠FBC=∠ABF,
∴∠BFD=∠DBF,
∴DB=DF=4,
故选D.
4.【解析】如图,
( http: / / www.21cnjy.com )
∵AB=AC,
∴∠ABC=∠ACB(设为2α);
∵DE∥BC,
∴∠ADE=∠AED=2α;∠DEO=∠CBO=α,∠EDO=∠BCO=α;
∵BE,CD分别是底角的平分线,
∴∠ABE=∠CBE=α,∠ACD=∠BCD=α,
∴∠DBE=∠DEB,∠EDC=∠ECD,∠ODE=∠OED,∠OBC=∠OCB,
∴AD=AE、OD=OE、OB=OC、BD=ED、CE=DE,
∴图中共有6个等腰三角形,
故选C.
二、填空题
5.【解析】∵B在A的正东方,C在A地的北偏东 60°方向,
∴∠BAC=90°﹣60°=30°,
∵C在B地的北偏东30°方向,
∴∠ABC=90°+30°=120°,
∴∠C=180°﹣∠BAC﹣∠ABC=180°﹣30°﹣120°=30°,
∴∠BAC=∠C,
∴BC=AB=200m.
故答案为:200.
6.【解析】∵DC平分∠ACB,
∴∠BCD=∠ACD,
∵DE∥BC,
∴∠EDC=∠BCD,
∴∠EDC=∠ACD,
∴ED=EC,
∵EC=2AE,AC=5,
∴EC=AC=
∴DE=.
故答案为:.
7.【解析】∵AD为高,∠BAD=∠EAD,
∴BD=DE,
∵AE为中线,BC=10cm,
∴BE=CE=BC=5cm,
∴DE=BE=2.5(cm),
∴DC=DE+EC=7.5(cm).
故答案为:7.5cm.
三、解答题
8.【解析】AD=AF;
证明:∵AB=AC,
∴∠B=∠C
∵DE⊥BC,
∴∠BEF=∠DEC=90°,
∴∠BFE=∠D,
∵∠BFE=∠DFA,
∴∠DFA=∠D,
∴AF=AD.
( http: / / www.21cnjy.com )
9.【解析】∵BP、CP分别是∠ABC和∠ACB的角平分线,
∴∠ABP=∠PBD,∠ACP=∠PCE,
∵PD∥AB,PE∥AC,
∴∠ABP=∠DPB,∠ACP=∠CPE,
∴∠PBD=∠DPB,∠PCE=∠CPE,
∴BD=PD,EC=PE,
∵BC=5cm,
∴△PDE的周长为:PD+DE+PE=BD+DE+EC=BC=5(cm).
10.【解析】∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵DE∥AC,
∴∠CAD=∠ADE,
∴∠BAD=∠ADE,
∴AE=DE,
∵AD⊥DB,
∴∠ADB=90°,
∴∠EAD+∠ABD=90°,∠ADE+∠BDE=∠ADB=90°,
∴∠ABD=∠BDE,
∴DE=BE,
∵AB=5,
∴DE=BE=AE=AB=2.5.
11.【解析】(1)图中的等腰三角形有△BEO和△CFO.
∵EF∥BC,
∴∠EOB=∠OBC.
∵∠EBO=∠OBC,
∴∠EOB=∠EBO,
∴△BEO是等腰三角形;
同理可证:△CFO是等腰三角形;
(2)EF=BE﹣CF.
理由:∵BO平分∠ABC,
∴∠ABO=∠OBC.
又∵EO∥BC,
∴∠EOB=∠OBC;
∴∠ABO=∠EOB,
∴BE=EO;
同理可证:CF=FO;
∵EF=EO﹣FO,
∴EF=BE﹣CF.
12.【解析】(1)证明:∵BD平分∠ABC,
∴∠EBD=∠DBC,
∵EF∥BC,
∴∠EDB=∠DBC,
∴∠EDB=∠EBD,
∴DE=BE,
同理CF=DF,
∴EF=DE+DF=BE+CF,
即BE+CF=EF.
(2)【解析】∵BE=ED,DF=DC,
∴△AEF的周长=AE+AF+EF=AB+AC=8+6=14(厘米).
13.【解析】(1)证明:
∵BA⊥AD,
∴∠BAD=90°,
∴∠ABD=∠ADB=45°,
∴∠DAO=45°,
∴∠AOD=90°,
∴BD⊥AC;
(2)【解析】
∵∠DCO=∠BCO,且∠DBC=60°,
∴∠DCO=∠BCO=30°;
(3)证明:
由(1)可知O为BD中点,且AC⊥BD,
∴AC垂直平分BD,
∴BC=DC.
