【多媒体导学案】人教版数学八年级上册第十三章第4课时 画轴对称图形(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学八年级上册第十三章第4课时 画轴对称图形(教师版) |

|
|
| 格式 | zip | ||
| 文件大小 | 237.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-10 00:00:00 | ||
图片预览


文档简介
一、学习目标 通过具体实例学画轴对称图形,认识轴对称变换,探索它的基本性质和定义;能利用轴对称进行图案设计,通过利用轴对称作图和图案设计发展实践能力;通过作轴对称图形的另一半,设计图案,锻炼克服困难的意志,培养创新精神.
二、知识回顾 1.什么样的图形是轴对称图形?什么是轴对称?如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形.2.轴对称图形或成轴对称的两个图形上的对称点与对称轴有什么联系?对称轴是任何一对对称点所连线段的垂直平分线,也就是说对称点到对称轴的距离相等.3.如何画轴对称图形的对称轴?对于轴对称图形或成轴对称的两个图形,只要找到任意一对对称点,作出对称点所连线段的垂直平分线,就可以找到它们的对称轴.
三、新知讲解 1.轴对称变换由一个平面图形得到与它成轴 ( http: / / www.21cnjy.com )对称的另一个图形的过程,叫做轴对称变换.2.轴对称变换的特征(1)成轴对称的两个图形中的任何一个图形 ( http: / / www.21cnjy.com )可以看作由另一个图形经过轴对称变换后得到,一个轴对称图形也可以看作以它的部分为基础经过轴对称变换后扩展而成的;(2)经过轴对称变换得到的新图形与原图形的形状、大小完全相同;(3)经过轴对称变换得到的新图形上的每一点都和原图形上的某一点关于对称轴对称;(4)连接任意一对对称点的线段被对称轴垂直平分;(5)当对称轴的方向和位置发生变化时,得到的图形的方向和位置也会发生变化.3.对称点的画法画某点关于某直线的对称点的一般步骤如下:(1)过已知点作已知直线(对称轴)的垂线,标出垂足;(2)在这条直线的另一侧从垂足出发截取与已知点到垂足的距离相等的线段,那么截点就是这点关于该直线的对称点.4.轴对称图形的画法(1)几何图形都可以看做由点组成,只要分别作出这些点关于对称轴的对称点,再顺次连接这些对称点,就可以得到原图形的轴对称图形;(2)对于一些直线、线段或射线,或由线段组成的图形,只要作出图形中的一些特殊点(如线段端点)的对称点,再顺次连接这些对称点,就可以得到原图形的轴对称图形.
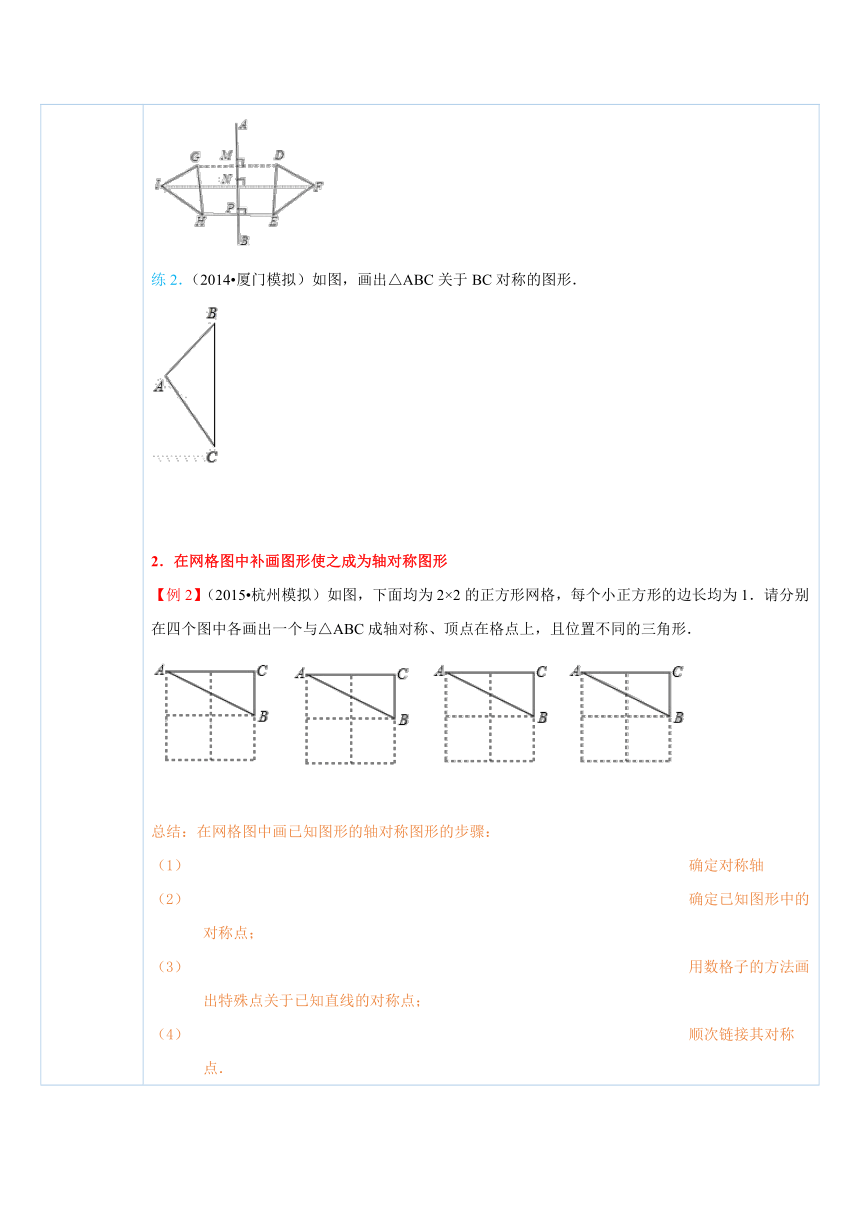
四、典例探究 扫一扫,有惊喜哦!1.画出已知图形关于某条直线对称的图形 【例1】(1)已知线段AB和直线CD,如图,画AB关于CD的轴对称图形. ( http: / / www.21cnjy.com )(2)如图,作出△ABC关于直线l的对称图形. ( http: / / www.21cnjy.com )总结:画已知图形关于直线的轴对称图形的方法:(1)找点:确定图形中的一些特殊点;(2)画点:画出特殊点关于已知直线的对称点;(3)连点:连接这些对称点,注意顺次连接.注意:所画轴对称图形用实线,其他的线可以用虚线.练1.已知直线AB和△DEF,作△DEF关于直线AB的对称图形,将作图步骤补充完整:(如图所示)(1)分别过点D,E,F作直线AB的垂线,垂足分别是点 ;(2)分别延长DM,EP,FN至 ,使 = , = , = ;(3)顺次连接 , , ,得△DEF关于直线AB的对称图形△GHI. ( http: / / www.21cnjy.com )练2.(2014 厦门模拟)如图,画出△ABC关于BC对称的图形. ( http: / / www.21cnjy.com )2.在网格图中补画图形使之成为轴对称图形【例2】(2015 杭州模拟)如图,下面均 ( http: / / www.21cnjy.com )为2×2的正方形网格,每个小正方形的边长均为1.请分别在四个图中各画出一个与△ABC成轴对称、顶点在格点上,且位置不同的三角形. ( http: / / www.21cnjy.com )总结:在网格图中画已知图形的轴对称图形的步骤:确定对称轴确定已知图形中的对称点;用数格子的方法画出特殊点关于已知直线的对称点;顺次链接其对称点.练3.如图是4×4正方形网 ( http: / / www.21cnjy.com )格,其中已有3个小方格涂成了黑色,现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有______个. ( http: / / www.21cnjy.com )
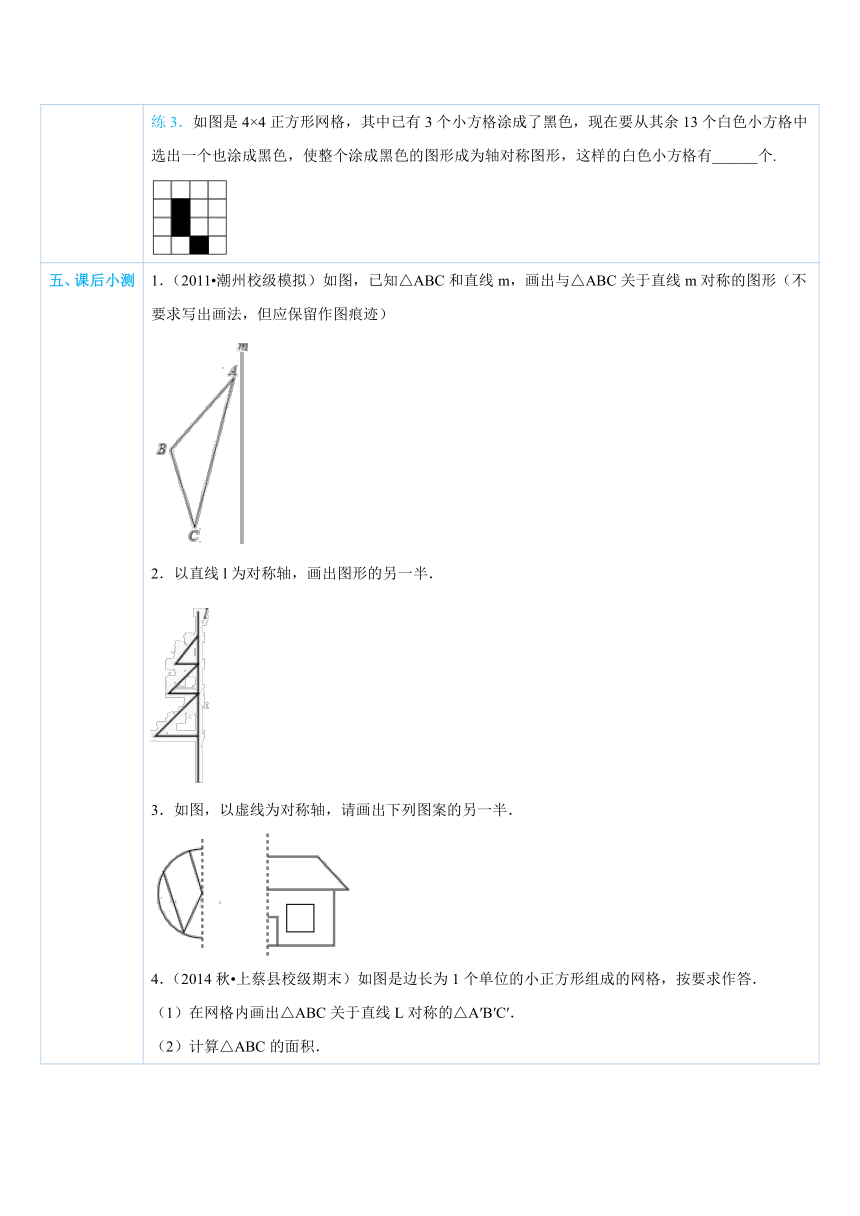
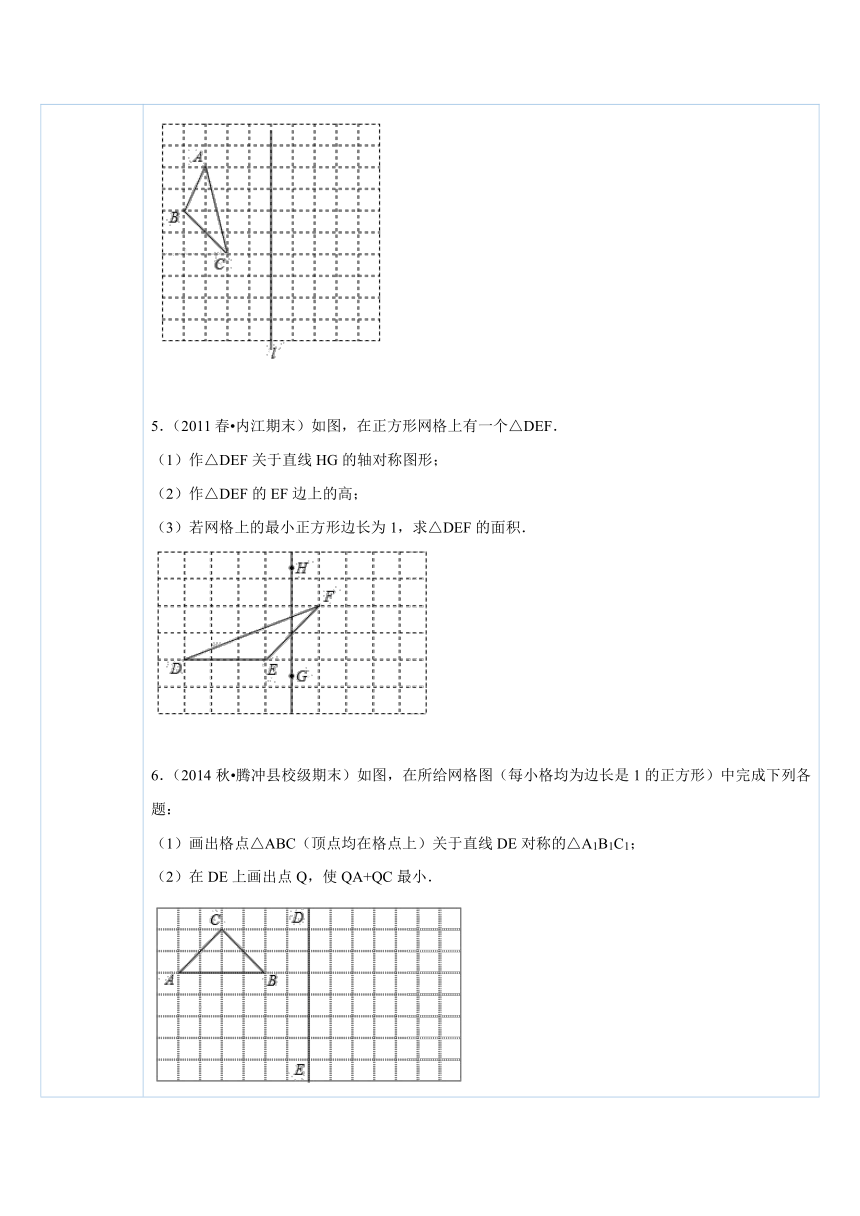
五、课后小测 1.(2011 潮州校级模拟)如图,已知△ABC和直线m,画出与△ABC关于直线m对称的图形(不要求写出画法,但应保留作图痕迹) ( http: / / www.21cnjy.com )2.以直线l为对称轴,画出图形的另一半.3.如图,以虚线为对称轴,请画出下列图案的另一半. ( http: / / www.21cnjy.com )4.(2014秋 上蔡县校级期末)如图是边长为1个单位的小正方形组成的网格,按要求作答.(1)在网格内画出△ABC关于直线L对称的△A′B′C′.(2)计算△ABC的面积. ( http: / / www.21cnjy.com )5.(2011春 内江期末)如图,在正方形网格上有一个△DEF.(1)作△DEF关于直线HG的轴对称图形;(2)作△DEF的EF边上的高;(3)若网格上的最小正方形边长为1,求△DEF的面积. ( http: / / www.21cnjy.com )6.(2014秋 腾冲县校级期末)如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;(2)在DE上画出点Q,使QA+QC最小. ( http: / / www.21cnjy.com )7.(2013秋 丹阳市校级期末)如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.(1)在图中画出与关于直线l成轴对称的△A′B′C′;(2)线段CC′被直线l ;(3)△ABC的面积为 ;(4)在直线l上找一点P,使PB+PC的长最短. ( http: / / www.21cnjy.com )8.(2014秋 厦门期末)如图,请把△ABC和△A′B′C′图形补充完整,使得它们关于直线l对称.(保留作图痕迹) ( http: / / www.21cnjy.com )9.(2013秋 泗阳县校级月考)(1)生活中因为有美丽的图案,才显得丰 ( http: / / www.21cnjy.com )富多彩,以下是来自现实生活中的三个商标(图1、2、3),请在图4,图5中画出两个是轴对称图形的新图案; ( http: / / www.21cnjy.com )(2)把图中(实线部分)补成以虚线L为对称轴的轴对称图形,你会得到一只美丽的蝴蝶案. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】根据轴对称的性质分别找到A、B的对应点A’,B’,连接A’B’即可.
解:如图所示:
( http: / / www.21cnjy.com )
点评:本题考查了轴对称作图及尺规作图的知识,注意熟练掌握作已知点关于已知直线对称点的方法.
(2)【解析】分别作出点A、B、C关于直线l的对称点A′、B′、C′,然后顺次连接即可.
解:△ABC关于直线l的对称图形△A′B′C′如图所示.
( http: / / www.21cnjy.com )
点评:本题考查了利用轴对称,熟练掌握已知点关于对称轴对称点的作法是解题的关键.
练1.【解析】作轴对称图形就是从图形的各顶点向轴引垂线并延长相同长度找对应点,顺次连接所成的图形.根据这个做法填空.
解:依据轴对称的性质得:
(1)M,P,N;
(2)点G,H,L,MG=DM,PH=EP,NL=FN;
(3)GH,HL,LG.
点评:考查的是作简单平面图形轴对称 ( http: / / www.21cnjy.com )后的图形,其依据是轴对称的性质,基本作法:①先确定图形的关键点;②利用轴对称性质作出关键点的对称点;③按原图形中的方式顺次连接对称点.
练2.【解析】作AA′⊥BC,使BC垂直平分AA′,连接A′B、A′C即可得解.
解:△ABC关于BC对称的图形如图所示.
( http: / / www.21cnjy.com )
点评:本题考查了利用轴对称变换作图,熟练掌握轴对称点的作法确定出点A的对称点是解题的关键.
【例2】【解析】根据轴对称图形的性质,不同的对称轴,可以有不同的对称图形,所以可以先找出不同的对称轴,再思考如何画对称图形.
解:
( http: / / www.21cnjy.com )
点评:作简单平面图形轴对称后的图形 ( http: / / www.21cnjy.com ),其依据是轴对称的性质.基本作法:①先确定图形的关键点;②利用轴对称性质作出关键点的对称点;③按原图形中的方式顺次连接对称点.
练3.【解析】根据轴对称图形的概念分别找出各个能成轴对称图形的小方格即可.
解:如图,有4个位置使之成为轴对称图形.
( http: / / www.21cnjy.com )
故答案为:4.
点评:此题利用方格图,考查学生对轴对称性的认识.此题关键是找对称轴,按对称轴的不同位置得到4种画法.
课后小测答案:
1.【解析】找出点A、B、C关于直线m的对称点的位置,然后顺次连接即可.
解:如图所示,△A′B′C′即为△ABC关于直线m对称的图形.
( http: / / www.21cnjy.com )
点评:本题考查了利用轴对称变换作图,准确找出点A、B、C的对称点的位置是解题的关键.
2.【解析】作AO⊥l于点O,并延长,在延长 ( http: / / www.21cnjy.com )线上截取OA′=OA,得到点A的对称点A′,同法作出左侧图形中其余关键点关于直线l的对称点,按左侧图形中的次序连接即可.
解:如图所示:
( http: / / www.21cnjy.com ).
点评:用到的知识点为:两点关于某条直线对称,那么这两点的连线被对称轴垂直平分.
3.【解析】根据轴对称图形的定义,右侧和左侧对折后重合.
解:所作图形如下所示:
( http: / / www.21cnjy.com )
点评:解答此题要明确轴对称的性质:
(1)对称轴是一条直线;
(2)垂直并且平分一条线段的直线称为这条线段的垂直平分线,或中垂线.线段垂直平分线上的点到线段两端的距离相等;
(3)在轴对称图形中,对称轴两侧的对应点到对称轴两侧的距离相等;
(4)在轴对称图形中,对称轴把图形分成完全相等的两份;
(5)如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
4.【解析】(1)利用关于轴对称图形的性质得出各对应点位置进而得出答案;
(2)利用矩形面积减去周围三角形面积求出即可.
解:(1)如图所示:△A′B′C′即为所求;
( http: / / www.21cnjy.com )
(2)△ABC的面积为:2×4﹣×1×2﹣×1×2﹣×2×2=4.
点评:此题主要考查了轴对称变换以及三角形面积,得出对应点位置是解题关键.
5.【解析】(1)根据网格结构找出点D、E、F关于直线HG的对称点D′、E′、F′的位置,然后顺次连接即可;
(2)根据网格结构以及EF的位置,过点D作小正方形的对角线,与FE的延长线相交于H,DH即为所求作的高线;
(3)DE为底边,点F到DE的距离为高,根据三角形的面积公式列式进行计算即可得解.
解:(1)如图所示,△D′E′F′即为所求作的△DEF关于直线HG的轴对称图形;
( http: / / www.21cnjy.com )
(2)如图所示,DH为EF边上的高线;
(3)△DEF的面积=×3×2=3.
点评:本题考查了利用轴对称变换作图,比较简单,熟练掌握网格结构准确找出对应点的位置是解题的关键.
6.【解析】(1)根据网格结构找出点A、B、C关于直线DE对称点A1、B1、C1的位置,然后顺次连接即可;
(2)根据轴对称确定最短路线问题连接A1C与DE的交点即为所求点Q.
解:(1)△A1B1C1如图所示;
(2)点Q如图所示.
( http: / / www.21cnjy.com )
点评:本题考查了利用轴对称变换作图,轴对称确定最短路线问题,熟练掌握网格结构准确找出对应点的位置是解题的关键.
7.【解析】(1)根据网格结构找出点B、C关于直线l的对称点B′、C′的位置,在于点A(即A′)顺次连接即可;
(2)根据轴对称的性质,对称轴垂直平分对称点的连线;
(3)利用△ABC所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解;
(4)根据轴对称确定最短路线问题,连接B′C与对称轴的交点即为所求的点P.
解:(1)△A′B′C′如图所示;
(2)线段CC′被直线l垂直平分;
(3)△ABC的面积=2×4﹣×1×2﹣×1×4﹣×2×2=8﹣1﹣2﹣2=8﹣5=3;
(4)点P如图所示.
( http: / / www.21cnjy.com )
故答案为:(2)垂直平分;(3)3.
点评:本题考查了利用轴对称变换作图,轴对称确定最短路线问题,熟练掌握网格结构准确找出对应点的位置,熟记轴对称的性质是解题的关键.
8.【解析】过点C,点B′作关于直线l的对称点,连接AB,BC,B′C及A′C′即可.
解:如图所示.
( http: / / www.21cnjy.com )
点评:本题考查的是作图﹣轴对称变换,熟知关于直线对称的点的坐标特点是解答此题的关键.
9.【解析】(1)根据线段及长方形是轴对称图形,所以可根据可在圆中画对称的线段可长方形.
(2)将三角形不在对称轴的那两个顶点分别向l轴引垂线并延长相同长度得到对应点,顺次连接.
解:(1)如图:
( http: / / www.21cnjy.com )
(2)所画图形如下:
( http: / / www.21cnjy.com ).
点评:本题主要考查了轴对称图形的性质,及垂直平分线的性质,难度不大,注意作图的标准性.
二、知识回顾 1.什么样的图形是轴对称图形?什么是轴对称?如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形.2.轴对称图形或成轴对称的两个图形上的对称点与对称轴有什么联系?对称轴是任何一对对称点所连线段的垂直平分线,也就是说对称点到对称轴的距离相等.3.如何画轴对称图形的对称轴?对于轴对称图形或成轴对称的两个图形,只要找到任意一对对称点,作出对称点所连线段的垂直平分线,就可以找到它们的对称轴.
三、新知讲解 1.轴对称变换由一个平面图形得到与它成轴 ( http: / / www.21cnjy.com )对称的另一个图形的过程,叫做轴对称变换.2.轴对称变换的特征(1)成轴对称的两个图形中的任何一个图形 ( http: / / www.21cnjy.com )可以看作由另一个图形经过轴对称变换后得到,一个轴对称图形也可以看作以它的部分为基础经过轴对称变换后扩展而成的;(2)经过轴对称变换得到的新图形与原图形的形状、大小完全相同;(3)经过轴对称变换得到的新图形上的每一点都和原图形上的某一点关于对称轴对称;(4)连接任意一对对称点的线段被对称轴垂直平分;(5)当对称轴的方向和位置发生变化时,得到的图形的方向和位置也会发生变化.3.对称点的画法画某点关于某直线的对称点的一般步骤如下:(1)过已知点作已知直线(对称轴)的垂线,标出垂足;(2)在这条直线的另一侧从垂足出发截取与已知点到垂足的距离相等的线段,那么截点就是这点关于该直线的对称点.4.轴对称图形的画法(1)几何图形都可以看做由点组成,只要分别作出这些点关于对称轴的对称点,再顺次连接这些对称点,就可以得到原图形的轴对称图形;(2)对于一些直线、线段或射线,或由线段组成的图形,只要作出图形中的一些特殊点(如线段端点)的对称点,再顺次连接这些对称点,就可以得到原图形的轴对称图形.
四、典例探究 扫一扫,有惊喜哦!1.画出已知图形关于某条直线对称的图形 【例1】(1)已知线段AB和直线CD,如图,画AB关于CD的轴对称图形. ( http: / / www.21cnjy.com )(2)如图,作出△ABC关于直线l的对称图形. ( http: / / www.21cnjy.com )总结:画已知图形关于直线的轴对称图形的方法:(1)找点:确定图形中的一些特殊点;(2)画点:画出特殊点关于已知直线的对称点;(3)连点:连接这些对称点,注意顺次连接.注意:所画轴对称图形用实线,其他的线可以用虚线.练1.已知直线AB和△DEF,作△DEF关于直线AB的对称图形,将作图步骤补充完整:(如图所示)(1)分别过点D,E,F作直线AB的垂线,垂足分别是点 ;(2)分别延长DM,EP,FN至 ,使 = , = , = ;(3)顺次连接 , , ,得△DEF关于直线AB的对称图形△GHI. ( http: / / www.21cnjy.com )练2.(2014 厦门模拟)如图,画出△ABC关于BC对称的图形. ( http: / / www.21cnjy.com )2.在网格图中补画图形使之成为轴对称图形【例2】(2015 杭州模拟)如图,下面均 ( http: / / www.21cnjy.com )为2×2的正方形网格,每个小正方形的边长均为1.请分别在四个图中各画出一个与△ABC成轴对称、顶点在格点上,且位置不同的三角形. ( http: / / www.21cnjy.com )总结:在网格图中画已知图形的轴对称图形的步骤:确定对称轴确定已知图形中的对称点;用数格子的方法画出特殊点关于已知直线的对称点;顺次链接其对称点.练3.如图是4×4正方形网 ( http: / / www.21cnjy.com )格,其中已有3个小方格涂成了黑色,现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有______个. ( http: / / www.21cnjy.com )
五、课后小测 1.(2011 潮州校级模拟)如图,已知△ABC和直线m,画出与△ABC关于直线m对称的图形(不要求写出画法,但应保留作图痕迹) ( http: / / www.21cnjy.com )2.以直线l为对称轴,画出图形的另一半.3.如图,以虚线为对称轴,请画出下列图案的另一半. ( http: / / www.21cnjy.com )4.(2014秋 上蔡县校级期末)如图是边长为1个单位的小正方形组成的网格,按要求作答.(1)在网格内画出△ABC关于直线L对称的△A′B′C′.(2)计算△ABC的面积. ( http: / / www.21cnjy.com )5.(2011春 内江期末)如图,在正方形网格上有一个△DEF.(1)作△DEF关于直线HG的轴对称图形;(2)作△DEF的EF边上的高;(3)若网格上的最小正方形边长为1,求△DEF的面积. ( http: / / www.21cnjy.com )6.(2014秋 腾冲县校级期末)如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;(2)在DE上画出点Q,使QA+QC最小. ( http: / / www.21cnjy.com )7.(2013秋 丹阳市校级期末)如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.(1)在图中画出与关于直线l成轴对称的△A′B′C′;(2)线段CC′被直线l ;(3)△ABC的面积为 ;(4)在直线l上找一点P,使PB+PC的长最短. ( http: / / www.21cnjy.com )8.(2014秋 厦门期末)如图,请把△ABC和△A′B′C′图形补充完整,使得它们关于直线l对称.(保留作图痕迹) ( http: / / www.21cnjy.com )9.(2013秋 泗阳县校级月考)(1)生活中因为有美丽的图案,才显得丰 ( http: / / www.21cnjy.com )富多彩,以下是来自现实生活中的三个商标(图1、2、3),请在图4,图5中画出两个是轴对称图形的新图案; ( http: / / www.21cnjy.com )(2)把图中(实线部分)补成以虚线L为对称轴的轴对称图形,你会得到一只美丽的蝴蝶案. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】根据轴对称的性质分别找到A、B的对应点A’,B’,连接A’B’即可.
解:如图所示:
( http: / / www.21cnjy.com )
点评:本题考查了轴对称作图及尺规作图的知识,注意熟练掌握作已知点关于已知直线对称点的方法.
(2)【解析】分别作出点A、B、C关于直线l的对称点A′、B′、C′,然后顺次连接即可.
解:△ABC关于直线l的对称图形△A′B′C′如图所示.
( http: / / www.21cnjy.com )
点评:本题考查了利用轴对称,熟练掌握已知点关于对称轴对称点的作法是解题的关键.
练1.【解析】作轴对称图形就是从图形的各顶点向轴引垂线并延长相同长度找对应点,顺次连接所成的图形.根据这个做法填空.
解:依据轴对称的性质得:
(1)M,P,N;
(2)点G,H,L,MG=DM,PH=EP,NL=FN;
(3)GH,HL,LG.
点评:考查的是作简单平面图形轴对称 ( http: / / www.21cnjy.com )后的图形,其依据是轴对称的性质,基本作法:①先确定图形的关键点;②利用轴对称性质作出关键点的对称点;③按原图形中的方式顺次连接对称点.
练2.【解析】作AA′⊥BC,使BC垂直平分AA′,连接A′B、A′C即可得解.
解:△ABC关于BC对称的图形如图所示.
( http: / / www.21cnjy.com )
点评:本题考查了利用轴对称变换作图,熟练掌握轴对称点的作法确定出点A的对称点是解题的关键.
【例2】【解析】根据轴对称图形的性质,不同的对称轴,可以有不同的对称图形,所以可以先找出不同的对称轴,再思考如何画对称图形.
解:
( http: / / www.21cnjy.com )
点评:作简单平面图形轴对称后的图形 ( http: / / www.21cnjy.com ),其依据是轴对称的性质.基本作法:①先确定图形的关键点;②利用轴对称性质作出关键点的对称点;③按原图形中的方式顺次连接对称点.
练3.【解析】根据轴对称图形的概念分别找出各个能成轴对称图形的小方格即可.
解:如图,有4个位置使之成为轴对称图形.
( http: / / www.21cnjy.com )
故答案为:4.
点评:此题利用方格图,考查学生对轴对称性的认识.此题关键是找对称轴,按对称轴的不同位置得到4种画法.
课后小测答案:
1.【解析】找出点A、B、C关于直线m的对称点的位置,然后顺次连接即可.
解:如图所示,△A′B′C′即为△ABC关于直线m对称的图形.
( http: / / www.21cnjy.com )
点评:本题考查了利用轴对称变换作图,准确找出点A、B、C的对称点的位置是解题的关键.
2.【解析】作AO⊥l于点O,并延长,在延长 ( http: / / www.21cnjy.com )线上截取OA′=OA,得到点A的对称点A′,同法作出左侧图形中其余关键点关于直线l的对称点,按左侧图形中的次序连接即可.
解:如图所示:
( http: / / www.21cnjy.com ).
点评:用到的知识点为:两点关于某条直线对称,那么这两点的连线被对称轴垂直平分.
3.【解析】根据轴对称图形的定义,右侧和左侧对折后重合.
解:所作图形如下所示:
( http: / / www.21cnjy.com )
点评:解答此题要明确轴对称的性质:
(1)对称轴是一条直线;
(2)垂直并且平分一条线段的直线称为这条线段的垂直平分线,或中垂线.线段垂直平分线上的点到线段两端的距离相等;
(3)在轴对称图形中,对称轴两侧的对应点到对称轴两侧的距离相等;
(4)在轴对称图形中,对称轴把图形分成完全相等的两份;
(5)如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
4.【解析】(1)利用关于轴对称图形的性质得出各对应点位置进而得出答案;
(2)利用矩形面积减去周围三角形面积求出即可.
解:(1)如图所示:△A′B′C′即为所求;
( http: / / www.21cnjy.com )
(2)△ABC的面积为:2×4﹣×1×2﹣×1×2﹣×2×2=4.
点评:此题主要考查了轴对称变换以及三角形面积,得出对应点位置是解题关键.
5.【解析】(1)根据网格结构找出点D、E、F关于直线HG的对称点D′、E′、F′的位置,然后顺次连接即可;
(2)根据网格结构以及EF的位置,过点D作小正方形的对角线,与FE的延长线相交于H,DH即为所求作的高线;
(3)DE为底边,点F到DE的距离为高,根据三角形的面积公式列式进行计算即可得解.
解:(1)如图所示,△D′E′F′即为所求作的△DEF关于直线HG的轴对称图形;
( http: / / www.21cnjy.com )
(2)如图所示,DH为EF边上的高线;
(3)△DEF的面积=×3×2=3.
点评:本题考查了利用轴对称变换作图,比较简单,熟练掌握网格结构准确找出对应点的位置是解题的关键.
6.【解析】(1)根据网格结构找出点A、B、C关于直线DE对称点A1、B1、C1的位置,然后顺次连接即可;
(2)根据轴对称确定最短路线问题连接A1C与DE的交点即为所求点Q.
解:(1)△A1B1C1如图所示;
(2)点Q如图所示.
( http: / / www.21cnjy.com )
点评:本题考查了利用轴对称变换作图,轴对称确定最短路线问题,熟练掌握网格结构准确找出对应点的位置是解题的关键.
7.【解析】(1)根据网格结构找出点B、C关于直线l的对称点B′、C′的位置,在于点A(即A′)顺次连接即可;
(2)根据轴对称的性质,对称轴垂直平分对称点的连线;
(3)利用△ABC所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解;
(4)根据轴对称确定最短路线问题,连接B′C与对称轴的交点即为所求的点P.
解:(1)△A′B′C′如图所示;
(2)线段CC′被直线l垂直平分;
(3)△ABC的面积=2×4﹣×1×2﹣×1×4﹣×2×2=8﹣1﹣2﹣2=8﹣5=3;
(4)点P如图所示.
( http: / / www.21cnjy.com )
故答案为:(2)垂直平分;(3)3.
点评:本题考查了利用轴对称变换作图,轴对称确定最短路线问题,熟练掌握网格结构准确找出对应点的位置,熟记轴对称的性质是解题的关键.
8.【解析】过点C,点B′作关于直线l的对称点,连接AB,BC,B′C及A′C′即可.
解:如图所示.
( http: / / www.21cnjy.com )
点评:本题考查的是作图﹣轴对称变换,熟知关于直线对称的点的坐标特点是解答此题的关键.
9.【解析】(1)根据线段及长方形是轴对称图形,所以可根据可在圆中画对称的线段可长方形.
(2)将三角形不在对称轴的那两个顶点分别向l轴引垂线并延长相同长度得到对应点,顺次连接.
解:(1)如图:
( http: / / www.21cnjy.com )
(2)所画图形如下:
( http: / / www.21cnjy.com ).
点评:本题主要考查了轴对称图形的性质,及垂直平分线的性质,难度不大,注意作图的标准性.
