【多媒体导学案】人教版数学八年级上册第十三章第2课时 线段垂直平分线的性质(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学八年级上册第十三章第2课时 线段垂直平分线的性质(教师版) |

|
|
| 格式 | zip | ||
| 文件大小 | 191.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-10 00:00:00 | ||
图片预览



文档简介
一、学习目标 理解线段垂直平分线的性质和判定;能运用线段垂直平分线的性质和判定解决实际问题;会用尺规作经过已知直线外一点作这条直线的垂线,了解作图的原理.
二、知识回顾 1.什么是线段垂直平分线?经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.2.什么是轴对称图形?线段是不是轴对称图形?如果是,说出它的对称轴在哪里?如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.线段是轴对称图形.对称轴有两条:一条是线段所在的直线;一条是线段的垂直平分线.3. 什么是尺规作图?限定用直尺和圆规来画图,成为尺规作图.4. 已经学过哪些尺规作图?(1)作线段,作一条线段等于已知线段的长;(2)作角,作一个角等于已知角;(3)作角平分线.
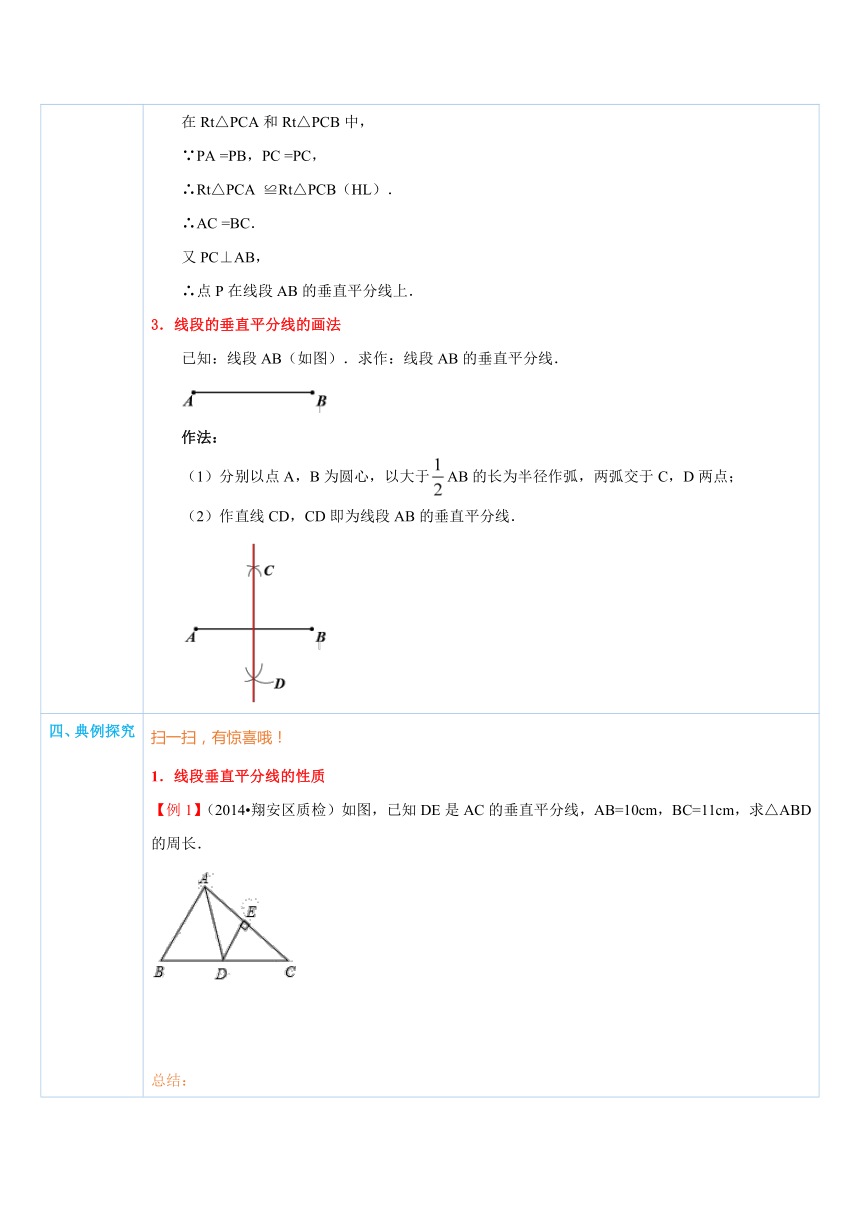
三、新知讲解 1.线段垂直平分线的性质定理文字语言:线段垂直平分线上的点与这条线段两个端点的距离相等.符号语言:∵CA=CB,l⊥AB,∴PA=PB.图示: ( http: / / www.21cnjy.com )探索与证明:已知:如图,直线l⊥AB,垂足为C,AC =CB,点P在l上.求证:PA=PB. ( http: / / www.21cnjy.com )证明:∵l⊥AB,∴∠PCA =∠PCB.又AC =CB,PC =PC,∴△PCA≌△PCB(SAS).∴PA=PB.2.线段垂直平分线的性质定理的逆定理(线段垂直平分线的判定定理)文字语言:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.符号语言:∵PA=PB,∴点P在AB的垂直平分线上.图示: ( http: / / www.21cnjy.com )探索与证明:已知:如图,PA =PB.求证:点P在线段AB的垂直平分线上.证明:过点P作线段AB 的垂线PC,垂足为C.则∠PCA=∠PCB =90°.在Rt△PCA和Rt△PCB中,∵PA =PB,PC =PC,∴Rt△PCA ≌Rt△PCB(HL).∴AC =BC.又PC⊥AB,∴点P在线段AB的垂直平分线上.3.线段的垂直平分线的画法已知:线段AB(如图).求作:线段AB的垂直平分线.作法:(1)分别以点A,B为圆心,以大于AB的长为半径作弧,两弧交于C,D两点;(2)作直线CD,CD即为线段AB的垂直平分线. ( http: / / www.21cnjy.com )
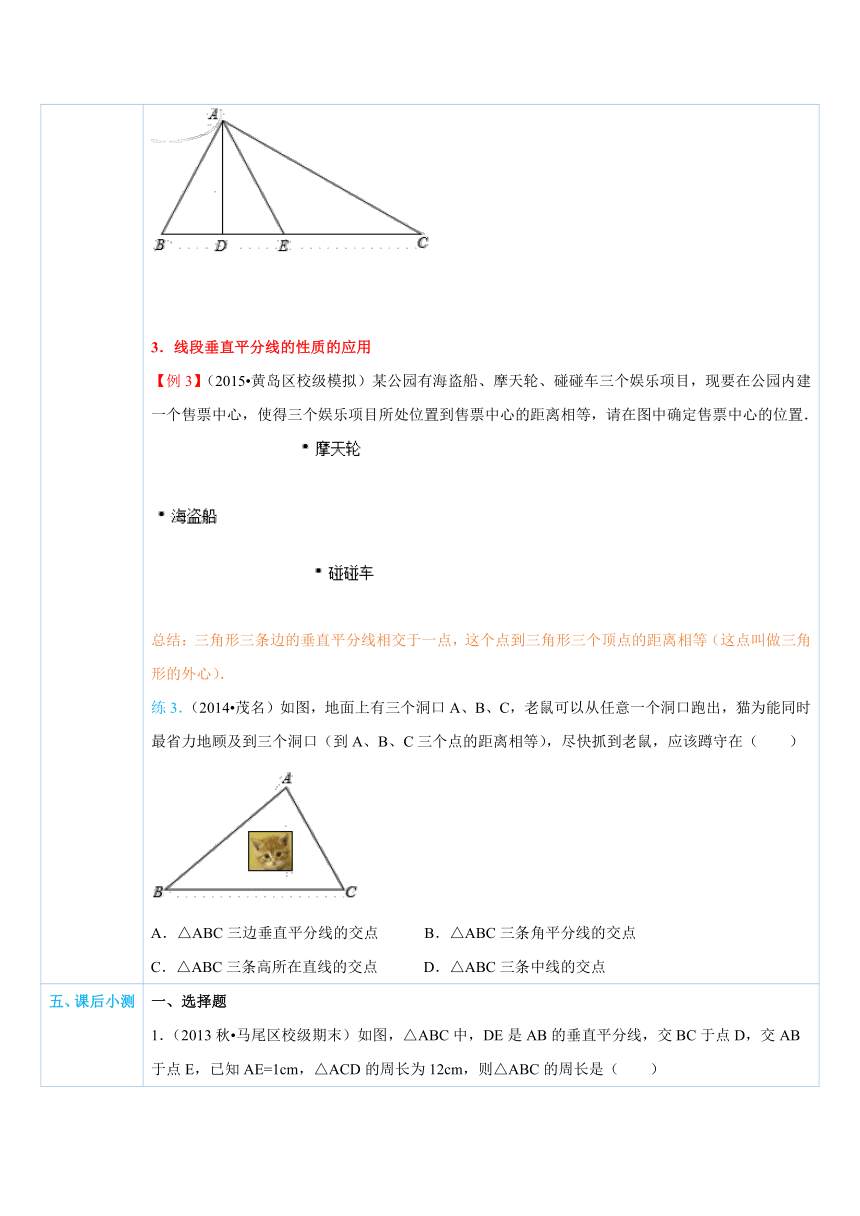
四、典例探究 扫一扫,有惊喜哦!1.线段垂直平分线的性质 【例1】(2014 翔安区质检)如图,已知DE是AC的垂直平分线,AB=10cm,BC=11cm,求△ABD的周长. ( http: / / www.21cnjy.com )总结:1.线段的垂直平分线可以看做和线段两个端点距离相等的所有点的集合.2.线段垂直平分线的性质定理是用来证明两条线段相等的根据之一.练1.(2014 甘井子区一模)如图,△ ( http: / / www.21cnjy.com )ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为( ) ( http: / / www.21cnjy.com )A.18cm B.22cm C.24cm D.26cm2.线段垂直平分线的判定【例2】(2014秋 赣州期中)如图,已知 ( http: / / www.21cnjy.com )E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C,D是垂足,连接CD,与∠AOB的平分线交于点F.求证:OE是线段CD的垂直平分线. ( http: / / www.21cnjy.com )总结:1.线段垂直平分线的判定定理常用来证明点在直线上或直线过某一点.2.判定定理中的“PA=PB”只能说明点P在线段AB的垂直平分线上,不能说明过点P的直线是线段AB的垂直平分线.3.由“两点确定一条直线”可知,要想证明直线是线段的垂直平分线,需要找出直线上的两个点,且它们到线段两端点的距离相等才行.练2.(2014春 鄄城县期中)在△ABC中,AD是高,在线段DC上取一点E,使BD=DE,已知AB+BD=DC,求证:E点在线段AC的垂直平分线上. ( http: / / www.21cnjy.com )3.线段垂直平分线的性质的应用【例3】(2015 黄岛区校级模拟)某公园 ( http: / / www.21cnjy.com )有海盗船、摩天轮、碰碰车三个娱乐项目,现要在公园内建一个售票中心,使得三个娱乐项目所处位置到售票中心的距离相等,请在图中确定售票中心的位置. ( http: / / www.21cnjy.com )总结:三角形三条边的垂直平分线相交于一点,这个点到三角形三个顶点的距离相等(这点叫做三角形的外心).练3.(2014 茂名)如 ( http: / / www.21cnjy.com )图,地面上有三个洞口A、B、C,老鼠可以从任意一个洞口跑出,猫为能同时最省力地顾及到三个洞口(到A、B、C三个点的距离相等),尽快抓到老鼠,应该蹲守在( ) ( http: / / www.21cnjy.com )A.△ABC三边垂直平分线的交点 B.△ABC三条角平分线的交点C.△ABC三条高所在直线的交点 D.△ABC三条中线的交点
五、课后小测 一、选择题1.(2013秋 马尾区校级期末)如图 ( http: / / www.21cnjy.com ),△ABC中,DE是AB的垂直平分线,交BC于点D,交AB于点E,已知AE=1cm,△ACD的周长为12cm,则△ABC的周长是( ) ( http: / / www.21cnjy.com )A.13cm B.14cm C.15cm D.16cm2.(2014春 张家口期末)如图所示,DE是线段AB的垂直平分线,下列结论一定成立的是( ) ( http: / / www.21cnjy.com )A.ED=CD B.∠DAC=∠B C.∠C>2∠B D.∠B+∠ADE=90°3.(2014秋 诸城市校级月考)如图,AB垂直平分CD,若AC=1.6cm,BC=2.3cm,则四边形ABCD的周长是( )cm. ( http: / / www.21cnjy.com )A.3.9 B.7.8 C.4 D.4.6二、填空题4.(2014秋 瓯海区期中)如图 ( http: / / www.21cnjy.com ),在△ABC中,AC=8cm,ED垂直平分AB,如果△EBC的周长是14cm,那么BC的长度为 cm. ( http: / / www.21cnjy.com )三、解答题5.(2015 黄岛区校级模拟)某 ( http: / / www.21cnjy.com )旅游景区内有一块三角形绿地ABC,如图所示,现要在道路AB的边缘上建一个休息点M,使它到A,C两个点的距离相等.在图中确定休息点M的位置. ( http: / / www.21cnjy.com )6.(2010 娄底)如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F. ( http: / / www.21cnjy.com )
求证:(1)FC=AD;
(2)AB=BC+AD.7.(2014秋 江阴市校级期中)已知直线l及其两侧两点A、B,如图.(1)在直线l上求一点P,使PA=PB;(2)在直线l上求一点Q,使l平分∠AQB.(以上两小题保留作图痕迹,标出必要的字母,不要求写作法) ( http: / / www.21cnjy.com )8.(2014秋 姜堰市校级月考)已知:如图,AD垂直平分BE,且AB+BD=DC,求证:点E在线段AC的垂直平分线上. ( http: / / www.21cnjy.com )9.(2012 贵溪市模拟)某学校正在进行校 ( http: / / www.21cnjy.com )园环境的改造工程设计,准备在校内一块四边形花坛内栽上一棵黄桷树.如图,要求黄桷树的位置点P到边AB、BC的距离相等,并且点P到点A、D的距离也相等.请用尺规作图作出栽种黄桷树的位置点P(不写作法,保留作图痕迹). ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】先根据线段垂直平分线的性质得出AD=CD,故可得出BD+AD=BD+CD=BC,进而可得出结论.
解:∵DE垂直平分AC,
∴AD=CD,
∴BD+AD=BD+CD=BC=11cm,
又∵AB=10cm,
∴△ABD的周长=AB+BD+AD=AB+BC=10+11=21(cm).
点评:本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.
练1.【解析】∵DE是AC的垂直平分线,
∴AD=CD,
∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC,
∵AE=4cm,
∴AC=2AE=2×4=8cm,
∴△ABC的周长=AB+BC+AC=14+8=22cm.
故选B.
【例2】【解析】首先根据垂 ( http: / / www.21cnjy.com )直平分线的判定定理证明点E在CD的垂直平分线上,然后根据全等证明点O也在线段CD的垂直平分线上,根据两点确定一直线和垂直平分线的唯一性即可得证.
证明:∵E是∠AOB的平分线上的一点,EC⊥OB,ED⊥OA,
∴ED=EC,(角平分线上的任意一点到角的两边的距离相等)
∴点E在线段CD的垂直平分线上,(到线段两端距离相等的点在这条线段的垂直平分线上)
∵ED⊥OA于D,EC⊥OB于C,
∴∠ODE=∠OCE=90°,
又∵OE=OE,ED=EC,
∴Rt△ODE≌Rt△OCE,(HL)
∴OD=OC,
∴点O也在线段CD的垂直平分线上,
∵点E与点O都在线段CD的垂直平分线上,
∴OE是线段CD的垂直平分线.
练2.【解析】根据线段的垂直平分线性质求出BD=DE,推出DE+EC=AE+DE,得出EC=AE,根据线段垂直平分线性质推出即可.
证明:∵AD是高,∴AD⊥BC,
又∵BD=DE,
∴AD所在的直线是线段BE的垂直平分线,
∴AB=AE,
∴AB+BD=AE+DE,
又∵AB+BD=DC,
∴DC=AE+DE,
∴DE+EC=AE+DE
∴EC=AE,
∴点E在线段AC的垂直平分线上.
点评:本题考查了线段的垂直平分线的应用,解此题的关键是熟练地运用性质进行推理,培养了学生分析问题和解决问题的能力.
【例3】【解析】由三个娱 ( http: / / www.21cnjy.com )乐项目所处位置到售票中心的距离相等,可得售票中心是海盗船、摩天轮、碰碰车三个娱乐场组成三角形的三边的垂直平分线的交点.
解:如图,①连接AB,AC,
②分别作线段AB,AC的垂直平分线,两垂直平分线相交于点P,
则P即为售票中心.
( http: / / www.21cnjy.com )
点评:此题考查了线段垂直平分线的判定.注意掌握线段垂直平分线的作法.
练3.【解析】根据题意,知猫应该到三个洞口的距离相等,则此点就是三角形三边垂直平分线的交点.
解:∵三角形三边垂直平分线的交点到三个顶点的距离相等,
∴猫应该蹲守在△ABC三边垂直平分线的交点处.
故选A.
点评:此题考查了三角形的外心的概念和性质.熟知三角形三边垂直平分线的交点到三个顶点的距离相等,是解题的关键.
课后小测答案:
一、选择题
1.【解析】∵DE是AB的垂直平分线,
∴AD=BD,AB=2AE=2
又∵△ACD的周长=AC+AD+CD=AC+BD+CD=AC+BC=12
∴△ABC的周长是12+2=14cm.
故选B
2.【解析】∵DE是线段AB的垂直平分线,
∴AD=BD.
∴∠B=∠BAD,∠ADE=∠BDE.
∴∠B+∠ADE=90°
其它选项无法证明其是正确的.
故选D
3.【解析】∵AB垂直平分CD,AC=1.6cm,BC=2.3cm,
∴AC=AD=1.6cm,BC=BD=2.3cm,
∴四边形ABCD的周长=2(AC+BC)=2×(1.6+2.3)=7.8cm.
故选B.
二、填空题
4.【解析】因为ED垂直平分AB,
所以AE=BE
则△EBC的周长是BC+CE+EB=BC+CE+EA=BC+(CE+EA)=BC+AC
又因为△EBC的周长是14cm,
所以BC+AC=14,
即BC+8=14
所以BC=6cm,BC=6cm.
三、解答题
5.【解析】作AC的垂直平分线交AB于M点,
则点M为所求.
( http: / / www.21cnjy.com )
6.【解析】(1)根据AD∥BC可知∠ ( http: / / www.21cnjy.com )ADC=∠ECF,再根据E是CD的中点可求出△ADE≌△FCE,根据全等三角形的性质即可解答.
(2)根据线段垂直平分线的性质判断出AB=BF即可.
证明:(1)∵AD∥BC(已知),
∴ ( http: / / www.21cnjy.com )∠ADC=∠ECF(两直线平行,内错角相等),
∵E是CD的中点(已知),
∴DE=EC(中点的定义).
∵在△ADE与△FCE中,
,
∴△ADE≌△FCE(ASA),
∴FC=AD(全等三角形的性质).
(2)∵△ADE≌△FCE,
∴AE=EF,AD=CF(全等三角形的对应边相等),
∴BE是线段AF的垂直平分线,
∴AB=BF=BC+CF,
∵AD=CF(已证),
∴AB=BC+AD(等量代换).
点评:此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.
7.【解析】
( http: / / www.21cnjy.com )
8.证明:∵AD垂直平分BE,
∴AD=AE,BD=DE,
∵AB+BD=DC,
∴AE+DE=DC,
∵DE+EC=DC,
∴AE=EC,
∴点E在线段AC的垂直平分线上.
9.【解析】分别作出AD的垂直平分线及∠ABC的平分线,两条直线的交点即为P点的位置.【解析】(1)①分别以A、D为圆心,以大于AD为半径画圆,两圆相交于E、F两点;
②连接EF,则EF即为线段AD的垂直平分线.
(2)①以B为圆心,以大于任意长为半径画圆,分别交AB、BC为G、H;
②分别以G、H为圆心,以大于GH为半径画圆,两圆相交于点I,连接BI,则BI即为∠ABC的平分线.
③BI与EF相交于点P,
则点P即为所求点.
( http: / / www.21cnjy.com )
点评:本题考查的是线段垂直平分线及角平分线的作法.熟知线段垂直平分线及角平分线性质是解答此题的关键.
二、知识回顾 1.什么是线段垂直平分线?经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.2.什么是轴对称图形?线段是不是轴对称图形?如果是,说出它的对称轴在哪里?如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.线段是轴对称图形.对称轴有两条:一条是线段所在的直线;一条是线段的垂直平分线.3. 什么是尺规作图?限定用直尺和圆规来画图,成为尺规作图.4. 已经学过哪些尺规作图?(1)作线段,作一条线段等于已知线段的长;(2)作角,作一个角等于已知角;(3)作角平分线.
三、新知讲解 1.线段垂直平分线的性质定理文字语言:线段垂直平分线上的点与这条线段两个端点的距离相等.符号语言:∵CA=CB,l⊥AB,∴PA=PB.图示: ( http: / / www.21cnjy.com )探索与证明:已知:如图,直线l⊥AB,垂足为C,AC =CB,点P在l上.求证:PA=PB. ( http: / / www.21cnjy.com )证明:∵l⊥AB,∴∠PCA =∠PCB.又AC =CB,PC =PC,∴△PCA≌△PCB(SAS).∴PA=PB.2.线段垂直平分线的性质定理的逆定理(线段垂直平分线的判定定理)文字语言:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.符号语言:∵PA=PB,∴点P在AB的垂直平分线上.图示: ( http: / / www.21cnjy.com )探索与证明:已知:如图,PA =PB.求证:点P在线段AB的垂直平分线上.证明:过点P作线段AB 的垂线PC,垂足为C.则∠PCA=∠PCB =90°.在Rt△PCA和Rt△PCB中,∵PA =PB,PC =PC,∴Rt△PCA ≌Rt△PCB(HL).∴AC =BC.又PC⊥AB,∴点P在线段AB的垂直平分线上.3.线段的垂直平分线的画法已知:线段AB(如图).求作:线段AB的垂直平分线.作法:(1)分别以点A,B为圆心,以大于AB的长为半径作弧,两弧交于C,D两点;(2)作直线CD,CD即为线段AB的垂直平分线. ( http: / / www.21cnjy.com )
四、典例探究 扫一扫,有惊喜哦!1.线段垂直平分线的性质 【例1】(2014 翔安区质检)如图,已知DE是AC的垂直平分线,AB=10cm,BC=11cm,求△ABD的周长. ( http: / / www.21cnjy.com )总结:1.线段的垂直平分线可以看做和线段两个端点距离相等的所有点的集合.2.线段垂直平分线的性质定理是用来证明两条线段相等的根据之一.练1.(2014 甘井子区一模)如图,△ ( http: / / www.21cnjy.com )ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为( ) ( http: / / www.21cnjy.com )A.18cm B.22cm C.24cm D.26cm2.线段垂直平分线的判定【例2】(2014秋 赣州期中)如图,已知 ( http: / / www.21cnjy.com )E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C,D是垂足,连接CD,与∠AOB的平分线交于点F.求证:OE是线段CD的垂直平分线. ( http: / / www.21cnjy.com )总结:1.线段垂直平分线的判定定理常用来证明点在直线上或直线过某一点.2.判定定理中的“PA=PB”只能说明点P在线段AB的垂直平分线上,不能说明过点P的直线是线段AB的垂直平分线.3.由“两点确定一条直线”可知,要想证明直线是线段的垂直平分线,需要找出直线上的两个点,且它们到线段两端点的距离相等才行.练2.(2014春 鄄城县期中)在△ABC中,AD是高,在线段DC上取一点E,使BD=DE,已知AB+BD=DC,求证:E点在线段AC的垂直平分线上. ( http: / / www.21cnjy.com )3.线段垂直平分线的性质的应用【例3】(2015 黄岛区校级模拟)某公园 ( http: / / www.21cnjy.com )有海盗船、摩天轮、碰碰车三个娱乐项目,现要在公园内建一个售票中心,使得三个娱乐项目所处位置到售票中心的距离相等,请在图中确定售票中心的位置. ( http: / / www.21cnjy.com )总结:三角形三条边的垂直平分线相交于一点,这个点到三角形三个顶点的距离相等(这点叫做三角形的外心).练3.(2014 茂名)如 ( http: / / www.21cnjy.com )图,地面上有三个洞口A、B、C,老鼠可以从任意一个洞口跑出,猫为能同时最省力地顾及到三个洞口(到A、B、C三个点的距离相等),尽快抓到老鼠,应该蹲守在( ) ( http: / / www.21cnjy.com )A.△ABC三边垂直平分线的交点 B.△ABC三条角平分线的交点C.△ABC三条高所在直线的交点 D.△ABC三条中线的交点
五、课后小测 一、选择题1.(2013秋 马尾区校级期末)如图 ( http: / / www.21cnjy.com ),△ABC中,DE是AB的垂直平分线,交BC于点D,交AB于点E,已知AE=1cm,△ACD的周长为12cm,则△ABC的周长是( ) ( http: / / www.21cnjy.com )A.13cm B.14cm C.15cm D.16cm2.(2014春 张家口期末)如图所示,DE是线段AB的垂直平分线,下列结论一定成立的是( ) ( http: / / www.21cnjy.com )A.ED=CD B.∠DAC=∠B C.∠C>2∠B D.∠B+∠ADE=90°3.(2014秋 诸城市校级月考)如图,AB垂直平分CD,若AC=1.6cm,BC=2.3cm,则四边形ABCD的周长是( )cm. ( http: / / www.21cnjy.com )A.3.9 B.7.8 C.4 D.4.6二、填空题4.(2014秋 瓯海区期中)如图 ( http: / / www.21cnjy.com ),在△ABC中,AC=8cm,ED垂直平分AB,如果△EBC的周长是14cm,那么BC的长度为 cm. ( http: / / www.21cnjy.com )三、解答题5.(2015 黄岛区校级模拟)某 ( http: / / www.21cnjy.com )旅游景区内有一块三角形绿地ABC,如图所示,现要在道路AB的边缘上建一个休息点M,使它到A,C两个点的距离相等.在图中确定休息点M的位置. ( http: / / www.21cnjy.com )6.(2010 娄底)如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F. ( http: / / www.21cnjy.com )
求证:(1)FC=AD;
(2)AB=BC+AD.7.(2014秋 江阴市校级期中)已知直线l及其两侧两点A、B,如图.(1)在直线l上求一点P,使PA=PB;(2)在直线l上求一点Q,使l平分∠AQB.(以上两小题保留作图痕迹,标出必要的字母,不要求写作法) ( http: / / www.21cnjy.com )8.(2014秋 姜堰市校级月考)已知:如图,AD垂直平分BE,且AB+BD=DC,求证:点E在线段AC的垂直平分线上. ( http: / / www.21cnjy.com )9.(2012 贵溪市模拟)某学校正在进行校 ( http: / / www.21cnjy.com )园环境的改造工程设计,准备在校内一块四边形花坛内栽上一棵黄桷树.如图,要求黄桷树的位置点P到边AB、BC的距离相等,并且点P到点A、D的距离也相等.请用尺规作图作出栽种黄桷树的位置点P(不写作法,保留作图痕迹). ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】先根据线段垂直平分线的性质得出AD=CD,故可得出BD+AD=BD+CD=BC,进而可得出结论.
解:∵DE垂直平分AC,
∴AD=CD,
∴BD+AD=BD+CD=BC=11cm,
又∵AB=10cm,
∴△ABD的周长=AB+BD+AD=AB+BC=10+11=21(cm).
点评:本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.
练1.【解析】∵DE是AC的垂直平分线,
∴AD=CD,
∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC,
∵AE=4cm,
∴AC=2AE=2×4=8cm,
∴△ABC的周长=AB+BC+AC=14+8=22cm.
故选B.
【例2】【解析】首先根据垂 ( http: / / www.21cnjy.com )直平分线的判定定理证明点E在CD的垂直平分线上,然后根据全等证明点O也在线段CD的垂直平分线上,根据两点确定一直线和垂直平分线的唯一性即可得证.
证明:∵E是∠AOB的平分线上的一点,EC⊥OB,ED⊥OA,
∴ED=EC,(角平分线上的任意一点到角的两边的距离相等)
∴点E在线段CD的垂直平分线上,(到线段两端距离相等的点在这条线段的垂直平分线上)
∵ED⊥OA于D,EC⊥OB于C,
∴∠ODE=∠OCE=90°,
又∵OE=OE,ED=EC,
∴Rt△ODE≌Rt△OCE,(HL)
∴OD=OC,
∴点O也在线段CD的垂直平分线上,
∵点E与点O都在线段CD的垂直平分线上,
∴OE是线段CD的垂直平分线.
练2.【解析】根据线段的垂直平分线性质求出BD=DE,推出DE+EC=AE+DE,得出EC=AE,根据线段垂直平分线性质推出即可.
证明:∵AD是高,∴AD⊥BC,
又∵BD=DE,
∴AD所在的直线是线段BE的垂直平分线,
∴AB=AE,
∴AB+BD=AE+DE,
又∵AB+BD=DC,
∴DC=AE+DE,
∴DE+EC=AE+DE
∴EC=AE,
∴点E在线段AC的垂直平分线上.
点评:本题考查了线段的垂直平分线的应用,解此题的关键是熟练地运用性质进行推理,培养了学生分析问题和解决问题的能力.
【例3】【解析】由三个娱 ( http: / / www.21cnjy.com )乐项目所处位置到售票中心的距离相等,可得售票中心是海盗船、摩天轮、碰碰车三个娱乐场组成三角形的三边的垂直平分线的交点.
解:如图,①连接AB,AC,
②分别作线段AB,AC的垂直平分线,两垂直平分线相交于点P,
则P即为售票中心.
( http: / / www.21cnjy.com )
点评:此题考查了线段垂直平分线的判定.注意掌握线段垂直平分线的作法.
练3.【解析】根据题意,知猫应该到三个洞口的距离相等,则此点就是三角形三边垂直平分线的交点.
解:∵三角形三边垂直平分线的交点到三个顶点的距离相等,
∴猫应该蹲守在△ABC三边垂直平分线的交点处.
故选A.
点评:此题考查了三角形的外心的概念和性质.熟知三角形三边垂直平分线的交点到三个顶点的距离相等,是解题的关键.
课后小测答案:
一、选择题
1.【解析】∵DE是AB的垂直平分线,
∴AD=BD,AB=2AE=2
又∵△ACD的周长=AC+AD+CD=AC+BD+CD=AC+BC=12
∴△ABC的周长是12+2=14cm.
故选B
2.【解析】∵DE是线段AB的垂直平分线,
∴AD=BD.
∴∠B=∠BAD,∠ADE=∠BDE.
∴∠B+∠ADE=90°
其它选项无法证明其是正确的.
故选D
3.【解析】∵AB垂直平分CD,AC=1.6cm,BC=2.3cm,
∴AC=AD=1.6cm,BC=BD=2.3cm,
∴四边形ABCD的周长=2(AC+BC)=2×(1.6+2.3)=7.8cm.
故选B.
二、填空题
4.【解析】因为ED垂直平分AB,
所以AE=BE
则△EBC的周长是BC+CE+EB=BC+CE+EA=BC+(CE+EA)=BC+AC
又因为△EBC的周长是14cm,
所以BC+AC=14,
即BC+8=14
所以BC=6cm,BC=6cm.
三、解答题
5.【解析】作AC的垂直平分线交AB于M点,
则点M为所求.
( http: / / www.21cnjy.com )
6.【解析】(1)根据AD∥BC可知∠ ( http: / / www.21cnjy.com )ADC=∠ECF,再根据E是CD的中点可求出△ADE≌△FCE,根据全等三角形的性质即可解答.
(2)根据线段垂直平分线的性质判断出AB=BF即可.
证明:(1)∵AD∥BC(已知),
∴ ( http: / / www.21cnjy.com )∠ADC=∠ECF(两直线平行,内错角相等),
∵E是CD的中点(已知),
∴DE=EC(中点的定义).
∵在△ADE与△FCE中,
,
∴△ADE≌△FCE(ASA),
∴FC=AD(全等三角形的性质).
(2)∵△ADE≌△FCE,
∴AE=EF,AD=CF(全等三角形的对应边相等),
∴BE是线段AF的垂直平分线,
∴AB=BF=BC+CF,
∵AD=CF(已证),
∴AB=BC+AD(等量代换).
点评:此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.
7.【解析】
( http: / / www.21cnjy.com )
8.证明:∵AD垂直平分BE,
∴AD=AE,BD=DE,
∵AB+BD=DC,
∴AE+DE=DC,
∵DE+EC=DC,
∴AE=EC,
∴点E在线段AC的垂直平分线上.
9.【解析】分别作出AD的垂直平分线及∠ABC的平分线,两条直线的交点即为P点的位置.【解析】(1)①分别以A、D为圆心,以大于AD为半径画圆,两圆相交于E、F两点;
②连接EF,则EF即为线段AD的垂直平分线.
(2)①以B为圆心,以大于任意长为半径画圆,分别交AB、BC为G、H;
②分别以G、H为圆心,以大于GH为半径画圆,两圆相交于点I,连接BI,则BI即为∠ABC的平分线.
③BI与EF相交于点P,
则点P即为所求点.
( http: / / www.21cnjy.com )
点评:本题考查的是线段垂直平分线及角平分线的作法.熟知线段垂直平分线及角平分线性质是解答此题的关键.
