湖北省鄂州市临空经济区部分学校2023-2024学年九年级下学期第一次月考数学试题(无答案)
文档属性
| 名称 | 湖北省鄂州市临空经济区部分学校2023-2024学年九年级下学期第一次月考数学试题(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 692.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-04 15:16:02 | ||
图片预览

文档简介
2024年春九年级第一次月考数学试题
一、选择题(每小题3分,共30分)
1.的倒数是( )
A. B. C. D.3
2.2022年,广东省外贸进出口总值再创新高,达到83100亿元,那么“83100”用科学记数法表示为( )
A. B. C. D.
3.下列几何体中,同一个几何体从正面看和从上面看形状图不同的是( )
A. B. C. D.
4.如图,直线,直线与分别交于两点,过点作,垂足为,若,则的度数是( )
A. B. C. D.
5.在九年级体育考试中,某校某班参加仰卧起坐测试的8名女生成绩如下:(单位:次/分):44,45,42,48,46,43,47,45,,则这组数据的众数和中位数分别为( )
A.45,44 B.45,45 C.44,46 D.45,45.5
6.袋子里有8个红球,个白球,3个黑球,每个球除颜色外都相同,从中任意摸出一个球,若摸到红球的可能性最大,则的值不可能是( )
A.1 B.3 C.5 D.10
7.某品牌手机原来每部售价为1999元,经过连续两次降价后,该手机每部售价为1360元,设平均每次降价的百分率为,根据题意,所列方程正确的是( )
A. B. C. D.
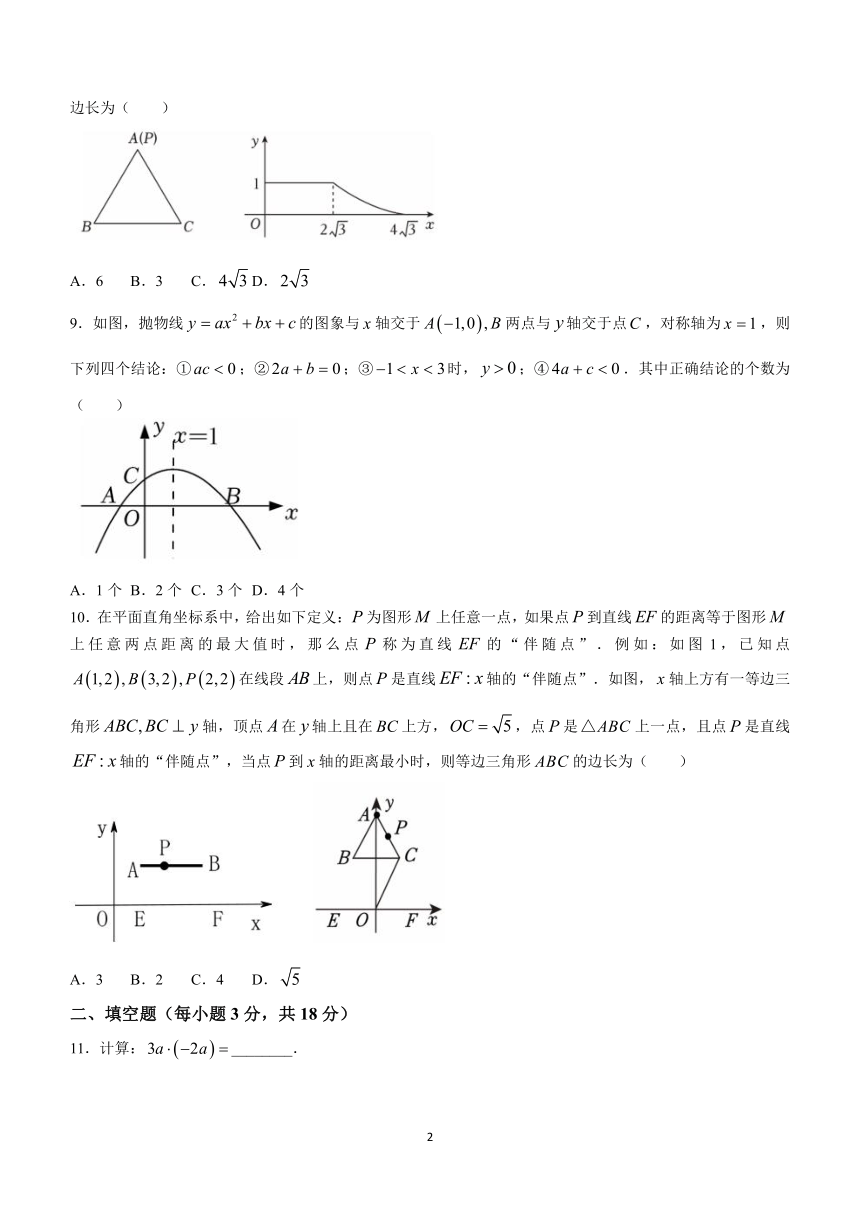
8.如图1,点从等边三角形的顶点出发,沿直线运动到三角形内部一点,再从该点沿直线运动到顶点.设点运动的路程为,图2是点运动时随变化的关系图象,则等边三角形的边长为( )
A.6 B.3 C. D.
9.如图,抛物线的图象与轴交于两点与轴交于点,对称轴为,则下列四个结论:①;②;③时,;④.其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
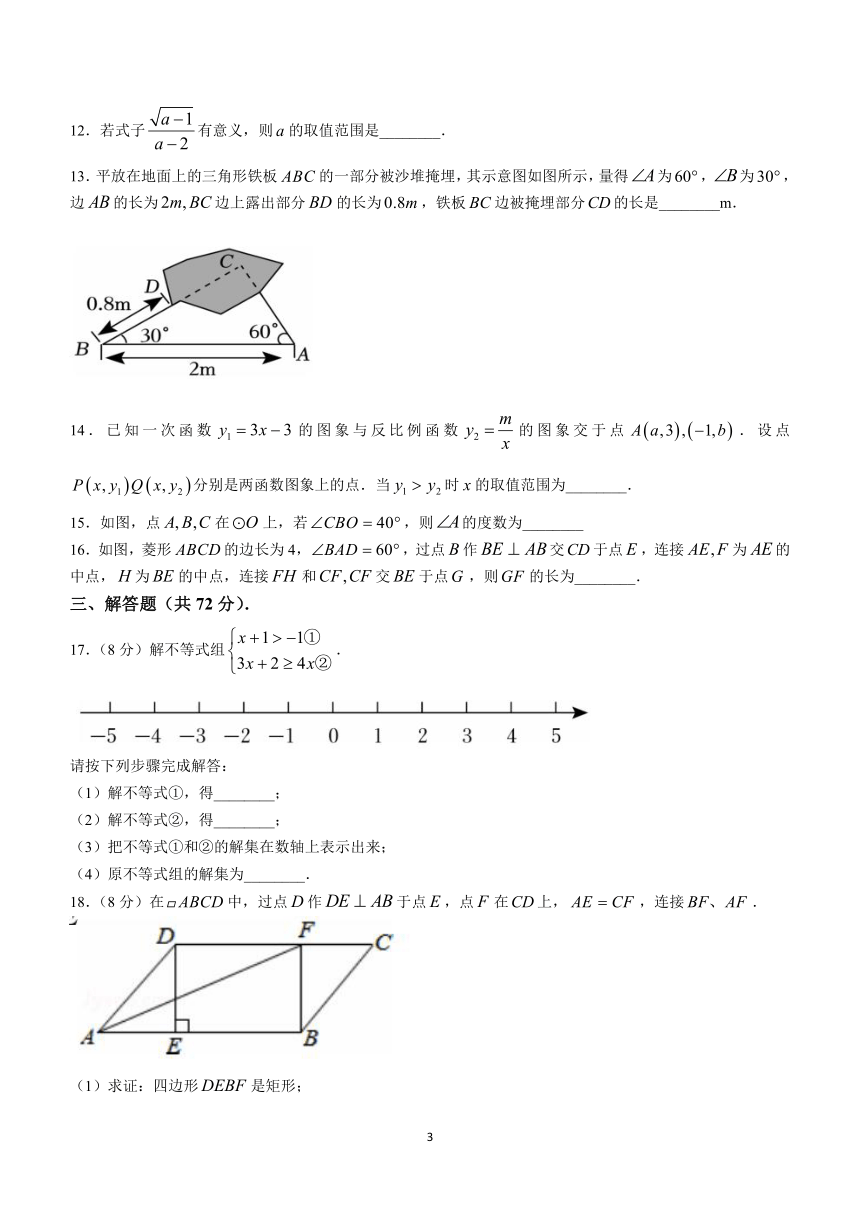
10.在平面直角坐标系中,给出如下定义:为图形上任意一点,如果点到直线的距离等于图形上任意两点距离的最大值时,那么点称为直线的“伴随点”.例如:如图1,已知点在线段上,则点是直线轴的“伴随点”.如图,轴上方有一等边三角形轴,顶点在轴上且在上方,,点是上一点,且点是直线轴的“伴随点”,当点到轴的距离最小时,则等边三角形的边长为( )
A.3 B.2 C.4 D.
二、填空题(每小题3分,共18分)
11.计算:________.
12.若式子有意义,则的取值范围是________.
13.平放在地面上的三角形铁板的一部分被沙堆掩埋,其示意图如图所示,量得为,为,边的长为边上露出部分的长为,铁板边被掩埋部分的长是________m.
14.已知一次函数的图象与反比例函数的图象交于点.设点分别是两函数图象上的点.当时的取值范围为________.
15.如图,点在上,若,则的度数为________
16.如图,菱形的边长为4,,过点作交于点,连接为的中点,为的中点,连接和交于点,则的长为________.
三、解答题(共72分).
17.(8分)解不等式组.
请按下列步骤完成解答:
(1)解不等式①,得________;
(2)解不等式②,得________;
(3)把不等式①和②的解集在数轴上表示出来;
(4)原不等式组的解集为________.
18.(8分)在中,过点作于点,点在上,,连接.
(1)求证:四边形是矩形;
(2)若平分.求的长.
19.(8分)为进一步开展“睡眠管理”工作,某校对部分学生的睡眠情况进行了问卷调查,设每名学生平均每天的睡眠时间为小时,其中的分组情况是:
组: 组: 组: 组: 组:
根据调查结果绘制成两幅不完整的统计图,请根据图中提供的信息,解答下列问题:
(1)本次共调查了________名学生;
(2)补全条形统计图;
(3)若该校有1500名学生,请估计该校睡眠时间不足9小时的学生有多少人?
20.(8分)如图,是由小正方形组成的网格,每个小正方形的顶点叫做格点,的三个顶点都是格点,点与点关于格点所在的直线对称.仅用无刻度直尺在给定网格中按要求画出下列图形,并回答问题.(画图过程用虚线表示,画图结果用实线表示).
(1)直接写出________;
(2)画的高;
(3)在上找一点,使;
(8分)如图,点是的边上一点,以点为圆心,为半径作,与相切于点,交于点,连接并延长交的延长线于点为弧中点.
(1)连接,求证:是的切线;
(2)若,求的长.
22.(10分)北京冬奥会的召开激起了人们对冰雪运动的极大热情,如图是某小型跳台滑雪训练场的横截面示意图,取某一位置的水平线为轴,过跳台终点作水平线的垂线为轴,建立平面直角坐标系.图中的抛物线近似表示滑雪场地上的一座小山坡,小雅从点正上方4米处的点滑出,滑出后沿一段抛物线运动.
(1)当小雅滑到离处的水平距离为6米时,其滑行高度最大,为米.
①求出的值;
②当小雅滑出后离的水平距离为多少米时,她滑行高度与小山坡的竖直距离为米?
(2)小雅若想滑行到坡顶正上方时,与坡顶距离不低于米,请直接写出的取值范围.
23.(10分)(1)如图1,已知和为等腰直角三角形,,,则线段的数量关系为________,线段的位置关系为________.
图1 图2 图3
(2)如图2,已知和中满足,试说明与具有怎样的数量关系.
(3)迁移运用:如图3,已知矩形中有一点,连接,,求的长.
24.(12分)如图,在平面直角坐标系中,为原点,抛物线(为常数)经过点和点.
(Ⅰ)求抛物线的解析式;
(Ⅱ)在抛物线上是否存在一点,使?若存在,请求出点的坐标,若不存在,请说明理由;
(Ⅲ)点为直线下方抛物线上一点,点为轴上一点,当的面积最大时,直接写出的最小值.
一、选择题(每小题3分,共30分)
1.的倒数是( )
A. B. C. D.3
2.2022年,广东省外贸进出口总值再创新高,达到83100亿元,那么“83100”用科学记数法表示为( )
A. B. C. D.
3.下列几何体中,同一个几何体从正面看和从上面看形状图不同的是( )
A. B. C. D.
4.如图,直线,直线与分别交于两点,过点作,垂足为,若,则的度数是( )
A. B. C. D.
5.在九年级体育考试中,某校某班参加仰卧起坐测试的8名女生成绩如下:(单位:次/分):44,45,42,48,46,43,47,45,,则这组数据的众数和中位数分别为( )
A.45,44 B.45,45 C.44,46 D.45,45.5
6.袋子里有8个红球,个白球,3个黑球,每个球除颜色外都相同,从中任意摸出一个球,若摸到红球的可能性最大,则的值不可能是( )
A.1 B.3 C.5 D.10
7.某品牌手机原来每部售价为1999元,经过连续两次降价后,该手机每部售价为1360元,设平均每次降价的百分率为,根据题意,所列方程正确的是( )
A. B. C. D.
8.如图1,点从等边三角形的顶点出发,沿直线运动到三角形内部一点,再从该点沿直线运动到顶点.设点运动的路程为,图2是点运动时随变化的关系图象,则等边三角形的边长为( )
A.6 B.3 C. D.
9.如图,抛物线的图象与轴交于两点与轴交于点,对称轴为,则下列四个结论:①;②;③时,;④.其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
10.在平面直角坐标系中,给出如下定义:为图形上任意一点,如果点到直线的距离等于图形上任意两点距离的最大值时,那么点称为直线的“伴随点”.例如:如图1,已知点在线段上,则点是直线轴的“伴随点”.如图,轴上方有一等边三角形轴,顶点在轴上且在上方,,点是上一点,且点是直线轴的“伴随点”,当点到轴的距离最小时,则等边三角形的边长为( )
A.3 B.2 C.4 D.
二、填空题(每小题3分,共18分)
11.计算:________.
12.若式子有意义,则的取值范围是________.
13.平放在地面上的三角形铁板的一部分被沙堆掩埋,其示意图如图所示,量得为,为,边的长为边上露出部分的长为,铁板边被掩埋部分的长是________m.
14.已知一次函数的图象与反比例函数的图象交于点.设点分别是两函数图象上的点.当时的取值范围为________.
15.如图,点在上,若,则的度数为________
16.如图,菱形的边长为4,,过点作交于点,连接为的中点,为的中点,连接和交于点,则的长为________.
三、解答题(共72分).
17.(8分)解不等式组.
请按下列步骤完成解答:
(1)解不等式①,得________;
(2)解不等式②,得________;
(3)把不等式①和②的解集在数轴上表示出来;
(4)原不等式组的解集为________.
18.(8分)在中,过点作于点,点在上,,连接.
(1)求证:四边形是矩形;
(2)若平分.求的长.
19.(8分)为进一步开展“睡眠管理”工作,某校对部分学生的睡眠情况进行了问卷调查,设每名学生平均每天的睡眠时间为小时,其中的分组情况是:
组: 组: 组: 组: 组:
根据调查结果绘制成两幅不完整的统计图,请根据图中提供的信息,解答下列问题:
(1)本次共调查了________名学生;
(2)补全条形统计图;
(3)若该校有1500名学生,请估计该校睡眠时间不足9小时的学生有多少人?
20.(8分)如图,是由小正方形组成的网格,每个小正方形的顶点叫做格点,的三个顶点都是格点,点与点关于格点所在的直线对称.仅用无刻度直尺在给定网格中按要求画出下列图形,并回答问题.(画图过程用虚线表示,画图结果用实线表示).
(1)直接写出________;
(2)画的高;
(3)在上找一点,使;
(8分)如图,点是的边上一点,以点为圆心,为半径作,与相切于点,交于点,连接并延长交的延长线于点为弧中点.
(1)连接,求证:是的切线;
(2)若,求的长.
22.(10分)北京冬奥会的召开激起了人们对冰雪运动的极大热情,如图是某小型跳台滑雪训练场的横截面示意图,取某一位置的水平线为轴,过跳台终点作水平线的垂线为轴,建立平面直角坐标系.图中的抛物线近似表示滑雪场地上的一座小山坡,小雅从点正上方4米处的点滑出,滑出后沿一段抛物线运动.
(1)当小雅滑到离处的水平距离为6米时,其滑行高度最大,为米.
①求出的值;
②当小雅滑出后离的水平距离为多少米时,她滑行高度与小山坡的竖直距离为米?
(2)小雅若想滑行到坡顶正上方时,与坡顶距离不低于米,请直接写出的取值范围.
23.(10分)(1)如图1,已知和为等腰直角三角形,,,则线段的数量关系为________,线段的位置关系为________.
图1 图2 图3
(2)如图2,已知和中满足,试说明与具有怎样的数量关系.
(3)迁移运用:如图3,已知矩形中有一点,连接,,求的长.
24.(12分)如图,在平面直角坐标系中,为原点,抛物线(为常数)经过点和点.
(Ⅰ)求抛物线的解析式;
(Ⅱ)在抛物线上是否存在一点,使?若存在,请求出点的坐标,若不存在,请说明理由;
(Ⅲ)点为直线下方抛物线上一点,点为轴上一点,当的面积最大时,直接写出的最小值.
同课章节目录
