第七章 平面直角坐标系 单元测试卷(含答案)2023-2024学年人教版数学七年级下册
文档属性
| 名称 | 第七章 平面直角坐标系 单元测试卷(含答案)2023-2024学年人教版数学七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 246.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-04 21:39:51 | ||
图片预览


文档简介
2023-2024学年擢英中学七下坐标轴单元测试卷
一.选择题
1.根据下列表述,能确定具体位置的是( )
A.电影城1号厅6排 B.北京市海淀区
C.北纬31°,东经103° D.南偏西40°
2.在平面直角坐标系中,下列各点位于第四象限的是( )
A.(﹣4,3) B.(4,3) C.(﹣4,﹣3) D.(3,﹣4)
3.若点C在第四象限,距离x轴3个单位长度,距离y轴4个单位长度,则点C的坐标为( )
A.(﹣3,4) B.(3,﹣4) C.(4,﹣3) D.(﹣4,3)
4.若点P(a,b)在第二象限,则M(ab,﹣a)应在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.在平面直角坐标系中,已知线段AB的两个端点分别是A(﹣3,﹣2),B(1,2),将线段AB平移后得到线段A′B′,若点A′坐标为(﹣4,2),则点B′的坐标为( )
A.(0,6) B.(2,2) C.(6,0) D.(5,6)
6.如图,坐标平面上直线L的方程式为x=﹣3,直线M的方程式为y=﹣1,P点的坐标为(a,b).根据图中P点位置判断,下列关系正确的是( )
A.a<﹣3,b>﹣1 B.a<﹣3,b<﹣1 C.a>﹣3,b>﹣1 D.a>﹣5,b<﹣1
7.在平面直角坐标系中,若直线AB经过点(3,﹣4)和(﹣3,4),则直线AB( )
A.平行于x轴 B.平行于y轴 C.经过原点 D.无法确定
8.已知点M(﹣3,﹣2),MN∥y轴,且MN=2,则点N的坐标是( )
A.(﹣3,0) B.(﹣1,﹣2)
C.(﹣3,0)或(﹣3,﹣4) D.(﹣1,﹣2)或(﹣5,﹣2)
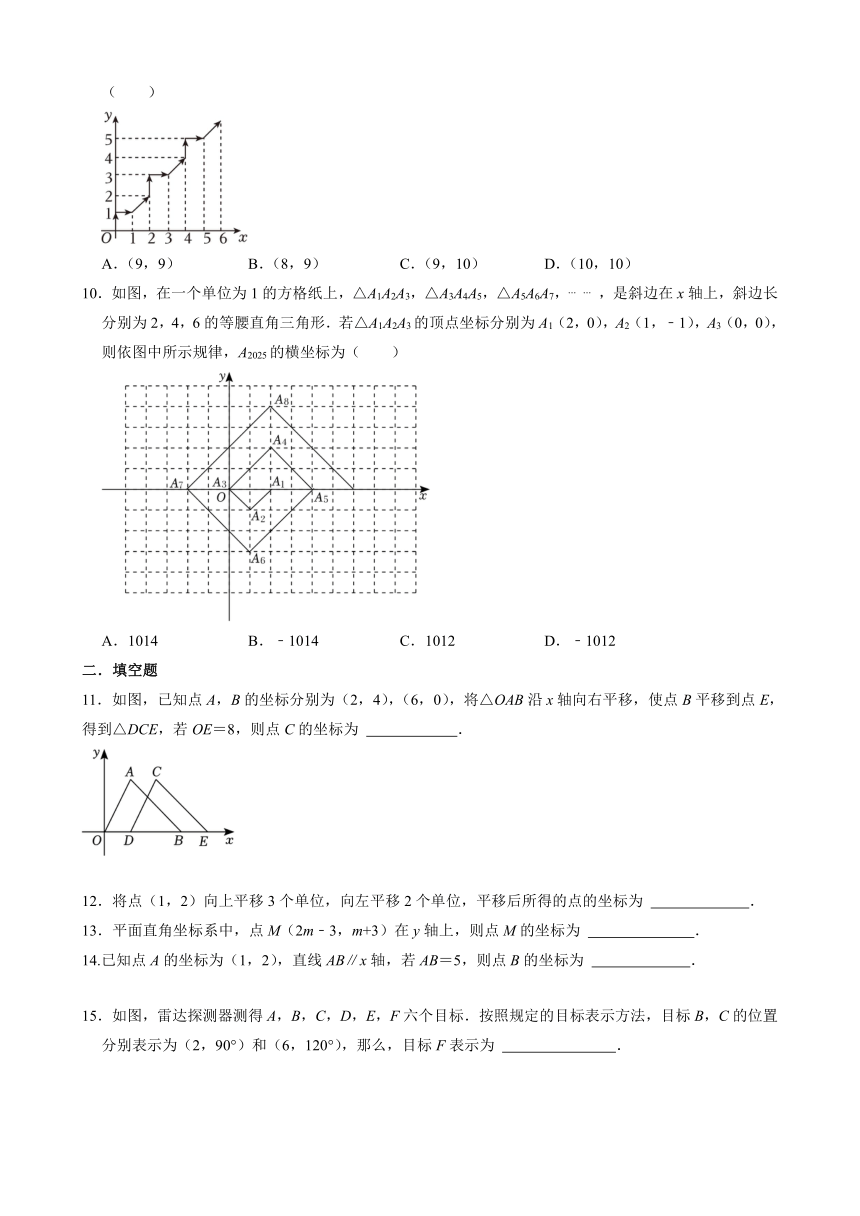
9.在平面直角坐标系中,一个动点按如图所示的方向移动,即(0,0)→(0,1)→(1,1)→(2,2)→(2,3)→(3,3)→(4,4)→……,按此规律,记(0,0)为第1个点,则第15个点的坐标为( )
A.(9,9) B.(8,9) C.(9,10) D.(10,10)
10.如图,在一个单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7, ,是斜边在x轴上,斜边长分别为2,4,6的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2025的横坐标为( )
A.1014 B.﹣1014 C.1012 D.﹣1012
二.填空题
11.如图,已知点A,B的坐标分别为(2,4),(6,0),将△OAB沿x轴向右平移,使点B平移到点E,得到△DCE,若OE=8,则点C的坐标为 .
12.将点(1,2)向上平移3个单位,向左平移2个单位,平移后所得的点的坐标为 .
13.平面直角坐标系中,点M(2m﹣3,m+3)在y轴上,则点M的坐标为 .
14.已知点A的坐标为(1,2),直线AB∥x轴,若AB=5,则点B的坐标为 .
15.如图,雷达探测器测得A,B,C,D,E,F六个目标.按照规定的目标表示方法,目标B,C的位置分别表示为(2,90°)和(6,120°),那么,目标F表示为 .
16.将一组数,,3,,,…,按下面的方法进行排列:
,,3,,,
,,,,,6
…
若的位置记为(1,4),的位置记为(2,2),则这组数中最大的无理数的位置记为 .
三.解答题(共5小题)
17.在平面直角坐标系中有一点P(4x,x﹣3).
(1)若点P在第三象限的角平分线上,求x的值.
(2)若点P位于第四象限,且到两坐标轴的距离之和为9,求点P的坐标.
18.某台阶的一部分如图所示,已知点A的坐标为(0,0),点B的坐标为(1,1).
(1)请建立适当的平面直角坐标系,并写出点C,D,E,F的坐标.
(2)如果该台阶有10级,请求出该台阶的长度和高度.
(3)若平面直角坐标系的单位长度为1m,这10级台阶的宽度都是2m,现要将该台阶铺上地毯,需要多少平方米?
19.如图,△ABC中,任意点P(x0,y0)经平移后对应点为P0(x0+5,y0+3).将△ABC作同样的平移后得到△A1B1C1.
(1)在平面直角坐标系中画出△A1B1C1.
(2)写出点的坐标:A1( , )B1( , )C1( , ).
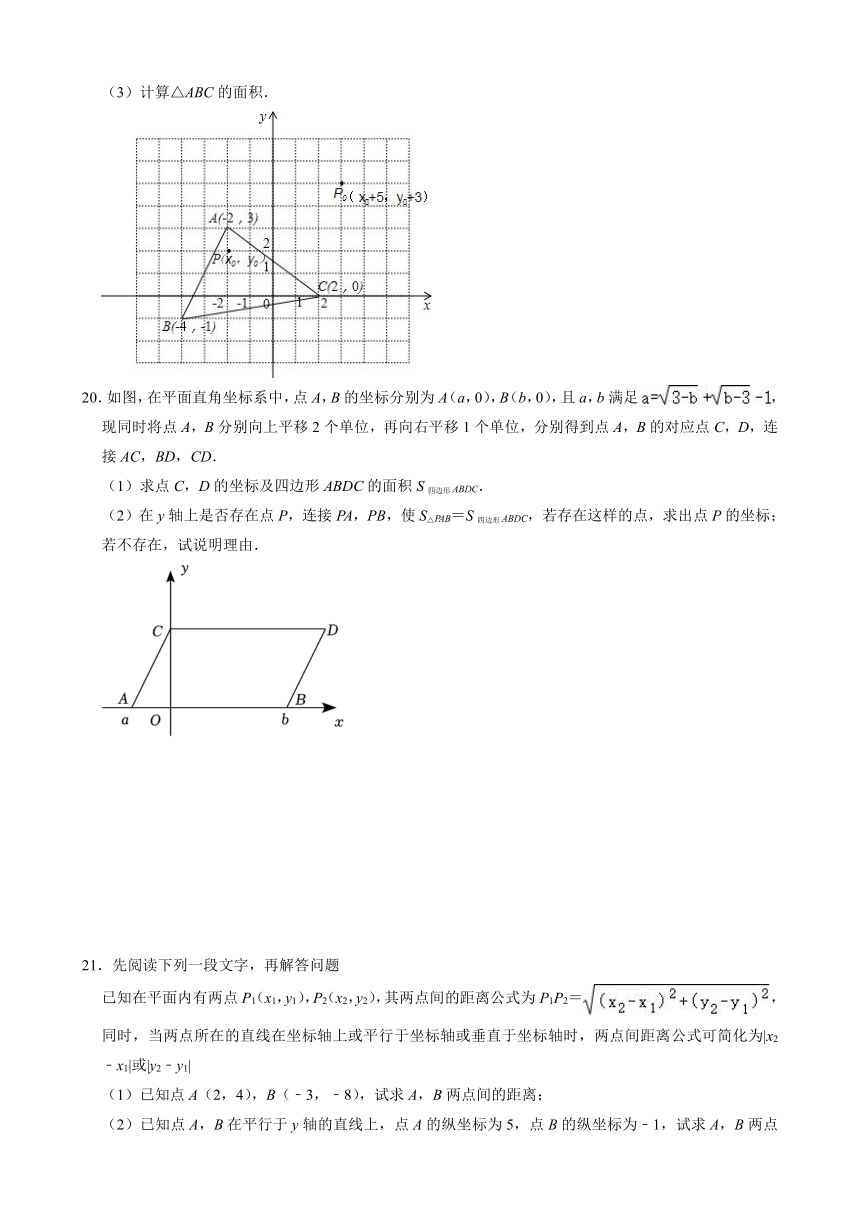
(3)计算△ABC的面积.
20.如图,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足,现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC.
(2)在y轴上是否存在点P,连接PA,PB,使S△PAB=S四边形ABDC,若存在这样的点,求出点P的坐标;若不存在,试说明理由.
21.先阅读下列一段文字,再解答问题
已知在平面内有两点P1(x1,y1),P2(x2,y2),其两点间的距离公式为P1P2=,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|
(1)已知点A(2,4),B(﹣3,﹣8),试求A,B两点间的距离;
(2)已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A,B两点间的距离;
(3)已知点A(0,6)B(﹣3,2),C(3,2),判断线段AB,BC,AC中哪两条是相等的?并说明理由.
2023-2024学年擢英中学坐标轴单元检测卷参考答案
一.选择题
1-5 CDCBA 6-10 ACCAA
10.解:∵图中的各三角形都是等腰直角三角形,斜边长分别为2,4,6,…
∴A1(2,0),A2(1,﹣1),A3(0,0),A4(2,2),A5(4,0),A6(1,﹣3),A7(﹣2,0),A8(2,4),A9(6,0),A10(1,﹣5),A11(﹣4,0),A12(2,6),...
总结得出规律:A4n+1(2n+2,0),A4n+2(1,﹣2n﹣1),A4n+3(﹣2n,0),A4n+4(2,2n+2),
∵2025=4×506+1,
∴点A2023在x轴负半轴上,横坐标为2×506+2=1014.
故选:A.
填空题
11.(4,4).
12.(﹣1,5).
13.(0,4.5).
14.(-6,3)或(4,3)
15.(5,210°).
16.解:由题意可知,一行6个数,被开方数都为3的倍数,
∴共有=30个数,共有30÷6=5行,
∵这组数中最大的无理数为,
∴这组数中最大的无理数的位置记为(5,6).
故答案为:(5,6).
三.解答题(共5小题)
17.解:(1)∵点P(4x,x﹣3)在第三象限的角平分线上,
∴4x=x﹣3,
解得x=﹣1;
(2)∵点P位于第四象限,
∴4x>0,x﹣3<0,
∵到两坐标轴的距离之和为9,
∴4x+3﹣x=9,
解得x=2,
∴4x=8,x﹣3=2﹣3=﹣1,
∴P(8,﹣1).
18.解:(1)建立平面直角坐标系如图所示,
C(2,2),D(3,3),E(4,4),F(5,5);
(2)台阶的长度:1×(10+1)=11,
高度:1×10=10;
∴该台阶的长度为11,高度为10;
(3)∵单位长度为1m,
∴地毯的长度为:(11+10)×1=21(m),
∵台阶的宽度都是2m,
∴地毯的面积为21×2=42(m2),
答:需要42平方米.
19.解:(1)∵P(x0,y0)经平移后对应点为P0(x0+5,y0+3),
∴平移是按照:向右平移5个单位,向上平移3个单位进行的,
所画图形如下:
(2)结合图形可得:A1(3,6),B1(1,2),C1(7,3).
(3)如图:
S△ABC=S矩形DEFB﹣S△ADB﹣S△AEC﹣S△BCF=24﹣4﹣6﹣3=11.
20.解:(1)∵b﹣3≥0且3﹣b≥0,
解得:b=3,
∴a=﹣1,
∴A(﹣1,0),B(3,0),
∵点A,B分别向上平移2个单位,再向右平移1个单位,得到点C,D,
∴C(0,2),D(4,2),
由平移的性质可知四边形ABDC是平行四边形,
∴S四边形ABDC=AB×OC=[3﹣(﹣1)]×2=8;
(2)存在,点P的坐标为(0,4)或(0,﹣4),理由如下:
设点P(0,y),
则,
解得:|y|=4,
故y=±4,点P的坐标为(0,4)或(0,﹣4).
21.解:(1)依据两点间的距离公式,可得AB==13;
(2)当点A,B在平行于y轴的直线上时,AB=|﹣1﹣5|=6;
(3)AB与AC相等.理由:
∵AB==5;
AC==5;
BC=|3﹣(﹣3)|=6.
∴AB=AC.题解析著作权属所有,未经书面同意,不得复制发布日期:2024/4/3 22:56:46;用户:13950789423;邮箱:13950789423;学号:53883552
一.选择题
1.根据下列表述,能确定具体位置的是( )
A.电影城1号厅6排 B.北京市海淀区
C.北纬31°,东经103° D.南偏西40°
2.在平面直角坐标系中,下列各点位于第四象限的是( )
A.(﹣4,3) B.(4,3) C.(﹣4,﹣3) D.(3,﹣4)
3.若点C在第四象限,距离x轴3个单位长度,距离y轴4个单位长度,则点C的坐标为( )
A.(﹣3,4) B.(3,﹣4) C.(4,﹣3) D.(﹣4,3)
4.若点P(a,b)在第二象限,则M(ab,﹣a)应在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.在平面直角坐标系中,已知线段AB的两个端点分别是A(﹣3,﹣2),B(1,2),将线段AB平移后得到线段A′B′,若点A′坐标为(﹣4,2),则点B′的坐标为( )
A.(0,6) B.(2,2) C.(6,0) D.(5,6)
6.如图,坐标平面上直线L的方程式为x=﹣3,直线M的方程式为y=﹣1,P点的坐标为(a,b).根据图中P点位置判断,下列关系正确的是( )
A.a<﹣3,b>﹣1 B.a<﹣3,b<﹣1 C.a>﹣3,b>﹣1 D.a>﹣5,b<﹣1
7.在平面直角坐标系中,若直线AB经过点(3,﹣4)和(﹣3,4),则直线AB( )
A.平行于x轴 B.平行于y轴 C.经过原点 D.无法确定
8.已知点M(﹣3,﹣2),MN∥y轴,且MN=2,则点N的坐标是( )
A.(﹣3,0) B.(﹣1,﹣2)
C.(﹣3,0)或(﹣3,﹣4) D.(﹣1,﹣2)或(﹣5,﹣2)
9.在平面直角坐标系中,一个动点按如图所示的方向移动,即(0,0)→(0,1)→(1,1)→(2,2)→(2,3)→(3,3)→(4,4)→……,按此规律,记(0,0)为第1个点,则第15个点的坐标为( )
A.(9,9) B.(8,9) C.(9,10) D.(10,10)
10.如图,在一个单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7, ,是斜边在x轴上,斜边长分别为2,4,6的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2025的横坐标为( )
A.1014 B.﹣1014 C.1012 D.﹣1012
二.填空题
11.如图,已知点A,B的坐标分别为(2,4),(6,0),将△OAB沿x轴向右平移,使点B平移到点E,得到△DCE,若OE=8,则点C的坐标为 .
12.将点(1,2)向上平移3个单位,向左平移2个单位,平移后所得的点的坐标为 .
13.平面直角坐标系中,点M(2m﹣3,m+3)在y轴上,则点M的坐标为 .
14.已知点A的坐标为(1,2),直线AB∥x轴,若AB=5,则点B的坐标为 .
15.如图,雷达探测器测得A,B,C,D,E,F六个目标.按照规定的目标表示方法,目标B,C的位置分别表示为(2,90°)和(6,120°),那么,目标F表示为 .
16.将一组数,,3,,,…,按下面的方法进行排列:
,,3,,,
,,,,,6
…
若的位置记为(1,4),的位置记为(2,2),则这组数中最大的无理数的位置记为 .
三.解答题(共5小题)
17.在平面直角坐标系中有一点P(4x,x﹣3).
(1)若点P在第三象限的角平分线上,求x的值.
(2)若点P位于第四象限,且到两坐标轴的距离之和为9,求点P的坐标.
18.某台阶的一部分如图所示,已知点A的坐标为(0,0),点B的坐标为(1,1).
(1)请建立适当的平面直角坐标系,并写出点C,D,E,F的坐标.
(2)如果该台阶有10级,请求出该台阶的长度和高度.
(3)若平面直角坐标系的单位长度为1m,这10级台阶的宽度都是2m,现要将该台阶铺上地毯,需要多少平方米?
19.如图,△ABC中,任意点P(x0,y0)经平移后对应点为P0(x0+5,y0+3).将△ABC作同样的平移后得到△A1B1C1.
(1)在平面直角坐标系中画出△A1B1C1.
(2)写出点的坐标:A1( , )B1( , )C1( , ).
(3)计算△ABC的面积.
20.如图,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足,现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC.
(2)在y轴上是否存在点P,连接PA,PB,使S△PAB=S四边形ABDC,若存在这样的点,求出点P的坐标;若不存在,试说明理由.
21.先阅读下列一段文字,再解答问题
已知在平面内有两点P1(x1,y1),P2(x2,y2),其两点间的距离公式为P1P2=,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|
(1)已知点A(2,4),B(﹣3,﹣8),试求A,B两点间的距离;
(2)已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A,B两点间的距离;
(3)已知点A(0,6)B(﹣3,2),C(3,2),判断线段AB,BC,AC中哪两条是相等的?并说明理由.
2023-2024学年擢英中学坐标轴单元检测卷参考答案
一.选择题
1-5 CDCBA 6-10 ACCAA
10.解:∵图中的各三角形都是等腰直角三角形,斜边长分别为2,4,6,…
∴A1(2,0),A2(1,﹣1),A3(0,0),A4(2,2),A5(4,0),A6(1,﹣3),A7(﹣2,0),A8(2,4),A9(6,0),A10(1,﹣5),A11(﹣4,0),A12(2,6),...
总结得出规律:A4n+1(2n+2,0),A4n+2(1,﹣2n﹣1),A4n+3(﹣2n,0),A4n+4(2,2n+2),
∵2025=4×506+1,
∴点A2023在x轴负半轴上,横坐标为2×506+2=1014.
故选:A.
填空题
11.(4,4).
12.(﹣1,5).
13.(0,4.5).
14.(-6,3)或(4,3)
15.(5,210°).
16.解:由题意可知,一行6个数,被开方数都为3的倍数,
∴共有=30个数,共有30÷6=5行,
∵这组数中最大的无理数为,
∴这组数中最大的无理数的位置记为(5,6).
故答案为:(5,6).
三.解答题(共5小题)
17.解:(1)∵点P(4x,x﹣3)在第三象限的角平分线上,
∴4x=x﹣3,
解得x=﹣1;
(2)∵点P位于第四象限,
∴4x>0,x﹣3<0,
∵到两坐标轴的距离之和为9,
∴4x+3﹣x=9,
解得x=2,
∴4x=8,x﹣3=2﹣3=﹣1,
∴P(8,﹣1).
18.解:(1)建立平面直角坐标系如图所示,
C(2,2),D(3,3),E(4,4),F(5,5);
(2)台阶的长度:1×(10+1)=11,
高度:1×10=10;
∴该台阶的长度为11,高度为10;
(3)∵单位长度为1m,
∴地毯的长度为:(11+10)×1=21(m),
∵台阶的宽度都是2m,
∴地毯的面积为21×2=42(m2),
答:需要42平方米.
19.解:(1)∵P(x0,y0)经平移后对应点为P0(x0+5,y0+3),
∴平移是按照:向右平移5个单位,向上平移3个单位进行的,
所画图形如下:
(2)结合图形可得:A1(3,6),B1(1,2),C1(7,3).
(3)如图:
S△ABC=S矩形DEFB﹣S△ADB﹣S△AEC﹣S△BCF=24﹣4﹣6﹣3=11.
20.解:(1)∵b﹣3≥0且3﹣b≥0,
解得:b=3,
∴a=﹣1,
∴A(﹣1,0),B(3,0),
∵点A,B分别向上平移2个单位,再向右平移1个单位,得到点C,D,
∴C(0,2),D(4,2),
由平移的性质可知四边形ABDC是平行四边形,
∴S四边形ABDC=AB×OC=[3﹣(﹣1)]×2=8;
(2)存在,点P的坐标为(0,4)或(0,﹣4),理由如下:
设点P(0,y),
则,
解得:|y|=4,
故y=±4,点P的坐标为(0,4)或(0,﹣4).
21.解:(1)依据两点间的距离公式,可得AB==13;
(2)当点A,B在平行于y轴的直线上时,AB=|﹣1﹣5|=6;
(3)AB与AC相等.理由:
∵AB==5;
AC==5;
BC=|3﹣(﹣3)|=6.
∴AB=AC.题解析著作权属所有,未经书面同意,不得复制发布日期:2024/4/3 22:56:46;用户:13950789423;邮箱:13950789423;学号:53883552
