第七章 平面直角坐标系 点的循环与图形面积 专题讲义-2023-2024学年人教版七年级数学下册 无答案
文档属性
| 名称 | 第七章 平面直角坐标系 点的循环与图形面积 专题讲义-2023-2024学年人教版七年级数学下册 无答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 410.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-04 00:00:00 | ||
图片预览



文档简介
平面直角坐标系专题--点的循环与图形面积问题
平面直角坐标系---规律问题
点的坐标规律
在平面直角坐标系中,点Px2+2, 3在第 象限。
在平面直角坐标系中,点P到x轴的距离是4,到y轴的距离是到x轴距离的2倍,则点P的坐标为 。
点A(a-2,3-2a)在坐标轴上,则a= 。
点A(9-a,2a+3)在一、三象限角平分线上,则a= 。
[总结]
练习:
在平面直角坐标系中,点P x2 2,3在第 象限。
在平面直角坐标系中,点P 5,3x2+3在第 象限。
在平面直角坐标系中,点Px2+5, 2在第 象限。
在平面直角坐标系中,点P到x轴的距离是6,到y轴的距离是到x轴距离的一半,则点P的坐标为 。
在平面直角坐标系中,点P到x轴的距离是2,到y轴的距离是0,则点P的坐标为 。
在平面直角坐标系中,点P到x轴的距离是7,到y轴的距离是到x轴距离的13,则点P的坐标为 。
点A(7-2a,3a+1)在x轴上,则a= ,点A的坐标为 。
点P(4-2x,2x+3)在二、四象限角平分线上,则x= ,点P的坐标为 。
点或图形平移的坐标规律
在平面直角坐标系中,将点P(2,1)向下平移3个单位长度,所得点的坐标是 。
在平面直角坐标系中,将点P(-3,5)先向右平移2个单位长度,再上平移4个单位长度,所得点的坐标是 。
在平面直角坐标系中,点Px+3,4 2x先向左平移1个单位长度,再上下平移2个单位长度后的点在x轴上,则点P的坐标是 。
点M(3,﹣1)经过平移到达点N,N的坐标为(2,1),那么平移方式是( )
A.先向左平移1个单位,再向下平移2个单位 B.先向右平移1个单位,再向下平移2个单位
C.先向左平移1个单位,再向上平移2个单位 D.先向右平移1个单位,再向上平移2个单位
例5.在平面直角坐标系中,线段A′B′是由线段AB经过平移得到的,已知点A(﹣2,1)的对应点为A′(3,1),点B的对应点为B′(4,0),则点B的坐标为( )
A.(9,0) B.(﹣1,0) C.(3,﹣1) D.(﹣3,﹣1)
[总结]
练习:
在平面直角坐标系中,将点P(4,5)先向下平移2个单位长度,再左平移1个单位长度,所得点的坐标是 。
在平面直角坐标系中,将点P(a-2,b)先向下平左移1个单位长度,再下平移1个单位长度,所得点的坐标是 。
在平面直角坐标系中,将点P(-x-2,0)先向右平移-2个单位长度,再上平移1个单位长度,所得点的坐标是 。
在平面直角坐标系中,点Px+3,4 2x先向左平移1个单位长度,再上下平移2个单位长度后的点在x轴上,则点P的坐标是 。
若将点P(1,﹣m)向右平移2个单位后,再向上平移1个单位得到点Q(n,3),则点(m,n)的实际坐标为 。
点A(4,3)经过平移后得点B(6,﹣3),它的平移过程是( )
A.向右平移2个单位后再向下平移6个单位 B.向左平移2个单位后再向下平移2个单位
C.向左平移2个单位后再向上平移6个单位 D.向右平移6个单位后再向上平移2个单位
7.将点P(m+2,2m+1)向左平移1个单位长度到P′,且P′在y轴上,那么P′的坐标是( )
A.(0,﹣1) B.(0,﹣2) C.(0.﹣3) D.(1,1)
8.将点P(m+2,2m+1)向左平移1个单位长度到P′,且P′在y轴上,那么P′的坐标是( )
A.(0,﹣1) B.(0,﹣2) C.(0.﹣3) D.(1,1)
9.线段AB经过平移得到线段CD,其中点A、B的对应点分别为点C、D,这四个点都在如图所示的格点上,那么线段AB上的一点P(a,b)经过平移后,在线段CD上的对应点Q的坐标是( )
(a﹣1,b+3) B.(a﹣1,b﹣3) C.(a+1,b+3) D.(a+1,b﹣3)
点或图形对称的坐标规律
例1.点M(3,1)关于y轴的对称点的坐标为( )
A.(﹣3,1) B.(3,﹣1) C.(﹣3.﹣1) D.(1,3)
例2.在平面直角坐标系中,点M(3,﹣2)与点N关于x轴对称,则点N的坐标是( )
A.(﹣3,﹣2) B.(﹣3,2) C.(3,2) D.(2,﹣3
例3.在直角坐标系中,点A(﹣2,3)的横坐标乘以﹣1,纵坐标不变,得到点B,则A与B的关系是( )
A.关于x轴对称 B.将点A向x轴的负方向平移了1个单位长度
C.关于y轴对称 D.将点A向y轴的负方向平移了1个单位长度
例4.若点(m+3,﹣4)和点(﹣4,n+1)关于x轴对称,则m+n= .
例5.如图,在平面直角坐标系中,△ABC位于第二象限,点B的坐标是(﹣5,2),先把△ABC向右平移4个单位长度得到△A1B1C1,再作与△A1B1C1关于于x轴对称的△A2B2C2,则点B的对应点B2的坐标是( )
A.(﹣3,2) B.(2,﹣3) C.(1,2) D.(﹣1,﹣2)
[总结]
练习:
1.已知点P(3,a)关于x轴的对称点为Q(b,2),则ab=( )
A.6 B.﹣6 C.5 D.﹣5
2.已知点P(1,a)与Q(b,2)关于y轴对称,则a+b的值为( )
A.﹣1 B.1 C.3 D.﹣3
3.点A(a﹣1,5)和点B(2,b﹣1)关于x轴对称,则(a+b)2019= .
4.已知A(2,3),其关于x轴的对称点是B,B关于y轴对称点是C,那么相当于将A经过( )的平移到了C.
A.向左平移4个单位,再向上平移6个单位 B.向左平移4个单位,再向下平移6个单位
C.向右平移4个单位,再向上平移6个单位 D.向下平移6个单位,再向右平移4个单位
特殊规律
【模型】
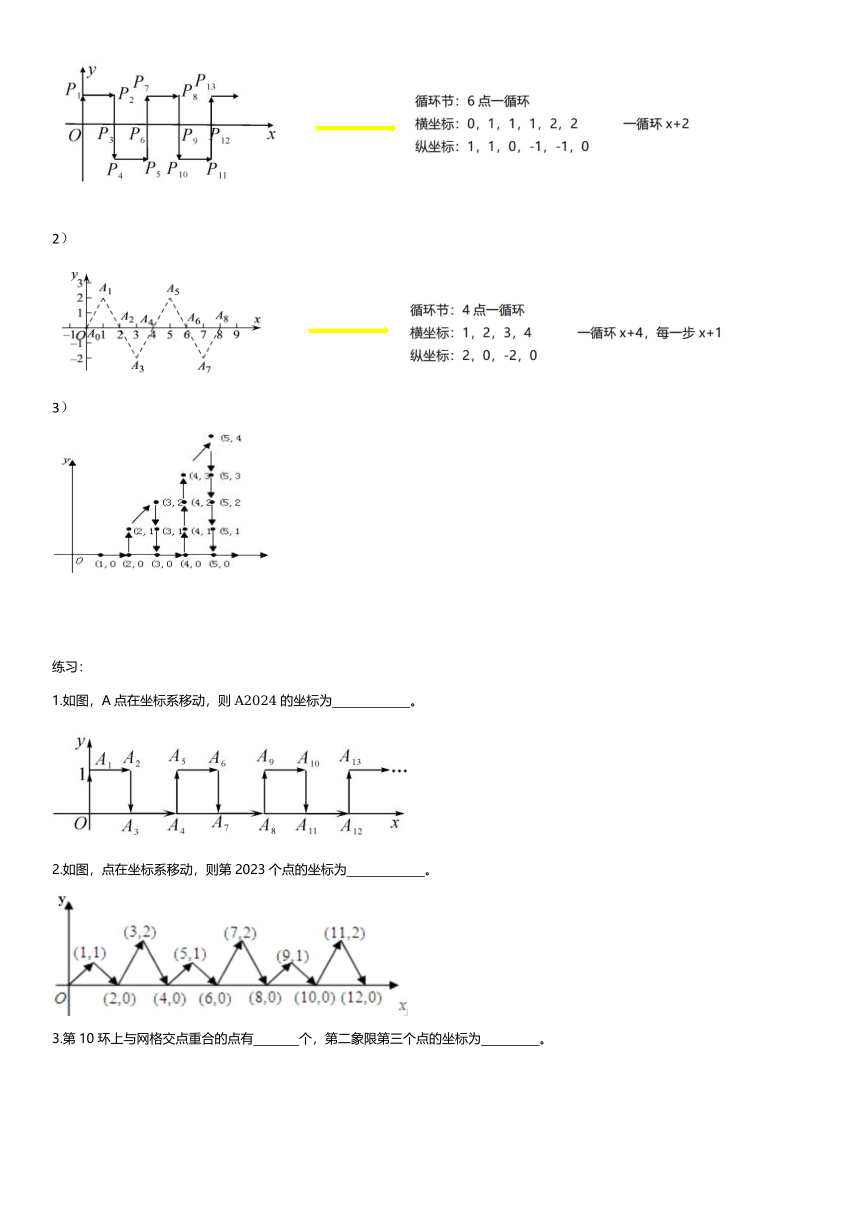
1)
2)
3)
练习:
1.如图,A点在坐标系移动,则A2024的坐标为 。
2.如图,点在坐标系移动,则第2023个点的坐标为 。
3.第10环上与网格交点重合的点有 个,第二象限第三个点的坐标为 。
4.如图,第24个点的坐标为 。
平面直角坐标系---面积问题
例1.如图,在平面直角坐标系中,点A(4,0),B(3,4),C(0,2)
(1)求S四边形ABCO; (2)求S△ABC;
例2.将△ABC向右平移4个单位长度,再向下平移5个单位长度,
(1)作出平移后的△A′B′C′,并写出A′,B′,C′坐标. (2)求出△A′B′C′的面积.
例3.已知:A(4,0),B(3,y),点C在x轴上,AC=5.
(1)直接写出点C的坐标; (2)若S△ABC=10,求点B的坐标.
例4.如图,在平面直角坐标系中,四边形OABC是边长为4的正方形,A点在x轴负半轴上.C点在y轴负半轴上.有一动点P自O点出发,以每秒2个单位长度的速度沿O→A→B→ C→O运动,则何时S△PBC=4并求出此时 P点的坐标.
练习:
1.如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=3.
(1)求点B的坐标,并画出△ABC; (2)求△ABC的面积;
2.如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=3.
(1)求点B的坐标;
(2)求△ABC的面积;
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由.
3.如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=4.
(1)求点B的坐标;
(2)求△ABC的面积;
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为7?若存在,请直接写出点P的坐标;若不存在,请说明理由.
4.在平面直角坐标系中,A(0,2),B(4,0),C(4,3)
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(a,1),试用含a的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使得四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
平面直角坐标系---规律问题
点的坐标规律
在平面直角坐标系中,点Px2+2, 3在第 象限。
在平面直角坐标系中,点P到x轴的距离是4,到y轴的距离是到x轴距离的2倍,则点P的坐标为 。
点A(a-2,3-2a)在坐标轴上,则a= 。
点A(9-a,2a+3)在一、三象限角平分线上,则a= 。
[总结]
练习:
在平面直角坐标系中,点P x2 2,3在第 象限。
在平面直角坐标系中,点P 5,3x2+3在第 象限。
在平面直角坐标系中,点Px2+5, 2在第 象限。
在平面直角坐标系中,点P到x轴的距离是6,到y轴的距离是到x轴距离的一半,则点P的坐标为 。
在平面直角坐标系中,点P到x轴的距离是2,到y轴的距离是0,则点P的坐标为 。
在平面直角坐标系中,点P到x轴的距离是7,到y轴的距离是到x轴距离的13,则点P的坐标为 。
点A(7-2a,3a+1)在x轴上,则a= ,点A的坐标为 。
点P(4-2x,2x+3)在二、四象限角平分线上,则x= ,点P的坐标为 。
点或图形平移的坐标规律
在平面直角坐标系中,将点P(2,1)向下平移3个单位长度,所得点的坐标是 。
在平面直角坐标系中,将点P(-3,5)先向右平移2个单位长度,再上平移4个单位长度,所得点的坐标是 。
在平面直角坐标系中,点Px+3,4 2x先向左平移1个单位长度,再上下平移2个单位长度后的点在x轴上,则点P的坐标是 。
点M(3,﹣1)经过平移到达点N,N的坐标为(2,1),那么平移方式是( )
A.先向左平移1个单位,再向下平移2个单位 B.先向右平移1个单位,再向下平移2个单位
C.先向左平移1个单位,再向上平移2个单位 D.先向右平移1个单位,再向上平移2个单位
例5.在平面直角坐标系中,线段A′B′是由线段AB经过平移得到的,已知点A(﹣2,1)的对应点为A′(3,1),点B的对应点为B′(4,0),则点B的坐标为( )
A.(9,0) B.(﹣1,0) C.(3,﹣1) D.(﹣3,﹣1)
[总结]
练习:
在平面直角坐标系中,将点P(4,5)先向下平移2个单位长度,再左平移1个单位长度,所得点的坐标是 。
在平面直角坐标系中,将点P(a-2,b)先向下平左移1个单位长度,再下平移1个单位长度,所得点的坐标是 。
在平面直角坐标系中,将点P(-x-2,0)先向右平移-2个单位长度,再上平移1个单位长度,所得点的坐标是 。
在平面直角坐标系中,点Px+3,4 2x先向左平移1个单位长度,再上下平移2个单位长度后的点在x轴上,则点P的坐标是 。
若将点P(1,﹣m)向右平移2个单位后,再向上平移1个单位得到点Q(n,3),则点(m,n)的实际坐标为 。
点A(4,3)经过平移后得点B(6,﹣3),它的平移过程是( )
A.向右平移2个单位后再向下平移6个单位 B.向左平移2个单位后再向下平移2个单位
C.向左平移2个单位后再向上平移6个单位 D.向右平移6个单位后再向上平移2个单位
7.将点P(m+2,2m+1)向左平移1个单位长度到P′,且P′在y轴上,那么P′的坐标是( )
A.(0,﹣1) B.(0,﹣2) C.(0.﹣3) D.(1,1)
8.将点P(m+2,2m+1)向左平移1个单位长度到P′,且P′在y轴上,那么P′的坐标是( )
A.(0,﹣1) B.(0,﹣2) C.(0.﹣3) D.(1,1)
9.线段AB经过平移得到线段CD,其中点A、B的对应点分别为点C、D,这四个点都在如图所示的格点上,那么线段AB上的一点P(a,b)经过平移后,在线段CD上的对应点Q的坐标是( )
(a﹣1,b+3) B.(a﹣1,b﹣3) C.(a+1,b+3) D.(a+1,b﹣3)
点或图形对称的坐标规律
例1.点M(3,1)关于y轴的对称点的坐标为( )
A.(﹣3,1) B.(3,﹣1) C.(﹣3.﹣1) D.(1,3)
例2.在平面直角坐标系中,点M(3,﹣2)与点N关于x轴对称,则点N的坐标是( )
A.(﹣3,﹣2) B.(﹣3,2) C.(3,2) D.(2,﹣3
例3.在直角坐标系中,点A(﹣2,3)的横坐标乘以﹣1,纵坐标不变,得到点B,则A与B的关系是( )
A.关于x轴对称 B.将点A向x轴的负方向平移了1个单位长度
C.关于y轴对称 D.将点A向y轴的负方向平移了1个单位长度
例4.若点(m+3,﹣4)和点(﹣4,n+1)关于x轴对称,则m+n= .
例5.如图,在平面直角坐标系中,△ABC位于第二象限,点B的坐标是(﹣5,2),先把△ABC向右平移4个单位长度得到△A1B1C1,再作与△A1B1C1关于于x轴对称的△A2B2C2,则点B的对应点B2的坐标是( )
A.(﹣3,2) B.(2,﹣3) C.(1,2) D.(﹣1,﹣2)
[总结]
练习:
1.已知点P(3,a)关于x轴的对称点为Q(b,2),则ab=( )
A.6 B.﹣6 C.5 D.﹣5
2.已知点P(1,a)与Q(b,2)关于y轴对称,则a+b的值为( )
A.﹣1 B.1 C.3 D.﹣3
3.点A(a﹣1,5)和点B(2,b﹣1)关于x轴对称,则(a+b)2019= .
4.已知A(2,3),其关于x轴的对称点是B,B关于y轴对称点是C,那么相当于将A经过( )的平移到了C.
A.向左平移4个单位,再向上平移6个单位 B.向左平移4个单位,再向下平移6个单位
C.向右平移4个单位,再向上平移6个单位 D.向下平移6个单位,再向右平移4个单位
特殊规律
【模型】
1)
2)
3)
练习:
1.如图,A点在坐标系移动,则A2024的坐标为 。
2.如图,点在坐标系移动,则第2023个点的坐标为 。
3.第10环上与网格交点重合的点有 个,第二象限第三个点的坐标为 。
4.如图,第24个点的坐标为 。
平面直角坐标系---面积问题
例1.如图,在平面直角坐标系中,点A(4,0),B(3,4),C(0,2)
(1)求S四边形ABCO; (2)求S△ABC;
例2.将△ABC向右平移4个单位长度,再向下平移5个单位长度,
(1)作出平移后的△A′B′C′,并写出A′,B′,C′坐标. (2)求出△A′B′C′的面积.
例3.已知:A(4,0),B(3,y),点C在x轴上,AC=5.
(1)直接写出点C的坐标; (2)若S△ABC=10,求点B的坐标.
例4.如图,在平面直角坐标系中,四边形OABC是边长为4的正方形,A点在x轴负半轴上.C点在y轴负半轴上.有一动点P自O点出发,以每秒2个单位长度的速度沿O→A→B→ C→O运动,则何时S△PBC=4并求出此时 P点的坐标.
练习:
1.如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=3.
(1)求点B的坐标,并画出△ABC; (2)求△ABC的面积;
2.如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=3.
(1)求点B的坐标;
(2)求△ABC的面积;
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由.
3.如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=4.
(1)求点B的坐标;
(2)求△ABC的面积;
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为7?若存在,请直接写出点P的坐标;若不存在,请说明理由.
4.在平面直角坐标系中,A(0,2),B(4,0),C(4,3)
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(a,1),试用含a的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使得四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
