初中数学人教版八年级下册 18.2.1.1 矩形的性质 同步训练 含答案
文档属性
| 名称 | 初中数学人教版八年级下册 18.2.1.1 矩形的性质 同步训练 含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 284.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-04 21:49:27 | ||
图片预览



文档简介
第十八章 平行四边形
18.2.1 矩形
第1课时 矩形的性质
一、选择题
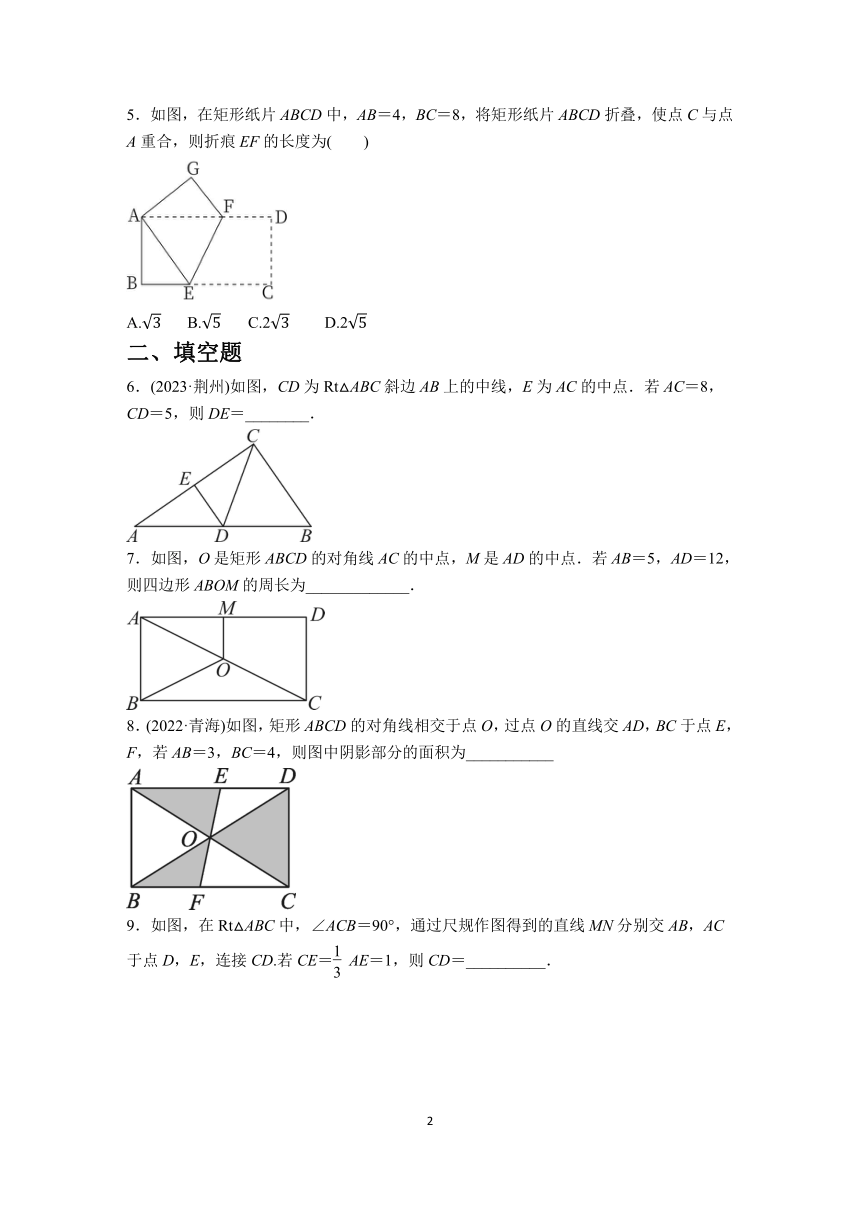
1.(2023·株洲)一技术人员用刻度尺(单位:cm)测量某三角形部件的尺寸.如图所示,已知∠ACB=90°,点D为边AB的中点,点A,B对应的刻度为1,7,则CD=( )
A.3.5 cm B.3 cm C.4.5 cm D.6 cm
2.两个矩形的位置如图所示,若∠1=α,则∠2=( )
A.α-90° B.α-45° C.180°-α D.270°-α
3.(2022·永州)如图,在Rt△ABC中,∠ABC=90°,∠C=60°,点D为边AC的中点,BD=2,则BC的长为( )
A. B.2 C.2 D.4
4.如图,在矩形ABCD中,对角线AC与BD相交于点O.点E,F分别是AB,AO的中点,且AC=8.则EF的长度为( )
A.2 B.4 C.6 D.8
5.如图,在矩形纸片ABCD中,AB=4,BC=8,将矩形纸片ABCD折叠,使点C与点A重合,则折痕EF的长度为( )
A. B. C.2 D.2
二、填空题
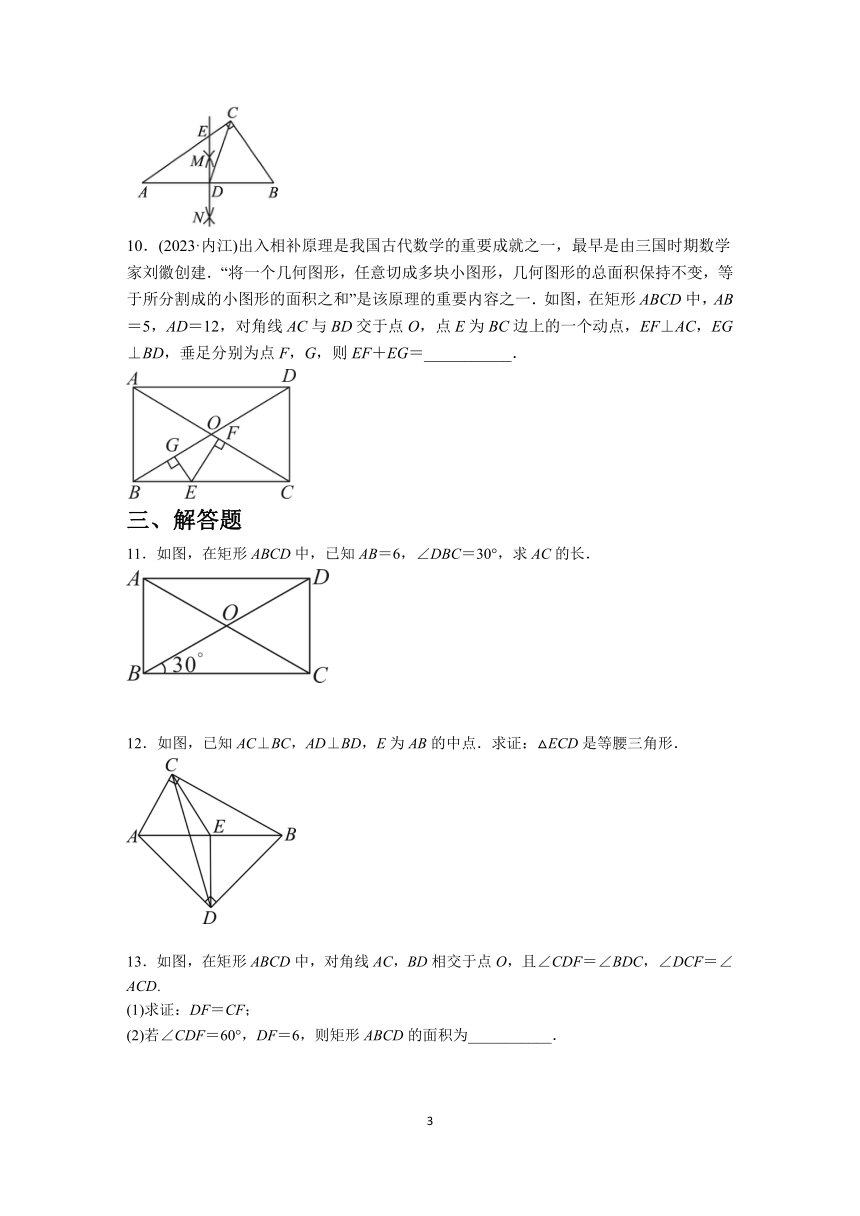
6.(2023·荆州)如图,CD为Rt△ABC斜边AB上的中线,E为AC的中点.若AC=8,CD=5,则DE=________.
7.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点.若AB=5,AD=12,则四边形ABOM的周长为_____________.
8.(2022·青海)如图,矩形ABCD的对角线相交于点O,过点O的直线交AD,BC于点E,F,若AB=3,BC=4,则图中阴影部分的面积为___________
9.如图,在Rt△ABC中,∠ACB=90°,通过尺规作图得到的直线MN分别交AB,AC于点D,E,连接CD.若CE=AE=1,则CD=__________.
10.(2023·内江)出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一.如图,在矩形ABCD中,AB=5,AD=12,对角线AC与BD交于点O,点E为BC边上的一个动点,EF⊥AC,EG⊥BD,垂足分别为点F,G,则EF+EG=___________.
三、解答题
11.如图,在矩形ABCD中,已知AB=6,∠DBC=30°,求AC的长.
12.如图,已知AC⊥BC,AD⊥BD,E为AB的中点.求证:△ECD是等腰三角形.
13.如图,在矩形ABCD中,对角线AC,BD相交于点O,且∠CDF=∠BDC,∠DCF=∠ACD.
(1)求证:DF=CF;
(2)若∠CDF=60°,DF=6,则矩形ABCD的面积为___________.
14.如图,在Rt△ACB中,∠ACB=90°,点M为边AB的中点,点E在线段AM上,EF⊥AC于点F,连接CM,CE.已知∠A=50°,∠ACE=30°.
(1)求证:CE=CM;
(2)若AB=4,求线段FC的长.
15.如图,四边形ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.
(1)求证:四边形AECG是平行四边形;
(2)若AB=4cm,BC=3cm,求线段EF的长.
16.在矩形ABCD中,BC=CD,点E,F分别是边AD,BC上的动点,且AE=CF,连接EF,将矩形ABCD沿EF折叠,点C落在点G处,点D落在点H处.
(1)如图①,当EH与线段BC交于点P时,求证:PE=PF;
(2)如图②,当点P在线段CB的延长线上时,连接AC交EF于点O连接OP.求证:OP⊥EF.
5
参考答案
一、选择题
1.(2023·株洲)一技术人员用刻度尺(单位:cm)测量某三角形部件的尺寸.如图所示,已知∠ACB=90°,点D为边AB的中点,点A,B对应的刻度为1,7,则CD=( B )
A.3.5 cm B.3 cm C.4.5 cm D.6 cm
2.两个矩形的位置如图所示,若∠1=α,则∠2=( C )
A.α-90° B.α-45° C.180°-α D.270°-α
3.(2022·永州)如图,在Rt△ABC中,∠ABC=90°,∠C=60°,点D为边AC的中点,BD=2,则BC的长为( C )
A. B.2 C.2 D.4
4.如图,在矩形ABCD中,对角线AC与BD相交于点O.点E,F分别是AB,AO的中点,且AC=8.则EF的长度为( A )
A.2 B.4 C.6 D.8
5.如图,在矩形纸片ABCD中,AB=4,BC=8,将矩形纸片ABCD折叠,使点C与点A重合,则折痕EF的长度为( D )
A. B. C.2 D.2
二、填空题
6.(2023·荆州)如图,CD为Rt△ABC斜边AB上的中线,E为AC的中点.若AC=8,CD=5,则DE=________.
【答案】3
7.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点.若AB=5,AD=12,则四边形ABOM的周长为_____________.
【答案】20
8.(2022·青海)如图,矩形ABCD的对角线相交于点O,过点O的直线交AD,BC于点E,F,若AB=3,BC=4,则图中阴影部分的面积为___________
【答案】6
9.如图,在Rt△ABC中,∠ACB=90°,通过尺规作图得到的直线MN分别交AB,AC于点D,E,连接CD.若CE=AE=1,则CD=__________.
【答案】
10.(2023·内江)出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一.如图,在矩形ABCD中,AB=5,AD=12,对角线AC与BD交于点O,点E为BC边上的一个动点,EF⊥AC,EG⊥BD,垂足分别为点F,G,则EF+EG=___________.
【答案】
三、解答题
11.如图,在矩形ABCD中,已知AB=6,∠DBC=30°,求AC的长.
解:∵四边形ABCD是矩形,∴CD=AB=6,AC=BD,∠BCD=90°,又∵∠DBC=30°,∴BD=2CD=2×6=12,∴AC=12
12.如图,已知AC⊥BC,AD⊥BD,E为AB的中点.求证:△ECD是等腰三角形.
证明:∵AC⊥BC,AD⊥BD,∴∠ACB=90°,∠ADB=90°.又∵E为AB的中点,∴CE=AB,DE=AB,∴CE=DE,∴△ECD是等腰三角形
13.如图,在矩形ABCD中,对角线AC,BD相交于点O,且∠CDF=∠BDC,∠DCF=∠ACD.
(1)求证:DF=CF;
(2)若∠CDF=60°,DF=6,则矩形ABCD的面积为___________.
解:(1)∵四边形ABCD是矩形,∴OC=AC,OD=BD,AC=BD,∴OC=OD,∴∠ACD=∠BDC,∵∠CDF=∠BDC,∠DCF=∠ACD,∴∠CDF=∠DCF,∴DF=CF
(2)36
14.如图,在Rt△ACB中,∠ACB=90°,点M为边AB的中点,点E在线段AM上,EF⊥AC于点F,连接CM,CE.已知∠A=50°,∠ACE=30°.
(1)求证:CE=CM;
(2)若AB=4,求线段FC的长.
解:(1)∵∠ACB=90°,点M为边AB的中点,∴MC=MA=MB,∴∠MCA=∠A,∠MCB=∠B,∵∠A=50°,∴∠MCA=50°,∠MCB=∠B=40°,∴∠EMC=∠MCB+∠B=80°,∵∠ACE=30°,∠MEC=∠A+∠ACE=80°,∴∠MEC=∠EMC,∴CE=CM
(2)∵AB=4,∴CE=CM=AB=2,∵EF⊥AC,∴∠CFE=90°.在Rt△CEF中,∵∠FCE=30°,∴EF=CE=1.∴CF===
15.如图,四边形ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.
(1)求证:四边形AECG是平行四边形;
(2)若AB=4cm,BC=3cm,求线段EF的长.
(1)证明:在矩形ABCD中,∵AD∥BC,∴∠DAC=∠BCA.由题意,得∠GAH=∠DAC,∠ECF=∠BCA,∴∠GAH=∠ECF,∴AG∥CE.又∵AE∥CG,∴四边形AECG是平行四边形;
(2)解:在Rt△ABC中,∵AB=4,BC=3,∴AC=5.∵CF=CB=3,∴AF=2.在Rt△AEF中,设EF=x,则AE=(4-x).根据勾股定理,得AE2=AF2+EF2,即(4-x)2=22+x2,解得x=,即线段EF的长为cm.
16.在矩形ABCD中,BC=CD,点E,F分别是边AD,BC上的动点,且AE=CF,连接EF,将矩形ABCD沿EF折叠,点C落在点G处,点D落在点H处.
(1)如图①,当EH与线段BC交于点P时,求证:PE=PF;
(2)如图②,当点P在线段CB的延长线上时,连接AC交EF于点O连接OP.求证:OP⊥EF.
证明:(1)四边形ABCD是矩形,∴AD∥BC,∴∠DEF=∠EFB,由翻折的性质得:∠DEF=∠PEF,∴∠PEF=∠PFE,∴PE=PF
(2)四边形ABCD是矩形,AD∥BC,∴∠EAO=∠FCO,∠DEF=∠EFB,由翻折的性质得:∠DEF=∠PEF,∴∠PEF=∠PFE,∴PE=PF,∵AE=CF,∠AOE=∠COF,∴△AEO≌△CFO(AAS),∴OE=OF,∴OP⊥EF
18.2.1 矩形
第1课时 矩形的性质
一、选择题
1.(2023·株洲)一技术人员用刻度尺(单位:cm)测量某三角形部件的尺寸.如图所示,已知∠ACB=90°,点D为边AB的中点,点A,B对应的刻度为1,7,则CD=( )
A.3.5 cm B.3 cm C.4.5 cm D.6 cm
2.两个矩形的位置如图所示,若∠1=α,则∠2=( )
A.α-90° B.α-45° C.180°-α D.270°-α
3.(2022·永州)如图,在Rt△ABC中,∠ABC=90°,∠C=60°,点D为边AC的中点,BD=2,则BC的长为( )
A. B.2 C.2 D.4
4.如图,在矩形ABCD中,对角线AC与BD相交于点O.点E,F分别是AB,AO的中点,且AC=8.则EF的长度为( )
A.2 B.4 C.6 D.8
5.如图,在矩形纸片ABCD中,AB=4,BC=8,将矩形纸片ABCD折叠,使点C与点A重合,则折痕EF的长度为( )
A. B. C.2 D.2
二、填空题
6.(2023·荆州)如图,CD为Rt△ABC斜边AB上的中线,E为AC的中点.若AC=8,CD=5,则DE=________.
7.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点.若AB=5,AD=12,则四边形ABOM的周长为_____________.
8.(2022·青海)如图,矩形ABCD的对角线相交于点O,过点O的直线交AD,BC于点E,F,若AB=3,BC=4,则图中阴影部分的面积为___________
9.如图,在Rt△ABC中,∠ACB=90°,通过尺规作图得到的直线MN分别交AB,AC于点D,E,连接CD.若CE=AE=1,则CD=__________.
10.(2023·内江)出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一.如图,在矩形ABCD中,AB=5,AD=12,对角线AC与BD交于点O,点E为BC边上的一个动点,EF⊥AC,EG⊥BD,垂足分别为点F,G,则EF+EG=___________.
三、解答题
11.如图,在矩形ABCD中,已知AB=6,∠DBC=30°,求AC的长.
12.如图,已知AC⊥BC,AD⊥BD,E为AB的中点.求证:△ECD是等腰三角形.
13.如图,在矩形ABCD中,对角线AC,BD相交于点O,且∠CDF=∠BDC,∠DCF=∠ACD.
(1)求证:DF=CF;
(2)若∠CDF=60°,DF=6,则矩形ABCD的面积为___________.
14.如图,在Rt△ACB中,∠ACB=90°,点M为边AB的中点,点E在线段AM上,EF⊥AC于点F,连接CM,CE.已知∠A=50°,∠ACE=30°.
(1)求证:CE=CM;
(2)若AB=4,求线段FC的长.
15.如图,四边形ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.
(1)求证:四边形AECG是平行四边形;
(2)若AB=4cm,BC=3cm,求线段EF的长.
16.在矩形ABCD中,BC=CD,点E,F分别是边AD,BC上的动点,且AE=CF,连接EF,将矩形ABCD沿EF折叠,点C落在点G处,点D落在点H处.
(1)如图①,当EH与线段BC交于点P时,求证:PE=PF;
(2)如图②,当点P在线段CB的延长线上时,连接AC交EF于点O连接OP.求证:OP⊥EF.
5
参考答案
一、选择题
1.(2023·株洲)一技术人员用刻度尺(单位:cm)测量某三角形部件的尺寸.如图所示,已知∠ACB=90°,点D为边AB的中点,点A,B对应的刻度为1,7,则CD=( B )
A.3.5 cm B.3 cm C.4.5 cm D.6 cm
2.两个矩形的位置如图所示,若∠1=α,则∠2=( C )
A.α-90° B.α-45° C.180°-α D.270°-α
3.(2022·永州)如图,在Rt△ABC中,∠ABC=90°,∠C=60°,点D为边AC的中点,BD=2,则BC的长为( C )
A. B.2 C.2 D.4
4.如图,在矩形ABCD中,对角线AC与BD相交于点O.点E,F分别是AB,AO的中点,且AC=8.则EF的长度为( A )
A.2 B.4 C.6 D.8
5.如图,在矩形纸片ABCD中,AB=4,BC=8,将矩形纸片ABCD折叠,使点C与点A重合,则折痕EF的长度为( D )
A. B. C.2 D.2
二、填空题
6.(2023·荆州)如图,CD为Rt△ABC斜边AB上的中线,E为AC的中点.若AC=8,CD=5,则DE=________.
【答案】3
7.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点.若AB=5,AD=12,则四边形ABOM的周长为_____________.
【答案】20
8.(2022·青海)如图,矩形ABCD的对角线相交于点O,过点O的直线交AD,BC于点E,F,若AB=3,BC=4,则图中阴影部分的面积为___________
【答案】6
9.如图,在Rt△ABC中,∠ACB=90°,通过尺规作图得到的直线MN分别交AB,AC于点D,E,连接CD.若CE=AE=1,则CD=__________.
【答案】
10.(2023·内江)出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一.如图,在矩形ABCD中,AB=5,AD=12,对角线AC与BD交于点O,点E为BC边上的一个动点,EF⊥AC,EG⊥BD,垂足分别为点F,G,则EF+EG=___________.
【答案】
三、解答题
11.如图,在矩形ABCD中,已知AB=6,∠DBC=30°,求AC的长.
解:∵四边形ABCD是矩形,∴CD=AB=6,AC=BD,∠BCD=90°,又∵∠DBC=30°,∴BD=2CD=2×6=12,∴AC=12
12.如图,已知AC⊥BC,AD⊥BD,E为AB的中点.求证:△ECD是等腰三角形.
证明:∵AC⊥BC,AD⊥BD,∴∠ACB=90°,∠ADB=90°.又∵E为AB的中点,∴CE=AB,DE=AB,∴CE=DE,∴△ECD是等腰三角形
13.如图,在矩形ABCD中,对角线AC,BD相交于点O,且∠CDF=∠BDC,∠DCF=∠ACD.
(1)求证:DF=CF;
(2)若∠CDF=60°,DF=6,则矩形ABCD的面积为___________.
解:(1)∵四边形ABCD是矩形,∴OC=AC,OD=BD,AC=BD,∴OC=OD,∴∠ACD=∠BDC,∵∠CDF=∠BDC,∠DCF=∠ACD,∴∠CDF=∠DCF,∴DF=CF
(2)36
14.如图,在Rt△ACB中,∠ACB=90°,点M为边AB的中点,点E在线段AM上,EF⊥AC于点F,连接CM,CE.已知∠A=50°,∠ACE=30°.
(1)求证:CE=CM;
(2)若AB=4,求线段FC的长.
解:(1)∵∠ACB=90°,点M为边AB的中点,∴MC=MA=MB,∴∠MCA=∠A,∠MCB=∠B,∵∠A=50°,∴∠MCA=50°,∠MCB=∠B=40°,∴∠EMC=∠MCB+∠B=80°,∵∠ACE=30°,∠MEC=∠A+∠ACE=80°,∴∠MEC=∠EMC,∴CE=CM
(2)∵AB=4,∴CE=CM=AB=2,∵EF⊥AC,∴∠CFE=90°.在Rt△CEF中,∵∠FCE=30°,∴EF=CE=1.∴CF===
15.如图,四边形ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.
(1)求证:四边形AECG是平行四边形;
(2)若AB=4cm,BC=3cm,求线段EF的长.
(1)证明:在矩形ABCD中,∵AD∥BC,∴∠DAC=∠BCA.由题意,得∠GAH=∠DAC,∠ECF=∠BCA,∴∠GAH=∠ECF,∴AG∥CE.又∵AE∥CG,∴四边形AECG是平行四边形;
(2)解:在Rt△ABC中,∵AB=4,BC=3,∴AC=5.∵CF=CB=3,∴AF=2.在Rt△AEF中,设EF=x,则AE=(4-x).根据勾股定理,得AE2=AF2+EF2,即(4-x)2=22+x2,解得x=,即线段EF的长为cm.
16.在矩形ABCD中,BC=CD,点E,F分别是边AD,BC上的动点,且AE=CF,连接EF,将矩形ABCD沿EF折叠,点C落在点G处,点D落在点H处.
(1)如图①,当EH与线段BC交于点P时,求证:PE=PF;
(2)如图②,当点P在线段CB的延长线上时,连接AC交EF于点O连接OP.求证:OP⊥EF.
证明:(1)四边形ABCD是矩形,∴AD∥BC,∴∠DEF=∠EFB,由翻折的性质得:∠DEF=∠PEF,∴∠PEF=∠PFE,∴PE=PF
(2)四边形ABCD是矩形,AD∥BC,∴∠EAO=∠FCO,∠DEF=∠EFB,由翻折的性质得:∠DEF=∠PEF,∴∠PEF=∠PFE,∴PE=PF,∵AE=CF,∠AOE=∠COF,∴△AEO≌△CFO(AAS),∴OE=OF,∴OP⊥EF
