初中数学人教版八年级下册 18.2.1.2 矩形的判定 同步训练 含答案
文档属性
| 名称 | 初中数学人教版八年级下册 18.2.1.2 矩形的判定 同步训练 含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 266.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-04 00:00:00 | ||
图片预览

文档简介
第十八章 平行四边形
18.2.1 矩形
第2课时 矩形的判定
一、选择题
1.如图,要使平行四边形ABCD成为矩形,需添加的条件是( )
A.AB=BC B.AC⊥BD
C.∠ABC=∠BAD D.∠1=∠2
2.要检验一个四边形的桌面是否为矩形,可行的测量方案是( )
A.测量两条对角线是否相等
B.度量两个角是否是90°
C.测量两条对角线的交点到四个顶点的距离是否相等
D.测量两组对边是否分别相等
3.如图,在平行四边形ABCD中,M,N是BD上两点,BM=DN,连接AM,MC,CN,NA,添加一个条件,使四边形AMCN是矩形,这个条件是( )
A.OM=AC B.MB=MO C.BD⊥AC D.∠AMB=∠CND
4.如图,顺次连接四边形ABCD各边的中点,若得到的四边形EFGH为矩形,则四边形ABCD一定满足( )
A.AB=CD B.AC=BD C.AC⊥BD D.AD∥BC
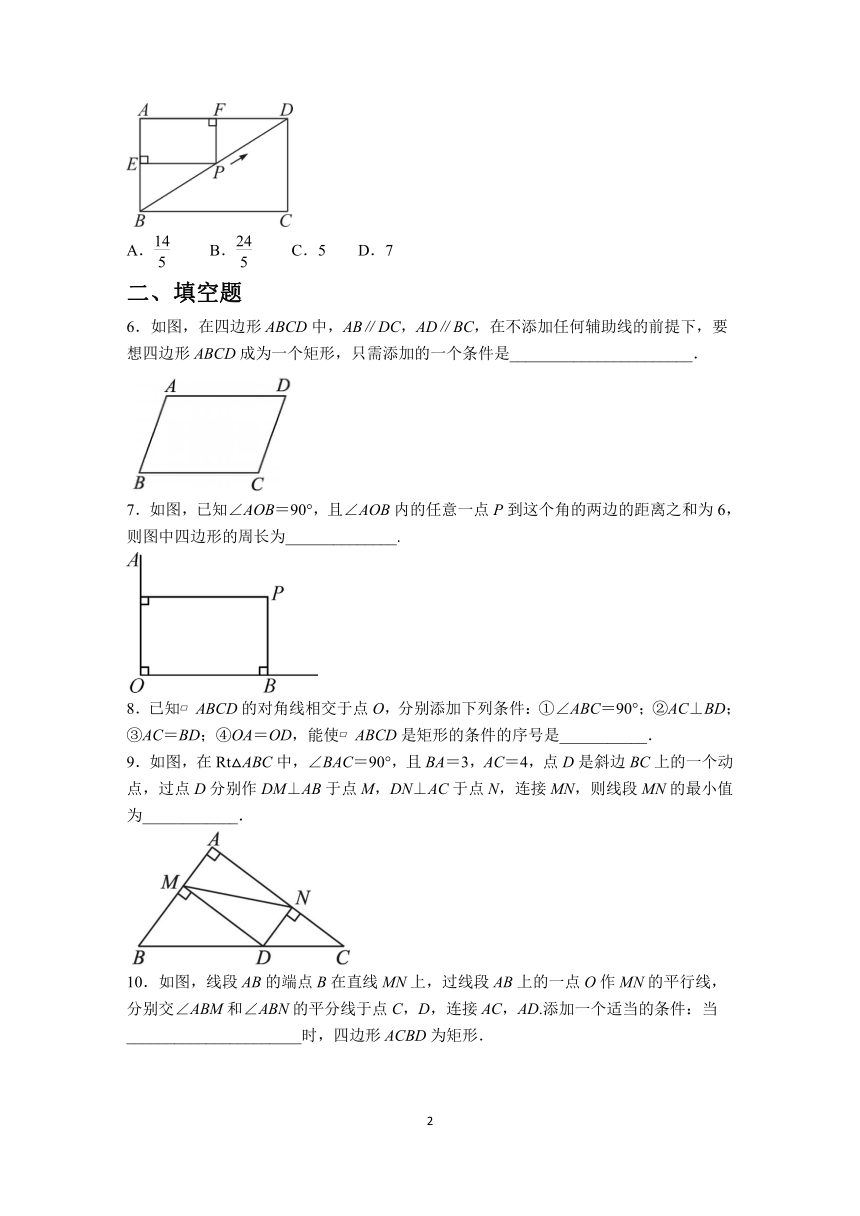
5.(2023·台湾)如图,矩形ABCD中,AB=6,AD=8,且有一点P从B点沿着BD往D点移动,若过P点作AB的垂线交AB于E点,过P点作AD的垂线交AD于F点,则EF的长度最小为多少( )
A. B. C.5 D.7
二、填空题
6.如图,在四边形ABCD中,AB∥DC,AD∥BC,在不添加任何辅助线的前提下,要想四边形ABCD成为一个矩形,只需添加的一个条件是_______________________.
7.如图,已知∠AOB=90°,且∠AOB内的任意一点P到这个角的两边的距离之和为6,则图中四边形的周长为______________.
8.已知 ABCD的对角线相交于点O,分别添加下列条件:①∠ABC=90°;②AC⊥BD;③AC=BD;④OA=OD,能使 ABCD是矩形的条件的序号是___________.
9.如图,在Rt△ABC中,∠BAC=90°,且BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为____________.
10.如图,线段AB的端点B在直线MN上,过线段AB上的一点O作MN的平行线,分别交∠ABM和∠ABN的平分线于点C,D,连接AC,AD.添加一个适当的条件:当______________________时,四边形ACBD为矩形.
11.如图,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3,EF=4,则边AD的长是___________.
三、解答题
12.如图,点E是 ABCD的边AB的中点,且EC=ED.求证:四边形ABCD是矩形
13.如图,矩形ABCD的对角线AC,BD相交于点O,E,F,G,H分别是OA,OB,OC,OD的中点.求证:四边形EFGH是矩形.
14.如图,在 ABCD中,AF,BH,CH,DF分别是∠BAD,∠ABC,∠BCD,∠ADC的平分线.求证:四边形EFGH为矩形.
15.(2023·岳阳)如图,点M在 ABCD的边AD上,BM=CM,请从以下三个选项中①∠1=∠2;②AM=DM;③∠3=∠4,选择一个合适的选项作为已知条件,使 ABCD为矩形.
(1)你添加的条件是______________(填序号);
(2)添加条件后,请证明 ABCD为矩形.、
16.如图,点C是BE的中点,四边形ABCD是平行四边形.
(1)求证:四边形ACED是平行四边形;
(2)如果AB=AE,求证:四边形ACED是矩形.
17.如图,在 ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至点G,使EG=AE,连接CG.
(1)求证:△ABE≌△CDF;
(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.
1
参考答案
一、选择题
1.如图,要使平行四边形ABCD成为矩形,需添加的条件是( C )
A.AB=BC B.AC⊥BD
C.∠ABC=∠BAD D.∠1=∠2
2.要检验一个四边形的桌面是否为矩形,可行的测量方案是( C )
A.测量两条对角线是否相等
B.度量两个角是否是90°
C.测量两条对角线的交点到四个顶点的距离是否相等
D.测量两组对边是否分别相等
3.如图,在平行四边形ABCD中,M,N是BD上两点,BM=DN,连接AM,MC,CN,NA,添加一个条件,使四边形AMCN是矩形,这个条件是( A )
A.OM=AC B.MB=MO C.BD⊥AC D.∠AMB=∠CND
4.如图,顺次连接四边形ABCD各边的中点,若得到的四边形EFGH为矩形,则四边形ABCD一定满足( C )
A.AB=CD B.AC=BD C.AC⊥BD D.AD∥BC
5.(2023·台湾)如图,矩形ABCD中,AB=6,AD=8,且有一点P从B点沿着BD往D点移动,若过P点作AB的垂线交AB于E点,过P点作AD的垂线交AD于F点,则EF的长度最小为多少( B )
A. B. C.5 D.7
二、填空题
6.如图,在四边形ABCD中,AB∥DC,AD∥BC,在不添加任何辅助线的前提下,要想四边形ABCD成为一个矩形,只需添加的一个条件是_______________________.
【答案】∠A=90°(答案不唯一)
7.如图,已知∠AOB=90°,且∠AOB内的任意一点P到这个角的两边的距离之和为6,则图中四边形的周长为______________.
【答案】12
8.已知 ABCD的对角线相交于点O,分别添加下列条件:①∠ABC=90°;②AC⊥BD;③AC=BD;④OA=OD,能使 ABCD是矩形的条件的序号是___________.
【答案】①③④
9.如图,在Rt△ABC中,∠BAC=90°,且BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为____________.
【答案】
10.如图,线段AB的端点B在直线MN上,过线段AB上的一点O作MN的平行线,分别交∠ABM和∠ABN的平分线于点C,D,连接AC,AD.添加一个适当的条件:当______________________时,四边形ACBD为矩形.
【答案】O是AB的中点
11.如图,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3,EF=4,则边AD的长是___________.
【答案】5
三、解答题
12.如图,点E是 ABCD的边AB的中点,且EC=ED.求证:四边形ABCD是矩形
证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC.∵点E是AB的中点,∴AE=BE,又∵ED=EC,∴△AED≌△BEC(SSS),∴∠A=∠B,又∵AD∥BC,∴∠A+∠B=180°,∴∠A=∠B=90°,∴四边形ABCD是矩形
13.如图,矩形ABCD的对角线AC,BD相交于点O,E,F,G,H分别是OA,OB,OC,OD的中点.求证:四边形EFGH是矩形.
证明:∵E是OA的中点,G是OC的中点,∴OE=OA,OG=OC,∵在矩形ABCD中,OA=OC,∴OE=OG,同理OF=OH,∴四边形EFGH是平行四边形,∵OE=OA,OG=OC,∴EG=OE+OG=AC,同理FH=BD,又在矩形ABCD中,AC=BD,∴EG=FH,∴四边形EFGH是矩形
14.如图,在 ABCD中,AF,BH,CH,DF分别是∠BAD,∠ABC,∠BCD,∠ADC的平分线.求证:四边形EFGH为矩形.
证明:∵四边形ABCD是平行四边形,∴∠DAB+∠ADC=180°,∵AF,DF分别平分∠DAB,∠ADC,∴∠FAD=∠BAF=∠DAB,∠ADF=∠CDF=∠ADC,∴∠FAD+∠ADF=∠DAB+∠ADC=(∠DAB+∠ADC)=90°,∴∠AFD=90°,同理可得:∠BHC=∠HEF=90°,∴四边形EFGH是矩形
15.(2023·岳阳)如图,点M在 ABCD的边AD上,BM=CM,请从以下三个选项中①∠1=∠2;②AM=DM;③∠3=∠4,选择一个合适的选项作为已知条件,使 ABCD为矩形.
(1)你添加的条件是______________(填序号);
(2)添加条件后,请证明 ABCD为矩形.、
解:(1)①当∠1=∠2时, ABCD为矩形;②当AM=DM时, ABCD为矩形,故答案为:①(或②)
(2)选择①∠1=∠2,∵四边形ABCD是平行四边形,∴AB∥DC,AB=DC,∴∠A+∠D=180°,在△ABM和DCM中,∴△ABM≌DCM(SAS),∴∠A=∠D=90°,∴ ABCD为矩形
16.如图,点C是BE的中点,四边形ABCD是平行四边形.
(1)求证:四边形ACED是平行四边形;
(2)如果AB=AE,求证:四边形ACED是矩形.
证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC,且AD=BC.∵点C是BE的中点,∴BC=CE,∴AD=CE,∵AD∥CE,∴四边形ACED是平行四边形
(2)∵四边形ABCD是平行四边形,∴AB=DC,∵AB=AE,∴DC=AE,∵四边形ACED是平行四边形,∴四边形ACED是矩形
17.如图,在 ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至点G,使EG=AE,连接CG.
(1)求证:△ABE≌△CDF;
(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.
解:(1)∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,OB=OD,OA=OC,∴∠ABE=∠CDF,∵点E,F分别为OB,OD的中点,∴BE=OB,DF=OD,∴BE=DF,在△ABE和△CDF中,∴△ABE≌△CDF(SAS)
(2)当AC=2AB时,四边形EGCF是矩形.理由如下:由(1)知△ABE≌△CDF,∴AE=CF,∠AEB=∠CFD,∵AE=EG,∠AEB=∠FEG,∴EG=CF,∠FEG=∠DFC,∴EG∥CF,∴四边形EGCF是平行四边形,∵AC=2OA,AC=2AB,∴AB=OA,∵E是OB的中点,∴AG⊥OB,∴∠OEG=90°,∴四边形EGCF是矩形
18.2.1 矩形
第2课时 矩形的判定
一、选择题
1.如图,要使平行四边形ABCD成为矩形,需添加的条件是( )
A.AB=BC B.AC⊥BD
C.∠ABC=∠BAD D.∠1=∠2
2.要检验一个四边形的桌面是否为矩形,可行的测量方案是( )
A.测量两条对角线是否相等
B.度量两个角是否是90°
C.测量两条对角线的交点到四个顶点的距离是否相等
D.测量两组对边是否分别相等
3.如图,在平行四边形ABCD中,M,N是BD上两点,BM=DN,连接AM,MC,CN,NA,添加一个条件,使四边形AMCN是矩形,这个条件是( )
A.OM=AC B.MB=MO C.BD⊥AC D.∠AMB=∠CND
4.如图,顺次连接四边形ABCD各边的中点,若得到的四边形EFGH为矩形,则四边形ABCD一定满足( )
A.AB=CD B.AC=BD C.AC⊥BD D.AD∥BC
5.(2023·台湾)如图,矩形ABCD中,AB=6,AD=8,且有一点P从B点沿着BD往D点移动,若过P点作AB的垂线交AB于E点,过P点作AD的垂线交AD于F点,则EF的长度最小为多少( )
A. B. C.5 D.7
二、填空题
6.如图,在四边形ABCD中,AB∥DC,AD∥BC,在不添加任何辅助线的前提下,要想四边形ABCD成为一个矩形,只需添加的一个条件是_______________________.
7.如图,已知∠AOB=90°,且∠AOB内的任意一点P到这个角的两边的距离之和为6,则图中四边形的周长为______________.
8.已知 ABCD的对角线相交于点O,分别添加下列条件:①∠ABC=90°;②AC⊥BD;③AC=BD;④OA=OD,能使 ABCD是矩形的条件的序号是___________.
9.如图,在Rt△ABC中,∠BAC=90°,且BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为____________.
10.如图,线段AB的端点B在直线MN上,过线段AB上的一点O作MN的平行线,分别交∠ABM和∠ABN的平分线于点C,D,连接AC,AD.添加一个适当的条件:当______________________时,四边形ACBD为矩形.
11.如图,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3,EF=4,则边AD的长是___________.
三、解答题
12.如图,点E是 ABCD的边AB的中点,且EC=ED.求证:四边形ABCD是矩形
13.如图,矩形ABCD的对角线AC,BD相交于点O,E,F,G,H分别是OA,OB,OC,OD的中点.求证:四边形EFGH是矩形.
14.如图,在 ABCD中,AF,BH,CH,DF分别是∠BAD,∠ABC,∠BCD,∠ADC的平分线.求证:四边形EFGH为矩形.
15.(2023·岳阳)如图,点M在 ABCD的边AD上,BM=CM,请从以下三个选项中①∠1=∠2;②AM=DM;③∠3=∠4,选择一个合适的选项作为已知条件,使 ABCD为矩形.
(1)你添加的条件是______________(填序号);
(2)添加条件后,请证明 ABCD为矩形.、
16.如图,点C是BE的中点,四边形ABCD是平行四边形.
(1)求证:四边形ACED是平行四边形;
(2)如果AB=AE,求证:四边形ACED是矩形.
17.如图,在 ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至点G,使EG=AE,连接CG.
(1)求证:△ABE≌△CDF;
(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.
1
参考答案
一、选择题
1.如图,要使平行四边形ABCD成为矩形,需添加的条件是( C )
A.AB=BC B.AC⊥BD
C.∠ABC=∠BAD D.∠1=∠2
2.要检验一个四边形的桌面是否为矩形,可行的测量方案是( C )
A.测量两条对角线是否相等
B.度量两个角是否是90°
C.测量两条对角线的交点到四个顶点的距离是否相等
D.测量两组对边是否分别相等
3.如图,在平行四边形ABCD中,M,N是BD上两点,BM=DN,连接AM,MC,CN,NA,添加一个条件,使四边形AMCN是矩形,这个条件是( A )
A.OM=AC B.MB=MO C.BD⊥AC D.∠AMB=∠CND
4.如图,顺次连接四边形ABCD各边的中点,若得到的四边形EFGH为矩形,则四边形ABCD一定满足( C )
A.AB=CD B.AC=BD C.AC⊥BD D.AD∥BC
5.(2023·台湾)如图,矩形ABCD中,AB=6,AD=8,且有一点P从B点沿着BD往D点移动,若过P点作AB的垂线交AB于E点,过P点作AD的垂线交AD于F点,则EF的长度最小为多少( B )
A. B. C.5 D.7
二、填空题
6.如图,在四边形ABCD中,AB∥DC,AD∥BC,在不添加任何辅助线的前提下,要想四边形ABCD成为一个矩形,只需添加的一个条件是_______________________.
【答案】∠A=90°(答案不唯一)
7.如图,已知∠AOB=90°,且∠AOB内的任意一点P到这个角的两边的距离之和为6,则图中四边形的周长为______________.
【答案】12
8.已知 ABCD的对角线相交于点O,分别添加下列条件:①∠ABC=90°;②AC⊥BD;③AC=BD;④OA=OD,能使 ABCD是矩形的条件的序号是___________.
【答案】①③④
9.如图,在Rt△ABC中,∠BAC=90°,且BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为____________.
【答案】
10.如图,线段AB的端点B在直线MN上,过线段AB上的一点O作MN的平行线,分别交∠ABM和∠ABN的平分线于点C,D,连接AC,AD.添加一个适当的条件:当______________________时,四边形ACBD为矩形.
【答案】O是AB的中点
11.如图,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3,EF=4,则边AD的长是___________.
【答案】5
三、解答题
12.如图,点E是 ABCD的边AB的中点,且EC=ED.求证:四边形ABCD是矩形
证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC.∵点E是AB的中点,∴AE=BE,又∵ED=EC,∴△AED≌△BEC(SSS),∴∠A=∠B,又∵AD∥BC,∴∠A+∠B=180°,∴∠A=∠B=90°,∴四边形ABCD是矩形
13.如图,矩形ABCD的对角线AC,BD相交于点O,E,F,G,H分别是OA,OB,OC,OD的中点.求证:四边形EFGH是矩形.
证明:∵E是OA的中点,G是OC的中点,∴OE=OA,OG=OC,∵在矩形ABCD中,OA=OC,∴OE=OG,同理OF=OH,∴四边形EFGH是平行四边形,∵OE=OA,OG=OC,∴EG=OE+OG=AC,同理FH=BD,又在矩形ABCD中,AC=BD,∴EG=FH,∴四边形EFGH是矩形
14.如图,在 ABCD中,AF,BH,CH,DF分别是∠BAD,∠ABC,∠BCD,∠ADC的平分线.求证:四边形EFGH为矩形.
证明:∵四边形ABCD是平行四边形,∴∠DAB+∠ADC=180°,∵AF,DF分别平分∠DAB,∠ADC,∴∠FAD=∠BAF=∠DAB,∠ADF=∠CDF=∠ADC,∴∠FAD+∠ADF=∠DAB+∠ADC=(∠DAB+∠ADC)=90°,∴∠AFD=90°,同理可得:∠BHC=∠HEF=90°,∴四边形EFGH是矩形
15.(2023·岳阳)如图,点M在 ABCD的边AD上,BM=CM,请从以下三个选项中①∠1=∠2;②AM=DM;③∠3=∠4,选择一个合适的选项作为已知条件,使 ABCD为矩形.
(1)你添加的条件是______________(填序号);
(2)添加条件后,请证明 ABCD为矩形.、
解:(1)①当∠1=∠2时, ABCD为矩形;②当AM=DM时, ABCD为矩形,故答案为:①(或②)
(2)选择①∠1=∠2,∵四边形ABCD是平行四边形,∴AB∥DC,AB=DC,∴∠A+∠D=180°,在△ABM和DCM中,∴△ABM≌DCM(SAS),∴∠A=∠D=90°,∴ ABCD为矩形
16.如图,点C是BE的中点,四边形ABCD是平行四边形.
(1)求证:四边形ACED是平行四边形;
(2)如果AB=AE,求证:四边形ACED是矩形.
证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC,且AD=BC.∵点C是BE的中点,∴BC=CE,∴AD=CE,∵AD∥CE,∴四边形ACED是平行四边形
(2)∵四边形ABCD是平行四边形,∴AB=DC,∵AB=AE,∴DC=AE,∵四边形ACED是平行四边形,∴四边形ACED是矩形
17.如图,在 ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至点G,使EG=AE,连接CG.
(1)求证:△ABE≌△CDF;
(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.
解:(1)∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,OB=OD,OA=OC,∴∠ABE=∠CDF,∵点E,F分别为OB,OD的中点,∴BE=OB,DF=OD,∴BE=DF,在△ABE和△CDF中,∴△ABE≌△CDF(SAS)
(2)当AC=2AB时,四边形EGCF是矩形.理由如下:由(1)知△ABE≌△CDF,∴AE=CF,∠AEB=∠CFD,∵AE=EG,∠AEB=∠FEG,∴EG=CF,∠FEG=∠DFC,∴EG∥CF,∴四边形EGCF是平行四边形,∵AC=2OA,AC=2AB,∴AB=OA,∵E是OB的中点,∴AG⊥OB,∴∠OEG=90°,∴四边形EGCF是矩形
