初中数学人教版八年级下册 18.2.2.1 菱形的性质 同步训练 含答案
文档属性
| 名称 | 初中数学人教版八年级下册 18.2.2.1 菱形的性质 同步训练 含答案 |
|
|
| 格式 | docx | ||
| 文件大小 | 228.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-04 00:00:00 | ||
图片预览

文档简介
第十八章 平行四边形
18.2.2 菱形
第1课时 菱形的性质
一、选择题
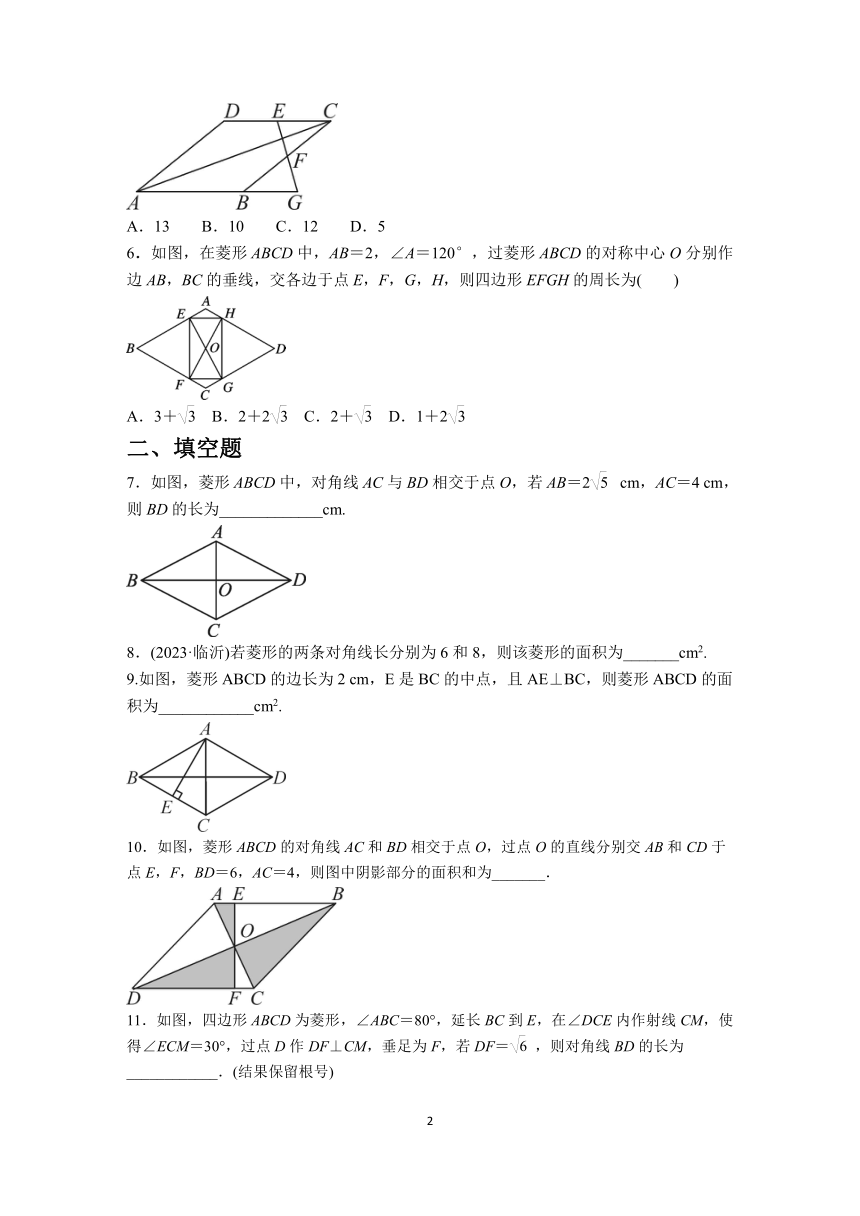
1.关于菱形的性质,以下说法不正确的是( )
A.四条边相等 B.对角线相等
C.对角线互相垂直 D.是轴对称图形
2.如图,菱形ABCD的周长是4 cm,∠ABC=60°,那么这个菱形的对角线AC的长是( )
A.1 cm B.2 cm C.3 cm D.4 cm
3.(2023·乐山)如图,菱形ABCD的对角线AC与BD相交于点O,E为边BC的中点,连接OE.若AC=6,BD=8,则OE=( )
A.2 B. C.3 D.4
4.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为点E,连接DF,则∠CDF等于( )
A.50° B.60° C.70° D.80°
5.如图,菱形ABCD的边长为13,对角线AC=24,点E,F分别是边CD,BC的中点,连接EF并延长与AB的延长线相交于点G,则EG=( )
A.13 B.10 C.12 D.5
6.如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( )
A.3+ B.2+2 C.2+ D.1+2
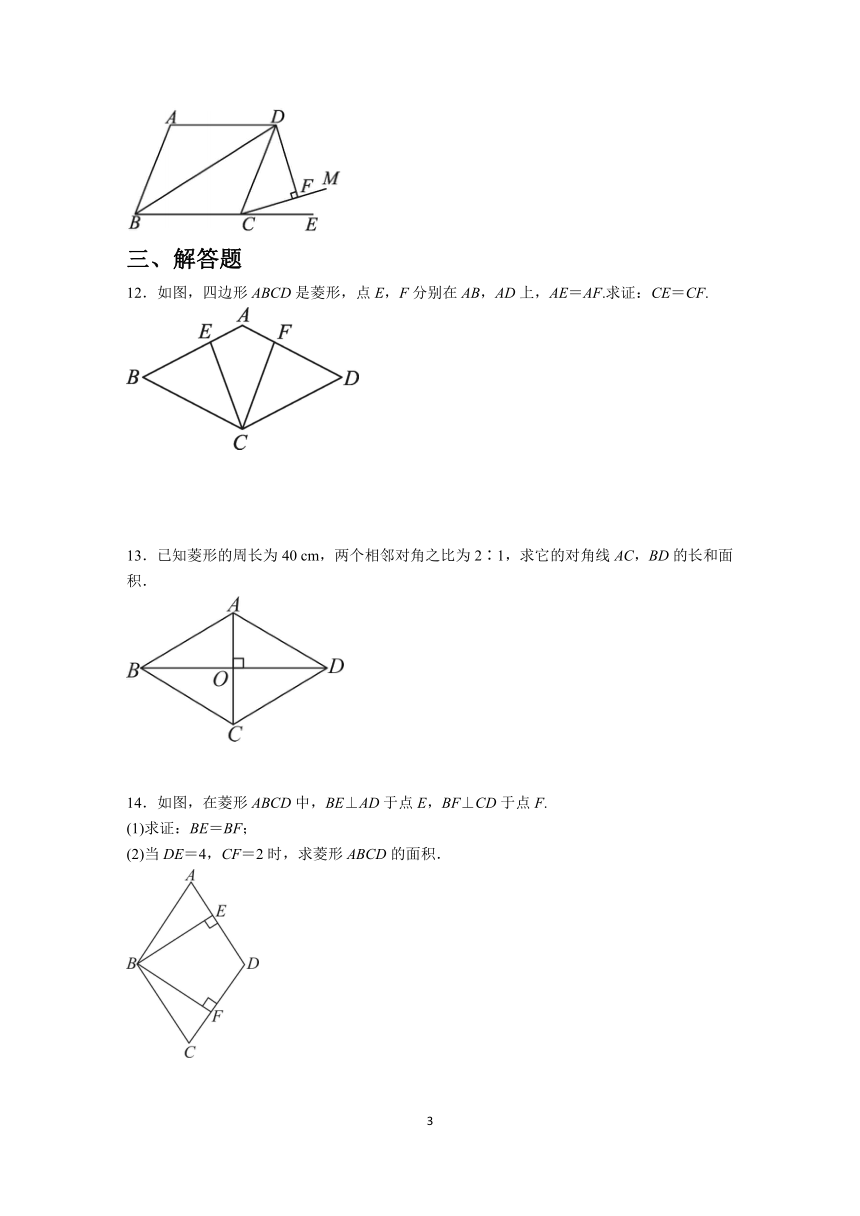
二、填空题
7.如图,菱形ABCD中,对角线AC与BD相交于点O,若AB=2 cm,AC=4 cm,则BD的长为_____________cm.
8.(2023·临沂)若菱形的两条对角线长分别为6和8,则该菱形的面积为_______cm2.
9.如图,菱形ABCD的边长为2 cm,E是BC的中点,且AE⊥BC,则菱形ABCD的面积为____________cm2.
10.如图,菱形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AB和CD于点E,F,BD=6,AC=4,则图中阴影部分的面积和为_______.
11.如图,四边形ABCD为菱形,∠ABC=80°,延长BC到E,在∠DCE内作射线CM,使得∠ECM=30°,过点D作DF⊥CM,垂足为F,若DF=,则对角线BD的长为____________.(结果保留根号)
三、解答题
12.如图,四边形ABCD是菱形,点E,F分别在AB,AD上,AE=AF.求证:CE=CF.
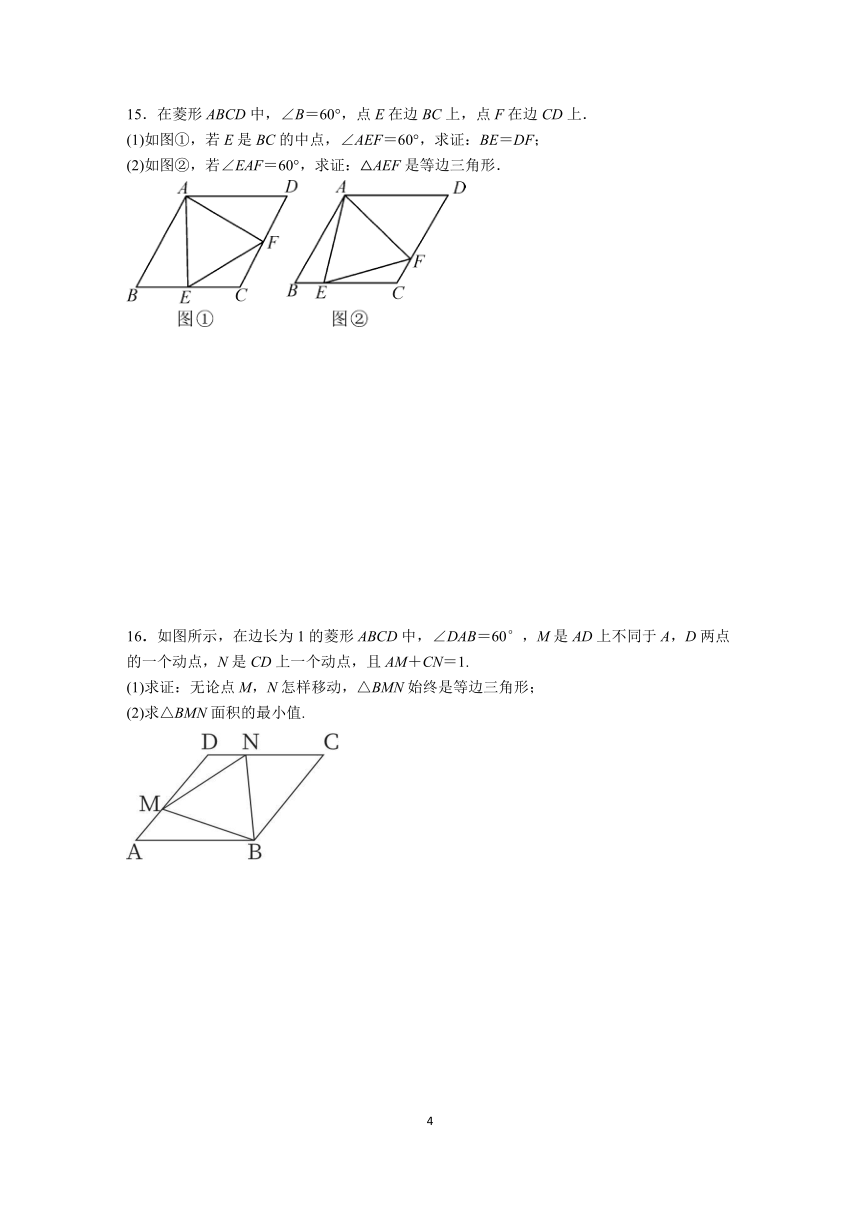
13.已知菱形的周长为40 cm,两个相邻对角之比为2∶1,求它的对角线AC,BD的长和面积.
14.如图,在菱形ABCD中,BE⊥AD于点E,BF⊥CD于点F.
(1)求证:BE=BF;
(2)当DE=4,CF=2时,求菱形ABCD的面积.
15.在菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)如图①,若E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图②,若∠EAF=60°,求证:△AEF是等边三角形.
16.如图所示,在边长为1的菱形ABCD中,∠DAB=60°,M是AD上不同于A,D两点的一个动点,N是CD上一个动点,且AM+CN=1.
(1)求证:无论点M,N怎样移动,△BMN始终是等边三角形;
(2)求△BMN面积的最小值.
1
参考答案
一、选择题
1.关于菱形的性质,以下说法不正确的是( B )
A.四条边相等 B.对角线相等
C.对角线互相垂直 D.是轴对称图形
2.如图,菱形ABCD的周长是4 cm,∠ABC=60°,那么这个菱形的对角线AC的长是( A )
A.1 cm B.2 cm C.3 cm D.4 cm
3.(2023·乐山)如图,菱形ABCD的对角线AC与BD相交于点O,E为边BC的中点,连接OE.若AC=6,BD=8,则OE=( B )
A.2 B. C.3 D.4
4.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为点E,连接DF,则∠CDF等于( B )
A.50° B.60° C.70° D.80°
5.如图,菱形ABCD的边长为13,对角线AC=24,点E,F分别是边CD,BC的中点,连接EF并延长与AB的延长线相交于点G,则EG=( B )
A.13 B.10 C.12 D.5
6.如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( A )
A.3+ B.2+2 C.2+ D.1+2
【解析】如图,连接BD,AC.由题意及菱形的性质证得△BEF,
△DHG,△OEH和△OFG均为等边三角形,由AB=2,∠A=120°,可求得BE=EF=GH=,EH=FG=,∴四边形EFGH的周长为3+.
二、填空题
7.如图,菱形ABCD中,对角线AC与BD相交于点O,若AB=2 cm,AC=4 cm,则BD的长为_____________cm.
【答案】8
8.(2023·临沂)若菱形的两条对角线长分别为6和8,则该菱形的面积为_______cm2.
【答案】24
9.如图,菱形ABCD的边长为2 cm,E是BC的中点,且AE⊥BC,则菱形ABCD的面积为____________cm2.
【答案】2
10.如图,菱形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AB和CD于点E,F,BD=6,AC=4,则图中阴影部分的面积和为_______.
【答案】6
11.如图,四边形ABCD为菱形,∠ABC=80°,延长BC到E,在∠DCE内作射线CM,使得∠ECM=30°,过点D作DF⊥CM,垂足为F,若DF=,则对角线BD的长为____________.(结果保留根号)
【答案】2
三、解答题
12.如图,四边形ABCD是菱形,点E,F分别在AB,AD上,AE=AF.求证:CE=CF.
证明:连接AC,∵四边形ABCD是菱形,∴∠EAC=∠FAC,在△ACE和△ACF中,∴△ACE≌△ACF(SAS),∴CE=CF
13.已知菱形的周长为40 cm,两个相邻对角之比为2∶1,求它的对角线AC,BD的长和面积.
解:∵菱形的周长为40 cm,∴菱形的边长AB=40÷4=10 (cm),∵两个相邻对角之比为2∶1,∴∠ABC=×180°=60°,∴△ABC是等边三角形,∴AC=AB=10 cm,∵菱形对角线AC⊥BD,∴∠BOC=90°.又∵∠OBC=∠ABC=30°,∴OC =BC=×10=5 (cm),∴OB===5(cm),∴BD=2OB=10 cm,∴菱形的面积=AC·BD=×10×10=50(cm2)
14.如图,在菱形ABCD中,BE⊥AD于点E,BF⊥CD于点F.
(1)求证:BE=BF;
(2)当DE=4,CF=2时,求菱形ABCD的面积.
解:(1)∵四边形ABCD是菱形,∴AB=CB,∠A=∠C,∵BE⊥AD,BF⊥CD,∴∠BEA=∠BFC=90°,在△ABE和△CBF中, ∴△ABE≌△CBF (AAS),∴BE=BF
(2)∵DE=4,CF=2,又由(1)可知△ABE≌△CBF,∴AE=CF,∴AD=AE+DE=2+4=6,∵四边形ABCD是菱形,∴BC=CD=AD=6,∵BF⊥CD,∴∠BFC=90°,∴BF===4,∴菱形ABCD的面积为CD·BF=6×4=24
15.在菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)如图①,若E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图②,若∠EAF=60°,求证:△AEF是等边三角形.
证明:(1)连接AC,∵四边形ABCD是菱形,∴AB=BC,∵∠B=60°,∴△ABC是等边三角形,∵点E为BC的中点,∴AE⊥BC,∴∠AEC=90°,∵∠AEF=60°,∴∠FEC=90°-60°=30°,∵∠BCD=180°-∠B=120°,∠BCD+∠EFC+∠FEC=180°,∴∠EFC=30°,∴∠FEC=∠EFC,∴CE=CF,∵BC=CD,∴BC-CE=CD-CF,即BE=DF
(2)连接AC,同(1)可得△ABC是等边三角形,∴AB=AC,∵∠BAE+∠EAC=60°,∠EAF=∠CAF+∠EAC=60°,∴∠BAE=∠CAF,∵四边形ABCD是菱形,∠B=60°,∴∠ACF=∠BCD=∠B=60°,∴△ABE≌△ACF(ASA),∴AE=AF,又∵∠EAF=60°,∴△AEF是等边三角形
16.如图所示,在边长为1的菱形ABCD中,∠DAB=60°,M是AD上不同于A,D两点的一个动点,N是CD上一个动点,且AM+CN=1.
(1)求证:无论点M,N怎样移动,△BMN始终是等边三角形;
(2)求△BMN面积的最小值.
解:(1)连接BD.
易证△ABM≌△DBN,
∴BM=BN,∠MBA=∠NBD.
∵∠MBA+∠DBM=∠ABD=60°,
∴∠NBD+∠DBM=60°,即∠MBN=60°,
∴无论点M,N怎样移动,△BMN始终是等边三角形.
(2)由(1)知△BMN为等边三角形,
∴S△BMN=2.
∵当BM⊥AD时,BM最小,
此时,BM=,则S△BMN=,
∴△BMN面积的最小值为.
18.2.2 菱形
第1课时 菱形的性质
一、选择题
1.关于菱形的性质,以下说法不正确的是( )
A.四条边相等 B.对角线相等
C.对角线互相垂直 D.是轴对称图形
2.如图,菱形ABCD的周长是4 cm,∠ABC=60°,那么这个菱形的对角线AC的长是( )
A.1 cm B.2 cm C.3 cm D.4 cm
3.(2023·乐山)如图,菱形ABCD的对角线AC与BD相交于点O,E为边BC的中点,连接OE.若AC=6,BD=8,则OE=( )
A.2 B. C.3 D.4
4.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为点E,连接DF,则∠CDF等于( )
A.50° B.60° C.70° D.80°
5.如图,菱形ABCD的边长为13,对角线AC=24,点E,F分别是边CD,BC的中点,连接EF并延长与AB的延长线相交于点G,则EG=( )
A.13 B.10 C.12 D.5
6.如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( )
A.3+ B.2+2 C.2+ D.1+2
二、填空题
7.如图,菱形ABCD中,对角线AC与BD相交于点O,若AB=2 cm,AC=4 cm,则BD的长为_____________cm.
8.(2023·临沂)若菱形的两条对角线长分别为6和8,则该菱形的面积为_______cm2.
9.如图,菱形ABCD的边长为2 cm,E是BC的中点,且AE⊥BC,则菱形ABCD的面积为____________cm2.
10.如图,菱形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AB和CD于点E,F,BD=6,AC=4,则图中阴影部分的面积和为_______.
11.如图,四边形ABCD为菱形,∠ABC=80°,延长BC到E,在∠DCE内作射线CM,使得∠ECM=30°,过点D作DF⊥CM,垂足为F,若DF=,则对角线BD的长为____________.(结果保留根号)
三、解答题
12.如图,四边形ABCD是菱形,点E,F分别在AB,AD上,AE=AF.求证:CE=CF.
13.已知菱形的周长为40 cm,两个相邻对角之比为2∶1,求它的对角线AC,BD的长和面积.
14.如图,在菱形ABCD中,BE⊥AD于点E,BF⊥CD于点F.
(1)求证:BE=BF;
(2)当DE=4,CF=2时,求菱形ABCD的面积.
15.在菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)如图①,若E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图②,若∠EAF=60°,求证:△AEF是等边三角形.
16.如图所示,在边长为1的菱形ABCD中,∠DAB=60°,M是AD上不同于A,D两点的一个动点,N是CD上一个动点,且AM+CN=1.
(1)求证:无论点M,N怎样移动,△BMN始终是等边三角形;
(2)求△BMN面积的最小值.
1
参考答案
一、选择题
1.关于菱形的性质,以下说法不正确的是( B )
A.四条边相等 B.对角线相等
C.对角线互相垂直 D.是轴对称图形
2.如图,菱形ABCD的周长是4 cm,∠ABC=60°,那么这个菱形的对角线AC的长是( A )
A.1 cm B.2 cm C.3 cm D.4 cm
3.(2023·乐山)如图,菱形ABCD的对角线AC与BD相交于点O,E为边BC的中点,连接OE.若AC=6,BD=8,则OE=( B )
A.2 B. C.3 D.4
4.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为点E,连接DF,则∠CDF等于( B )
A.50° B.60° C.70° D.80°
5.如图,菱形ABCD的边长为13,对角线AC=24,点E,F分别是边CD,BC的中点,连接EF并延长与AB的延长线相交于点G,则EG=( B )
A.13 B.10 C.12 D.5
6.如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( A )
A.3+ B.2+2 C.2+ D.1+2
【解析】如图,连接BD,AC.由题意及菱形的性质证得△BEF,
△DHG,△OEH和△OFG均为等边三角形,由AB=2,∠A=120°,可求得BE=EF=GH=,EH=FG=,∴四边形EFGH的周长为3+.
二、填空题
7.如图,菱形ABCD中,对角线AC与BD相交于点O,若AB=2 cm,AC=4 cm,则BD的长为_____________cm.
【答案】8
8.(2023·临沂)若菱形的两条对角线长分别为6和8,则该菱形的面积为_______cm2.
【答案】24
9.如图,菱形ABCD的边长为2 cm,E是BC的中点,且AE⊥BC,则菱形ABCD的面积为____________cm2.
【答案】2
10.如图,菱形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AB和CD于点E,F,BD=6,AC=4,则图中阴影部分的面积和为_______.
【答案】6
11.如图,四边形ABCD为菱形,∠ABC=80°,延长BC到E,在∠DCE内作射线CM,使得∠ECM=30°,过点D作DF⊥CM,垂足为F,若DF=,则对角线BD的长为____________.(结果保留根号)
【答案】2
三、解答题
12.如图,四边形ABCD是菱形,点E,F分别在AB,AD上,AE=AF.求证:CE=CF.
证明:连接AC,∵四边形ABCD是菱形,∴∠EAC=∠FAC,在△ACE和△ACF中,∴△ACE≌△ACF(SAS),∴CE=CF
13.已知菱形的周长为40 cm,两个相邻对角之比为2∶1,求它的对角线AC,BD的长和面积.
解:∵菱形的周长为40 cm,∴菱形的边长AB=40÷4=10 (cm),∵两个相邻对角之比为2∶1,∴∠ABC=×180°=60°,∴△ABC是等边三角形,∴AC=AB=10 cm,∵菱形对角线AC⊥BD,∴∠BOC=90°.又∵∠OBC=∠ABC=30°,∴OC =BC=×10=5 (cm),∴OB===5(cm),∴BD=2OB=10 cm,∴菱形的面积=AC·BD=×10×10=50(cm2)
14.如图,在菱形ABCD中,BE⊥AD于点E,BF⊥CD于点F.
(1)求证:BE=BF;
(2)当DE=4,CF=2时,求菱形ABCD的面积.
解:(1)∵四边形ABCD是菱形,∴AB=CB,∠A=∠C,∵BE⊥AD,BF⊥CD,∴∠BEA=∠BFC=90°,在△ABE和△CBF中, ∴△ABE≌△CBF (AAS),∴BE=BF
(2)∵DE=4,CF=2,又由(1)可知△ABE≌△CBF,∴AE=CF,∴AD=AE+DE=2+4=6,∵四边形ABCD是菱形,∴BC=CD=AD=6,∵BF⊥CD,∴∠BFC=90°,∴BF===4,∴菱形ABCD的面积为CD·BF=6×4=24
15.在菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)如图①,若E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图②,若∠EAF=60°,求证:△AEF是等边三角形.
证明:(1)连接AC,∵四边形ABCD是菱形,∴AB=BC,∵∠B=60°,∴△ABC是等边三角形,∵点E为BC的中点,∴AE⊥BC,∴∠AEC=90°,∵∠AEF=60°,∴∠FEC=90°-60°=30°,∵∠BCD=180°-∠B=120°,∠BCD+∠EFC+∠FEC=180°,∴∠EFC=30°,∴∠FEC=∠EFC,∴CE=CF,∵BC=CD,∴BC-CE=CD-CF,即BE=DF
(2)连接AC,同(1)可得△ABC是等边三角形,∴AB=AC,∵∠BAE+∠EAC=60°,∠EAF=∠CAF+∠EAC=60°,∴∠BAE=∠CAF,∵四边形ABCD是菱形,∠B=60°,∴∠ACF=∠BCD=∠B=60°,∴△ABE≌△ACF(ASA),∴AE=AF,又∵∠EAF=60°,∴△AEF是等边三角形
16.如图所示,在边长为1的菱形ABCD中,∠DAB=60°,M是AD上不同于A,D两点的一个动点,N是CD上一个动点,且AM+CN=1.
(1)求证:无论点M,N怎样移动,△BMN始终是等边三角形;
(2)求△BMN面积的最小值.
解:(1)连接BD.
易证△ABM≌△DBN,
∴BM=BN,∠MBA=∠NBD.
∵∠MBA+∠DBM=∠ABD=60°,
∴∠NBD+∠DBM=60°,即∠MBN=60°,
∴无论点M,N怎样移动,△BMN始终是等边三角形.
(2)由(1)知△BMN为等边三角形,
∴S△BMN=2.
∵当BM⊥AD时,BM最小,
此时,BM=,则S△BMN=,
∴△BMN面积的最小值为.
