人教版八年级下册18.2.3 正方形 同步训练(含答案)
文档属性
| 名称 | 人教版八年级下册18.2.3 正方形 同步训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 206.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-04 21:56:27 | ||
图片预览


文档简介
第十八章 平行四边形
18.2.3 正方形
一、选择题
1.正方形具有而菱形不一定具有的性质是( )
A.对角线互相平分 B.对角线相等 C.对角线互相垂直 D.对角线平分一组对角
2.若正方形的一条对角线的长为4,则这个正方形的面积是( )
A.8 B.4 C.8 D.16
3.如图,在正方形ABCD中,对角线AC,BD相交于点O,则图中的等腰直角三角形有( )
A.4个 B.6个 C.8个 D.10个
4.如图,在正方形ABCD的外侧作等边三角形ABE,则∠BED的度数为( )
A.15° B.35° C.45° D.55°
5.下列命题,其中是真命题的是( )
A.对角线互相垂直的四边形是平行四边形 B.有一个角是直角的四边形是矩形
C.对角线互相平分的四边形是菱形 D.对角线互相垂直的矩形是正方形
6.如图,O为正方形ABCD对角线AC的中点,△ACE为等边三角形.若AB=4,则OE的长为( )
A. B.2 C.4 D.4
7.如图,在边长为2的等边三角形ABC的外侧作正方形ABED,过点D作DF⊥BC,垂足为F,则DF的长为( )
A.2+2 B.5- C.3- D.+1
二、填空题
8.(2023·怀化)如图,点P是正方形ABCD的对角线AC上的一点,PE⊥AD于点E,PE=3.则点P到直线AB的距离为________.
9.(2022·无锡)如图,正方形ABCD的边长为8,点E是CD的中点,HG垂直平分AE且分别交AE,BC于点H,G,则BG=_____________.
10.(2023·哈尔滨)如图,在正方形ABCD中,点E在CD上,连接AE,BE,F为BE的中点,连接CF,若CF=,=,则AE的长为__________
11.如图,正方形ABCD的边长为8,点M在DC上且DM=2,N是AC上的一动点,则DN+MN的最小值是 .
三、解答题
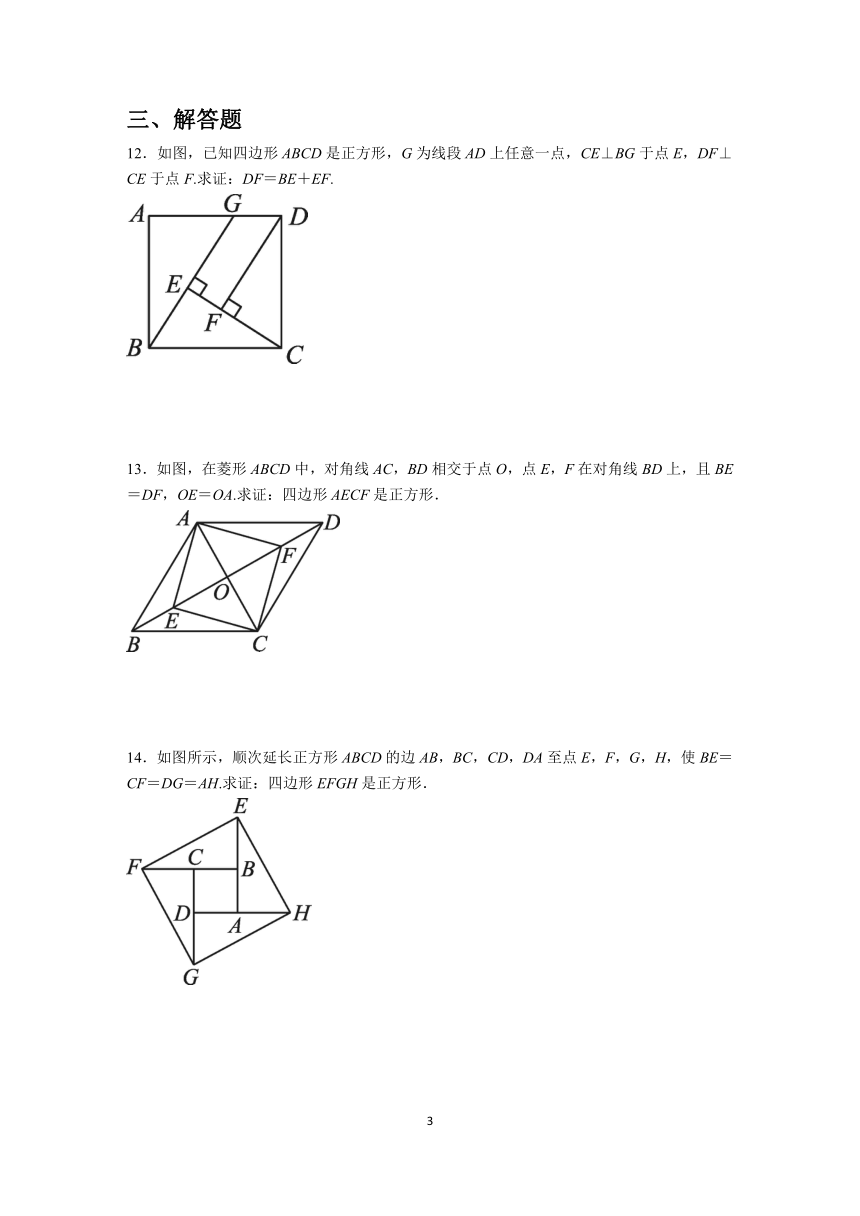
12.如图,已知四边形ABCD是正方形,G为线段AD上任意一点,CE⊥BG于点E,DF⊥CE于点F.求证:DF=BE+EF.
13.如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=DF,OE=OA.求证:四边形AECF是正方形.
14.如图所示,顺次延长正方形ABCD的边AB,BC,CD,DA至点E,F,G,H,使BE=CF=DG=AH.求证:四边形EFGH是正方形.
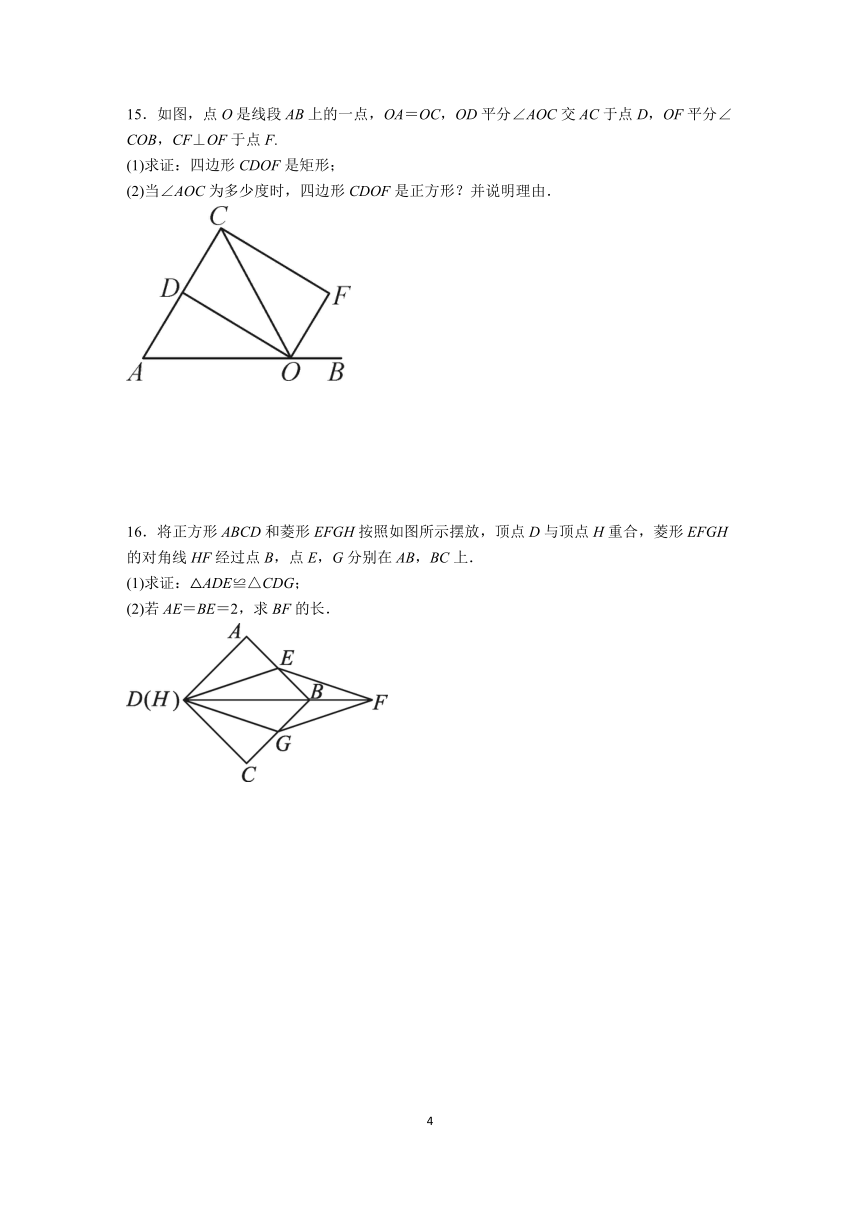
15.如图,点O是线段AB上的一点,OA=OC,OD平分∠AOC交AC于点D,OF平分∠COB,CF⊥OF于点F.
(1)求证:四边形CDOF是矩形;
(2)当∠AOC为多少度时,四边形CDOF是正方形?并说明理由.
16.将正方形ABCD和菱形EFGH按照如图所示摆放,顶点D与顶点H重合,菱形EFGH的对角线HF经过点B,点E,G分别在AB,BC上.
(1)求证:△ADE≌△CDG;
(2)若AE=BE=2,求BF的长.
1
参考答案
一、选择题
1.正方形具有而菱形不一定具有的性质是( B )
A.对角线互相平分 B.对角线相等 C.对角线互相垂直 D.对角线平分一组对角
2.若正方形的一条对角线的长为4,则这个正方形的面积是( A )
A.8 B.4 C.8 D.16
3.如图,在正方形ABCD中,对角线AC,BD相交于点O,则图中的等腰直角三角形有( C )
A.4个 B.6个 C.8个 D.10个
4.如图,在正方形ABCD的外侧作等边三角形ABE,则∠BED的度数为( C )
A.15° B.35° C.45° D.55°
5.下列命题,其中是真命题的是( D )
A.对角线互相垂直的四边形是平行四边形 B.有一个角是直角的四边形是矩形
C.对角线互相平分的四边形是菱形 D.对角线互相垂直的矩形是正方形
6.如图,O为正方形ABCD对角线AC的中点,△ACE为等边三角形.若AB=4,则OE的长为( B )
A. B.2 C.4 D.4
7.如图,在边长为2的等边三角形ABC的外侧作正方形ABED,过点D作DF⊥BC,垂足为F,则DF的长为( D )
A.2+2 B.5- C.3- D.+1
二、填空题
8.(2023·怀化)如图,点P是正方形ABCD的对角线AC上的一点,PE⊥AD于点E,PE=3.则点P到直线AB的距离为________.
【答案】3
9.(2022·无锡)如图,正方形ABCD的边长为8,点E是CD的中点,HG垂直平分AE且分别交AE,BC于点H,G,则BG=_____________.
【答案】1
10.(2023·哈尔滨)如图,在正方形ABCD中,点E在CD上,连接AE,BE,F为BE的中点,连接CF,若CF=,=,则AE的长为__________
【答案】
11.如图,正方形ABCD的边长为8,点M在DC上且DM=2,N是AC上的一动点,则DN+MN的最小值是 .
【答案】10
解析:连接BM交AC于点P,∵点N为AC上的动点,由三角形两边之和大于第三边,且正方形是轴对称图形知,当点N运动到点P时,DN+MN=BP+PM=BM,DN+MN的最小值为BM的长度,∵四边形ABCD为正方形,∴BC=CD=8,CM=8-2=6,∠BCM=90°,∴BM==10,∴DN+MN的最小值是10.
三、解答题
12.如图,已知四边形ABCD是正方形,G为线段AD上任意一点,CE⊥BG于点E,DF⊥CE于点F.求证:DF=BE+EF.
证明:∵四边形ABCD是正方形,∴BC=CD,∠BCD=90°,∵CE⊥BG,DF⊥CE,∴∠BEC=∠DFC=90°,∴∠BCE+∠CBE=90°=∠BCE+∠DCF,∴∠CBE=∠DCF,在△CBE和△DCF中,∴△CBE≌△DCF(AAS),
∴CF=BE,CE=DF,∵CE=CF+EF,∴DF=BE+EF
13.如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=DF,OE=OA.求证:四边形AECF是正方形.
证明:∵四边形ABCD是菱形,∴AC⊥BD,OA=OC,OB=OD,∵BE=DF,∴OE=OF,∴四边形AECF是平行四边形.又∵AC⊥EF,∴四边形AECF是菱形;∵OE=OA=OF,∴OE=OF=OA=OC,即EF=AC,∴菱形AECF是正方形
14.如图所示,顺次延长正方形ABCD的边AB,BC,CD,DA至点E,F,G,H,使BE=CF=DG=AH.求证:四边形EFGH是正方形.
证明:∵四边形ABCD是正方形,∴AB=BC=CD=DA,∠ABC=∠BCD=∠CDA=∠DAB=90°,∴∠EBF=∠HAE=∠GDH=∠FCG,∵BE=CF=DG=AH,∴CG=DH=AE=BF,∴△BFE≌△CGF≌△DHG≌△AEH,∴EF=FG=GH=HE,∠EFB=∠HEA,∴四边形EFGH是菱形,∵∠EFB+∠FEB=90°,∴∠HEA+∠FEB=∠FEH=90°,∴菱形EFGH是正方形
15.如图,点O是线段AB上的一点,OA=OC,OD平分∠AOC交AC于点D,OF平分∠COB,CF⊥OF于点F.
(1)求证:四边形CDOF是矩形;
(2)当∠AOC为多少度时,四边形CDOF是正方形?并说明理由.
解:(1)∵OD平分∠AOC,OF平分∠COB,∴∠AOC=2∠COD,∠COB=2∠COF,∵∠AOC+∠BOC=180°,∴2∠COD+2∠COF=180°,∴∠COD+∠COF=90°,∴∠DOF=90°,∵OA=OC,OD平分∠AOC,∴OD⊥AC,AD=DC,∴∠CDO=90°,∵CF⊥OF,∴∠CFO=90°,∴四边形CDOF是矩形
(2)当∠AOC=90°时,四边形CDOF是正方形;理由如下:∵∠AOC=90°,AD=DC,∴OD=DC;又由(1)知四边形CDOF是矩形,则四边形CDOF是正方形;因此,当∠AOC=90°时,四边形CDOF是正方形
16.将正方形ABCD和菱形EFGH按照如图所示摆放,顶点D与顶点H重合,菱形EFGH的对角线HF经过点B,点E,G分别在AB,BC上.
(1)求证:△ADE≌△CDG;
(2)若AE=BE=2,求BF的长.
解:(1)∵四边形ABCD是正方形,四边形HEFG是菱形,∴AD=CD,ED=GD,∠ADB=∠CDB,∠EHB=∠GHB,∴∠ADB-∠EHB=∠CDB-∠GHB,即∠ADE=∠CDG,∴△ADE≌△CDG(SAS)
(2)过点E作EQ⊥DF于点Q,则∠EQB=90°,∵四边形ABCD是正方形,∴∠A=90°,AD=AB=AE+EB=2+2=4,∠EBQ=∠CBD=45°,∴∠QEB=45°=∠EBQ,∴EQ=BQ,∵BE=2,∴2EQ2=22,∴EQ=BQ=(负数舍去),在Rt△DAE中,由勾股定理得:DE===2,∵四边形EFGH是菱形,∴EF=DE=2,∴QF===3,∴BF=QF-QB=3-=2
18.2.3 正方形
一、选择题
1.正方形具有而菱形不一定具有的性质是( )
A.对角线互相平分 B.对角线相等 C.对角线互相垂直 D.对角线平分一组对角
2.若正方形的一条对角线的长为4,则这个正方形的面积是( )
A.8 B.4 C.8 D.16
3.如图,在正方形ABCD中,对角线AC,BD相交于点O,则图中的等腰直角三角形有( )
A.4个 B.6个 C.8个 D.10个
4.如图,在正方形ABCD的外侧作等边三角形ABE,则∠BED的度数为( )
A.15° B.35° C.45° D.55°
5.下列命题,其中是真命题的是( )
A.对角线互相垂直的四边形是平行四边形 B.有一个角是直角的四边形是矩形
C.对角线互相平分的四边形是菱形 D.对角线互相垂直的矩形是正方形
6.如图,O为正方形ABCD对角线AC的中点,△ACE为等边三角形.若AB=4,则OE的长为( )
A. B.2 C.4 D.4
7.如图,在边长为2的等边三角形ABC的外侧作正方形ABED,过点D作DF⊥BC,垂足为F,则DF的长为( )
A.2+2 B.5- C.3- D.+1
二、填空题
8.(2023·怀化)如图,点P是正方形ABCD的对角线AC上的一点,PE⊥AD于点E,PE=3.则点P到直线AB的距离为________.
9.(2022·无锡)如图,正方形ABCD的边长为8,点E是CD的中点,HG垂直平分AE且分别交AE,BC于点H,G,则BG=_____________.
10.(2023·哈尔滨)如图,在正方形ABCD中,点E在CD上,连接AE,BE,F为BE的中点,连接CF,若CF=,=,则AE的长为__________
11.如图,正方形ABCD的边长为8,点M在DC上且DM=2,N是AC上的一动点,则DN+MN的最小值是 .
三、解答题
12.如图,已知四边形ABCD是正方形,G为线段AD上任意一点,CE⊥BG于点E,DF⊥CE于点F.求证:DF=BE+EF.
13.如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=DF,OE=OA.求证:四边形AECF是正方形.
14.如图所示,顺次延长正方形ABCD的边AB,BC,CD,DA至点E,F,G,H,使BE=CF=DG=AH.求证:四边形EFGH是正方形.
15.如图,点O是线段AB上的一点,OA=OC,OD平分∠AOC交AC于点D,OF平分∠COB,CF⊥OF于点F.
(1)求证:四边形CDOF是矩形;
(2)当∠AOC为多少度时,四边形CDOF是正方形?并说明理由.
16.将正方形ABCD和菱形EFGH按照如图所示摆放,顶点D与顶点H重合,菱形EFGH的对角线HF经过点B,点E,G分别在AB,BC上.
(1)求证:△ADE≌△CDG;
(2)若AE=BE=2,求BF的长.
1
参考答案
一、选择题
1.正方形具有而菱形不一定具有的性质是( B )
A.对角线互相平分 B.对角线相等 C.对角线互相垂直 D.对角线平分一组对角
2.若正方形的一条对角线的长为4,则这个正方形的面积是( A )
A.8 B.4 C.8 D.16
3.如图,在正方形ABCD中,对角线AC,BD相交于点O,则图中的等腰直角三角形有( C )
A.4个 B.6个 C.8个 D.10个
4.如图,在正方形ABCD的外侧作等边三角形ABE,则∠BED的度数为( C )
A.15° B.35° C.45° D.55°
5.下列命题,其中是真命题的是( D )
A.对角线互相垂直的四边形是平行四边形 B.有一个角是直角的四边形是矩形
C.对角线互相平分的四边形是菱形 D.对角线互相垂直的矩形是正方形
6.如图,O为正方形ABCD对角线AC的中点,△ACE为等边三角形.若AB=4,则OE的长为( B )
A. B.2 C.4 D.4
7.如图,在边长为2的等边三角形ABC的外侧作正方形ABED,过点D作DF⊥BC,垂足为F,则DF的长为( D )
A.2+2 B.5- C.3- D.+1
二、填空题
8.(2023·怀化)如图,点P是正方形ABCD的对角线AC上的一点,PE⊥AD于点E,PE=3.则点P到直线AB的距离为________.
【答案】3
9.(2022·无锡)如图,正方形ABCD的边长为8,点E是CD的中点,HG垂直平分AE且分别交AE,BC于点H,G,则BG=_____________.
【答案】1
10.(2023·哈尔滨)如图,在正方形ABCD中,点E在CD上,连接AE,BE,F为BE的中点,连接CF,若CF=,=,则AE的长为__________
【答案】
11.如图,正方形ABCD的边长为8,点M在DC上且DM=2,N是AC上的一动点,则DN+MN的最小值是 .
【答案】10
解析:连接BM交AC于点P,∵点N为AC上的动点,由三角形两边之和大于第三边,且正方形是轴对称图形知,当点N运动到点P时,DN+MN=BP+PM=BM,DN+MN的最小值为BM的长度,∵四边形ABCD为正方形,∴BC=CD=8,CM=8-2=6,∠BCM=90°,∴BM==10,∴DN+MN的最小值是10.
三、解答题
12.如图,已知四边形ABCD是正方形,G为线段AD上任意一点,CE⊥BG于点E,DF⊥CE于点F.求证:DF=BE+EF.
证明:∵四边形ABCD是正方形,∴BC=CD,∠BCD=90°,∵CE⊥BG,DF⊥CE,∴∠BEC=∠DFC=90°,∴∠BCE+∠CBE=90°=∠BCE+∠DCF,∴∠CBE=∠DCF,在△CBE和△DCF中,∴△CBE≌△DCF(AAS),
∴CF=BE,CE=DF,∵CE=CF+EF,∴DF=BE+EF
13.如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=DF,OE=OA.求证:四边形AECF是正方形.
证明:∵四边形ABCD是菱形,∴AC⊥BD,OA=OC,OB=OD,∵BE=DF,∴OE=OF,∴四边形AECF是平行四边形.又∵AC⊥EF,∴四边形AECF是菱形;∵OE=OA=OF,∴OE=OF=OA=OC,即EF=AC,∴菱形AECF是正方形
14.如图所示,顺次延长正方形ABCD的边AB,BC,CD,DA至点E,F,G,H,使BE=CF=DG=AH.求证:四边形EFGH是正方形.
证明:∵四边形ABCD是正方形,∴AB=BC=CD=DA,∠ABC=∠BCD=∠CDA=∠DAB=90°,∴∠EBF=∠HAE=∠GDH=∠FCG,∵BE=CF=DG=AH,∴CG=DH=AE=BF,∴△BFE≌△CGF≌△DHG≌△AEH,∴EF=FG=GH=HE,∠EFB=∠HEA,∴四边形EFGH是菱形,∵∠EFB+∠FEB=90°,∴∠HEA+∠FEB=∠FEH=90°,∴菱形EFGH是正方形
15.如图,点O是线段AB上的一点,OA=OC,OD平分∠AOC交AC于点D,OF平分∠COB,CF⊥OF于点F.
(1)求证:四边形CDOF是矩形;
(2)当∠AOC为多少度时,四边形CDOF是正方形?并说明理由.
解:(1)∵OD平分∠AOC,OF平分∠COB,∴∠AOC=2∠COD,∠COB=2∠COF,∵∠AOC+∠BOC=180°,∴2∠COD+2∠COF=180°,∴∠COD+∠COF=90°,∴∠DOF=90°,∵OA=OC,OD平分∠AOC,∴OD⊥AC,AD=DC,∴∠CDO=90°,∵CF⊥OF,∴∠CFO=90°,∴四边形CDOF是矩形
(2)当∠AOC=90°时,四边形CDOF是正方形;理由如下:∵∠AOC=90°,AD=DC,∴OD=DC;又由(1)知四边形CDOF是矩形,则四边形CDOF是正方形;因此,当∠AOC=90°时,四边形CDOF是正方形
16.将正方形ABCD和菱形EFGH按照如图所示摆放,顶点D与顶点H重合,菱形EFGH的对角线HF经过点B,点E,G分别在AB,BC上.
(1)求证:△ADE≌△CDG;
(2)若AE=BE=2,求BF的长.
解:(1)∵四边形ABCD是正方形,四边形HEFG是菱形,∴AD=CD,ED=GD,∠ADB=∠CDB,∠EHB=∠GHB,∴∠ADB-∠EHB=∠CDB-∠GHB,即∠ADE=∠CDG,∴△ADE≌△CDG(SAS)
(2)过点E作EQ⊥DF于点Q,则∠EQB=90°,∵四边形ABCD是正方形,∴∠A=90°,AD=AB=AE+EB=2+2=4,∠EBQ=∠CBD=45°,∴∠QEB=45°=∠EBQ,∴EQ=BQ,∵BE=2,∴2EQ2=22,∴EQ=BQ=(负数舍去),在Rt△DAE中,由勾股定理得:DE===2,∵四边形EFGH是菱形,∴EF=DE=2,∴QF===3,∴BF=QF-QB=3-=2
