初中数学人教版八年级下册18.2.2.2 菱形的判定 同步训练 含答案
文档属性
| 名称 | 初中数学人教版八年级下册18.2.2.2 菱形的判定 同步训练 含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 199.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-04 22:00:12 | ||
图片预览

文档简介
第十八章 平行四边形
18.2.2 菱形
第2课时 菱形的判定
一、选择题
1.如图,要使 ABCD成为菱形,则需添加的一个条件是( )
A.AC=AD B.BA=BC C.∠ABC=90° D.AC=BD
2.能判定一个四边形是菱形的是( )
A.对角线相等的四边形是菱形 B.对角线互相垂直的四边形是菱形
C.对角线互相垂直平分的四边形是菱形 D.对角线相等且互相平分的四边形是菱形
3.下列命题中,正确的是( )
A.有一个角是60°的平行四边形是菱形 B.有一组邻边相等的四边形是菱形
C.有两边相等的平行四边形是菱形 D.四条边相等的四边形是菱形
4.若四边形的两条对角线分别平分两组对角,则该四边形一定是( )
A.平行四边形 B.矩形 C.菱形 D.以上都有可能
5.如图,四边形ABCD的两条对角线相交于点O,且互相平分.添加下列条件,仍不能判定四边形ABCD为菱形的是( )
A.AC⊥BD B.AB=AD C.AC=BD D.∠ABD=∠CBD
6.如图,在△ABC中,D是BC边的中点,点E,F分别在线段AD及其延长线上,DE=DF.在下列条件中,使四边形BECF是菱形的是( )
A.EB⊥EC B.AB⊥AC C.AB=AC D.BF∥CE
二、填空题
7.(2022·营口)如图,将△ABC沿着BC方向平移得到△DEF,只需添加一个条件即可证明四边形ABED是菱形,这个条件可以是____________________________.(写出一个即可)
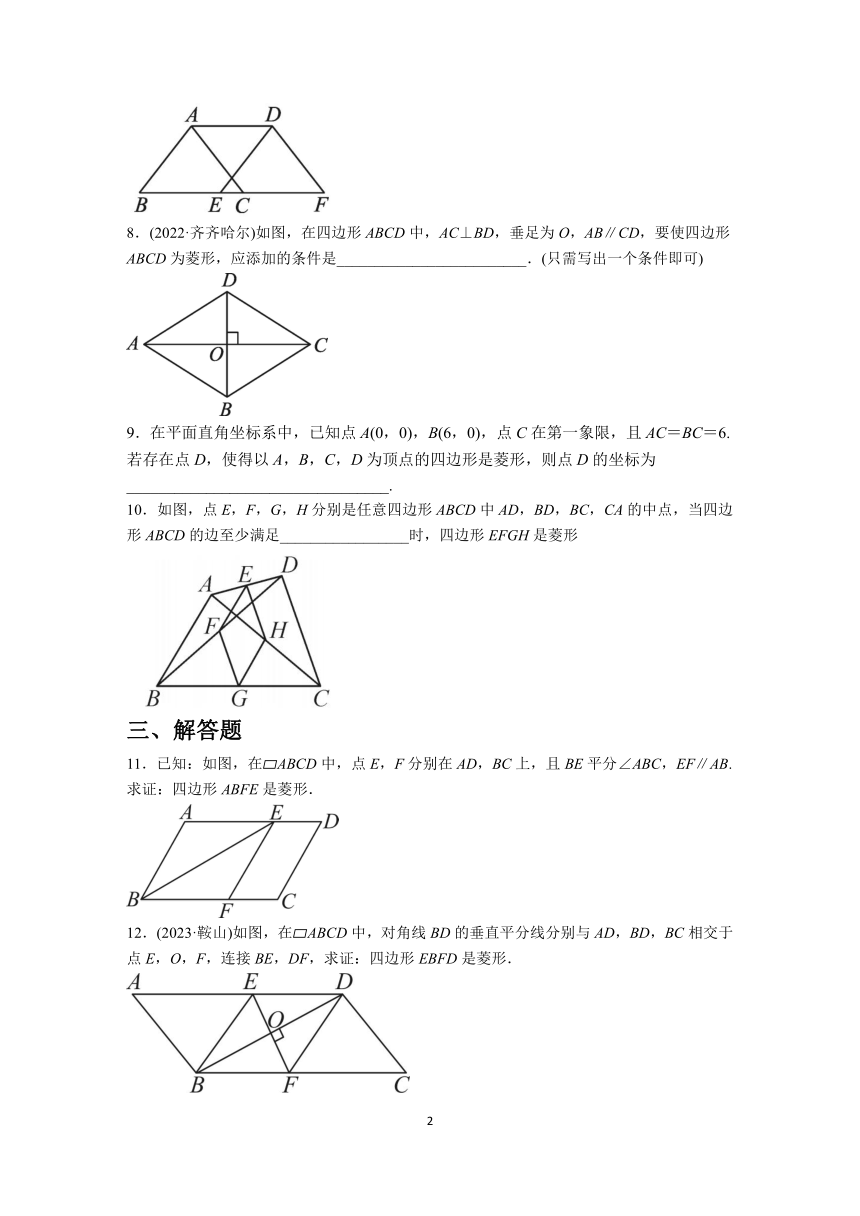
8.(2022·齐齐哈尔)如图,在四边形ABCD中,AC⊥BD,垂足为O,AB∥CD,要使四边形ABCD为菱形,应添加的条件是_________________________.(只需写出一个条件即可)
9.在平面直角坐标系中,已知点A(0,0),B(6,0),点C在第一象限,且AC=BC=6.若存在点D,使得以A,B,C,D为顶点的四边形是菱形,则点D的坐标为_________________________________.
10.如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,BC,CA的中点,当四边形ABCD的边至少满足_________________时,四边形EFGH是菱形
三、解答题
11.已知:如图,在 ABCD中,点E,F分别在AD,BC上,且BE平分∠ABC,EF∥AB.求证:四边形ABFE是菱形.
12.(2023·鞍山)如图,在 ABCD中,对角线BD的垂直平分线分别与AD,BD,BC相交于点E,O,F,连接BE,DF,求证:四边形EBFD是菱形.
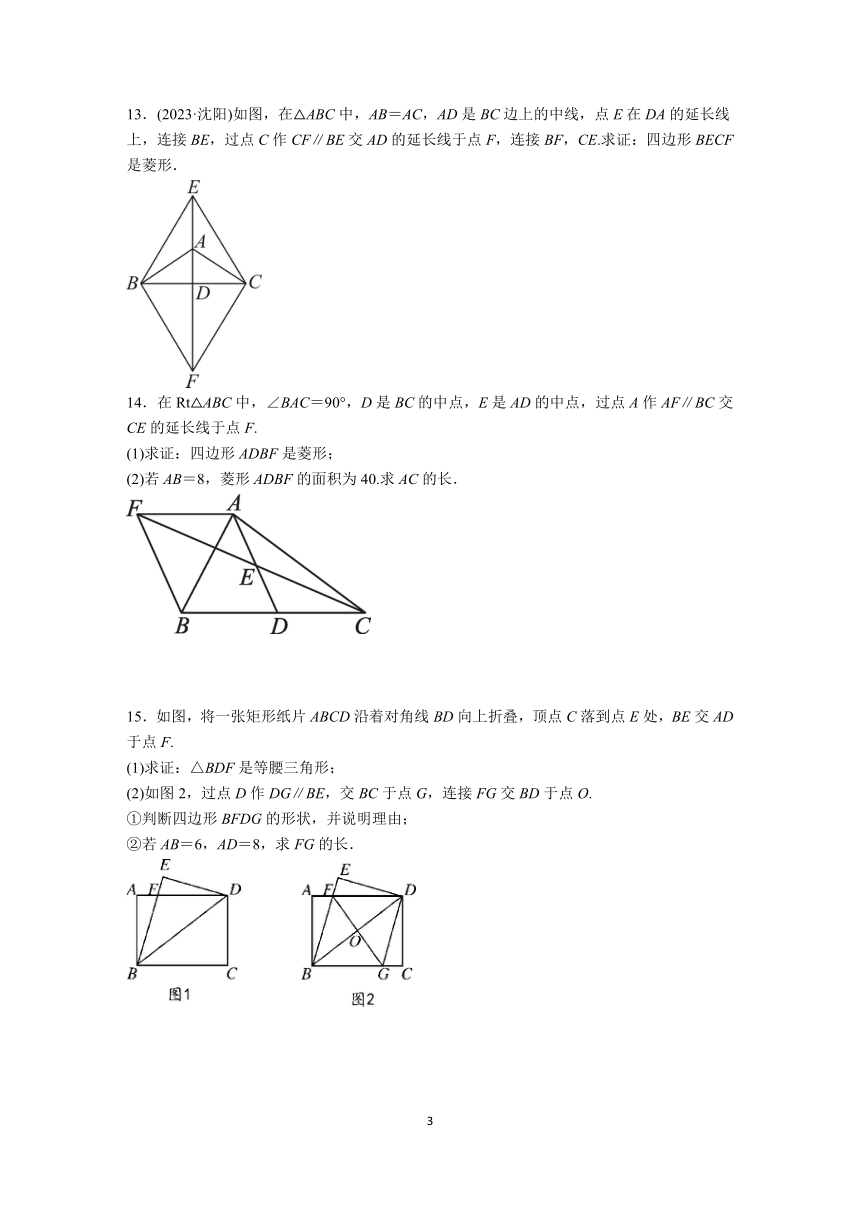
13.(2023·沈阳)如图,在△ABC中,AB=AC,AD是BC边上的中线,点E在DA的延长线上,连接BE,过点C作CF∥BE交AD的延长线于点F,连接BF,CE.求证:四边形BECF是菱形.
14.在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交CE的延长线于点F.
(1)求证:四边形ADBF是菱形;
(2)若AB=8,菱形ADBF的面积为40.求AC的长.
15.如图,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
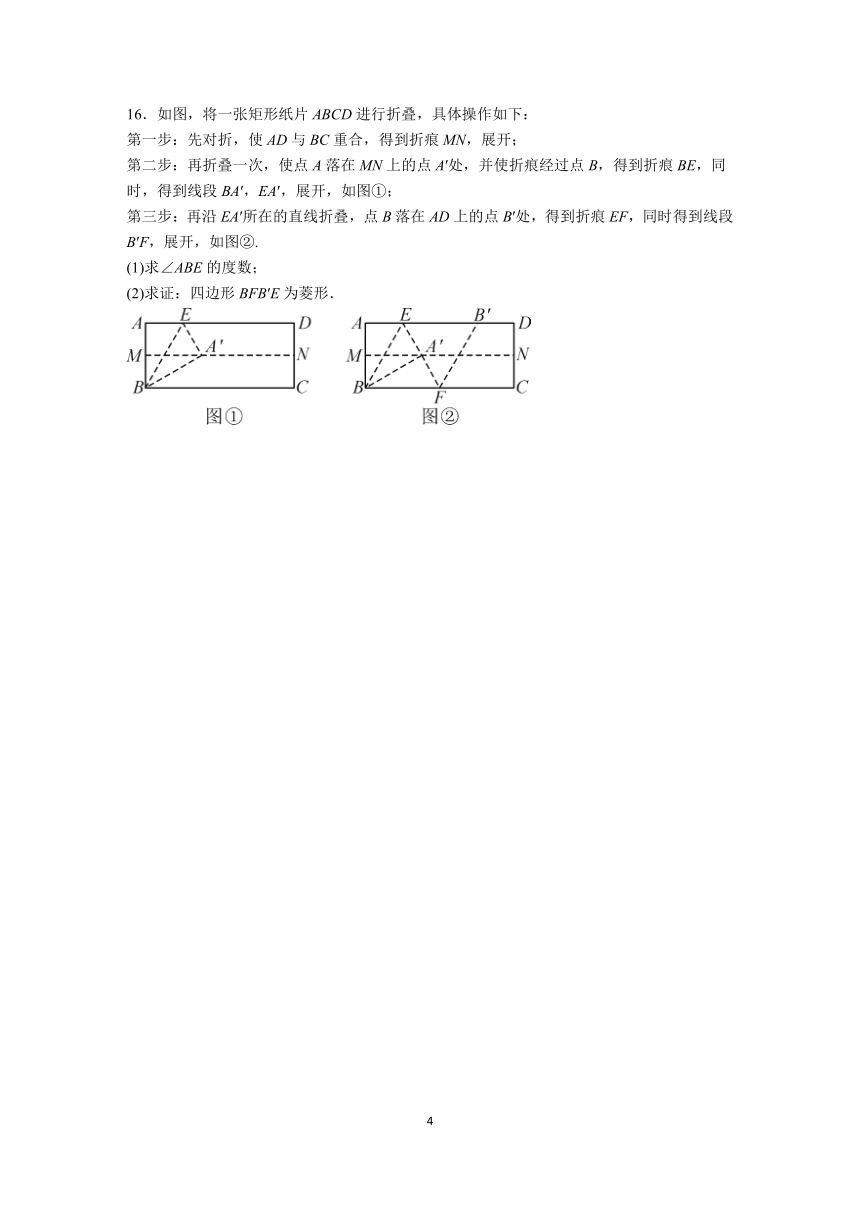
16.如图,将一张矩形纸片ABCD进行折叠,具体操作如下:
第一步:先对折,使AD与BC重合,得到折痕MN,展开;
第二步:再折叠一次,使点A落在MN上的点A′处,并使折痕经过点B,得到折痕BE,同时,得到线段BA′,EA′,展开,如图①;
第三步:再沿EA′所在的直线折叠,点B落在AD上的点B′处,得到折痕EF,同时得到线段B′F,展开,如图②.
(1)求∠ABE的度数;
(2)求证:四边形BFB′E为菱形.
1
参考答案
一、选择题
1.如图,要使 ABCD成为菱形,则需添加的一个条件是( B )
A.AC=AD B.BA=BC C.∠ABC=90° D.AC=BD
2.能判定一个四边形是菱形的是( C )
A.对角线相等的四边形是菱形 B.对角线互相垂直的四边形是菱形
C.对角线互相垂直平分的四边形是菱形 D.对角线相等且互相平分的四边形是菱形
3.下列命题中,正确的是( D )
A.有一个角是60°的平行四边形是菱形 B.有一组邻边相等的四边形是菱形
C.有两边相等的平行四边形是菱形 D.四条边相等的四边形是菱形
4.若四边形的两条对角线分别平分两组对角,则该四边形一定是( C )
A.平行四边形 B.矩形 C.菱形 D.以上都有可能
5.如图,四边形ABCD的两条对角线相交于点O,且互相平分.添加下列条件,仍不能判定四边形ABCD为菱形的是( C )
A.AC⊥BD B.AB=AD C.AC=BD D.∠ABD=∠CBD
6.如图,在△ABC中,D是BC边的中点,点E,F分别在线段AD及其延长线上,DE=DF.在下列条件中,使四边形BECF是菱形的是( C )
A.EB⊥EC B.AB⊥AC C.AB=AC D.BF∥CE
二、填空题
7.(2022·营口)如图,将△ABC沿着BC方向平移得到△DEF,只需添加一个条件即可证明四边形ABED是菱形,这个条件可以是____________________________.(写出一个即可)
【答案】AB=AD(答案不唯一)
8.(2022·齐齐哈尔)如图,在四边形ABCD中,AC⊥BD,垂足为O,AB∥CD,要使四边形ABCD为菱形,应添加的条件是_________________________.(只需写出一个条件即可)
【答案】AB=CD(答案不唯一)
9.在平面直角坐标系中,已知点A(0,0),B(6,0),点C在第一象限,且AC=BC=6.若存在点D,使得以A,B,C,D为顶点的四边形是菱形,则点D的坐标为_________________________________.
【答案】(9,3)
10.如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,BC,CA的中点,当四边形ABCD的边至少满足_________________时,四边形EFGH是菱形
【答案】AB=CD
三、解答题
11.已知:如图,在 ABCD中,点E,F分别在AD,BC上,且BE平分∠ABC,EF∥AB.求证:四边形ABFE是菱形.
证明:∵四边形ABCD是平行四边形,∴AD∥BC,又∵EF∥AB,∴四边形ABFE是平行四边形,∵BE平分∠ABC,∴∠ABE=∠FBE,∵AD∥BC,∴∠AEB=∠FBE,∴∠ABE=∠AEB,∴AB=AE,∴平行四边形ABFE是菱形
12.(2023·鞍山)如图,在 ABCD中,对角线BD的垂直平分线分别与AD,BD,BC相交于点E,O,F,连接BE,DF,求证:四边形EBFD是菱形.
证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠EDO=∠OBF,∵O是BD中点,∴BO=DO,在△DEO和△BFO中, ∴△DEO≌△BFO (ASA),∴OE=OF,∴四边形EBFD是平行四边形,又∵EF⊥BD,∴四边形EBFD是菱形
13.(2023·沈阳)如图,在△ABC中,AB=AC,AD是BC边上的中线,点E在DA的延长线上,连接BE,过点C作CF∥BE交AD的延长线于点F,连接BF,CE.求证:四边形BECF是菱形.
证明:∵AB=AC,AD是BC边上的中线,∴AD垂直平分BC,∴EB=EC,FB=FC,∵CF∥BE,∴∠BED=∠CFD,∠EBD=∠FCD,∵DB=CD,∴△EBD≌△FCD(AAS),∴BE=FC,∴EB=BF=FC=EC,∴四边形EBFC是菱形
14.在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交CE的延长线于点F.
(1)求证:四边形ADBF是菱形;
(2)若AB=8,菱形ADBF的面积为40.求AC的长.
解:(1)∵AF∥BC,∴∠AFC=∠FCD,∠FAE=∠CDE,∵点E是AD的中点,∴AE=DE,∴△FAE≌△CDE(AAS),∴AF=CD,∵点D是BC的中点,∴BD=CD,∴AF=BD,∴四边形ADBF是平行四边形,∵∠BAC=90°,D是BC的中点,∴AD=BD=BC,∴四边形ADBF是菱形
(2)∵四边形ADBF是菱形,∴S菱形ADBF=2S△ABD,∵点D是BC的中点,∴S△ABC=2S△ABD,∴S菱形ADBF=S△ABC=40,∴AB·AC=40,∵AB=8,∴AC=10
15.如图,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
(1)证明:根据折叠,∠DBC=∠DBE, 又AD∥BC,∴∠DBC=∠ADB,∴∠DBE=∠ADB,∴DF=BF,∴△BDF是等腰三角形;
(2)解:①∵四边形ABCD是矩形,∴AD∥BC,∴FD∥BG,又∵FB∥DG,∴四边形BFDG是平行四边形,∵DF=BF,∴四边形BFDG是菱形; ②∵AB=6,AD=8,∴BD=10,∴OB=BD=5.假设DF=BF=x,∴AF=AD-DF=8-x.∴在直角△ABF中,AB2+AF2=BF2,即62+(8-x)2=x2,解得x=,即BF=,∴FO===,∴FG=2FO=.
16.如图,将一张矩形纸片ABCD进行折叠,具体操作如下:
第一步:先对折,使AD与BC重合,得到折痕MN,展开;
第二步:再折叠一次,使点A落在MN上的点A′处,并使折痕经过点B,得到折痕BE,同时,得到线段BA′,EA′,展开,如图①;
第三步:再沿EA′所在的直线折叠,点B落在AD上的点B′处,得到折痕EF,同时得到线段B′F,展开,如图②.
(1)求∠ABE的度数;
(2)求证:四边形BFB′E为菱形.
解:(1)∵第二步折叠使点A落在MN上的点A′处,并使折痕经过点B,得到折痕BE,∴∠AEB=∠A′EB.∵第三步折叠,点B落在AD上的点B′处,得到折痕EF,同时得到线段B′F,∴∠A′EB=∠FEB′.∵∠AEB+∠A′EB+∠FEB′=180°,∴∠AEB=∠A′EB=∠FEB′=60°,∴∠ABE=30°
(2)∵沿EA′所在的直线折叠,点B落在AD上的点B′处,∴BE=B′E,BF=B′F.∵AD∥BC,∴∠BFE=∠FEB′=60°,又∠FEB=60°,∴∠FEB=∠BFE,∴BE=BF,∴BE=B′E=B′F=BF,∴四边形BFB′E为菱形
18.2.2 菱形
第2课时 菱形的判定
一、选择题
1.如图,要使 ABCD成为菱形,则需添加的一个条件是( )
A.AC=AD B.BA=BC C.∠ABC=90° D.AC=BD
2.能判定一个四边形是菱形的是( )
A.对角线相等的四边形是菱形 B.对角线互相垂直的四边形是菱形
C.对角线互相垂直平分的四边形是菱形 D.对角线相等且互相平分的四边形是菱形
3.下列命题中,正确的是( )
A.有一个角是60°的平行四边形是菱形 B.有一组邻边相等的四边形是菱形
C.有两边相等的平行四边形是菱形 D.四条边相等的四边形是菱形
4.若四边形的两条对角线分别平分两组对角,则该四边形一定是( )
A.平行四边形 B.矩形 C.菱形 D.以上都有可能
5.如图,四边形ABCD的两条对角线相交于点O,且互相平分.添加下列条件,仍不能判定四边形ABCD为菱形的是( )
A.AC⊥BD B.AB=AD C.AC=BD D.∠ABD=∠CBD
6.如图,在△ABC中,D是BC边的中点,点E,F分别在线段AD及其延长线上,DE=DF.在下列条件中,使四边形BECF是菱形的是( )
A.EB⊥EC B.AB⊥AC C.AB=AC D.BF∥CE
二、填空题
7.(2022·营口)如图,将△ABC沿着BC方向平移得到△DEF,只需添加一个条件即可证明四边形ABED是菱形,这个条件可以是____________________________.(写出一个即可)
8.(2022·齐齐哈尔)如图,在四边形ABCD中,AC⊥BD,垂足为O,AB∥CD,要使四边形ABCD为菱形,应添加的条件是_________________________.(只需写出一个条件即可)
9.在平面直角坐标系中,已知点A(0,0),B(6,0),点C在第一象限,且AC=BC=6.若存在点D,使得以A,B,C,D为顶点的四边形是菱形,则点D的坐标为_________________________________.
10.如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,BC,CA的中点,当四边形ABCD的边至少满足_________________时,四边形EFGH是菱形
三、解答题
11.已知:如图,在 ABCD中,点E,F分别在AD,BC上,且BE平分∠ABC,EF∥AB.求证:四边形ABFE是菱形.
12.(2023·鞍山)如图,在 ABCD中,对角线BD的垂直平分线分别与AD,BD,BC相交于点E,O,F,连接BE,DF,求证:四边形EBFD是菱形.
13.(2023·沈阳)如图,在△ABC中,AB=AC,AD是BC边上的中线,点E在DA的延长线上,连接BE,过点C作CF∥BE交AD的延长线于点F,连接BF,CE.求证:四边形BECF是菱形.
14.在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交CE的延长线于点F.
(1)求证:四边形ADBF是菱形;
(2)若AB=8,菱形ADBF的面积为40.求AC的长.
15.如图,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
16.如图,将一张矩形纸片ABCD进行折叠,具体操作如下:
第一步:先对折,使AD与BC重合,得到折痕MN,展开;
第二步:再折叠一次,使点A落在MN上的点A′处,并使折痕经过点B,得到折痕BE,同时,得到线段BA′,EA′,展开,如图①;
第三步:再沿EA′所在的直线折叠,点B落在AD上的点B′处,得到折痕EF,同时得到线段B′F,展开,如图②.
(1)求∠ABE的度数;
(2)求证:四边形BFB′E为菱形.
1
参考答案
一、选择题
1.如图,要使 ABCD成为菱形,则需添加的一个条件是( B )
A.AC=AD B.BA=BC C.∠ABC=90° D.AC=BD
2.能判定一个四边形是菱形的是( C )
A.对角线相等的四边形是菱形 B.对角线互相垂直的四边形是菱形
C.对角线互相垂直平分的四边形是菱形 D.对角线相等且互相平分的四边形是菱形
3.下列命题中,正确的是( D )
A.有一个角是60°的平行四边形是菱形 B.有一组邻边相等的四边形是菱形
C.有两边相等的平行四边形是菱形 D.四条边相等的四边形是菱形
4.若四边形的两条对角线分别平分两组对角,则该四边形一定是( C )
A.平行四边形 B.矩形 C.菱形 D.以上都有可能
5.如图,四边形ABCD的两条对角线相交于点O,且互相平分.添加下列条件,仍不能判定四边形ABCD为菱形的是( C )
A.AC⊥BD B.AB=AD C.AC=BD D.∠ABD=∠CBD
6.如图,在△ABC中,D是BC边的中点,点E,F分别在线段AD及其延长线上,DE=DF.在下列条件中,使四边形BECF是菱形的是( C )
A.EB⊥EC B.AB⊥AC C.AB=AC D.BF∥CE
二、填空题
7.(2022·营口)如图,将△ABC沿着BC方向平移得到△DEF,只需添加一个条件即可证明四边形ABED是菱形,这个条件可以是____________________________.(写出一个即可)
【答案】AB=AD(答案不唯一)
8.(2022·齐齐哈尔)如图,在四边形ABCD中,AC⊥BD,垂足为O,AB∥CD,要使四边形ABCD为菱形,应添加的条件是_________________________.(只需写出一个条件即可)
【答案】AB=CD(答案不唯一)
9.在平面直角坐标系中,已知点A(0,0),B(6,0),点C在第一象限,且AC=BC=6.若存在点D,使得以A,B,C,D为顶点的四边形是菱形,则点D的坐标为_________________________________.
【答案】(9,3)
10.如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,BC,CA的中点,当四边形ABCD的边至少满足_________________时,四边形EFGH是菱形
【答案】AB=CD
三、解答题
11.已知:如图,在 ABCD中,点E,F分别在AD,BC上,且BE平分∠ABC,EF∥AB.求证:四边形ABFE是菱形.
证明:∵四边形ABCD是平行四边形,∴AD∥BC,又∵EF∥AB,∴四边形ABFE是平行四边形,∵BE平分∠ABC,∴∠ABE=∠FBE,∵AD∥BC,∴∠AEB=∠FBE,∴∠ABE=∠AEB,∴AB=AE,∴平行四边形ABFE是菱形
12.(2023·鞍山)如图,在 ABCD中,对角线BD的垂直平分线分别与AD,BD,BC相交于点E,O,F,连接BE,DF,求证:四边形EBFD是菱形.
证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠EDO=∠OBF,∵O是BD中点,∴BO=DO,在△DEO和△BFO中, ∴△DEO≌△BFO (ASA),∴OE=OF,∴四边形EBFD是平行四边形,又∵EF⊥BD,∴四边形EBFD是菱形
13.(2023·沈阳)如图,在△ABC中,AB=AC,AD是BC边上的中线,点E在DA的延长线上,连接BE,过点C作CF∥BE交AD的延长线于点F,连接BF,CE.求证:四边形BECF是菱形.
证明:∵AB=AC,AD是BC边上的中线,∴AD垂直平分BC,∴EB=EC,FB=FC,∵CF∥BE,∴∠BED=∠CFD,∠EBD=∠FCD,∵DB=CD,∴△EBD≌△FCD(AAS),∴BE=FC,∴EB=BF=FC=EC,∴四边形EBFC是菱形
14.在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交CE的延长线于点F.
(1)求证:四边形ADBF是菱形;
(2)若AB=8,菱形ADBF的面积为40.求AC的长.
解:(1)∵AF∥BC,∴∠AFC=∠FCD,∠FAE=∠CDE,∵点E是AD的中点,∴AE=DE,∴△FAE≌△CDE(AAS),∴AF=CD,∵点D是BC的中点,∴BD=CD,∴AF=BD,∴四边形ADBF是平行四边形,∵∠BAC=90°,D是BC的中点,∴AD=BD=BC,∴四边形ADBF是菱形
(2)∵四边形ADBF是菱形,∴S菱形ADBF=2S△ABD,∵点D是BC的中点,∴S△ABC=2S△ABD,∴S菱形ADBF=S△ABC=40,∴AB·AC=40,∵AB=8,∴AC=10
15.如图,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
(1)证明:根据折叠,∠DBC=∠DBE, 又AD∥BC,∴∠DBC=∠ADB,∴∠DBE=∠ADB,∴DF=BF,∴△BDF是等腰三角形;
(2)解:①∵四边形ABCD是矩形,∴AD∥BC,∴FD∥BG,又∵FB∥DG,∴四边形BFDG是平行四边形,∵DF=BF,∴四边形BFDG是菱形; ②∵AB=6,AD=8,∴BD=10,∴OB=BD=5.假设DF=BF=x,∴AF=AD-DF=8-x.∴在直角△ABF中,AB2+AF2=BF2,即62+(8-x)2=x2,解得x=,即BF=,∴FO===,∴FG=2FO=.
16.如图,将一张矩形纸片ABCD进行折叠,具体操作如下:
第一步:先对折,使AD与BC重合,得到折痕MN,展开;
第二步:再折叠一次,使点A落在MN上的点A′处,并使折痕经过点B,得到折痕BE,同时,得到线段BA′,EA′,展开,如图①;
第三步:再沿EA′所在的直线折叠,点B落在AD上的点B′处,得到折痕EF,同时得到线段B′F,展开,如图②.
(1)求∠ABE的度数;
(2)求证:四边形BFB′E为菱形.
解:(1)∵第二步折叠使点A落在MN上的点A′处,并使折痕经过点B,得到折痕BE,∴∠AEB=∠A′EB.∵第三步折叠,点B落在AD上的点B′处,得到折痕EF,同时得到线段B′F,∴∠A′EB=∠FEB′.∵∠AEB+∠A′EB+∠FEB′=180°,∴∠AEB=∠A′EB=∠FEB′=60°,∴∠ABE=30°
(2)∵沿EA′所在的直线折叠,点B落在AD上的点B′处,∴BE=B′E,BF=B′F.∵AD∥BC,∴∠BFE=∠FEB′=60°,又∠FEB=60°,∴∠FEB=∠BFE,∴BE=BF,∴BE=B′E=B′F=BF,∴四边形BFB′E为菱形
