3.1长方体和正方体的认识同步分层作业-2023-2024学年五年级数学下册同步分层作业设计(人教版)(含解析)
文档属性
| 名称 | 3.1长方体和正方体的认识同步分层作业-2023-2024学年五年级数学下册同步分层作业设计(人教版)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 135.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-04 23:19:46 | ||
图片预览




文档简介
3.1 长方体和正方体的认识同步分层作业
知识点:
1、长方体各部分的名称:围成长方体的长方形(或正方形)叫做长方体的面,面和面相交的线 段叫做棱,棱和棱的交点叫做顶点。
2、
3、相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高,如图:
长方体有 4 条长,4 条宽和4条高。
4、正方体的 6 个面是完全相同的正方形,12 条棱的长度都相等,有 8 个顶点。正方体是特殊的长方体。
一、填空题
1.魔方是常见的( )体,它有( )个面,( )条棱,8个( )。
2.一个长方体有( )个顶点,有( )个面,这些面都是( )形或( )形。一个长方体中,至少有( )个面是完全相同的。
3.如图,长方体一共有( )条棱,棱长是5cm的棱有( )条,棱长是4cm的棱有( )条,棱长是3cm的棱有( )条,所有棱长的和是( )cm。
4.一个正方体纸盒每个面的周长都是20厘米,它的棱长是( )厘米,棱长总和是( )厘米。
5.用一根长3.6m的铁丝,做成一个长0.4m,宽0.3m的长方体框架,这个框架的高是( )。
6.用铁丝做一个棱长是2dm的正方体框架,至少需要铁丝( )dm。
7.正方体是由6个完全相同的( )围成的立体图形,所有的棱长都( )。
8.用铁丝焊接一个长方体框架,同一顶点上的三根铁丝长分别为18cm,15cm和9cm,一共用( )cm铁丝。
9.在图的长方体中,相交于同一顶点的三条棱长之和是12分米,一只蚂蚁从点A沿着长方体框架的棱爬到点B,至少要爬( )分米。
二、选择题
10.下面选项中,不是正方体展开图的是( )。
A. B. C. D.
11.有一根铁丝,恰好可以围成长6厘米、宽3厘米、高3厘米的长方体框架,这根铁丝恰好也可以围成一个正方体框架,则围成的正方体框架的棱长是( )厘米。
A.1 B.4 C.8 D.16
12.用丝带扎一个礼品盒(如下图所示),接头处长15厘米,捆扎一个礼品盒至少需要( )分米丝带。
A.20 B.21.5 C.22.5 D.23.5
13.若一个正方体棱和扩大到原来的2倍,则这个正方体的棱长总和扩大到原来的( )倍。
A.2 B.8 C.12 D.24
14.小明有10根5厘米长的小棒和6根3厘米长的小棒,他用其中的12根搭成了一个长方体框架,长方体框架的棱长总和是( )厘米。
A.48 B.52 C.56 D.68
15.中国古代的士人学习的“六艺”是“礼、乐、射、御、书、数”。在正方体的6个面上分别写着“六艺”中的一种。正方体展开后如图,与“御”相对的是( )。
A.数 B.乐 C.礼
16.如图是一个长方体物品的长、宽、高,请你根据具体数据估计这可能是( )。
A.书包 B.文具盒 C.数学书 D.粉笔盒
三、判断题
17.一个长方体至少有4个长方形的面。( )
18.底面是正方形的长方体,一定有4个面的面积相等。( )
19.长方体相邻的两个面可能完全相同。( )
20.如果一个长方体有一组相对的面是正方形,则其余四个面完全相同。( )
21.长方体的各个面中可能有正方形,正方体的各个面中可能有长方形。( )
四、解答题
22.如下图,正方体的6个面上分别写着1、2、3、4、5、6。与1相对的面上写着什么数字?与3相对的面上写着什么数字?与4相对的面上写着什么数字?
23.一个长方体的棱长总和是48厘米,长6厘米,宽4厘米,高是多少厘米?
24.科技小组用60厘米的铁丝做一个长方体模型,这个长方体的长是6厘米,宽是5厘米,高是多少厘米?
25.一个长方体纸盒的长、宽、高分别是15cm、8cm、10cm,把它平放在桌面上,它占桌面的最大面积是多少?最小呢?
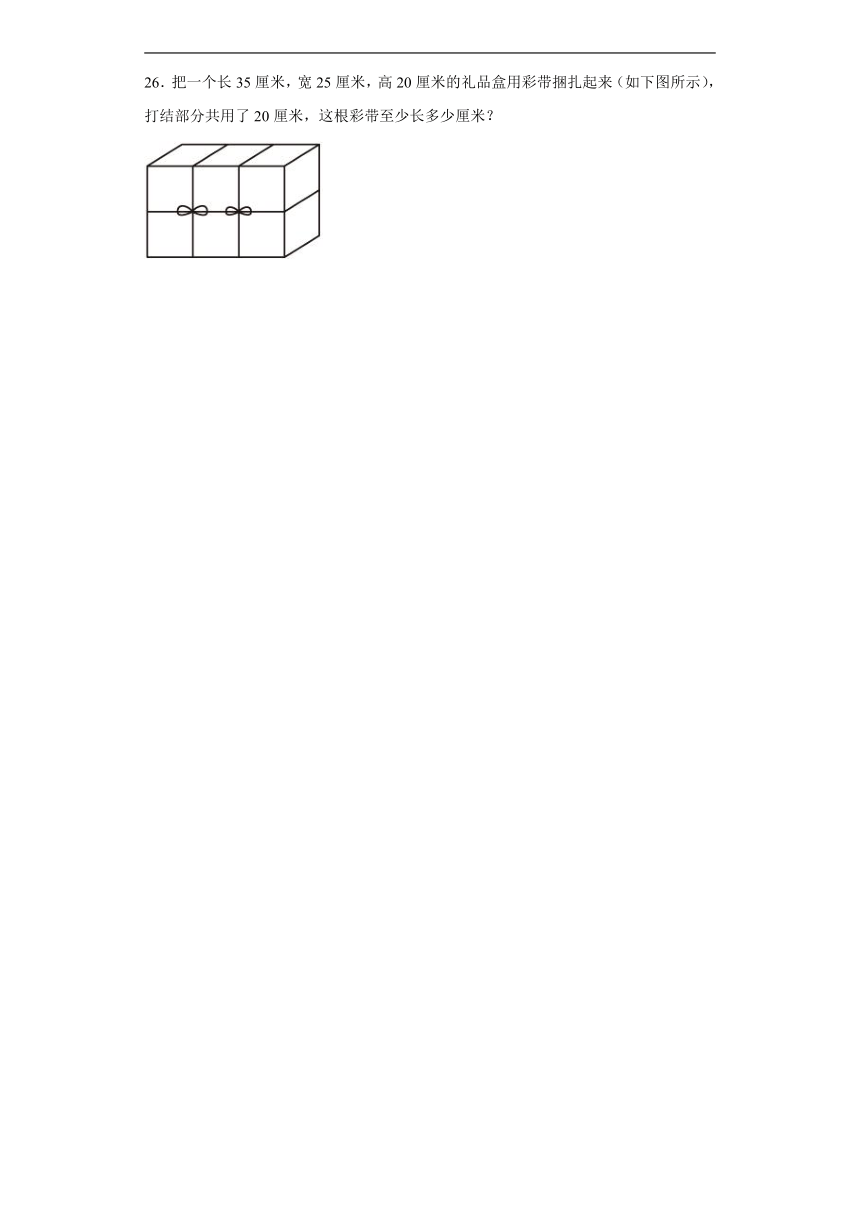
26.把一个长35厘米,宽25厘米,高20厘米的礼品盒用彩带捆扎起来(如下图所示),打结部分共用了20厘米,这根彩带至少长多少厘米?
参考答案:
1. 正方 6 12 顶点
【分析】由6个完全相同的正方形围成的立体图形叫做正方体,也叫立方体,是特殊的长方体。根据正方体的特征:有6个面,这6个面都是正方形,且面积相等;有12条棱,这些棱的长度都相等;有8个顶点,据此解答。
【详解】魔方是常见的(正方)体,它有(6)个面,(12)条棱,8个(顶点)。
2. 8 6 长方 正方 2
【分析】根据长方体的特征:长方体有8个顶点,有6个面,每个面的形状都是长方形或正方形,在长方形中两个相对的面完全相同,一共有3组这样的面。据此可得出答案。
【详解】一个长方体有8个顶点,有6个面,这些面都是长方形或正方形。一个长方体中,至少有2个面是完全相同的。
3. 12 4 4 4 48
【分析】
长方体有12条棱,相对的四条棱长度相等;按长度可分为三组,每一组有4条棱;根据长方体棱长总和=(长+宽+高)×4,列式计算即可求出棱长总和。
【详解】3×4+4×4+5×4
=12+16+20
=28+20
=48(cm)
长方体一共有12条棱,棱长是5cm的棱有4条,棱长是4cm的棱有4条,棱长是3cm的棱有4条,所有棱长的和是48cm。
4. 5 60
【分析】正方体每个面都是完全一样的正方形,根据正方形边长=周长÷4,即可求出正方体棱长,根据正方体棱长总和=棱长×12,求出棱长总和即可。
【详解】20÷4=5(厘米)
5×12=60(厘米)
它的棱长是5厘米,棱长总和是60厘米。
【点睛】关键是熟悉正方体特征,掌握并灵活运用正方体棱长总和公式。
5.0.2m
【分析】根据题意,可知“(长+宽+高)×4=铁丝的总长度” ,据此用铁丝的总长度除以4可以求出一组长、宽、高的和,再减去长和宽即可求出高。
【详解】3.6÷4-0.4-0.3
=0.9-0.4-0.3
=0.2(m)
【点睛】明确长方体棱长总和与长、宽、高的关系是解答本题的关键。
6.24
【分析】由题意可知,要求的是正方体的总棱长,根据正方体的总棱长=棱长×12,据此可解答。
【详解】2×12=24(分米)
【点睛】本题考查正方体的总棱长,熟记正方体的总棱长公式是关键。
7. 正方形 相等
【分析】正方体的特征:6个面都相等,有12条棱,每条棱都相等;据此解答。
【详解】正方体是由6个完全相同的正方形围成的立体图形,所有的棱长都相等。
故答案为:正方形;相等
【点睛】本题考查了正方体的特点;关键是要掌握正方体的特征并灵活运用。
8.168
【分析】求用了多少铁丝就是求出这个长方体框架的棱长总和,从同一个顶点连接的三条棱是一组长宽高,根据长方体的棱长总和=4×(长+宽+高),代入数据即可求解。
【详解】(18+15+9)×4
=42×4
=168(cm)
【点睛】此题考查长方体的棱长总和公式,意识到同一个顶点连接的三条棱是一组长宽高也是解题的关键。
9.12
【分析】
根据题意可知:蚂蚁从A点沿着一个长方体框架的棱爬到B点,至少应爬一个高、一个长、一个宽,12就是长方体的长宽高的和,据此即可解答。
【详解】在如图的长方体中,相交于同一顶点的三条棱长之和是12分米,一只蚂蚁从点A沿着长方体框架的棱爬到点B,至少要爬12分米。
10.D
【分析】正方体的十一种展开图可记忆口诀:一三二,一四一,一在同层可任意,两个三,日状连,三个二,成阶梯,相邻必有日,整体没有田。据此解答。
【详解】A.根据口诀可知,一行有4个的,只能是一四一,所以A符合;
B.根据口诀可知,一行有3个的,可以是一三二,且没有“田”字状,所以B符合;
C.根据口诀可知,三个二成阶梯, 且没有“田”字状,所以C符合;
D.根据口诀可知,一行有4个的,只能是一四一,且一和一不能相连,所以D不符合。
故答案为:D
【点睛】本题主要考查的是正方体的展开图,培养学生的空间想象能力。
11.B
【分析】根据长方体的总棱长公式:L=(a+b+h)×4,据此求出铁丝的长度,铁丝的长度也是正方体框架的总棱长,再根据正方体的总棱长公式:L=12a,用铁丝的长度除以12即可求出正方体框架的棱长。
【详解】(6+3+3)×4
=12×4
=48(厘米)
48÷12=4(厘米)
则围成的正方体框架的棱长是4厘米。
故答案为:B
12.B
【分析】通过观察图形可知,捆扎这个礼品盒需要丝带的长度等于这个长方体的两条长加两条宽加4条高再加上接头处用的15厘米,据此列式解答。
【详解】30×2+20×2+25×4+15
=60+40+100+15
=100+100+15
=215(厘米)
215厘米=21.5分米
故答案为:B
【点睛】此题考查的目的是理解掌握长方体的特征,以及长方体棱长总和的计算方法及应用。
13.A
【分析】根据正方体的棱长总和=棱长×12,举例计算即可。
【详解】设一个正方体棱长原来是1,则棱长总和是1×12=12;
一个正方体棱长扩大到原来的2倍就是2,则棱长总和是2×12=24。
则这个正方体的棱长总和扩大到原来的2倍。
故选:A。
【点睛】掌握正方体的棱长总和公式是关键。
14.B
【分析】根据长方体的特征,长方体的六个面都是长方形,有可能相对的两个面是正方形,如果相对的两个面是正方形,这两个面上的8条棱长是相等的,另外4条棱的长度是相等的,用8根5厘米长的小棒和4根3厘米长的小棒,搭成了一个长是5厘米,宽是3厘米,高是5厘米的长方体框架。据此求出这个长方体框架的棱长之和。
【详解】(5+3+5)×4
=13×4
=52(厘米)
故答案为:B
【点睛】本题考查长方体的总棱长,明确搭成长方体的长、宽和高的长度是解题的关键。
15.A
【分析】将正方体展开图复原得到正方体,得到后根据几个字的相对位置去判断与“御”相对的是哪个字。
【详解】假设以“书”所在的面为底,将正方体展开图复原,不难发现,“射”所在的面为后面的面,字“御”和“数”所在的面分别为左、右两个面,字“礼”所在的面为前面的面,那么字“乐”所在的面自然就成为了上面的面。由于左面和右面是相对的,所以与“御”相对的是“数”。
故答案为:A
16.B
【分析】根据生活经验、数据大小及对长度单位的认识,结合长方体的特征可知,书包、数学书、粉笔盒不可能是长25cm,宽10cm,高4cm的长方体,据此选择。
【详解】A.书包的高超过4cm,所以这个物品不可能是书包;
B.文具盒的长约是25cm,宽约是10cm,高约是4cm,所以这个物品可能是文具盒;
C.数学书的高小于4cm,所以这个物品不可能是数学书;
D.粉笔盒的长小于25cm,高大于4cm,所以这个物品不可能是粉笔盒。
故答案为:B
【点睛】本题考查长方体的特征以及根据计量单位和数据的大小,选择合适的物体。
17.√
【分析】长方体有6个面,有三组相对的面完全相同,一般情况下六个面都是长方形,特殊情况时有两个面是正方形,其他四个面都是长方形,并且这四个面完全相同。据此解答即可。
【详解】一个长方体有6个面,其中至少有4个面是长方形。原题说法正确。
故答案为:√
【点睛】此题考查长方体的特征,解题关键是理解有些长方体相对的两个面是正方形。
18.√
【分析】根据长方体的特征,6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面的面积相等。由此解答。
【详解】当长方体的底面是正方形时,它的长与宽是相等的,所以有4个面的面积相等。
故答案为:√。
【点睛】此题主要根据长方体的特征解决问题。
19.√
【分析】有两个相对的面是正方形的长方体,其它四个面的形状完全相同,面积相等,据此解答。
【详解】
如图所示,长方体上面、下面、前面、后面四个面的形状完全相同,则长方体相邻的两个面可能完全相同。
故答案为:√
【点睛】长方体中相对的面形状相同,一个长方体中至少有2个面形状相同,最多有4个面形状相同。
20.√
【分析】长方体一般是由6个长方形(特殊情况有两个相对的面是正方形)围成的立体图形。在一个长方体中,相对的面完全相同。据此解答。
【详解】例如:
长方体的长、宽都是4cm,高是6cm,那么上下面是4×4的正方形,前后面是4×6的长方形,左右面也是4×6的长方形,这4个面完全相同。
所以如果长方体有两个相对的面是正方形,那么其余的4个面完全相同。
故答案为:√
【点睛】掌握长方体的特征是解题的关键。
21.×
【分析】根据长方体的特征是:6个面都是长方形(特殊情况有两个相对的面的正方形),相对的面的面积相等;正方体的特征:正方体的6个面是完全相同的正方形;解答即可。
【详解】由分析可知,长方体的各个面中可能有正方形,正方体的各个面中不可能有长方形。题干说法错误。
故答案为:×
【点睛】此题考查的目的是理解掌握长方体、正方体的特征。
22.见详解
【分析】
观察可知,与1相邻的有4个面,分别出现了2、3、4、6,只有5没出现,所以1的对面是5;与3相邻的有4个面,分别出现了1、4、5、6,只有2没出现,所以3的对面是2;与6相邻的4个面,确定的有2、3、5,与4相邻的4个面,确定的有1、2、3、5,所以4的对面是6。
【详解】由分析可得:与1相对的面上写着5,与3相对的面上写着2,与4相对的面上写着6。
23.2厘米
【详解】解:长方体的周长=4×(长+宽+高),所以高=(周长-4×(长+宽))÷4,所以依此可以列式
[48-(6+4)×4]÷4
=[48-40]÷4,
=8÷4,
=2(厘米),
答:高是2厘米.
【难度】一般
24.4厘米
【分析】长方体12条棱长的总长度是60厘米,12条棱分别为:4条长,4条宽,4条高。60÷4求出的是1条长、一条宽和一条高的长度,从15厘米中去掉长6厘米,宽5厘米,剩下的就是高的长度了。
【详解】60÷4-6-5
=15-6-5
=4(厘米)
答:这个长方体模型的高是4厘米。
【点睛】考查了长方体棱长和的应用,长方体棱长总和=(长+宽+高)×4。
25.最大150cm 最小80cm
【详解】最大:15×10=150(cm ) 最小:10×8=80(cm )
26.320厘米
【分析】通过观察可知,彩带由2条长、6条宽、4条高和打结部分组成,已知礼品盒长35厘米,宽25厘米,高20厘米,则用35×2+25×6+20×4+20即可得彩带的长度。
【详解】35×2+25×6+20×4+20
=70+150+80+20
=320(厘米)
答:这根彩带至少长320厘米。
【点睛】本题考查了长方体棱长和公式的灵活应用,注意彩带由几条长、几条宽和几条高组成。
知识点:
1、长方体各部分的名称:围成长方体的长方形(或正方形)叫做长方体的面,面和面相交的线 段叫做棱,棱和棱的交点叫做顶点。
2、
3、相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高,如图:
长方体有 4 条长,4 条宽和4条高。
4、正方体的 6 个面是完全相同的正方形,12 条棱的长度都相等,有 8 个顶点。正方体是特殊的长方体。
一、填空题
1.魔方是常见的( )体,它有( )个面,( )条棱,8个( )。
2.一个长方体有( )个顶点,有( )个面,这些面都是( )形或( )形。一个长方体中,至少有( )个面是完全相同的。
3.如图,长方体一共有( )条棱,棱长是5cm的棱有( )条,棱长是4cm的棱有( )条,棱长是3cm的棱有( )条,所有棱长的和是( )cm。
4.一个正方体纸盒每个面的周长都是20厘米,它的棱长是( )厘米,棱长总和是( )厘米。
5.用一根长3.6m的铁丝,做成一个长0.4m,宽0.3m的长方体框架,这个框架的高是( )。
6.用铁丝做一个棱长是2dm的正方体框架,至少需要铁丝( )dm。
7.正方体是由6个完全相同的( )围成的立体图形,所有的棱长都( )。
8.用铁丝焊接一个长方体框架,同一顶点上的三根铁丝长分别为18cm,15cm和9cm,一共用( )cm铁丝。
9.在图的长方体中,相交于同一顶点的三条棱长之和是12分米,一只蚂蚁从点A沿着长方体框架的棱爬到点B,至少要爬( )分米。
二、选择题
10.下面选项中,不是正方体展开图的是( )。
A. B. C. D.
11.有一根铁丝,恰好可以围成长6厘米、宽3厘米、高3厘米的长方体框架,这根铁丝恰好也可以围成一个正方体框架,则围成的正方体框架的棱长是( )厘米。
A.1 B.4 C.8 D.16
12.用丝带扎一个礼品盒(如下图所示),接头处长15厘米,捆扎一个礼品盒至少需要( )分米丝带。
A.20 B.21.5 C.22.5 D.23.5
13.若一个正方体棱和扩大到原来的2倍,则这个正方体的棱长总和扩大到原来的( )倍。
A.2 B.8 C.12 D.24
14.小明有10根5厘米长的小棒和6根3厘米长的小棒,他用其中的12根搭成了一个长方体框架,长方体框架的棱长总和是( )厘米。
A.48 B.52 C.56 D.68
15.中国古代的士人学习的“六艺”是“礼、乐、射、御、书、数”。在正方体的6个面上分别写着“六艺”中的一种。正方体展开后如图,与“御”相对的是( )。
A.数 B.乐 C.礼
16.如图是一个长方体物品的长、宽、高,请你根据具体数据估计这可能是( )。
A.书包 B.文具盒 C.数学书 D.粉笔盒
三、判断题
17.一个长方体至少有4个长方形的面。( )
18.底面是正方形的长方体,一定有4个面的面积相等。( )
19.长方体相邻的两个面可能完全相同。( )
20.如果一个长方体有一组相对的面是正方形,则其余四个面完全相同。( )
21.长方体的各个面中可能有正方形,正方体的各个面中可能有长方形。( )
四、解答题
22.如下图,正方体的6个面上分别写着1、2、3、4、5、6。与1相对的面上写着什么数字?与3相对的面上写着什么数字?与4相对的面上写着什么数字?
23.一个长方体的棱长总和是48厘米,长6厘米,宽4厘米,高是多少厘米?
24.科技小组用60厘米的铁丝做一个长方体模型,这个长方体的长是6厘米,宽是5厘米,高是多少厘米?
25.一个长方体纸盒的长、宽、高分别是15cm、8cm、10cm,把它平放在桌面上,它占桌面的最大面积是多少?最小呢?
26.把一个长35厘米,宽25厘米,高20厘米的礼品盒用彩带捆扎起来(如下图所示),打结部分共用了20厘米,这根彩带至少长多少厘米?
参考答案:
1. 正方 6 12 顶点
【分析】由6个完全相同的正方形围成的立体图形叫做正方体,也叫立方体,是特殊的长方体。根据正方体的特征:有6个面,这6个面都是正方形,且面积相等;有12条棱,这些棱的长度都相等;有8个顶点,据此解答。
【详解】魔方是常见的(正方)体,它有(6)个面,(12)条棱,8个(顶点)。
2. 8 6 长方 正方 2
【分析】根据长方体的特征:长方体有8个顶点,有6个面,每个面的形状都是长方形或正方形,在长方形中两个相对的面完全相同,一共有3组这样的面。据此可得出答案。
【详解】一个长方体有8个顶点,有6个面,这些面都是长方形或正方形。一个长方体中,至少有2个面是完全相同的。
3. 12 4 4 4 48
【分析】
长方体有12条棱,相对的四条棱长度相等;按长度可分为三组,每一组有4条棱;根据长方体棱长总和=(长+宽+高)×4,列式计算即可求出棱长总和。
【详解】3×4+4×4+5×4
=12+16+20
=28+20
=48(cm)
长方体一共有12条棱,棱长是5cm的棱有4条,棱长是4cm的棱有4条,棱长是3cm的棱有4条,所有棱长的和是48cm。
4. 5 60
【分析】正方体每个面都是完全一样的正方形,根据正方形边长=周长÷4,即可求出正方体棱长,根据正方体棱长总和=棱长×12,求出棱长总和即可。
【详解】20÷4=5(厘米)
5×12=60(厘米)
它的棱长是5厘米,棱长总和是60厘米。
【点睛】关键是熟悉正方体特征,掌握并灵活运用正方体棱长总和公式。
5.0.2m
【分析】根据题意,可知“(长+宽+高)×4=铁丝的总长度” ,据此用铁丝的总长度除以4可以求出一组长、宽、高的和,再减去长和宽即可求出高。
【详解】3.6÷4-0.4-0.3
=0.9-0.4-0.3
=0.2(m)
【点睛】明确长方体棱长总和与长、宽、高的关系是解答本题的关键。
6.24
【分析】由题意可知,要求的是正方体的总棱长,根据正方体的总棱长=棱长×12,据此可解答。
【详解】2×12=24(分米)
【点睛】本题考查正方体的总棱长,熟记正方体的总棱长公式是关键。
7. 正方形 相等
【分析】正方体的特征:6个面都相等,有12条棱,每条棱都相等;据此解答。
【详解】正方体是由6个完全相同的正方形围成的立体图形,所有的棱长都相等。
故答案为:正方形;相等
【点睛】本题考查了正方体的特点;关键是要掌握正方体的特征并灵活运用。
8.168
【分析】求用了多少铁丝就是求出这个长方体框架的棱长总和,从同一个顶点连接的三条棱是一组长宽高,根据长方体的棱长总和=4×(长+宽+高),代入数据即可求解。
【详解】(18+15+9)×4
=42×4
=168(cm)
【点睛】此题考查长方体的棱长总和公式,意识到同一个顶点连接的三条棱是一组长宽高也是解题的关键。
9.12
【分析】
根据题意可知:蚂蚁从A点沿着一个长方体框架的棱爬到B点,至少应爬一个高、一个长、一个宽,12就是长方体的长宽高的和,据此即可解答。
【详解】在如图的长方体中,相交于同一顶点的三条棱长之和是12分米,一只蚂蚁从点A沿着长方体框架的棱爬到点B,至少要爬12分米。
10.D
【分析】正方体的十一种展开图可记忆口诀:一三二,一四一,一在同层可任意,两个三,日状连,三个二,成阶梯,相邻必有日,整体没有田。据此解答。
【详解】A.根据口诀可知,一行有4个的,只能是一四一,所以A符合;
B.根据口诀可知,一行有3个的,可以是一三二,且没有“田”字状,所以B符合;
C.根据口诀可知,三个二成阶梯, 且没有“田”字状,所以C符合;
D.根据口诀可知,一行有4个的,只能是一四一,且一和一不能相连,所以D不符合。
故答案为:D
【点睛】本题主要考查的是正方体的展开图,培养学生的空间想象能力。
11.B
【分析】根据长方体的总棱长公式:L=(a+b+h)×4,据此求出铁丝的长度,铁丝的长度也是正方体框架的总棱长,再根据正方体的总棱长公式:L=12a,用铁丝的长度除以12即可求出正方体框架的棱长。
【详解】(6+3+3)×4
=12×4
=48(厘米)
48÷12=4(厘米)
则围成的正方体框架的棱长是4厘米。
故答案为:B
12.B
【分析】通过观察图形可知,捆扎这个礼品盒需要丝带的长度等于这个长方体的两条长加两条宽加4条高再加上接头处用的15厘米,据此列式解答。
【详解】30×2+20×2+25×4+15
=60+40+100+15
=100+100+15
=215(厘米)
215厘米=21.5分米
故答案为:B
【点睛】此题考查的目的是理解掌握长方体的特征,以及长方体棱长总和的计算方法及应用。
13.A
【分析】根据正方体的棱长总和=棱长×12,举例计算即可。
【详解】设一个正方体棱长原来是1,则棱长总和是1×12=12;
一个正方体棱长扩大到原来的2倍就是2,则棱长总和是2×12=24。
则这个正方体的棱长总和扩大到原来的2倍。
故选:A。
【点睛】掌握正方体的棱长总和公式是关键。
14.B
【分析】根据长方体的特征,长方体的六个面都是长方形,有可能相对的两个面是正方形,如果相对的两个面是正方形,这两个面上的8条棱长是相等的,另外4条棱的长度是相等的,用8根5厘米长的小棒和4根3厘米长的小棒,搭成了一个长是5厘米,宽是3厘米,高是5厘米的长方体框架。据此求出这个长方体框架的棱长之和。
【详解】(5+3+5)×4
=13×4
=52(厘米)
故答案为:B
【点睛】本题考查长方体的总棱长,明确搭成长方体的长、宽和高的长度是解题的关键。
15.A
【分析】将正方体展开图复原得到正方体,得到后根据几个字的相对位置去判断与“御”相对的是哪个字。
【详解】假设以“书”所在的面为底,将正方体展开图复原,不难发现,“射”所在的面为后面的面,字“御”和“数”所在的面分别为左、右两个面,字“礼”所在的面为前面的面,那么字“乐”所在的面自然就成为了上面的面。由于左面和右面是相对的,所以与“御”相对的是“数”。
故答案为:A
16.B
【分析】根据生活经验、数据大小及对长度单位的认识,结合长方体的特征可知,书包、数学书、粉笔盒不可能是长25cm,宽10cm,高4cm的长方体,据此选择。
【详解】A.书包的高超过4cm,所以这个物品不可能是书包;
B.文具盒的长约是25cm,宽约是10cm,高约是4cm,所以这个物品可能是文具盒;
C.数学书的高小于4cm,所以这个物品不可能是数学书;
D.粉笔盒的长小于25cm,高大于4cm,所以这个物品不可能是粉笔盒。
故答案为:B
【点睛】本题考查长方体的特征以及根据计量单位和数据的大小,选择合适的物体。
17.√
【分析】长方体有6个面,有三组相对的面完全相同,一般情况下六个面都是长方形,特殊情况时有两个面是正方形,其他四个面都是长方形,并且这四个面完全相同。据此解答即可。
【详解】一个长方体有6个面,其中至少有4个面是长方形。原题说法正确。
故答案为:√
【点睛】此题考查长方体的特征,解题关键是理解有些长方体相对的两个面是正方形。
18.√
【分析】根据长方体的特征,6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面的面积相等。由此解答。
【详解】当长方体的底面是正方形时,它的长与宽是相等的,所以有4个面的面积相等。
故答案为:√。
【点睛】此题主要根据长方体的特征解决问题。
19.√
【分析】有两个相对的面是正方形的长方体,其它四个面的形状完全相同,面积相等,据此解答。
【详解】
如图所示,长方体上面、下面、前面、后面四个面的形状完全相同,则长方体相邻的两个面可能完全相同。
故答案为:√
【点睛】长方体中相对的面形状相同,一个长方体中至少有2个面形状相同,最多有4个面形状相同。
20.√
【分析】长方体一般是由6个长方形(特殊情况有两个相对的面是正方形)围成的立体图形。在一个长方体中,相对的面完全相同。据此解答。
【详解】例如:
长方体的长、宽都是4cm,高是6cm,那么上下面是4×4的正方形,前后面是4×6的长方形,左右面也是4×6的长方形,这4个面完全相同。
所以如果长方体有两个相对的面是正方形,那么其余的4个面完全相同。
故答案为:√
【点睛】掌握长方体的特征是解题的关键。
21.×
【分析】根据长方体的特征是:6个面都是长方形(特殊情况有两个相对的面的正方形),相对的面的面积相等;正方体的特征:正方体的6个面是完全相同的正方形;解答即可。
【详解】由分析可知,长方体的各个面中可能有正方形,正方体的各个面中不可能有长方形。题干说法错误。
故答案为:×
【点睛】此题考查的目的是理解掌握长方体、正方体的特征。
22.见详解
【分析】
观察可知,与1相邻的有4个面,分别出现了2、3、4、6,只有5没出现,所以1的对面是5;与3相邻的有4个面,分别出现了1、4、5、6,只有2没出现,所以3的对面是2;与6相邻的4个面,确定的有2、3、5,与4相邻的4个面,确定的有1、2、3、5,所以4的对面是6。
【详解】由分析可得:与1相对的面上写着5,与3相对的面上写着2,与4相对的面上写着6。
23.2厘米
【详解】解:长方体的周长=4×(长+宽+高),所以高=(周长-4×(长+宽))÷4,所以依此可以列式
[48-(6+4)×4]÷4
=[48-40]÷4,
=8÷4,
=2(厘米),
答:高是2厘米.
【难度】一般
24.4厘米
【分析】长方体12条棱长的总长度是60厘米,12条棱分别为:4条长,4条宽,4条高。60÷4求出的是1条长、一条宽和一条高的长度,从15厘米中去掉长6厘米,宽5厘米,剩下的就是高的长度了。
【详解】60÷4-6-5
=15-6-5
=4(厘米)
答:这个长方体模型的高是4厘米。
【点睛】考查了长方体棱长和的应用,长方体棱长总和=(长+宽+高)×4。
25.最大150cm 最小80cm
【详解】最大:15×10=150(cm ) 最小:10×8=80(cm )
26.320厘米
【分析】通过观察可知,彩带由2条长、6条宽、4条高和打结部分组成,已知礼品盒长35厘米,宽25厘米,高20厘米,则用35×2+25×6+20×4+20即可得彩带的长度。
【详解】35×2+25×6+20×4+20
=70+150+80+20
=320(厘米)
答:这根彩带至少长320厘米。
【点睛】本题考查了长方体棱长和公式的灵活应用,注意彩带由几条长、几条宽和几条高组成。
