18.1.1.1 平行四边形边、角的性质同步练习(含答案)
文档属性
| 名称 | 18.1.1.1 平行四边形边、角的性质同步练习(含答案) | 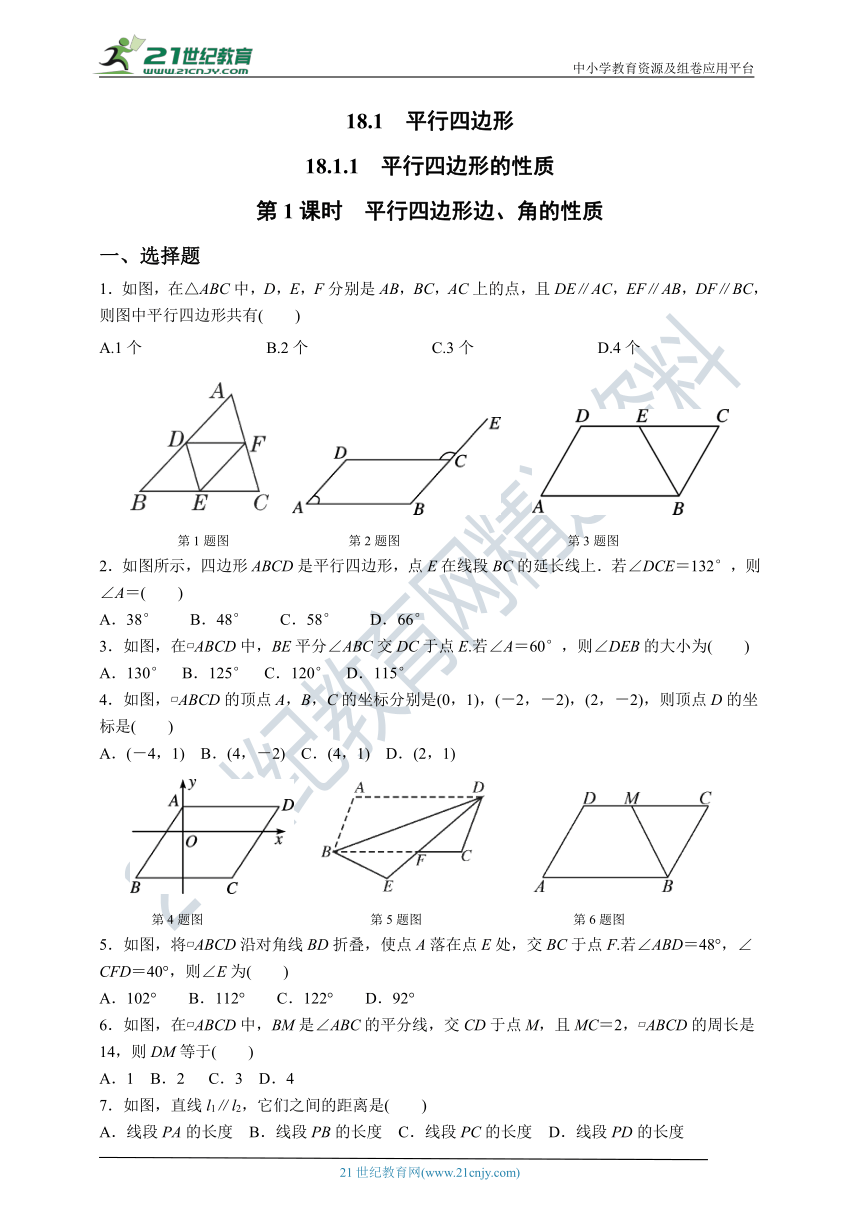 | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-04 21:50:23 | ||
图片预览




文档简介
18.1 平行四边形
18.1.1 平行四边形的性质
第1课时 平行四边形边、角的性质
一、选择题
1.如图,在△ABC中,D,E,F分别是AB,BC,AC上的点,且DE∥AC,EF∥AB,DF∥BC,则图中平行四边形共有( )
A.1个 B.2个 C.3个 D.4个
第1题图 第2题图 第3题图
2.如图所示,四边形ABCD是平行四边形,点E在线段BC的延长线上.若∠DCE=132°,则∠A=( )
A.38° B.48° C.58° D.66°
3.如图,在 ABCD中,BE平分∠ABC交DC于点E.若∠A=60°,则∠DEB的大小为( )
A.130° B.125° C.120° D.115°
4.如图, ABCD的顶点A,B,C的坐标分别是(0,1),(-2,-2),(2,-2),则顶点D的坐标是( )
A.(-4,1) B.(4,-2) C.(4,1) D.(2,1)
第4题图 第5题图 第6题图
5.如图,将 ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F.若∠ABD=48°,∠CFD=40°,则∠E为( )
A.102° B.112° C.122° D.92°
6.如图,在 ABCD中,BM是∠ABC的平分线,交CD于点M,且MC=2, ABCD的周长是14,则DM等于( )
A.1 B.2 C.3 D.4
7.如图,直线l1∥l2,它们之间的距离是( )
A.线段PA的长度 B.线段PB的长度 C.线段PC的长度 D.线段PD的长度
第7题图 第8题图 第9题图
8.如图,将一副三角板在平行四边形ABCD中作如下摆放,设∠1=30°,那么∠2=( )
A.55° B.65° C.75° D.85°
9.如图,在 ABCD中,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F.若AB=3,AD=4,则EF的长是( )
A.1 B.2 C.2.5 D.3
10.如图,在平行四边形ABCD中,将△ABC沿着AC所在的直线折叠得到△AB′C,B′C交AD于点E,连接B′D,若∠B=60°,∠ACB=45°,AC=,则B′D的长是( )
A.1 B. C. D.
第10题图 第11题图 第15题图
二、填空题
11.如图,在 ABCD中,BD=CD,AE⊥BD于点E,若∠C=70°,则∠BAE= °.
12.设AB,CD,EF是同一平面内三条互相平行的直线,已知AB与CD的距离是12 cm,EF与CD的距离是5 cm,则AB与EF的距离等于 cm.
13.四边形ABCD是平行四边形,AB=6,∠BAD的平分线交直线BC于点E.若CE=2,则 ABCD的周长为 .
14.如图,两条平行线之间的三个图形,图 的面积最大,图 的面积最小.
15.如图,将 ABCD沿对角线BD折叠,使点A落在点E处,ED交BC于点F.若∠ABD为48°,∠CFD=40°,则∠E的度数为 °.
三、解答题
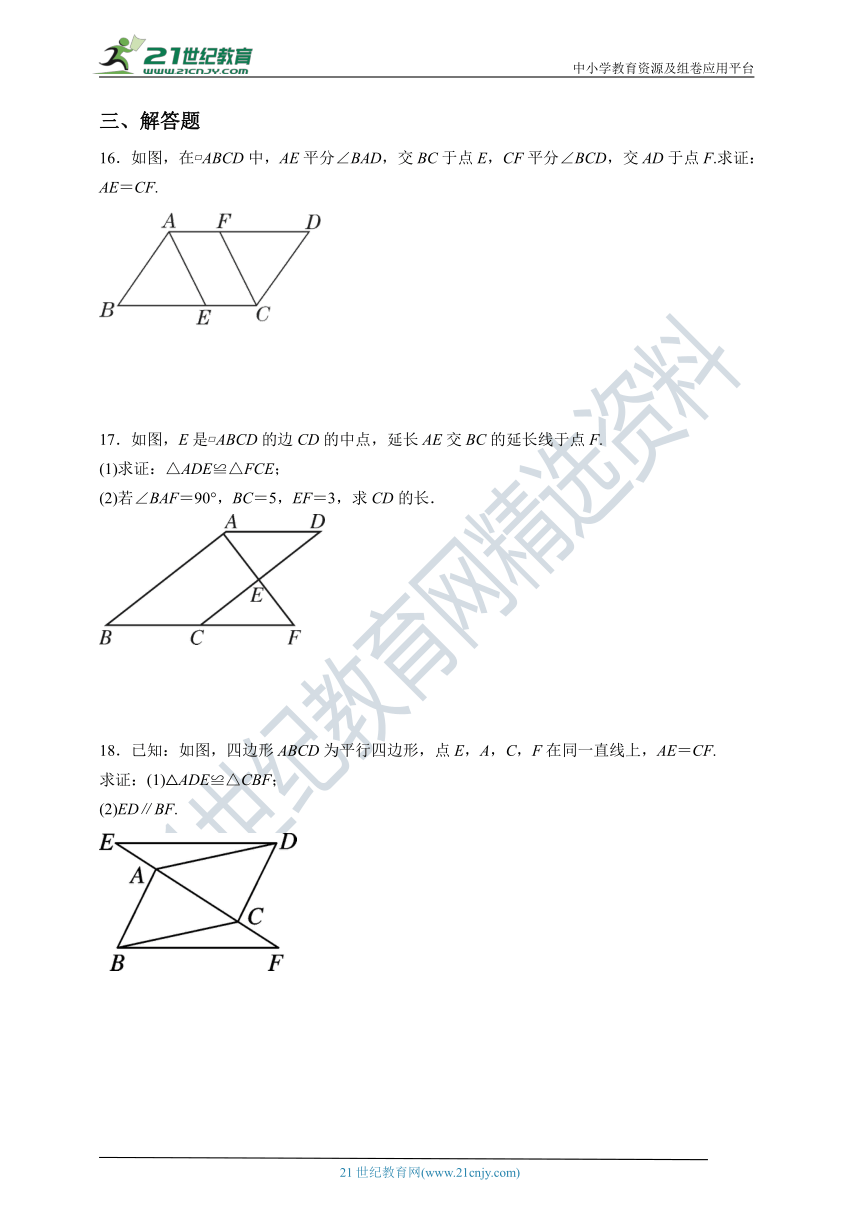
16.如图,在 ABCD中,AE平分∠BAD,交BC于点E,CF平分∠BCD,交AD于点F.求证:AE=CF.
17.如图,E是 ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.
18.已知:如图,四边形ABCD为平行四边形,点E,A,C,F在同一直线上,AE=CF.
求证:(1)△ADE≌△CBF;
(2)ED∥BF.
19.如图, ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
20.如图,在平行四边形ABCD中,E为BC边上一点,且AB=AE.
(1)求证:∠ACB=∠EDA;
(2)若AB=5,BE=6,EC=1,求DE的长.
21.如图,分别以 ABCD(∠CDA≠90°)的三边AB,CD,DA为斜边作等腰直角三角形,得到△ABE,△CDG,△ADF.
(1)如图①,当三个等腰直角三角形都在该平行四边形外部时,连接GF,EF. 请判断GF与EF的关系.
(2)如图②,当三个等腰直角三角形都在该平行四边形内部时,连接GF,EF,(1)中结论还成立吗?若成立,请给出证明;若不成立,请说明理由.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.如图,在△ABC中,D,E,F分别是AB,BC,AC上的点,且DE∥AC,EF∥AB,DF∥BC,则图中平行四边形共有( C )
A.1个 B.2个 C.3个 D.4个
【解析】∵DE∥AC,EF∥AB,DF∥BC,∴图中的平行四边形有 ADEF, BEFD, DECF.
第1题图 第2题图 第3题图
2.如图所示,四边形ABCD是平行四边形,点E在线段BC的延长线上.若∠DCE=132°,则∠A=( B )
A.38° B.48° C.58° D.66°
3.如图,在 ABCD中,BE平分∠ABC交DC于点E.若∠A=60°,则∠DEB的大小为( C )
A.130° B.125° C.120° D.115°
4.如图, ABCD的顶点A,B,C的坐标分别是(0,1),(-2,-2),(2,-2),则顶点D的坐标是( C )
A.(-4,1) B.(4,-2) C.(4,1) D.(2,1)
第4题图 第5题图 第6题图
5.如图,将 ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F.若∠ABD=48°,∠CFD=40°,则∠E为( B )
A.102° B.112° C.122° D.92°
6.如图,在 ABCD中,BM是∠ABC的平分线,交CD于点M,且MC=2, ABCD的周长是14,则DM等于( C )
A.1 B.2 C.3 D.4
7.如图,直线l1∥l2,它们之间的距离是( B )
A.线段PA的长度 B.线段PB的长度 C.线段PC的长度 D.线段PD的长度
第7题图 第8题图 第9题图
8.如图,将一副三角板在平行四边形ABCD中作如下摆放,设∠1=30°,那么∠2=( C )
A.55° B.65° C.75° D.85°
9.如图,在 ABCD中,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F.若AB=3,AD=4,则EF的长是( B )
A.1 B.2 C.2.5 D.3
10.如图,在平行四边形ABCD中,将△ABC沿着AC所在的直线折叠得到△AB′C,B′C交AD于点E,连接B′D,若∠B=60°,∠ACB=45°,AC=,则B′D的长是( B )
A.1 B. C. D.
【解析】∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∠ADC=60°,∴∠CAE=∠ACB=45°,∵将△ABC沿AC翻折至△AB′C,∴∠ACB′=∠ACB=45°,∠AB′C=∠B=60°,∴∠AEC=180°-∠CAE-∠ACB′=90°,∴AE=CE=,∵∠AEC=90°,∠AB′C=60°,∠ADC=60°,∴∠B′AD=30°,∠DCE=30°,∴B′E=DE=1,∴B′D==.
第10题图 第11题图 第15题图
二、填空题
11.如图,在 ABCD中,BD=CD,AE⊥BD于点E,若∠C=70°,则∠BAE= °.
【答案】50
12.设AB,CD,EF是同一平面内三条互相平行的直线,已知AB与CD的距离是12 cm,EF与CD的距离是5 cm,则AB与EF的距离等于 cm.
【答案】7或17
13.四边形ABCD是平行四边形,AB=6,∠BAD的平分线交直线BC于点E.若CE=2,则 ABCD的周长为 .
【答案】20或28
14.如图,两条平行线之间的三个图形,图 的面积最大,图 的面积最小.
【答案】③ ②
15.如图,将 ABCD沿对角线BD折叠,使点A落在点E处,ED交BC于点F.若∠ABD为48°,∠CFD=40°,则∠E的度数为 °.
【答案】112
三、解答题
16.如图,在 ABCD中,AE平分∠BAD,交BC于点E,CF平分∠BCD,交AD于点F.求证:AE=CF.
【证明】∵四边形ABCD是平行四边形,∴AB=CD,∠B=∠D,∠BAD=∠BCD.
∵AE平分∠BAD,CF平分∠BCD,
∴∠BAE=∠BAD,∠FCD=∠BCD.
∴∠BAE=∠FCD.
∴△ABE≌△CDF(ASA).∴AE=CF.
17.如图,E是 ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.
(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAE=∠F,∠D=∠ECF.∵E是CD的中点,∴DE=CE.在△ADE和△FCE中,,∴△ADE≌△FCE(AAS);
(2)解:∵△ADE≌△FCE,∴AE=EF=3.∵AB∥CD,∴∠AED=∠BAF=90°.在Rt△ADE中,AD=BC=5,∴DE===4,∴CD=2DE=8.
18.已知:如图,四边形ABCD为平行四边形,点E,A,C,F在同一直线上,AE=CF.
求证:(1)△ADE≌△CBF;
(2)ED∥BF.
证明:(1)∵四边形ABCD为平行四边形,
∴DA=BC,DA∥BC,∴∠DAC=∠BCA,
∵∠DAC+∠EAD=180°,∠BCA+∠FCB=180°,
∴∠EAD=∠FCB,
在△ADE和△CBF中,
∴△ADE≌△CBF(SAS).
(2)由(1)知,△ADE≌△CBF,
∴∠E=∠F,∴ED∥BF.
19.如图, ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠CDB=∠ABD.在△BOE与△DOF中,∵,∴△BOE≌△DOF(AAS),∴BO=DO;
(2)解:∵EF⊥AB,∴∠FEA=90°.∵AB∥CD,∴∠GDF=∠A=45°,∠GFD=∠FEA=90°,∴∠G=45°,∴DF=FG=1,∴DG==.∵∠BDG=90°,∠G=45°,∴∠GOD=45°,∴∠GOD=∠G,故DO=BO=DG=,∴BD=2,∵∠A=45°,∠ADB=90°,∴AD=BD=2.
20.如图,在平行四边形ABCD中,E为BC边上一点,且AB=AE.
(1)求证:∠ACB=∠EDA;
(2)若AB=5,BE=6,EC=1,求DE的长.
解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,∴∠AEB=∠EAD,
∵AB=AE,∴∠B=∠AEB,∴∠B=∠EAD,
在△ABC和△EAD中,
∴△ABC≌△EAD(SAS),
∴∠ACB=∠EDA.
(2)如图,过点A作AF⊥BC于点F,
∵AB=AE,AB=5,BE=6,EC=1,
∴BF=EF=BE=3,FC=FE+EC=4,
在Rt△ABF和Rt△AFC中,
由勾股定理,得AF==4,
AC==4 ,
由(1)得△ABC≌△EAD,∴DE=AC=4 .
21.如图,分别以 ABCD(∠CDA≠90°)的三边AB,CD,DA为斜边作等腰直角三角形,得到△ABE,△CDG,△ADF.
(1)如图①,当三个等腰直角三角形都在该平行四边形外部时,连接GF,EF. 请判断GF与EF的关系.
(2)如图②,当三个等腰直角三角形都在该平行四边形内部时,连接GF,EF,(1)中结论还成立吗?若成立,请给出证明;若不成立,请说明理由.
【解】(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,∴∠DAB+∠ADC=180°.
∵△ABE,△CDG,△ADF都是等腰直角三角形,CD=AB,
∴DG=CG=AE=BE,DF=AF,∠CDG=∠ADF=∠BAE=45°,
∴∠GDF=∠GDC+∠CDA+∠ADF=90°+∠CDA,∠EAF=360°-∠BAE-∠DAF-∠BAD=270°-(180°-∠CDA)=90°+∠CDA,∴∠FDG=∠EAF.
∴△EAF≌△GDF(SAS),∴EF=FG,∠EFA=∠GFD,
∴∠GFD+∠GFA=∠EFA+∠GFA=90°,
∴∠GFE=90°,∴GF⊥EF.
(2)GF⊥EF,GF=EF仍然成立.证明如下:
∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠DAB+∠ADC=180°.
∵△ABE,△CDG,△ADF都是等腰直角三角形,
∴DG=CG=AE=BE,DF=AF,∠CDG=∠ADF=∠FAD=∠BAE=45°.
∵∠BAE+∠DAF+∠EAF+∠ADF+∠FDC=180°,
∴∠EAF+∠CDF=45°.
∵∠CDF+∠GDF=∠CDG=45°,
∴∠FDG=∠EAF.
∴△GDF≌△EAF(SAS),
∴EF=FG,∠EFA=∠GFD,∴∠EFA+∠GFA=∠GFD+∠GFA=90°,
∴∠GFE=90°,∴GF⊥EF.
18.1.1 平行四边形的性质
第1课时 平行四边形边、角的性质
一、选择题
1.如图,在△ABC中,D,E,F分别是AB,BC,AC上的点,且DE∥AC,EF∥AB,DF∥BC,则图中平行四边形共有( )
A.1个 B.2个 C.3个 D.4个
第1题图 第2题图 第3题图
2.如图所示,四边形ABCD是平行四边形,点E在线段BC的延长线上.若∠DCE=132°,则∠A=( )
A.38° B.48° C.58° D.66°
3.如图,在 ABCD中,BE平分∠ABC交DC于点E.若∠A=60°,则∠DEB的大小为( )
A.130° B.125° C.120° D.115°
4.如图, ABCD的顶点A,B,C的坐标分别是(0,1),(-2,-2),(2,-2),则顶点D的坐标是( )
A.(-4,1) B.(4,-2) C.(4,1) D.(2,1)
第4题图 第5题图 第6题图
5.如图,将 ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F.若∠ABD=48°,∠CFD=40°,则∠E为( )
A.102° B.112° C.122° D.92°
6.如图,在 ABCD中,BM是∠ABC的平分线,交CD于点M,且MC=2, ABCD的周长是14,则DM等于( )
A.1 B.2 C.3 D.4
7.如图,直线l1∥l2,它们之间的距离是( )
A.线段PA的长度 B.线段PB的长度 C.线段PC的长度 D.线段PD的长度
第7题图 第8题图 第9题图
8.如图,将一副三角板在平行四边形ABCD中作如下摆放,设∠1=30°,那么∠2=( )
A.55° B.65° C.75° D.85°
9.如图,在 ABCD中,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F.若AB=3,AD=4,则EF的长是( )
A.1 B.2 C.2.5 D.3
10.如图,在平行四边形ABCD中,将△ABC沿着AC所在的直线折叠得到△AB′C,B′C交AD于点E,连接B′D,若∠B=60°,∠ACB=45°,AC=,则B′D的长是( )
A.1 B. C. D.
第10题图 第11题图 第15题图
二、填空题
11.如图,在 ABCD中,BD=CD,AE⊥BD于点E,若∠C=70°,则∠BAE= °.
12.设AB,CD,EF是同一平面内三条互相平行的直线,已知AB与CD的距离是12 cm,EF与CD的距离是5 cm,则AB与EF的距离等于 cm.
13.四边形ABCD是平行四边形,AB=6,∠BAD的平分线交直线BC于点E.若CE=2,则 ABCD的周长为 .
14.如图,两条平行线之间的三个图形,图 的面积最大,图 的面积最小.
15.如图,将 ABCD沿对角线BD折叠,使点A落在点E处,ED交BC于点F.若∠ABD为48°,∠CFD=40°,则∠E的度数为 °.
三、解答题
16.如图,在 ABCD中,AE平分∠BAD,交BC于点E,CF平分∠BCD,交AD于点F.求证:AE=CF.
17.如图,E是 ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.
18.已知:如图,四边形ABCD为平行四边形,点E,A,C,F在同一直线上,AE=CF.
求证:(1)△ADE≌△CBF;
(2)ED∥BF.
19.如图, ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
20.如图,在平行四边形ABCD中,E为BC边上一点,且AB=AE.
(1)求证:∠ACB=∠EDA;
(2)若AB=5,BE=6,EC=1,求DE的长.
21.如图,分别以 ABCD(∠CDA≠90°)的三边AB,CD,DA为斜边作等腰直角三角形,得到△ABE,△CDG,△ADF.
(1)如图①,当三个等腰直角三角形都在该平行四边形外部时,连接GF,EF. 请判断GF与EF的关系.
(2)如图②,当三个等腰直角三角形都在该平行四边形内部时,连接GF,EF,(1)中结论还成立吗?若成立,请给出证明;若不成立,请说明理由.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.如图,在△ABC中,D,E,F分别是AB,BC,AC上的点,且DE∥AC,EF∥AB,DF∥BC,则图中平行四边形共有( C )
A.1个 B.2个 C.3个 D.4个
【解析】∵DE∥AC,EF∥AB,DF∥BC,∴图中的平行四边形有 ADEF, BEFD, DECF.
第1题图 第2题图 第3题图
2.如图所示,四边形ABCD是平行四边形,点E在线段BC的延长线上.若∠DCE=132°,则∠A=( B )
A.38° B.48° C.58° D.66°
3.如图,在 ABCD中,BE平分∠ABC交DC于点E.若∠A=60°,则∠DEB的大小为( C )
A.130° B.125° C.120° D.115°
4.如图, ABCD的顶点A,B,C的坐标分别是(0,1),(-2,-2),(2,-2),则顶点D的坐标是( C )
A.(-4,1) B.(4,-2) C.(4,1) D.(2,1)
第4题图 第5题图 第6题图
5.如图,将 ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F.若∠ABD=48°,∠CFD=40°,则∠E为( B )
A.102° B.112° C.122° D.92°
6.如图,在 ABCD中,BM是∠ABC的平分线,交CD于点M,且MC=2, ABCD的周长是14,则DM等于( C )
A.1 B.2 C.3 D.4
7.如图,直线l1∥l2,它们之间的距离是( B )
A.线段PA的长度 B.线段PB的长度 C.线段PC的长度 D.线段PD的长度
第7题图 第8题图 第9题图
8.如图,将一副三角板在平行四边形ABCD中作如下摆放,设∠1=30°,那么∠2=( C )
A.55° B.65° C.75° D.85°
9.如图,在 ABCD中,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F.若AB=3,AD=4,则EF的长是( B )
A.1 B.2 C.2.5 D.3
10.如图,在平行四边形ABCD中,将△ABC沿着AC所在的直线折叠得到△AB′C,B′C交AD于点E,连接B′D,若∠B=60°,∠ACB=45°,AC=,则B′D的长是( B )
A.1 B. C. D.
【解析】∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∠ADC=60°,∴∠CAE=∠ACB=45°,∵将△ABC沿AC翻折至△AB′C,∴∠ACB′=∠ACB=45°,∠AB′C=∠B=60°,∴∠AEC=180°-∠CAE-∠ACB′=90°,∴AE=CE=,∵∠AEC=90°,∠AB′C=60°,∠ADC=60°,∴∠B′AD=30°,∠DCE=30°,∴B′E=DE=1,∴B′D==.
第10题图 第11题图 第15题图
二、填空题
11.如图,在 ABCD中,BD=CD,AE⊥BD于点E,若∠C=70°,则∠BAE= °.
【答案】50
12.设AB,CD,EF是同一平面内三条互相平行的直线,已知AB与CD的距离是12 cm,EF与CD的距离是5 cm,则AB与EF的距离等于 cm.
【答案】7或17
13.四边形ABCD是平行四边形,AB=6,∠BAD的平分线交直线BC于点E.若CE=2,则 ABCD的周长为 .
【答案】20或28
14.如图,两条平行线之间的三个图形,图 的面积最大,图 的面积最小.
【答案】③ ②
15.如图,将 ABCD沿对角线BD折叠,使点A落在点E处,ED交BC于点F.若∠ABD为48°,∠CFD=40°,则∠E的度数为 °.
【答案】112
三、解答题
16.如图,在 ABCD中,AE平分∠BAD,交BC于点E,CF平分∠BCD,交AD于点F.求证:AE=CF.
【证明】∵四边形ABCD是平行四边形,∴AB=CD,∠B=∠D,∠BAD=∠BCD.
∵AE平分∠BAD,CF平分∠BCD,
∴∠BAE=∠BAD,∠FCD=∠BCD.
∴∠BAE=∠FCD.
∴△ABE≌△CDF(ASA).∴AE=CF.
17.如图,E是 ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.
(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAE=∠F,∠D=∠ECF.∵E是CD的中点,∴DE=CE.在△ADE和△FCE中,,∴△ADE≌△FCE(AAS);
(2)解:∵△ADE≌△FCE,∴AE=EF=3.∵AB∥CD,∴∠AED=∠BAF=90°.在Rt△ADE中,AD=BC=5,∴DE===4,∴CD=2DE=8.
18.已知:如图,四边形ABCD为平行四边形,点E,A,C,F在同一直线上,AE=CF.
求证:(1)△ADE≌△CBF;
(2)ED∥BF.
证明:(1)∵四边形ABCD为平行四边形,
∴DA=BC,DA∥BC,∴∠DAC=∠BCA,
∵∠DAC+∠EAD=180°,∠BCA+∠FCB=180°,
∴∠EAD=∠FCB,
在△ADE和△CBF中,
∴△ADE≌△CBF(SAS).
(2)由(1)知,△ADE≌△CBF,
∴∠E=∠F,∴ED∥BF.
19.如图, ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠CDB=∠ABD.在△BOE与△DOF中,∵,∴△BOE≌△DOF(AAS),∴BO=DO;
(2)解:∵EF⊥AB,∴∠FEA=90°.∵AB∥CD,∴∠GDF=∠A=45°,∠GFD=∠FEA=90°,∴∠G=45°,∴DF=FG=1,∴DG==.∵∠BDG=90°,∠G=45°,∴∠GOD=45°,∴∠GOD=∠G,故DO=BO=DG=,∴BD=2,∵∠A=45°,∠ADB=90°,∴AD=BD=2.
20.如图,在平行四边形ABCD中,E为BC边上一点,且AB=AE.
(1)求证:∠ACB=∠EDA;
(2)若AB=5,BE=6,EC=1,求DE的长.
解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,∴∠AEB=∠EAD,
∵AB=AE,∴∠B=∠AEB,∴∠B=∠EAD,
在△ABC和△EAD中,
∴△ABC≌△EAD(SAS),
∴∠ACB=∠EDA.
(2)如图,过点A作AF⊥BC于点F,
∵AB=AE,AB=5,BE=6,EC=1,
∴BF=EF=BE=3,FC=FE+EC=4,
在Rt△ABF和Rt△AFC中,
由勾股定理,得AF==4,
AC==4 ,
由(1)得△ABC≌△EAD,∴DE=AC=4 .
21.如图,分别以 ABCD(∠CDA≠90°)的三边AB,CD,DA为斜边作等腰直角三角形,得到△ABE,△CDG,△ADF.
(1)如图①,当三个等腰直角三角形都在该平行四边形外部时,连接GF,EF. 请判断GF与EF的关系.
(2)如图②,当三个等腰直角三角形都在该平行四边形内部时,连接GF,EF,(1)中结论还成立吗?若成立,请给出证明;若不成立,请说明理由.
【解】(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,∴∠DAB+∠ADC=180°.
∵△ABE,△CDG,△ADF都是等腰直角三角形,CD=AB,
∴DG=CG=AE=BE,DF=AF,∠CDG=∠ADF=∠BAE=45°,
∴∠GDF=∠GDC+∠CDA+∠ADF=90°+∠CDA,∠EAF=360°-∠BAE-∠DAF-∠BAD=270°-(180°-∠CDA)=90°+∠CDA,∴∠FDG=∠EAF.
∴△EAF≌△GDF(SAS),∴EF=FG,∠EFA=∠GFD,
∴∠GFD+∠GFA=∠EFA+∠GFA=90°,
∴∠GFE=90°,∴GF⊥EF.
(2)GF⊥EF,GF=EF仍然成立.证明如下:
∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠DAB+∠ADC=180°.
∵△ABE,△CDG,△ADF都是等腰直角三角形,
∴DG=CG=AE=BE,DF=AF,∠CDG=∠ADF=∠FAD=∠BAE=45°.
∵∠BAE+∠DAF+∠EAF+∠ADF+∠FDC=180°,
∴∠EAF+∠CDF=45°.
∵∠CDF+∠GDF=∠CDG=45°,
∴∠FDG=∠EAF.
∴△GDF≌△EAF(SAS),
∴EF=FG,∠EFA=∠GFD,∴∠EFA+∠GFA=∠GFD+∠GFA=90°,
∴∠GFE=90°,∴GF⊥EF.
