18.1.2.1 平行四边形的判定同步练习(含答案)
文档属性
| 名称 | 18.1.2.1 平行四边形的判定同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-04 21:53:49 | ||
图片预览


文档简介
18.1 平行四边形
18.1.2 平行四边形的判定
第1课时 平行四边形的判定
一、选择题
1.下面给出了四边形ABCD中∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的是( )
A.1∶2∶3∶4 B.2∶2∶3∶3 C.2∶3∶2∶3 D.2∶3∶3∶2
2.不能判定四边形ABCD为平行四边形的条件是( )
A.AB=CD,AD=BC B.AB=CD,AB∥CD
C.AB=CD,AD∥BC D.AD=BC,AD∥BC
3.在四边形ABCD中,AD∥BC,若四边形ABCD是平行四边形,则还需要满足( )
A.∠A+∠B=180° B.∠A+∠C=180° C.∠B+∠C=180° D.∠B+∠D=180°
4.如图,在四边形ABCD中,AB=CD,BC=AD.若∠B=110°,则∠A的度数为( )
A.110° B.80° C.70° D.90°
第4题图 第5题图 第6题图
5.如图,四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,添加下列条件后仍无法判定四边形ABCD是平行四边形的是( )
A.AB=CD B.AB∥CD C.OB=OD D.∠ADB=∠CBD
6.如图,AB=CD=EF,且△ACE≌△BDF,则图中平行四边形的个数为( )
A.1 B.2 C.3 D.4
7.在四边形ABCD中:①AB∥CD;②AD∥BC;③AB=CD;④AD=BC,从以上选择两个条件使四边形ABCD为平行四边形的选法共有( )
A.3种 B.4种 C.5种 D.6种
8.在平面直角坐标系中,已知点A(0,0),B(2,2),C(3,0),若以点A,B,C,D为顶点的四边形是平行四边形,则点D的坐标不可能为( )
A.(-1,2) B.(5,2) C.(1,-2) D.(2,-2)
9.四边形的四边长分别是a,b,c,d,其中a,c是对边,且满足a2+b2+c2+d2=2ac+2bd,则这个四边形是( )
A.任意四边形 B.四边都相等的四边形
C.对角线互相垂直的四边形 D.平行四边形
10.如图,等边△ABC的边长为6 cm,射线AG∥BC,点E从点A出发沿射线AG以1 cm/s的速度运动,点F从点B出发沿射线BC以2 cm/s的速度运动.设运动时间为t(s),当以A,C,E,F为顶点的四边形是平行四边形时,运动时间t为( )
A.1 s或2 s B.2 s或3 s C.2 s或4 s D.2 s或6 s
第10题图 第11题图 第12题图
二、填空题
11.在如图的网格中,以格点A,B,C,D,E,F中的4个点为顶点,能画出平行四边形的个数为 .
12.如图,在梯形ABCD中,AD∥BC,∠B=50°,∠C=80°,AE∥CD交BC于点E,若AD=2,BC=5,则边CD的长是 .
13.如图,在 ABCD中,E,F分别是边BC,AD上的点,①AE∥CF;②BE=FD;③∠1=∠2;④AE=CF,若要添加其中一个条件,使四边形AECF一定是平行四边形,则添加的条件可以是 .(填序号)
第13题图 第14题图
14.如图,将等边三角形的三条边分别8等分,按顺时针方向(图中箭头方向)标注等分点的序号0,1,2,3,4,5,6,7,8,将不同边上的序号和为8的两点依次连接起来,这样就建立了“三角形”坐标系,在建立的“三角形”坐标系内,每一点的坐标用过这一点且平行(或重合)于原三角形三条边的直线与三边交点的序号来表示(水平方向开始,按顺时针方向),如点A的坐标可表示为(1,2,5),点B的坐标可表示为(3,1,4).
(1)按此方法,则点C的坐标可表示为 ,点D的坐标可表示为 ;
(2)若P点的坐标为(3,m,m-1),则m= ;
(3)在图中以A,B,C,E为顶点构成平行四边形,则E点的坐标为 .
三、解答题
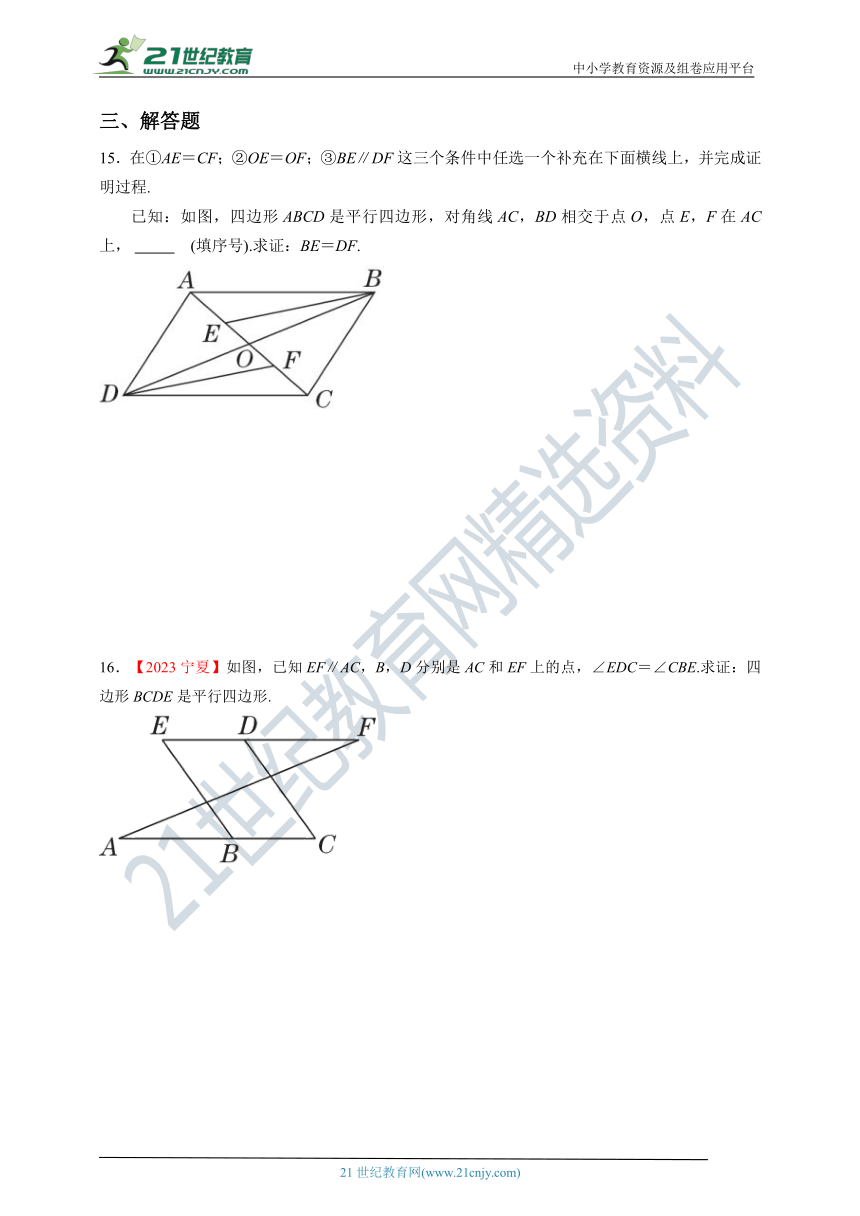
15.在①AE=CF;②OE=OF;③BE∥DF这三个条件中任选一个补充在下面横线上,并完成证明过程.
已知:如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O,点E,F在AC上, (填序号).求证:BE=DF.
16.【2023宁夏】如图,已知EF∥AC,B,D分别是AC和EF上的点,∠EDC=∠CBE.求证:四边形BCDE是平行四边形.
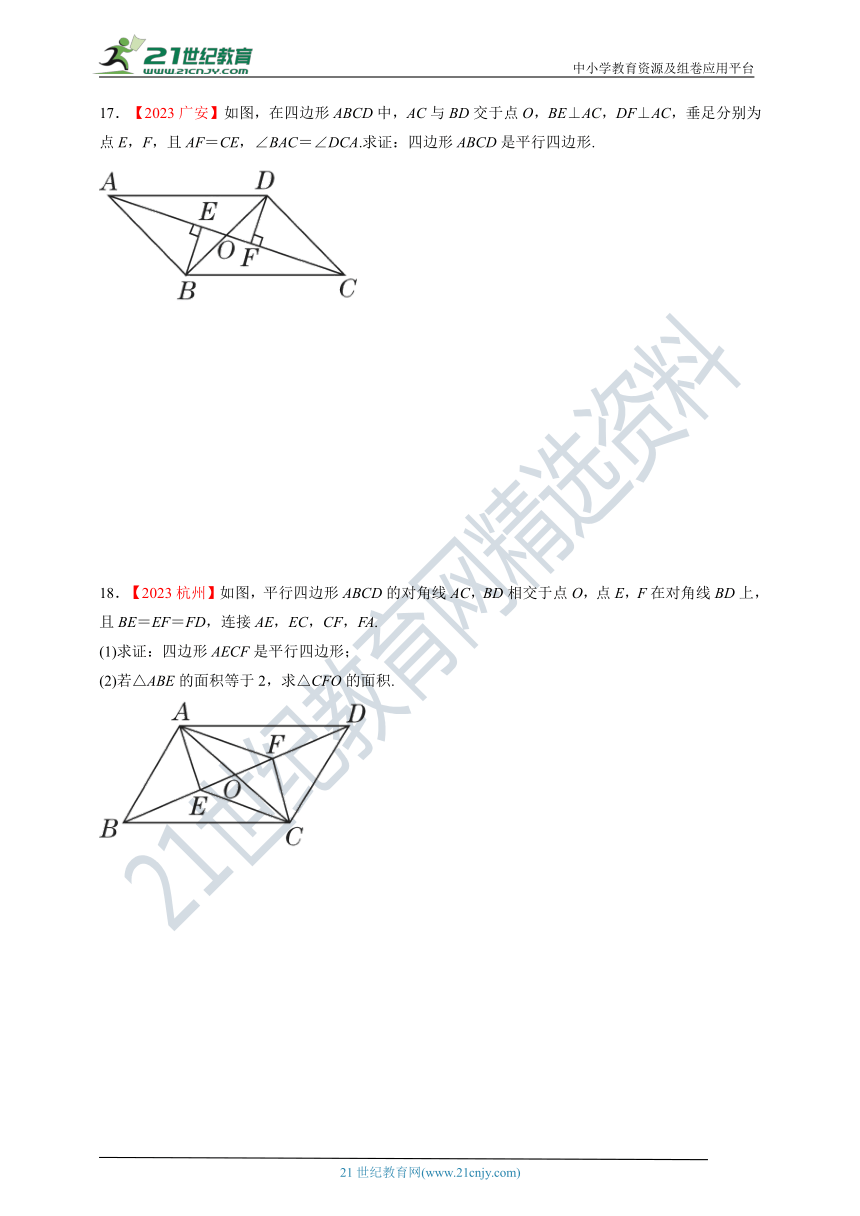
17.【2023广安】如图,在四边形ABCD中,AC与BD交于点O,BE⊥AC,DF⊥AC,垂足分别为点E,F,且AF=CE,∠BAC=∠DCA.求证:四边形ABCD是平行四边形.
18.【2023杭州】如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=EF=FD,连接AE,EC,CF,FA.
(1)求证:四边形AECF是平行四边形;
(2)若△ABE的面积等于2,求△CFO的面积.
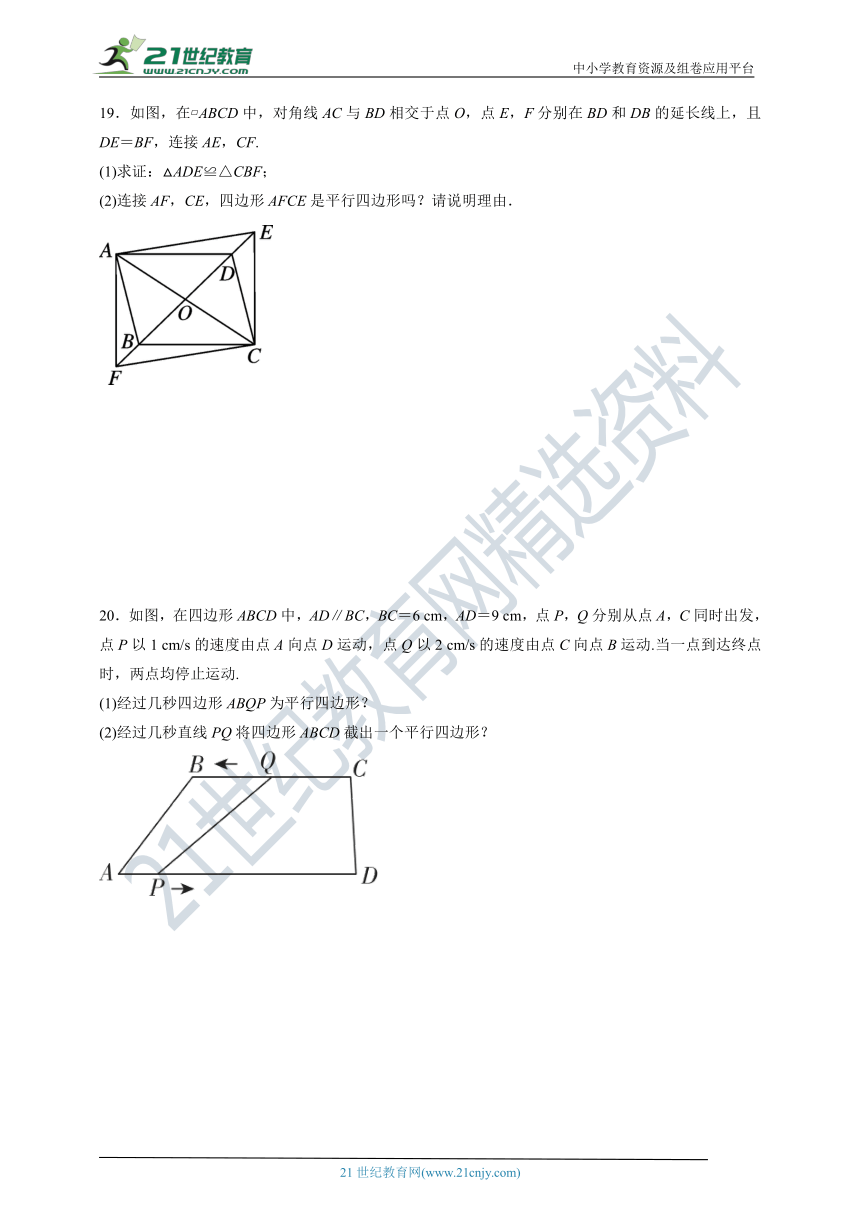
19.如图,在 ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.
(1)求证:△ADE≌△CBF;
(2)连接AF,CE,四边形AFCE是平行四边形吗?请说明理由.
20.如图,在四边形ABCD中,AD∥BC,BC=6 cm,AD=9 cm,点P,Q分别从点A,C同时出发,点P以1 cm/s的速度由点A向点D运动,点Q以2 cm/s的速度由点C向点B运动.当一点到达终点时,两点均停止运动.
(1)经过几秒四边形ABQP为平行四边形?
(2)经过几秒直线PQ将四边形ABCD截出一个平行四边形?
21.如图,在 ABCD中,点E在AD边上,点F在BC边上,且AE=CF,连接AF,BE相交于点M,连接CE,DF相交于点N.
(1)如图①,求证:四边形EMFN为平行四边形;
(2)如图②,连接MN,若E是AD的中点,在不添加任何辅助线的情况下,请直接写出图②中以MN为边的所有平行四边形.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.下面给出了四边形ABCD中∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的是( C )
A.1∶2∶3∶4 B.2∶2∶3∶3 C.2∶3∶2∶3 D.2∶3∶3∶2
2.不能判定四边形ABCD为平行四边形的条件是( C )
A.AB=CD,AD=BC B.AB=CD,AB∥CD
C.AB=CD,AD∥BC D.AD=BC,AD∥BC
3.在四边形ABCD中,AD∥BC,若四边形ABCD是平行四边形,则还需要满足( C )
A.∠A+∠B=180° B.∠A+∠C=180° C.∠B+∠C=180° D.∠B+∠D=180°
4.如图,在四边形ABCD中,AB=CD,BC=AD.若∠B=110°,则∠A的度数为( C )
A.110° B.80° C.70° D.90°
第4题图 第5题图 第6题图
5.如图,四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,添加下列条件后仍无法判定四边形ABCD是平行四边形的是( A )
A.AB=CD B.AB∥CD C.OB=OD D.∠ADB=∠CBD
6.如图,AB=CD=EF,且△ACE≌△BDF,则图中平行四边形的个数为( C )
A.1 B.2 C.3 D.4
7.在四边形ABCD中:①AB∥CD;②AD∥BC;③AB=CD;④AD=BC,从以上选择两个条件使四边形ABCD为平行四边形的选法共有( B )
A.3种 B.4种 C.5种 D.6种
8.在平面直角坐标系中,已知点A(0,0),B(2,2),C(3,0),若以点A,B,C,D为顶点的四边形是平行四边形,则点D的坐标不可能为( D )
A.(-1,2) B.(5,2) C.(1,-2) D.(2,-2)
9.四边形的四边长分别是a,b,c,d,其中a,c是对边,且满足a2+b2+c2+d2=2ac+2bd,则这个四边形是( D )
A.任意四边形 B.四边都相等的四边形
C.对角线互相垂直的四边形 D.平行四边形
10.如图,等边△ABC的边长为6 cm,射线AG∥BC,点E从点A出发沿射线AG以1 cm/s的速度运动,点F从点B出发沿射线BC以2 cm/s的速度运动.设运动时间为t(s),当以A,C,E,F为顶点的四边形是平行四边形时,运动时间t为( D )
A.1 s或2 s B.2 s或3 s C.2 s或4 s D.2 s或6 s
第10题图 第11题图 第12题图
二、填空题
11.在如图的网格中,以格点A,B,C,D,E,F中的4个点为顶点,能画出平行四边形的个数为 .
【答案】3
12.如图,在梯形ABCD中,AD∥BC,∠B=50°,∠C=80°,AE∥CD交BC于点E,若AD=2,BC=5,则边CD的长是 .
【答案】3
13.如图,在 ABCD中,E,F分别是边BC,AD上的点,①AE∥CF;②BE=FD;③∠1=∠2;④AE=CF,若要添加其中一个条件,使四边形AECF一定是平行四边形,则添加的条件可以是 .(填序号)
【答案】①②③
第13题图 第14题图
14.如图,将等边三角形的三条边分别8等分,按顺时针方向(图中箭头方向)标注等分点的序号0,1,2,3,4,5,6,7,8,将不同边上的序号和为8的两点依次连接起来,这样就建立了“三角形”坐标系,在建立的“三角形”坐标系内,每一点的坐标用过这一点且平行(或重合)于原三角形三条边的直线与三边交点的序号来表示(水平方向开始,按顺时针方向),如点A的坐标可表示为(1,2,5),点B的坐标可表示为(3,1,4).
(1)按此方法,则点C的坐标可表示为 ,点D的坐标可表示为 ;
(2)若P点的坐标为(3,m,m-1),则m= ;
(3)在图中以A,B,C,E为顶点构成平行四边形,则E点的坐标为 .
【答案】(1) (3,2,3) (5,3,0)
(2)3
(3) (5,1,2)或(1,1,6)或(1,3,4)
三、解答题
15.在①AE=CF;②OE=OF;③BE∥DF这三个条件中任选一个补充在下面横线上,并完成证明过程.
已知:如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O,点E,F在AC上, (填序号).求证:BE=DF.
②
【证明】如图,连接BF,DE.
∵四边形ABCD是平行四边形,
∴OB=OD.
∵OE=OF,∴四边形BEDF为平行四边形.
∴BE=DF.(答案不唯一)
16.【2023宁夏】如图,已知EF∥AC,B,D分别是AC和EF上的点,∠EDC=∠CBE.求证:四边形BCDE是平行四边形.
【证明】∵EF∥AC,
∴∠EDC+∠C=180°.
又∵∠EDC=∠CBE,
∴∠CBE+∠C=180°.
∴EB∥DC.
∵DE∥BC,BE∥CD,
∴四边形BCDE是平行四边形.
17.【2023广安】如图,在四边形ABCD中,AC与BD交于点O,BE⊥AC,DF⊥AC,垂足分别为点E,F,且AF=CE,∠BAC=∠DCA.求证:四边形ABCD是平行四边形.
【证明】∵AF=CE,
∴AF-EF=CE-EF.∴AE=CF.
∵∠BAC=∠DCA,∴AB∥CD.
∵BE⊥AC,DF⊥AC,∴∠AEB=∠CFD=90°.
在△ABE和△CDF中,
∴△ABE≌△CDF(ASA).∴AB=CD.
∴四边形ABCD是平行四边形.
18.【2023杭州】如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=EF=FD,连接AE,EC,CF,FA.
(1)求证:四边形AECF是平行四边形;
(2)若△ABE的面积等于2,求△CFO的面积.
(1)【证明】∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO.
∵BE=DF,∴EO=FO.
∴四边形AECF是平行四边形.
(2)【解】∵BE=EF,∴S△ABE=S△AEF=2.
∵四边形AECF是平行四边形,
∴S△AEF=S△CEF=2.
∵EO=FO,∴△CFO的面积为1.
19.如图,在 ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.
(1)求证:△ADE≌△CBF;
(2)连接AF,CE,四边形AFCE是平行四边形吗?请说明理由.
解:(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
∴△ADE≌△CBF(SAS).
(2)四边形AFCE是平行四边形.理由如下:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵DE=BF,
∴OD+DE=OB+BF,
即OE=OF,
∴四边形AFCE是平行四边形.
20.如图,在四边形ABCD中,AD∥BC,BC=6 cm,AD=9 cm,点P,Q分别从点A,C同时出发,点P以1 cm/s的速度由点A向点D运动,点Q以2 cm/s的速度由点C向点B运动.当一点到达终点时,两点均停止运动.
(1)经过几秒四边形ABQP为平行四边形?
(2)经过几秒直线PQ将四边形ABCD截出一个平行四边形?
【解】(1)设经过t s四边形ABQP为平行四边形.
根据题意,得AP=t cm,CQ=2t cm,则BQ=(6-2t)cm.
∵AD∥BC,
∴当AP=BQ时,四边形ABQP是平行四边形,
∴t=6-2t,解得t=2.
即经过2 s四边形ABQP为平行四边形.
【解】(2)由(1)知,经过2 s四边形ABQP是平行四边形,设经过x s直线PQ将四边形ABCD截出另一个平行四边形DCQP.根据题意,得AP=x cm,CQ=2x cm,
则PD=(9-x)cm.∵AD∥BC,
∴当CQ=PD时,四边形DCQP是平行四边形,
∴2x=9-x,解得x=3.
综上,经过2 s或3 s直线PQ将四边形ABCD截出一个平行四边形.
21.如图,在 ABCD中,点E在AD边上,点F在BC边上,且AE=CF,连接AF,BE相交于点M,连接CE,DF相交于点N.
(1)如图①,求证:四边形EMFN为平行四边形;
(2)如图②,连接MN,若E是AD的中点,在不添加任何辅助线的情况下,请直接写出图②中以MN为边的所有平行四边形.
解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,∴DE=BF,
∴四边形AECF和四边形DEBF都是平行四边形,
∴AF∥CE,BE∥DF,
∴四边形EMFN是平行四边形.
(2)以MN为边的所有平行四边形为:平行四边形BMNF、平行四边形EMND、平行四边形AMNE、
平行四边形FMNC.理由如下:
连接EF,如图所示,
∵E是AD的中点,∴AE=DE,
同(1)得四边形ABFE、四边形CDEF、四边形AECF和四边形DEBF都是平行四边形,
∴AM=FM=AF,BM=EM=BE,EN=CN=CE,FN=DN=DF,AF∥CE,AF=CE,BE∥DF,BE=DF,
∴AM=EN=FM=CN,BM=FN=DN=EM,
∴四边形AMNE、四边形FMNC、四边形BMNF、四边形EMND是平行四边形.
18.1.2 平行四边形的判定
第1课时 平行四边形的判定
一、选择题
1.下面给出了四边形ABCD中∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的是( )
A.1∶2∶3∶4 B.2∶2∶3∶3 C.2∶3∶2∶3 D.2∶3∶3∶2
2.不能判定四边形ABCD为平行四边形的条件是( )
A.AB=CD,AD=BC B.AB=CD,AB∥CD
C.AB=CD,AD∥BC D.AD=BC,AD∥BC
3.在四边形ABCD中,AD∥BC,若四边形ABCD是平行四边形,则还需要满足( )
A.∠A+∠B=180° B.∠A+∠C=180° C.∠B+∠C=180° D.∠B+∠D=180°
4.如图,在四边形ABCD中,AB=CD,BC=AD.若∠B=110°,则∠A的度数为( )
A.110° B.80° C.70° D.90°
第4题图 第5题图 第6题图
5.如图,四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,添加下列条件后仍无法判定四边形ABCD是平行四边形的是( )
A.AB=CD B.AB∥CD C.OB=OD D.∠ADB=∠CBD
6.如图,AB=CD=EF,且△ACE≌△BDF,则图中平行四边形的个数为( )
A.1 B.2 C.3 D.4
7.在四边形ABCD中:①AB∥CD;②AD∥BC;③AB=CD;④AD=BC,从以上选择两个条件使四边形ABCD为平行四边形的选法共有( )
A.3种 B.4种 C.5种 D.6种
8.在平面直角坐标系中,已知点A(0,0),B(2,2),C(3,0),若以点A,B,C,D为顶点的四边形是平行四边形,则点D的坐标不可能为( )
A.(-1,2) B.(5,2) C.(1,-2) D.(2,-2)
9.四边形的四边长分别是a,b,c,d,其中a,c是对边,且满足a2+b2+c2+d2=2ac+2bd,则这个四边形是( )
A.任意四边形 B.四边都相等的四边形
C.对角线互相垂直的四边形 D.平行四边形
10.如图,等边△ABC的边长为6 cm,射线AG∥BC,点E从点A出发沿射线AG以1 cm/s的速度运动,点F从点B出发沿射线BC以2 cm/s的速度运动.设运动时间为t(s),当以A,C,E,F为顶点的四边形是平行四边形时,运动时间t为( )
A.1 s或2 s B.2 s或3 s C.2 s或4 s D.2 s或6 s
第10题图 第11题图 第12题图
二、填空题
11.在如图的网格中,以格点A,B,C,D,E,F中的4个点为顶点,能画出平行四边形的个数为 .
12.如图,在梯形ABCD中,AD∥BC,∠B=50°,∠C=80°,AE∥CD交BC于点E,若AD=2,BC=5,则边CD的长是 .
13.如图,在 ABCD中,E,F分别是边BC,AD上的点,①AE∥CF;②BE=FD;③∠1=∠2;④AE=CF,若要添加其中一个条件,使四边形AECF一定是平行四边形,则添加的条件可以是 .(填序号)
第13题图 第14题图
14.如图,将等边三角形的三条边分别8等分,按顺时针方向(图中箭头方向)标注等分点的序号0,1,2,3,4,5,6,7,8,将不同边上的序号和为8的两点依次连接起来,这样就建立了“三角形”坐标系,在建立的“三角形”坐标系内,每一点的坐标用过这一点且平行(或重合)于原三角形三条边的直线与三边交点的序号来表示(水平方向开始,按顺时针方向),如点A的坐标可表示为(1,2,5),点B的坐标可表示为(3,1,4).
(1)按此方法,则点C的坐标可表示为 ,点D的坐标可表示为 ;
(2)若P点的坐标为(3,m,m-1),则m= ;
(3)在图中以A,B,C,E为顶点构成平行四边形,则E点的坐标为 .
三、解答题
15.在①AE=CF;②OE=OF;③BE∥DF这三个条件中任选一个补充在下面横线上,并完成证明过程.
已知:如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O,点E,F在AC上, (填序号).求证:BE=DF.
16.【2023宁夏】如图,已知EF∥AC,B,D分别是AC和EF上的点,∠EDC=∠CBE.求证:四边形BCDE是平行四边形.
17.【2023广安】如图,在四边形ABCD中,AC与BD交于点O,BE⊥AC,DF⊥AC,垂足分别为点E,F,且AF=CE,∠BAC=∠DCA.求证:四边形ABCD是平行四边形.
18.【2023杭州】如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=EF=FD,连接AE,EC,CF,FA.
(1)求证:四边形AECF是平行四边形;
(2)若△ABE的面积等于2,求△CFO的面积.
19.如图,在 ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.
(1)求证:△ADE≌△CBF;
(2)连接AF,CE,四边形AFCE是平行四边形吗?请说明理由.
20.如图,在四边形ABCD中,AD∥BC,BC=6 cm,AD=9 cm,点P,Q分别从点A,C同时出发,点P以1 cm/s的速度由点A向点D运动,点Q以2 cm/s的速度由点C向点B运动.当一点到达终点时,两点均停止运动.
(1)经过几秒四边形ABQP为平行四边形?
(2)经过几秒直线PQ将四边形ABCD截出一个平行四边形?
21.如图,在 ABCD中,点E在AD边上,点F在BC边上,且AE=CF,连接AF,BE相交于点M,连接CE,DF相交于点N.
(1)如图①,求证:四边形EMFN为平行四边形;
(2)如图②,连接MN,若E是AD的中点,在不添加任何辅助线的情况下,请直接写出图②中以MN为边的所有平行四边形.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.下面给出了四边形ABCD中∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的是( C )
A.1∶2∶3∶4 B.2∶2∶3∶3 C.2∶3∶2∶3 D.2∶3∶3∶2
2.不能判定四边形ABCD为平行四边形的条件是( C )
A.AB=CD,AD=BC B.AB=CD,AB∥CD
C.AB=CD,AD∥BC D.AD=BC,AD∥BC
3.在四边形ABCD中,AD∥BC,若四边形ABCD是平行四边形,则还需要满足( C )
A.∠A+∠B=180° B.∠A+∠C=180° C.∠B+∠C=180° D.∠B+∠D=180°
4.如图,在四边形ABCD中,AB=CD,BC=AD.若∠B=110°,则∠A的度数为( C )
A.110° B.80° C.70° D.90°
第4题图 第5题图 第6题图
5.如图,四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,添加下列条件后仍无法判定四边形ABCD是平行四边形的是( A )
A.AB=CD B.AB∥CD C.OB=OD D.∠ADB=∠CBD
6.如图,AB=CD=EF,且△ACE≌△BDF,则图中平行四边形的个数为( C )
A.1 B.2 C.3 D.4
7.在四边形ABCD中:①AB∥CD;②AD∥BC;③AB=CD;④AD=BC,从以上选择两个条件使四边形ABCD为平行四边形的选法共有( B )
A.3种 B.4种 C.5种 D.6种
8.在平面直角坐标系中,已知点A(0,0),B(2,2),C(3,0),若以点A,B,C,D为顶点的四边形是平行四边形,则点D的坐标不可能为( D )
A.(-1,2) B.(5,2) C.(1,-2) D.(2,-2)
9.四边形的四边长分别是a,b,c,d,其中a,c是对边,且满足a2+b2+c2+d2=2ac+2bd,则这个四边形是( D )
A.任意四边形 B.四边都相等的四边形
C.对角线互相垂直的四边形 D.平行四边形
10.如图,等边△ABC的边长为6 cm,射线AG∥BC,点E从点A出发沿射线AG以1 cm/s的速度运动,点F从点B出发沿射线BC以2 cm/s的速度运动.设运动时间为t(s),当以A,C,E,F为顶点的四边形是平行四边形时,运动时间t为( D )
A.1 s或2 s B.2 s或3 s C.2 s或4 s D.2 s或6 s
第10题图 第11题图 第12题图
二、填空题
11.在如图的网格中,以格点A,B,C,D,E,F中的4个点为顶点,能画出平行四边形的个数为 .
【答案】3
12.如图,在梯形ABCD中,AD∥BC,∠B=50°,∠C=80°,AE∥CD交BC于点E,若AD=2,BC=5,则边CD的长是 .
【答案】3
13.如图,在 ABCD中,E,F分别是边BC,AD上的点,①AE∥CF;②BE=FD;③∠1=∠2;④AE=CF,若要添加其中一个条件,使四边形AECF一定是平行四边形,则添加的条件可以是 .(填序号)
【答案】①②③
第13题图 第14题图
14.如图,将等边三角形的三条边分别8等分,按顺时针方向(图中箭头方向)标注等分点的序号0,1,2,3,4,5,6,7,8,将不同边上的序号和为8的两点依次连接起来,这样就建立了“三角形”坐标系,在建立的“三角形”坐标系内,每一点的坐标用过这一点且平行(或重合)于原三角形三条边的直线与三边交点的序号来表示(水平方向开始,按顺时针方向),如点A的坐标可表示为(1,2,5),点B的坐标可表示为(3,1,4).
(1)按此方法,则点C的坐标可表示为 ,点D的坐标可表示为 ;
(2)若P点的坐标为(3,m,m-1),则m= ;
(3)在图中以A,B,C,E为顶点构成平行四边形,则E点的坐标为 .
【答案】(1) (3,2,3) (5,3,0)
(2)3
(3) (5,1,2)或(1,1,6)或(1,3,4)
三、解答题
15.在①AE=CF;②OE=OF;③BE∥DF这三个条件中任选一个补充在下面横线上,并完成证明过程.
已知:如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O,点E,F在AC上, (填序号).求证:BE=DF.
②
【证明】如图,连接BF,DE.
∵四边形ABCD是平行四边形,
∴OB=OD.
∵OE=OF,∴四边形BEDF为平行四边形.
∴BE=DF.(答案不唯一)
16.【2023宁夏】如图,已知EF∥AC,B,D分别是AC和EF上的点,∠EDC=∠CBE.求证:四边形BCDE是平行四边形.
【证明】∵EF∥AC,
∴∠EDC+∠C=180°.
又∵∠EDC=∠CBE,
∴∠CBE+∠C=180°.
∴EB∥DC.
∵DE∥BC,BE∥CD,
∴四边形BCDE是平行四边形.
17.【2023广安】如图,在四边形ABCD中,AC与BD交于点O,BE⊥AC,DF⊥AC,垂足分别为点E,F,且AF=CE,∠BAC=∠DCA.求证:四边形ABCD是平行四边形.
【证明】∵AF=CE,
∴AF-EF=CE-EF.∴AE=CF.
∵∠BAC=∠DCA,∴AB∥CD.
∵BE⊥AC,DF⊥AC,∴∠AEB=∠CFD=90°.
在△ABE和△CDF中,
∴△ABE≌△CDF(ASA).∴AB=CD.
∴四边形ABCD是平行四边形.
18.【2023杭州】如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=EF=FD,连接AE,EC,CF,FA.
(1)求证:四边形AECF是平行四边形;
(2)若△ABE的面积等于2,求△CFO的面积.
(1)【证明】∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO.
∵BE=DF,∴EO=FO.
∴四边形AECF是平行四边形.
(2)【解】∵BE=EF,∴S△ABE=S△AEF=2.
∵四边形AECF是平行四边形,
∴S△AEF=S△CEF=2.
∵EO=FO,∴△CFO的面积为1.
19.如图,在 ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.
(1)求证:△ADE≌△CBF;
(2)连接AF,CE,四边形AFCE是平行四边形吗?请说明理由.
解:(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
∴△ADE≌△CBF(SAS).
(2)四边形AFCE是平行四边形.理由如下:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵DE=BF,
∴OD+DE=OB+BF,
即OE=OF,
∴四边形AFCE是平行四边形.
20.如图,在四边形ABCD中,AD∥BC,BC=6 cm,AD=9 cm,点P,Q分别从点A,C同时出发,点P以1 cm/s的速度由点A向点D运动,点Q以2 cm/s的速度由点C向点B运动.当一点到达终点时,两点均停止运动.
(1)经过几秒四边形ABQP为平行四边形?
(2)经过几秒直线PQ将四边形ABCD截出一个平行四边形?
【解】(1)设经过t s四边形ABQP为平行四边形.
根据题意,得AP=t cm,CQ=2t cm,则BQ=(6-2t)cm.
∵AD∥BC,
∴当AP=BQ时,四边形ABQP是平行四边形,
∴t=6-2t,解得t=2.
即经过2 s四边形ABQP为平行四边形.
【解】(2)由(1)知,经过2 s四边形ABQP是平行四边形,设经过x s直线PQ将四边形ABCD截出另一个平行四边形DCQP.根据题意,得AP=x cm,CQ=2x cm,
则PD=(9-x)cm.∵AD∥BC,
∴当CQ=PD时,四边形DCQP是平行四边形,
∴2x=9-x,解得x=3.
综上,经过2 s或3 s直线PQ将四边形ABCD截出一个平行四边形.
21.如图,在 ABCD中,点E在AD边上,点F在BC边上,且AE=CF,连接AF,BE相交于点M,连接CE,DF相交于点N.
(1)如图①,求证:四边形EMFN为平行四边形;
(2)如图②,连接MN,若E是AD的中点,在不添加任何辅助线的情况下,请直接写出图②中以MN为边的所有平行四边形.
解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,∴DE=BF,
∴四边形AECF和四边形DEBF都是平行四边形,
∴AF∥CE,BE∥DF,
∴四边形EMFN是平行四边形.
(2)以MN为边的所有平行四边形为:平行四边形BMNF、平行四边形EMND、平行四边形AMNE、
平行四边形FMNC.理由如下:
连接EF,如图所示,
∵E是AD的中点,∴AE=DE,
同(1)得四边形ABFE、四边形CDEF、四边形AECF和四边形DEBF都是平行四边形,
∴AM=FM=AF,BM=EM=BE,EN=CN=CE,FN=DN=DF,AF∥CE,AF=CE,BE∥DF,BE=DF,
∴AM=EN=FM=CN,BM=FN=DN=EM,
∴四边形AMNE、四边形FMNC、四边形BMNF、四边形EMND是平行四边形.
