18.1.2.2 三角形的中位线同步练习(含答案)
文档属性
| 名称 | 18.1.2.2 三角形的中位线同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-04 00:00:00 | ||
图片预览



文档简介
18.1 平行四边形
18.1.2 平行四边形的判定
第2课时 三角形的中位线
一、选择题
1.【2023云南】如图,A,B两点被池塘隔开,A,B,C三点不共线.设AC,BC的中点分别为M,N.若MN=3m,则AB=( )
A.4 m B.6 m C.8 m D.10 m
第1题图 第2题图 第3题图
2.如图,为了测量位于一水塘旁的两点A,B间的距离,在地面上确定点O,分别取OA,OB的中点C,D,量得CD=20 m,则A,B之间的距离是( )
A.10 m B.20 m C.40 m D.80 m
3.如图,在△ABC中,AB=4,AC=5,BC=6,D,E,F分别是AB,BC,CA的中点,连接DE,EF,则四边形ADEF的周长为( )
A.6 B.9 C.12 D.15
4.如图,在△ABC中,D,E分别是AC,AB的中点,点F是BC的延长线上一点,∠A=35°,∠AED=30°,则∠ACF的度数为( )
A.60° B.65° C.70° D.85°
第4题图 第5题图 第6题图
5.如图,在△ABC中,点D,E分别是AB,BC的中点,点F在DE的延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件可以是( )
A.∠B=∠F B.∠B=∠BCF C.AC=CF D.AD=CF
6.如图,在Rt△ABC中,点D,E,F分别是边AB,AC,BC的中点,AC=8,BC=6,则四边形CEDF的面积是( )
A.6 B.12 C.24 D.48
7.如图,以△ABC的三个顶点及三边中点为顶点的平行四边形共有( )
A.1个 B.2个 C.3个 D.4个
第7题图 第8题图 第9题图
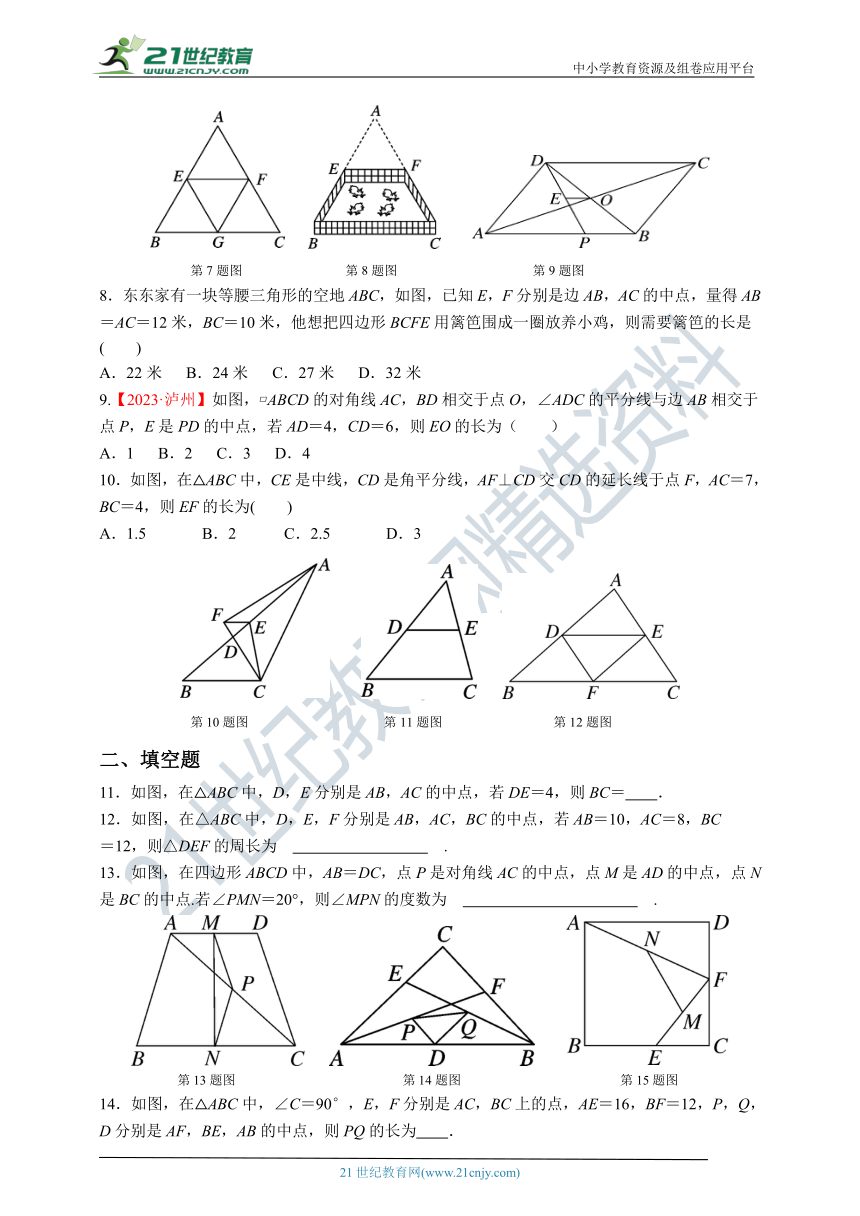
8.东东家有一块等腰三角形的空地ABC,如图,已知E,F分别是边AB,AC的中点,量得AB=AC=12米,BC=10米,他想把四边形BCFE用篱笆围成一圈放养小鸡,则需要篱笆的长是( )
A.22米 B.24米 C.27米 D.32米
9.【2023·泸州】如图, ABCD的对角线AC,BD相交于点O,∠ADC的平分线与边AB相交于点P,E是PD的中点,若AD=4,CD=6,则EO的长为( )
A.1 B.2 C.3 D.4
10.如图,在△ABC中,CE是中线,CD是角平分线,AF⊥CD交CD的延长线于点F,AC=7,BC=4,则EF的长为( )
A.1.5 B.2 C.2.5 D.3
第10题图 第11题图 第12题图
二、填空题
11.如图,在△ABC中,D,E分别是AB,AC的中点,若DE=4,则BC= .
12.如图,在△ABC中,D,E,F分别是AB,AC,BC的中点,若AB=10,AC=8,BC
=12,则△DEF的周长为 .
13.如图,在四边形ABCD中,AB=DC,点P是对角线AC的中点,点M是AD的中点,点N是BC的中点.若∠PMN=20°,则∠MPN的度数为 .
第13题图 第14题图 第15题图
14.如图,在△ABC中,∠C=90°,E,F分别是AC,BC上的点,AE=16,BF=12,P,Q,D分别是AF,BE,AB的中点,则PQ的长为 .
15.【202广西】如图,在边长为2的正方形ABCD中,E,F分别是BC,CD上的动点,M,N分别是EF,AF的中点,则MN的最大值为 .
三、解答题
16.如图,在Rt△ABC中,∠C=90°,∠B=60°,AB=8 cm,E,F分别为边AC,AB的中点.
(1)求∠A的度数;
(2)求EF的长.
17.如图,在△ABC中,D,E,F分别为边AB,BC,CA的中点.求证:四边形DECF是平行四边形.
18.如图,在△ABC中,D,E分别是AC,AB的中点,点F是CB延长线上的一点,且CF=3BF,连接DB,EF.
(1)求证:四边形DEFB是平行四边形;
(2)若∠ACB=90°,AC=12 cm,DE=4 cm,求四边形DEFB的周长.
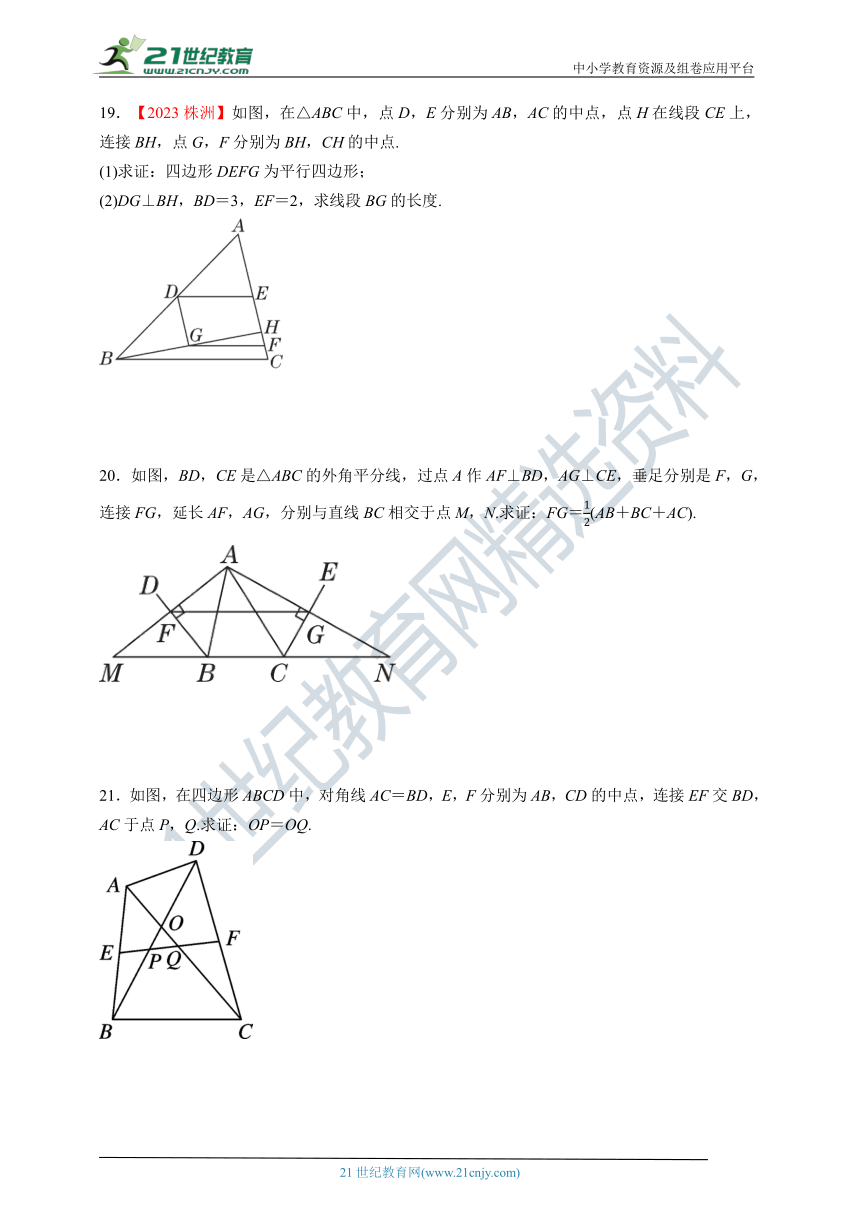
19.【2023株洲】如图,在△ABC中,点D,E分别为AB,AC的中点,点H在线段CE上,连接BH,点G,F分别为BH,CH的中点.
(1)求证:四边形DEFG为平行四边形;
(2)DG⊥BH,BD=3,EF=2,求线段BG的长度.
20.如图,BD,CE是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别是F,G,连接FG,延长AF,AG,分别与直线BC相交于点M,N.求证:FG=(AB+BC+AC).
21.如图,在四边形ABCD中,对角线AC=BD,E,F分别为AB,CD的中点,连接EF交BD,AC于点P,Q.求证:OP=OQ.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.【2023云南】如图,A,B两点被池塘隔开,A,B,C三点不共线.设AC,BC的中点分别为M,N.若MN=3m,则AB=( B )
A.4 m B.6 m C.8 m D.10 m
第1题图 第2题图 第3题图
2.如图,为了测量位于一水塘旁的两点A,B间的距离,在地面上确定点O,分别取OA,OB的中点C,D,量得CD=20 m,则A,B之间的距离是( C )
A.10 m B.20 m C.40 m D.80 m
3.如图,在△ABC中,AB=4,AC=5,BC=6,D,E,F分别是AB,BC,CA的中点,连接DE,EF,则四边形ADEF的周长为( B )
A.6 B.9 C.12 D.15
4.如图,在△ABC中,D,E分别是AC,AB的中点,点F是BC的延长线上一点,∠A=35°,∠AED=30°,则∠ACF的度数为( B )
A.60° B.65° C.70° D.85°
第4题图 第5题图 第6题图
5.如图,在△ABC中,点D,E分别是AB,BC的中点,点F在DE的延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件可以是( B )
A.∠B=∠F B.∠B=∠BCF C.AC=CF D.AD=CF
6.如图,在Rt△ABC中,点D,E,F分别是边AB,AC,BC的中点,AC=8,BC=6,则四边形CEDF的面积是( B )
A.6 B.12 C.24 D.48
7.如图,以△ABC的三个顶点及三边中点为顶点的平行四边形共有( C )
A.1个 B.2个 C.3个 D.4个
第7题图 第8题图 第9题图
8.东东家有一块等腰三角形的空地ABC,如图,已知E,F分别是边AB,AC的中点,量得AB=AC=12米,BC=10米,他想把四边形BCFE用篱笆围成一圈放养小鸡,则需要篱笆的长是( C )
A.22米 B.24米 C.27米 D.32米
9.【2023·泸州】如图, ABCD的对角线AC,BD相交于点O,∠ADC的平分线与边AB相交于点P,E是PD的中点,若AD=4,CD=6,则EO的长为( A )
A.1 B.2 C.3 D.4
10.如图,在△ABC中,CE是中线,CD是角平分线,AF⊥CD交CD的延长线于点F,AC=7,BC=4,则EF的长为( A )
A.1.5 B.2 C.2.5 D.3
【解析】延长AF,CB交于点G,
∵CD是△ABC的角平分线,∴∠ACF=∠BCF,在△ACF和△GCF中,
∴△ACF≌△GCF(ASA),∴CG=AC=7,AF=FG,∴BG=CG-CB=3,∵AE=EB,AF=FG,∴EF=BG=1.5.
第10题图 第11题图 第12题图
二、填空题
11.如图,在△ABC中,D,E分别是AB,AC的中点,若DE=4,则BC= .
【答案】8
12.如图,在△ABC中,D,E,F分别是AB,AC,BC的中点,若AB=10,AC=8,BC
=12,则△DEF的周长为 .
【答案】15
13.如图,在四边形ABCD中,AB=DC,点P是对角线AC的中点,点M是AD的中点,点N是BC的中点.若∠PMN=20°,则∠MPN的度数为 .
【答案】150°
第13题图 第14题图 第15题图
14.如图,在△ABC中,∠C=90°,E,F分别是AC,BC上的点,AE=16,BF=12,P,Q,D分别是AF,BE,AB的中点,则PQ的长为 .
【答案】10
15.【202广西】如图,在边长为2的正方形ABCD中,E,F分别是BC,CD上的动点,M,N分别是EF,AF的中点,则MN的最大值为 .
【答案】
三、解答题
16.如图,在Rt△ABC中,∠C=90°,∠B=60°,AB=8 cm,E,F分别为边AC,AB的中点.
(1)求∠A的度数;
(2)求EF的长.
解:(1)∠A=30°.
(2)EF=2 cm.
17.如图,在△ABC中,D,E,F分别为边AB,BC,CA的中点.求证:四边形DECF是平行四边形.
证明:∵D,E,F分别为边AB,BC,CA的中点,
∴DF,DE为△ABC的中位线.
∴DF∥BC,DE∥AC,
∴四边形DECF是平行四边形.
18.如图,在△ABC中,D,E分别是AC,AB的中点,点F是CB延长线上的一点,且CF=3BF,连接DB,EF.
(1)求证:四边形DEFB是平行四边形;
(2)若∠ACB=90°,AC=12 cm,DE=4 cm,求四边形DEFB的周长.
解:(1)证明:∵D,E分别是AC,AB的中点,
∴DE是△ABC的中位线,
∴DE∥BC,BC=2DE,
∵CF=3BF,
∴BC=2BF,
∴DE=BF,
又DE∥BF,
∴四边形DEFB是平行四边形.
(2)由(1)得BC=2DE=8(cm),BF=DE=4 cm,四边形DEFB是平行四边形,∴BD=EF,
∵D是AC的中点,AC=12 cm,∴CD=AC=6(cm),
∵∠ACB=90°,
∴BD===10(cm),
∴平行四边形DEFB的周长为2(DE+BD)=2×(4+10)=28(cm).
19.【2023株洲】如图,在△ABC中,点D,E分别为AB,AC的中点,点H在线段CE上,连接BH,点G,F分别为BH,CH的中点.
(1)求证:四边形DEFG为平行四边形;
(2)DG⊥BH,BD=3,EF=2,求线段BG的长度.
(1)【证明】∵点D,E分别为AB,AC的中点,点G,F分别为BH,CH的中点,
∴DE是△ABC的中位线,GF是△HBC的中位线.
∴DE∥BC,DE=BC,GF∥BC,GF=BC.
∴DE∥GF,DE=GF.
∴四边形DEFG为平行四边形.
(2)【解】∵四边形DEFG为平行四边形,
∴DG=EF=2.∵DG⊥BH,∴∠DGB=90°.
∴BG===,
即线段BG的长度为.
20.如图,BD,CE是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别是F,G,连接FG,延长AF,AG,分别与直线BC相交于点M,N.求证:FG=(AB+BC+AC).
【证明】∵BD是∠MBA的平分线,
∴∠ABF=∠MBF.
∵AF⊥BD,∴∠MFB=∠AFB=90°.
∴∠BAF=∠BMF.∴MB=AB.∴AF=MF.
同理可得CN=AC,AG=NG,
∴FG是△AMN的中位线.
∴FG=MN=(MB+BC+CN)=(AB+BC+AC).
21.如图,在四边形ABCD中,对角线AC=BD,E,F分别为AB,CD的中点,连接EF交BD,AC于点P,Q.求证:OP=OQ.
证明:如图,取BC的中点G,连接EG,FG.
∵E,G分别为AB,BC的中点,
∴EG=AC,EG∥AC,
∴∠FEG=∠OQP.
同理,可得FG=BD,FG∥BD,
∴∠EFG=∠OPQ.
∵AC=BD,∴EG=FG,
∴∠FEG=∠EFG,
∴∠OQP=∠OPQ,∴OP=OQ.
18.1.2 平行四边形的判定
第2课时 三角形的中位线
一、选择题
1.【2023云南】如图,A,B两点被池塘隔开,A,B,C三点不共线.设AC,BC的中点分别为M,N.若MN=3m,则AB=( )
A.4 m B.6 m C.8 m D.10 m
第1题图 第2题图 第3题图
2.如图,为了测量位于一水塘旁的两点A,B间的距离,在地面上确定点O,分别取OA,OB的中点C,D,量得CD=20 m,则A,B之间的距离是( )
A.10 m B.20 m C.40 m D.80 m
3.如图,在△ABC中,AB=4,AC=5,BC=6,D,E,F分别是AB,BC,CA的中点,连接DE,EF,则四边形ADEF的周长为( )
A.6 B.9 C.12 D.15
4.如图,在△ABC中,D,E分别是AC,AB的中点,点F是BC的延长线上一点,∠A=35°,∠AED=30°,则∠ACF的度数为( )
A.60° B.65° C.70° D.85°
第4题图 第5题图 第6题图
5.如图,在△ABC中,点D,E分别是AB,BC的中点,点F在DE的延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件可以是( )
A.∠B=∠F B.∠B=∠BCF C.AC=CF D.AD=CF
6.如图,在Rt△ABC中,点D,E,F分别是边AB,AC,BC的中点,AC=8,BC=6,则四边形CEDF的面积是( )
A.6 B.12 C.24 D.48
7.如图,以△ABC的三个顶点及三边中点为顶点的平行四边形共有( )
A.1个 B.2个 C.3个 D.4个
第7题图 第8题图 第9题图
8.东东家有一块等腰三角形的空地ABC,如图,已知E,F分别是边AB,AC的中点,量得AB=AC=12米,BC=10米,他想把四边形BCFE用篱笆围成一圈放养小鸡,则需要篱笆的长是( )
A.22米 B.24米 C.27米 D.32米
9.【2023·泸州】如图, ABCD的对角线AC,BD相交于点O,∠ADC的平分线与边AB相交于点P,E是PD的中点,若AD=4,CD=6,则EO的长为( )
A.1 B.2 C.3 D.4
10.如图,在△ABC中,CE是中线,CD是角平分线,AF⊥CD交CD的延长线于点F,AC=7,BC=4,则EF的长为( )
A.1.5 B.2 C.2.5 D.3
第10题图 第11题图 第12题图
二、填空题
11.如图,在△ABC中,D,E分别是AB,AC的中点,若DE=4,则BC= .
12.如图,在△ABC中,D,E,F分别是AB,AC,BC的中点,若AB=10,AC=8,BC
=12,则△DEF的周长为 .
13.如图,在四边形ABCD中,AB=DC,点P是对角线AC的中点,点M是AD的中点,点N是BC的中点.若∠PMN=20°,则∠MPN的度数为 .
第13题图 第14题图 第15题图
14.如图,在△ABC中,∠C=90°,E,F分别是AC,BC上的点,AE=16,BF=12,P,Q,D分别是AF,BE,AB的中点,则PQ的长为 .
15.【202广西】如图,在边长为2的正方形ABCD中,E,F分别是BC,CD上的动点,M,N分别是EF,AF的中点,则MN的最大值为 .
三、解答题
16.如图,在Rt△ABC中,∠C=90°,∠B=60°,AB=8 cm,E,F分别为边AC,AB的中点.
(1)求∠A的度数;
(2)求EF的长.
17.如图,在△ABC中,D,E,F分别为边AB,BC,CA的中点.求证:四边形DECF是平行四边形.
18.如图,在△ABC中,D,E分别是AC,AB的中点,点F是CB延长线上的一点,且CF=3BF,连接DB,EF.
(1)求证:四边形DEFB是平行四边形;
(2)若∠ACB=90°,AC=12 cm,DE=4 cm,求四边形DEFB的周长.
19.【2023株洲】如图,在△ABC中,点D,E分别为AB,AC的中点,点H在线段CE上,连接BH,点G,F分别为BH,CH的中点.
(1)求证:四边形DEFG为平行四边形;
(2)DG⊥BH,BD=3,EF=2,求线段BG的长度.
20.如图,BD,CE是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别是F,G,连接FG,延长AF,AG,分别与直线BC相交于点M,N.求证:FG=(AB+BC+AC).
21.如图,在四边形ABCD中,对角线AC=BD,E,F分别为AB,CD的中点,连接EF交BD,AC于点P,Q.求证:OP=OQ.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.【2023云南】如图,A,B两点被池塘隔开,A,B,C三点不共线.设AC,BC的中点分别为M,N.若MN=3m,则AB=( B )
A.4 m B.6 m C.8 m D.10 m
第1题图 第2题图 第3题图
2.如图,为了测量位于一水塘旁的两点A,B间的距离,在地面上确定点O,分别取OA,OB的中点C,D,量得CD=20 m,则A,B之间的距离是( C )
A.10 m B.20 m C.40 m D.80 m
3.如图,在△ABC中,AB=4,AC=5,BC=6,D,E,F分别是AB,BC,CA的中点,连接DE,EF,则四边形ADEF的周长为( B )
A.6 B.9 C.12 D.15
4.如图,在△ABC中,D,E分别是AC,AB的中点,点F是BC的延长线上一点,∠A=35°,∠AED=30°,则∠ACF的度数为( B )
A.60° B.65° C.70° D.85°
第4题图 第5题图 第6题图
5.如图,在△ABC中,点D,E分别是AB,BC的中点,点F在DE的延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件可以是( B )
A.∠B=∠F B.∠B=∠BCF C.AC=CF D.AD=CF
6.如图,在Rt△ABC中,点D,E,F分别是边AB,AC,BC的中点,AC=8,BC=6,则四边形CEDF的面积是( B )
A.6 B.12 C.24 D.48
7.如图,以△ABC的三个顶点及三边中点为顶点的平行四边形共有( C )
A.1个 B.2个 C.3个 D.4个
第7题图 第8题图 第9题图
8.东东家有一块等腰三角形的空地ABC,如图,已知E,F分别是边AB,AC的中点,量得AB=AC=12米,BC=10米,他想把四边形BCFE用篱笆围成一圈放养小鸡,则需要篱笆的长是( C )
A.22米 B.24米 C.27米 D.32米
9.【2023·泸州】如图, ABCD的对角线AC,BD相交于点O,∠ADC的平分线与边AB相交于点P,E是PD的中点,若AD=4,CD=6,则EO的长为( A )
A.1 B.2 C.3 D.4
10.如图,在△ABC中,CE是中线,CD是角平分线,AF⊥CD交CD的延长线于点F,AC=7,BC=4,则EF的长为( A )
A.1.5 B.2 C.2.5 D.3
【解析】延长AF,CB交于点G,
∵CD是△ABC的角平分线,∴∠ACF=∠BCF,在△ACF和△GCF中,
∴△ACF≌△GCF(ASA),∴CG=AC=7,AF=FG,∴BG=CG-CB=3,∵AE=EB,AF=FG,∴EF=BG=1.5.
第10题图 第11题图 第12题图
二、填空题
11.如图,在△ABC中,D,E分别是AB,AC的中点,若DE=4,则BC= .
【答案】8
12.如图,在△ABC中,D,E,F分别是AB,AC,BC的中点,若AB=10,AC=8,BC
=12,则△DEF的周长为 .
【答案】15
13.如图,在四边形ABCD中,AB=DC,点P是对角线AC的中点,点M是AD的中点,点N是BC的中点.若∠PMN=20°,则∠MPN的度数为 .
【答案】150°
第13题图 第14题图 第15题图
14.如图,在△ABC中,∠C=90°,E,F分别是AC,BC上的点,AE=16,BF=12,P,Q,D分别是AF,BE,AB的中点,则PQ的长为 .
【答案】10
15.【202广西】如图,在边长为2的正方形ABCD中,E,F分别是BC,CD上的动点,M,N分别是EF,AF的中点,则MN的最大值为 .
【答案】
三、解答题
16.如图,在Rt△ABC中,∠C=90°,∠B=60°,AB=8 cm,E,F分别为边AC,AB的中点.
(1)求∠A的度数;
(2)求EF的长.
解:(1)∠A=30°.
(2)EF=2 cm.
17.如图,在△ABC中,D,E,F分别为边AB,BC,CA的中点.求证:四边形DECF是平行四边形.
证明:∵D,E,F分别为边AB,BC,CA的中点,
∴DF,DE为△ABC的中位线.
∴DF∥BC,DE∥AC,
∴四边形DECF是平行四边形.
18.如图,在△ABC中,D,E分别是AC,AB的中点,点F是CB延长线上的一点,且CF=3BF,连接DB,EF.
(1)求证:四边形DEFB是平行四边形;
(2)若∠ACB=90°,AC=12 cm,DE=4 cm,求四边形DEFB的周长.
解:(1)证明:∵D,E分别是AC,AB的中点,
∴DE是△ABC的中位线,
∴DE∥BC,BC=2DE,
∵CF=3BF,
∴BC=2BF,
∴DE=BF,
又DE∥BF,
∴四边形DEFB是平行四边形.
(2)由(1)得BC=2DE=8(cm),BF=DE=4 cm,四边形DEFB是平行四边形,∴BD=EF,
∵D是AC的中点,AC=12 cm,∴CD=AC=6(cm),
∵∠ACB=90°,
∴BD===10(cm),
∴平行四边形DEFB的周长为2(DE+BD)=2×(4+10)=28(cm).
19.【2023株洲】如图,在△ABC中,点D,E分别为AB,AC的中点,点H在线段CE上,连接BH,点G,F分别为BH,CH的中点.
(1)求证:四边形DEFG为平行四边形;
(2)DG⊥BH,BD=3,EF=2,求线段BG的长度.
(1)【证明】∵点D,E分别为AB,AC的中点,点G,F分别为BH,CH的中点,
∴DE是△ABC的中位线,GF是△HBC的中位线.
∴DE∥BC,DE=BC,GF∥BC,GF=BC.
∴DE∥GF,DE=GF.
∴四边形DEFG为平行四边形.
(2)【解】∵四边形DEFG为平行四边形,
∴DG=EF=2.∵DG⊥BH,∴∠DGB=90°.
∴BG===,
即线段BG的长度为.
20.如图,BD,CE是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别是F,G,连接FG,延长AF,AG,分别与直线BC相交于点M,N.求证:FG=(AB+BC+AC).
【证明】∵BD是∠MBA的平分线,
∴∠ABF=∠MBF.
∵AF⊥BD,∴∠MFB=∠AFB=90°.
∴∠BAF=∠BMF.∴MB=AB.∴AF=MF.
同理可得CN=AC,AG=NG,
∴FG是△AMN的中位线.
∴FG=MN=(MB+BC+CN)=(AB+BC+AC).
21.如图,在四边形ABCD中,对角线AC=BD,E,F分别为AB,CD的中点,连接EF交BD,AC于点P,Q.求证:OP=OQ.
证明:如图,取BC的中点G,连接EG,FG.
∵E,G分别为AB,BC的中点,
∴EG=AC,EG∥AC,
∴∠FEG=∠OQP.
同理,可得FG=BD,FG∥BD,
∴∠EFG=∠OPQ.
∵AC=BD,∴EG=FG,
∴∠FEG=∠EFG,
∴∠OQP=∠OPQ,∴OP=OQ.
