9.3.1 用图象表示变量之间的关系同步练习(含答案)
文档属性
| 名称 | 9.3.1 用图象表示变量之间的关系同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 11.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-04 21:45:42 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第九章 变量之间的关系
3 用图象表示变量之间的关系
第1课时 用图象表示变量之间的关系
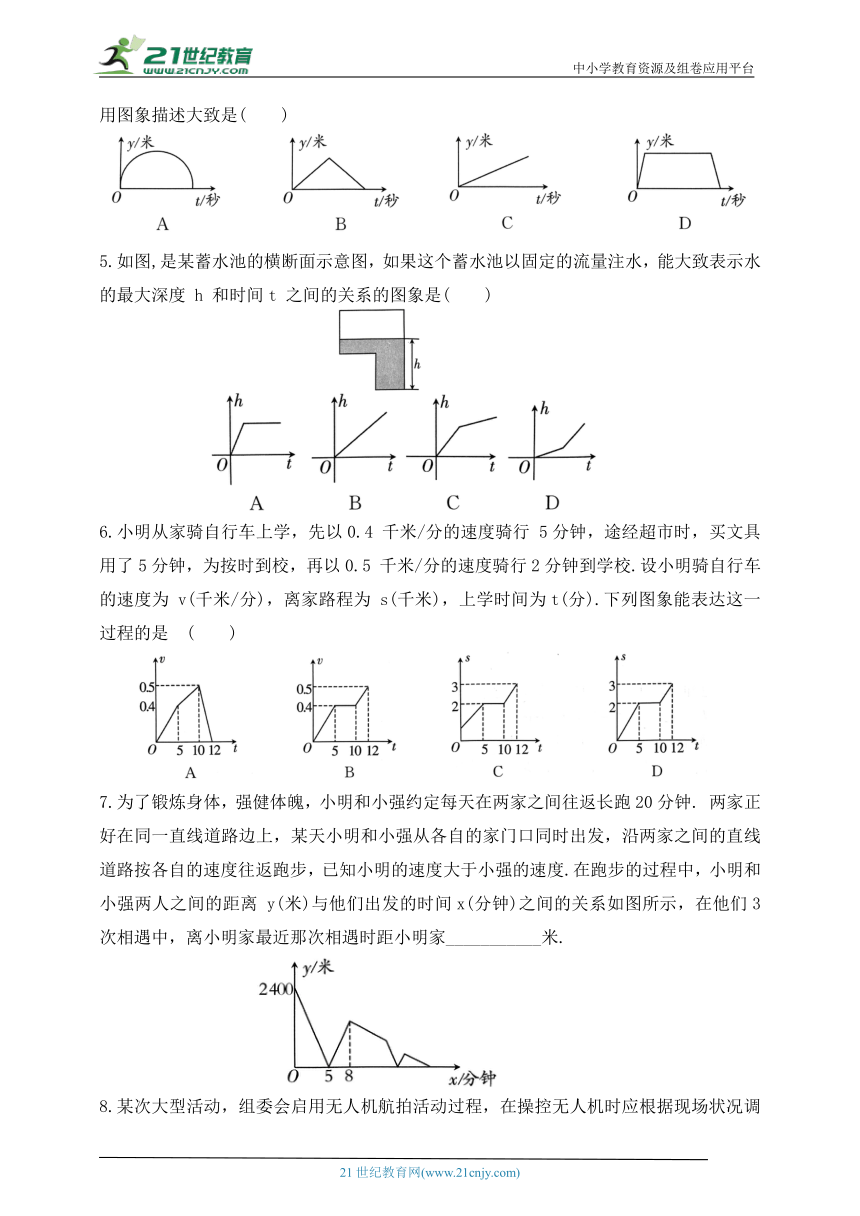
1.如图,折线 OEFPMN 描述了某汽车在行驶过程中速度与时间的关系,下列说法中错误的是 ( )
A.第9分钟时汽车的速度是60千米/时
B.从第 3分钟到第 6分钟,汽车停止
C.从第9分钟到第12 分钟,汽车的速度逐渐减小
D.第12分钟时汽车的速度是 0千米/时
2.早晨嘉嘉去上学,先从家步行到集合点,等几分钟后坐校车去学校,步行和坐校车过程中速度不变.嘉嘉从家到学校所走的路程s(m)与时间 t(min)的大致图象是 ( )
3.如图,把水注入不同的玻璃容器中(设单位时间内进水量相同),那么水面的高度是如何随时间变化的 分别与甲、乙、丙、丁匹配的图象是 ( )
A.(3)(2)(4)(1) B.(2)(3)(1)(4) C.(2)(3)(4)(1) D.(3)(2)(1)(4)
4.南湖隧道是南宁市建成的首条水底隧道.一辆小汽车以一定速度通过南湖隧道,小汽车车身在隧道内的长度记为 y米,小汽车进入隧道的时间记为t秒,则 y与t之间的关系用图象描述大致是( )
5.如图,是某蓄水池的横断面示意图,如果这个蓄水池以固定的流量注水,能大致表示水的最大深度 h 和时间t 之间的关系的图象是( )
6.小明从家骑自行车上学,先以0.4 千米/分的速度骑行 5分钟,途经超市时,买文具用了5分钟,为按时到校,再以0.5 千米/分的速度骑行2分钟到学校.设小明骑自行车的速度为 v(千米/分),离家路程为 s(千米),上学时间为t(分).下列图象能表达这一过程的是 ( )
7.为了锻炼身体,强健体魄,小明和小强约定每天在两家之间往返长跑20分钟. 两家正好在同一直线道路边上,某天小明和小强从各自的家门口同时出发,沿两家之间的直线道路按各自的速度往返跑步,已知小明的速度大于小强的速度.在跑步的过程中,小明和小强两人之间的距离 y(米)与他们出发的时间x(分钟)之间的关系如图所示,在他们3次相遇中,离小明家最近那次相遇时距小明家___________米.
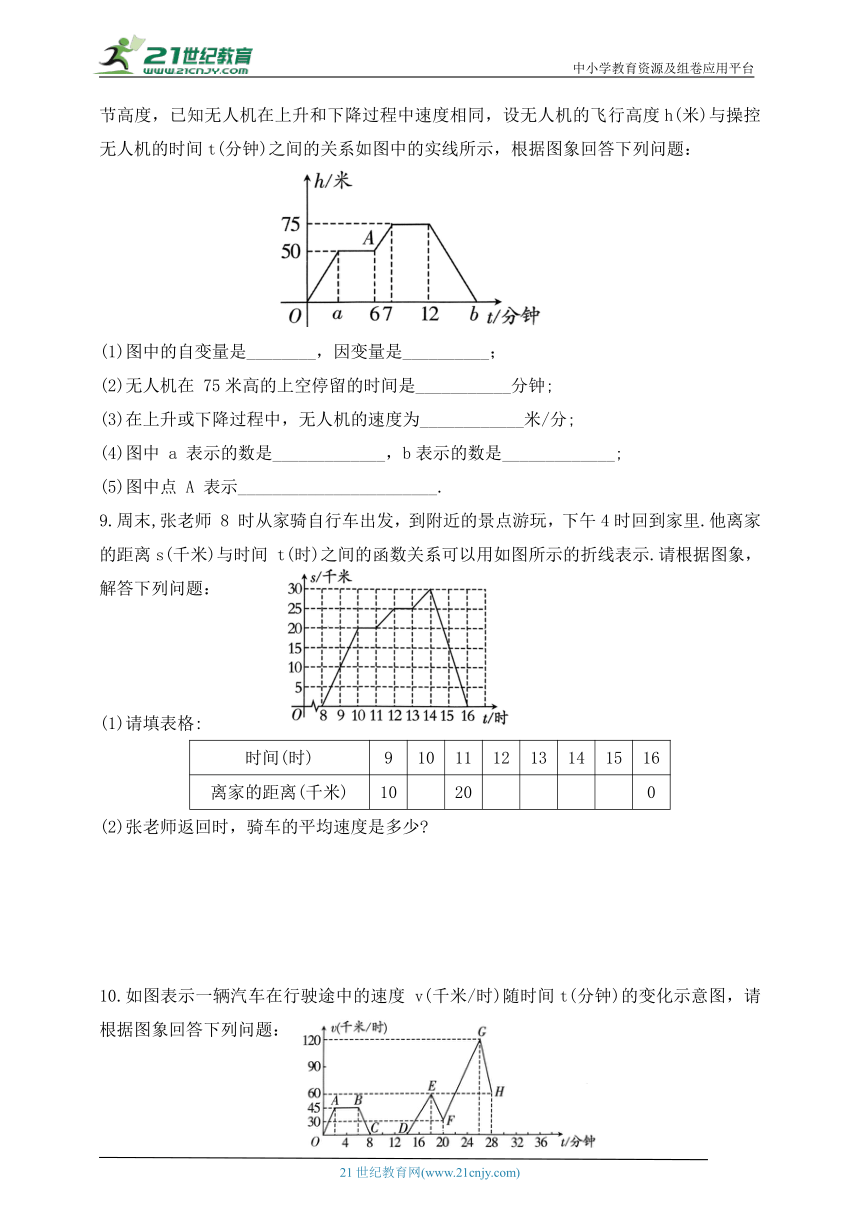
8.某次大型活动,组委会启用无人机航拍活动过程,在操控无人机时应根据现场状况调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图中的实线所示,根据图象回答下列问题:
(1)图中的自变量是________,因变量是__________;
(2)无人机在 75米高的上空停留的时间是___________分钟;
(3)在上升或下降过程中,无人机的速度为____________米/分;
(4)图中 a 表示的数是_____________,b表示的数是_____________;
(5)图中点 A 表示_______________________.
9.周末,张老师 8 时从家骑自行车出发,到附近的景点游玩,下午4时回到家里.他离家的距离s(千米)与时间 t(时)之间的函数关系可以用如图所示的折线表示.请根据图象,解答下列问题:
(1)请填表格:
时间(时) 9 10 11 12 13 14 15 16
离家的距离(千米) 10 20 0
(2)张老师返回时,骑车的平均速度是多少
10.如图表示一辆汽车在行驶途中的速度 v(千米/时)随时间t(分钟)的变化示意图,请根据图象回答下列问题:
(1)汽车速度不变时行驶了________分钟,时速是__________千米/时;
(2)汽车在行驶途中在哪段时间停车休息 休息了多长时间
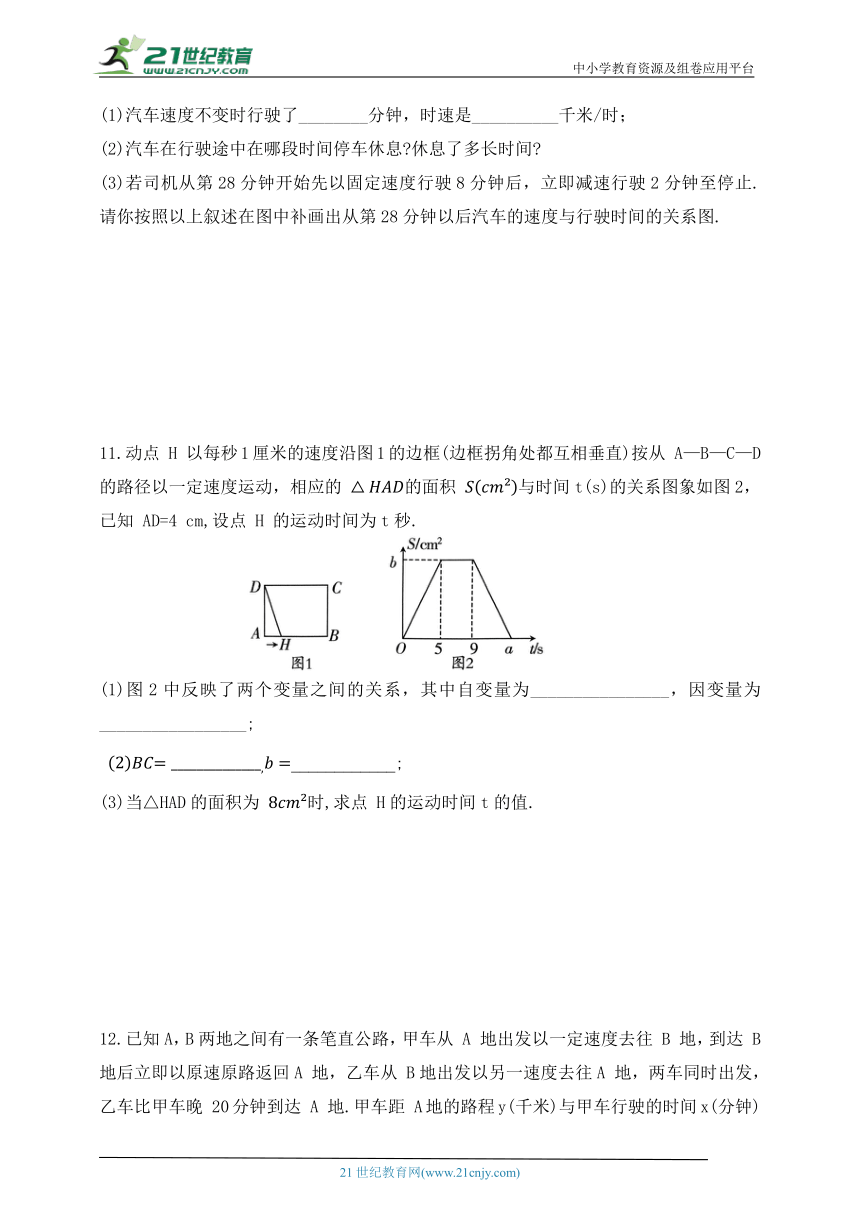
(3)若司机从第28分钟开始先以固定速度行驶8分钟后,立即减速行驶2分钟至停止.请你按照以上叙述在图中补画出从第28分钟以后汽车的速度与行驶时间的关系图.
11.动点 H 以每秒1厘米的速度沿图1的边框(边框拐角处都互相垂直)按从 A—B—C—D的路径以一定速度运动,相应的 的面积 与时间t(s)的关系图象如图2,已知 AD=4 cm,设点 H 的运动时间为t秒.
(1)图2中反映了两个变量之间的关系,其中自变量为________________,因变量为_________________;
____________;
(3)当△HAD的面积为 时,求点 H的运动时间t的值.
12.已知A,B两地之间有一条笔直公路,甲车从 A 地出发以一定速度去往 B 地,到达 B地后立即以原速原路返回A 地,乙车从 B地出发以另一速度去往A 地,两车同时出发,乙车比甲车晚 20分钟到达 A 地.甲车距 A地的路程y(千米)与甲车行驶的时间x(分钟)之间的关系如图所示.
(1)在图中画出乙车距 A 地的路程y(千米)与乙车行驶时间x(分钟)之间的关系图象;
(2)甲、乙两车在行驶过程中相遇了几次
(3)求出乙车距 A 地的路程y(千米)随乙车行驶时间x(分钟)变化的表达式;(不写变量x的取值范围)
(4)求甲车到 B 地时,乙车距A 地的路程.
参考答案
1. B 2. C 3. A 4. D 5. C 6. D
7.300
8.解:(1)操控无人机的时间t,无人机的飞行高度 h;
(2)无人机在 75 米高的上空停留时间为 12-7=5分钟;
故答案为:5;
(3)在上升或下降过程中,无人机的速度为(米/分);
故答案为:25;
(4)图中a表示的数为 (分钟),图中b表示的数为 (分钟);
故答案为:2,15;
(5)在第6分钟时,无人机的飞行高度为50米.
9.解:(1)20,25,25,30,15;
(2)由图象可知张老师返回时,骑车的平均速度是 30÷(16-14)=15(千米/时),
答:张老师返回时,骑车的平均速度是 15 千米/时.
10.解:(1)由图可知,汽车保持速度不变行驶了6-2=4(分钟),时速是45千米/时,故答案为:4,45;
(2)由图可知,汽车在 CD段的速度为0,所以汽车在行驶途中,在 8分钟~14分钟这个时间段停车休息,休息了14-8=6(分钟);
(3)如图所示:
11.解:(1)点 H的运动时间t, 的面积S;
(2)因为动点 H按从A—B—C—D的路径匀速运动,由题意可知,点 H 在 BC 上运动时 的面积不变,所以 则CD=5,所以 4×5=10,故答案为:4 cm,14,10;
(3)当点 H 在 BC 上时,△HAD 的面积为
当△HAD 的面积为8cm 时,可分两种情况:
①当点 H在 AB上时, 则AH=4 cm,所以t=4÷1=4s;
②当点 H在 CD上时, ,则DH=4 cm,所以t=(5+4+5-4)÷1=10s,
综上所述,当点 H的运动时间t为4s 或10s时, 的面积为
12.解:(1)因为乙车比甲车晚20分钟到达A地,所以乙车用80分钟到达 A 地,
画出乙车距A 地的路程y(千米)与x(分钟)之间的关系图象如图:
(2)由图象可知,甲车从A 地去往B 地和到达B地后返回A 地时,分别与乙车各相遇一次,所以甲、乙两车在行驶过程中相遇了2次;
(3)由图象可知,A,B 两地之间的距离为48千米,乙车从 B地出发以一定速度去往A地共用 80分钟,所以乙车的速度为 0.6(千米/分),所以乙车距 A 地的路程y(千米)随乙车行驶时间x(分钟)变化的表达式为 y=48-0.6x;
(4)从图象可知,甲车用 (分钟)到B地,当x=30时,
答:甲车到 B 地时,乙车距 A 地的路程为 30千米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 变量之间的关系
3 用图象表示变量之间的关系
第1课时 用图象表示变量之间的关系
1.如图,折线 OEFPMN 描述了某汽车在行驶过程中速度与时间的关系,下列说法中错误的是 ( )
A.第9分钟时汽车的速度是60千米/时
B.从第 3分钟到第 6分钟,汽车停止
C.从第9分钟到第12 分钟,汽车的速度逐渐减小
D.第12分钟时汽车的速度是 0千米/时
2.早晨嘉嘉去上学,先从家步行到集合点,等几分钟后坐校车去学校,步行和坐校车过程中速度不变.嘉嘉从家到学校所走的路程s(m)与时间 t(min)的大致图象是 ( )
3.如图,把水注入不同的玻璃容器中(设单位时间内进水量相同),那么水面的高度是如何随时间变化的 分别与甲、乙、丙、丁匹配的图象是 ( )
A.(3)(2)(4)(1) B.(2)(3)(1)(4) C.(2)(3)(4)(1) D.(3)(2)(1)(4)
4.南湖隧道是南宁市建成的首条水底隧道.一辆小汽车以一定速度通过南湖隧道,小汽车车身在隧道内的长度记为 y米,小汽车进入隧道的时间记为t秒,则 y与t之间的关系用图象描述大致是( )
5.如图,是某蓄水池的横断面示意图,如果这个蓄水池以固定的流量注水,能大致表示水的最大深度 h 和时间t 之间的关系的图象是( )
6.小明从家骑自行车上学,先以0.4 千米/分的速度骑行 5分钟,途经超市时,买文具用了5分钟,为按时到校,再以0.5 千米/分的速度骑行2分钟到学校.设小明骑自行车的速度为 v(千米/分),离家路程为 s(千米),上学时间为t(分).下列图象能表达这一过程的是 ( )
7.为了锻炼身体,强健体魄,小明和小强约定每天在两家之间往返长跑20分钟. 两家正好在同一直线道路边上,某天小明和小强从各自的家门口同时出发,沿两家之间的直线道路按各自的速度往返跑步,已知小明的速度大于小强的速度.在跑步的过程中,小明和小强两人之间的距离 y(米)与他们出发的时间x(分钟)之间的关系如图所示,在他们3次相遇中,离小明家最近那次相遇时距小明家___________米.
8.某次大型活动,组委会启用无人机航拍活动过程,在操控无人机时应根据现场状况调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图中的实线所示,根据图象回答下列问题:
(1)图中的自变量是________,因变量是__________;
(2)无人机在 75米高的上空停留的时间是___________分钟;
(3)在上升或下降过程中,无人机的速度为____________米/分;
(4)图中 a 表示的数是_____________,b表示的数是_____________;
(5)图中点 A 表示_______________________.
9.周末,张老师 8 时从家骑自行车出发,到附近的景点游玩,下午4时回到家里.他离家的距离s(千米)与时间 t(时)之间的函数关系可以用如图所示的折线表示.请根据图象,解答下列问题:
(1)请填表格:
时间(时) 9 10 11 12 13 14 15 16
离家的距离(千米) 10 20 0
(2)张老师返回时,骑车的平均速度是多少
10.如图表示一辆汽车在行驶途中的速度 v(千米/时)随时间t(分钟)的变化示意图,请根据图象回答下列问题:
(1)汽车速度不变时行驶了________分钟,时速是__________千米/时;
(2)汽车在行驶途中在哪段时间停车休息 休息了多长时间
(3)若司机从第28分钟开始先以固定速度行驶8分钟后,立即减速行驶2分钟至停止.请你按照以上叙述在图中补画出从第28分钟以后汽车的速度与行驶时间的关系图.
11.动点 H 以每秒1厘米的速度沿图1的边框(边框拐角处都互相垂直)按从 A—B—C—D的路径以一定速度运动,相应的 的面积 与时间t(s)的关系图象如图2,已知 AD=4 cm,设点 H 的运动时间为t秒.
(1)图2中反映了两个变量之间的关系,其中自变量为________________,因变量为_________________;
____________;
(3)当△HAD的面积为 时,求点 H的运动时间t的值.
12.已知A,B两地之间有一条笔直公路,甲车从 A 地出发以一定速度去往 B 地,到达 B地后立即以原速原路返回A 地,乙车从 B地出发以另一速度去往A 地,两车同时出发,乙车比甲车晚 20分钟到达 A 地.甲车距 A地的路程y(千米)与甲车行驶的时间x(分钟)之间的关系如图所示.
(1)在图中画出乙车距 A 地的路程y(千米)与乙车行驶时间x(分钟)之间的关系图象;
(2)甲、乙两车在行驶过程中相遇了几次
(3)求出乙车距 A 地的路程y(千米)随乙车行驶时间x(分钟)变化的表达式;(不写变量x的取值范围)
(4)求甲车到 B 地时,乙车距A 地的路程.
参考答案
1. B 2. C 3. A 4. D 5. C 6. D
7.300
8.解:(1)操控无人机的时间t,无人机的飞行高度 h;
(2)无人机在 75 米高的上空停留时间为 12-7=5分钟;
故答案为:5;
(3)在上升或下降过程中,无人机的速度为(米/分);
故答案为:25;
(4)图中a表示的数为 (分钟),图中b表示的数为 (分钟);
故答案为:2,15;
(5)在第6分钟时,无人机的飞行高度为50米.
9.解:(1)20,25,25,30,15;
(2)由图象可知张老师返回时,骑车的平均速度是 30÷(16-14)=15(千米/时),
答:张老师返回时,骑车的平均速度是 15 千米/时.
10.解:(1)由图可知,汽车保持速度不变行驶了6-2=4(分钟),时速是45千米/时,故答案为:4,45;
(2)由图可知,汽车在 CD段的速度为0,所以汽车在行驶途中,在 8分钟~14分钟这个时间段停车休息,休息了14-8=6(分钟);
(3)如图所示:
11.解:(1)点 H的运动时间t, 的面积S;
(2)因为动点 H按从A—B—C—D的路径匀速运动,由题意可知,点 H 在 BC 上运动时 的面积不变,所以 则CD=5,所以 4×5=10,故答案为:4 cm,14,10;
(3)当点 H 在 BC 上时,△HAD 的面积为
当△HAD 的面积为8cm 时,可分两种情况:
①当点 H在 AB上时, 则AH=4 cm,所以t=4÷1=4s;
②当点 H在 CD上时, ,则DH=4 cm,所以t=(5+4+5-4)÷1=10s,
综上所述,当点 H的运动时间t为4s 或10s时, 的面积为
12.解:(1)因为乙车比甲车晚20分钟到达A地,所以乙车用80分钟到达 A 地,
画出乙车距A 地的路程y(千米)与x(分钟)之间的关系图象如图:
(2)由图象可知,甲车从A 地去往B 地和到达B地后返回A 地时,分别与乙车各相遇一次,所以甲、乙两车在行驶过程中相遇了2次;
(3)由图象可知,A,B 两地之间的距离为48千米,乙车从 B地出发以一定速度去往A地共用 80分钟,所以乙车的速度为 0.6(千米/分),所以乙车距 A 地的路程y(千米)随乙车行驶时间x(分钟)变化的表达式为 y=48-0.6x;
(4)从图象可知,甲车用 (分钟)到B地,当x=30时,
答:甲车到 B 地时,乙车距 A 地的路程为 30千米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
