第1-4单元应用题综合训练-数学五年级下册苏教版(含解析)
文档属性
| 名称 | 第1-4单元应用题综合训练-数学五年级下册苏教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 486.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-06 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第1-4单元应用题综合训练-数学五年级下册苏教版
1.动物园里长颈鹿的身高6米,比大猩猩高4.35米,大猩猩的身高是多少米?(用方程解)
2.在12张球桌上同时进行乒乓球比赛,双打的比单打的多6人。进行单打和双打比赛的乒乓球桌各有几张?
3.果园里桃树的棵数是梨树的5倍,比梨树多60棵。桃树和梨树各有多少棵?
(1)根据题意写出等量关系式。
(2)用方程解答。
4.学校派王老师去购买篮球和足球,购买单据如图。王老师买了多少个足球?(用方程解答)
(小贴士数字的大写:零壹贰叁肆伍陆柒捌玖)
5.在大同市第四届保护母亲河一一万泉河净水公益活动中,云冈区有0.36万名志愿者参加,比平城区志愿者人数的2倍少0.2万名;云州区比新荣区多0.18万名,云州区的人数是新荣区的1.5倍。
问题一:平城区志愿者有多少万名?
问题二:云州区志愿者有多少万名?
①选问题:我选择的问题是:( )。
②根据所选问题完成下面两个任务。
任务一:根据数量间的相等关系写出等量关系式。
任务二:根据以上数量间的相等关系列方程解决所选问题。
6.小汽车和摩托车同时从两地相向开出,小汽车每小时行80千米,经过3小时已驶过中点30千米,此时小汽车与摩托车正好相遇。摩托车每小时行多少千米?
7.学校图书馆购进文艺书和科技书共320本,其中文艺书的本数是科技书的4倍,文艺书、科技书各有多少本?(用方程解)
8.国庆期间,李华一家5个大人和2个孩子去宁波花博园游览,儿童票价是成人票价的一半,共付门票费270元,花博园的儿童票和成人票分别为多少元?(列方程解答)
9.小宁、小玲和小亮共有邮票180张,小宁说:我的邮票是小玲的2倍,小玲说:我的邮票最少,小亮说:我的邮票是他俩的总和。他们各有邮票多少张?
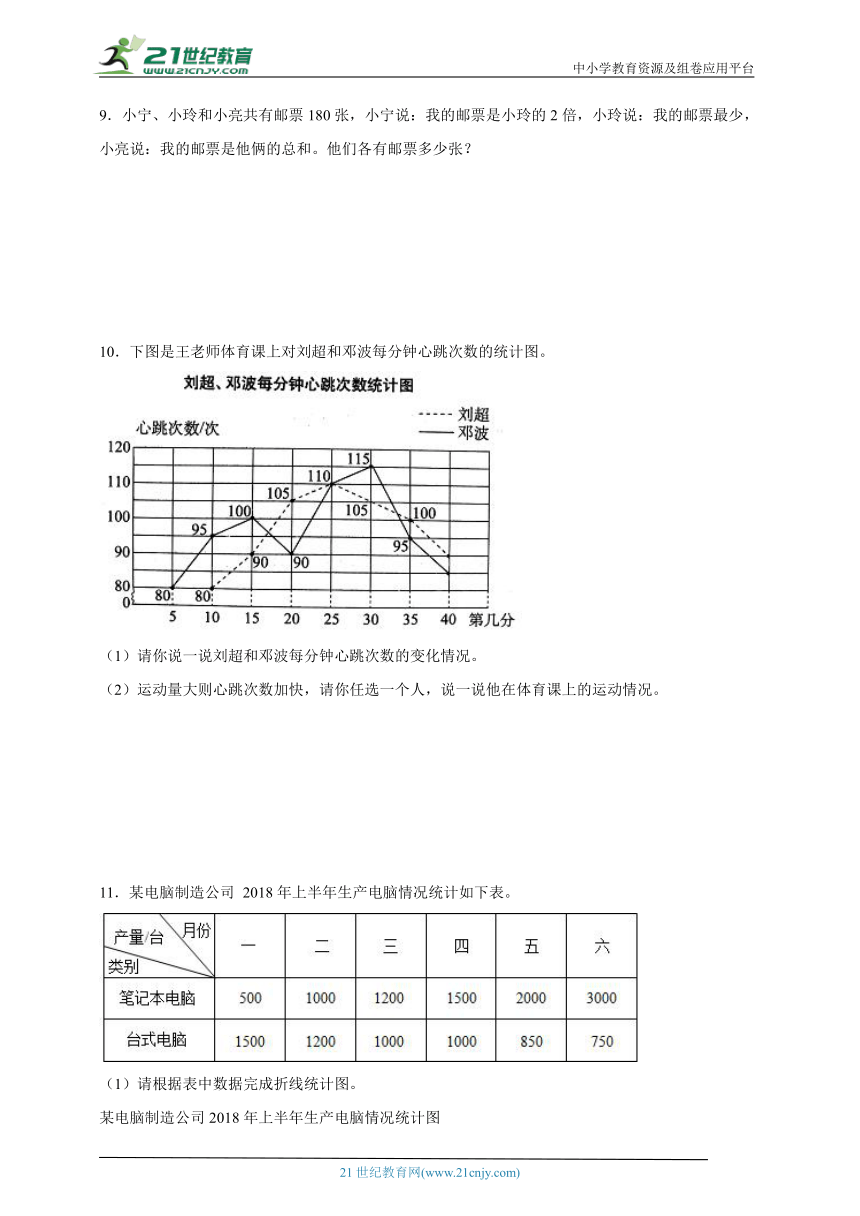
10.下图是王老师体育课上对刘超和邓波每分钟心跳次数的统计图。
(1)请你说一说刘超和邓波每分钟心跳次数的变化情况。
(2)运动量大则心跳次数加快,请你任选一个人,说一说他在体育课上的运动情况。
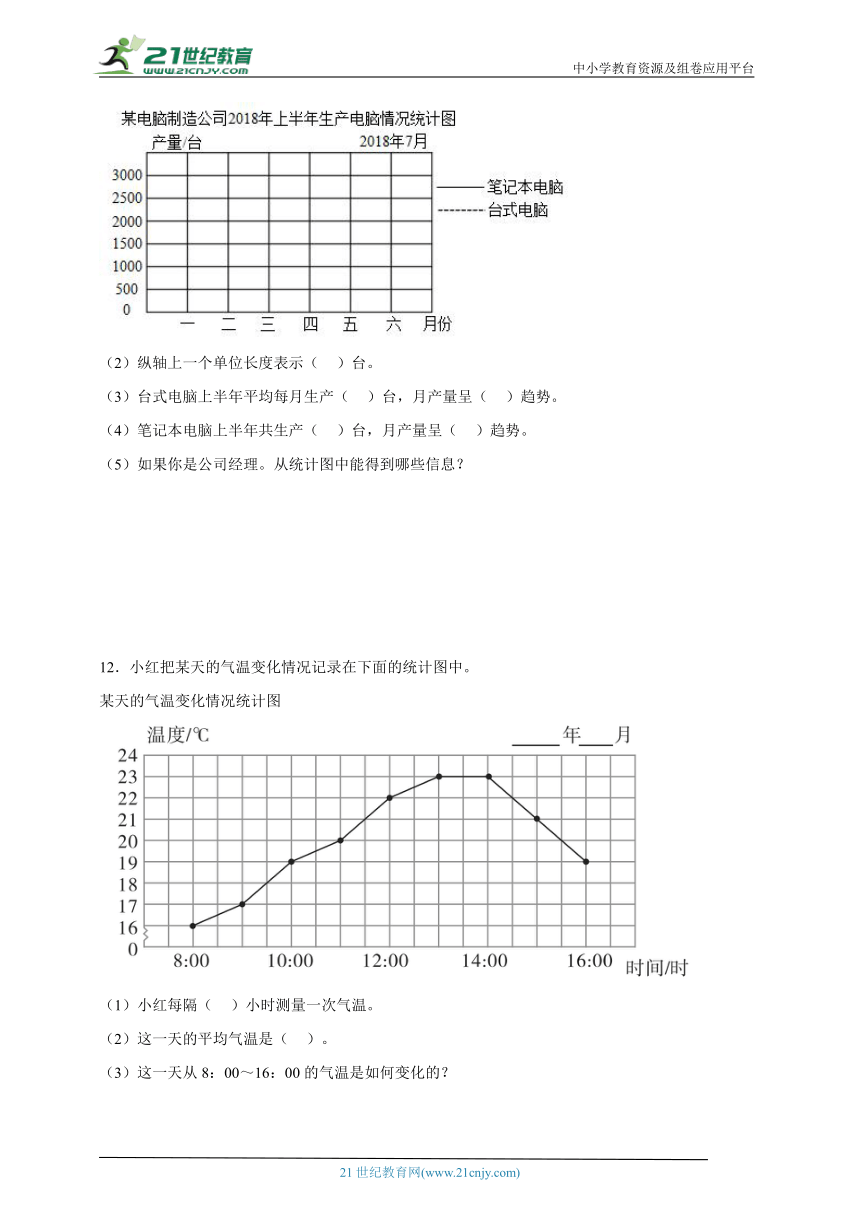
11.某电脑制造公司 2018年上半年生产电脑情况统计如下表。
(1)请根据表中数据完成折线统计图。
某电脑制造公司2018年上半年生产电脑情况统计图
(2)纵轴上一个单位长度表示( )台。
(3)台式电脑上半年平均每月生产( )台,月产量呈( )趋势。
(4)笔记本电脑上半年共生产( )台,月产量呈( )趋势。
(5)如果你是公司经理。从统计图中能得到哪些信息?
12.小红把某天的气温变化情况记录在下面的统计图中。
某天的气温变化情况统计图
(1)小红每隔( )小时测量一次气温。
(2)这一天的平均气温是( )。
(3)这一天从8:00~16:00的气温是如何变化的?
13.为了从甲、乙两名学生中选拔一人参加今年六月份的全县小学生数学竞赛,每个月对他们的学进行一次测验,下图是两人赛前5次测验成绩的折线统计图。
(1)分别求出甲、乙两名学生5次测验的平均成绩。
(2)如果你是他们的辅导教师,应选派哪名学生参加这次数学竞赛。请说明理由。
14.暑假期间,小林每6天游泳一次,小军每8天游泳一次。7月24日两人在游池相遇,八月几日他们再次相遇?
15.李小明家卫生间的地面是一个长300厘米,宽240厘米的长方形,如果给卫生间的地面铺上地砖,选择下面哪种规格的地砖能正好铺满?请简要说明理由。
16.五年级(2)班同学站队,4人一排,5人一排,6人一排都没有剩余。五年级(2)班至少有学生多少人?
17.一包糖果在100粒以内,每3粒一数余1粒,每4粒一数也余1粒,每5粒一数还余1粒,请问这包糖果共有多少粒?
18.一个长方形的池塘,长60米,宽42米,如果在它的四周及四角栽柳树,每相邻两棵树之间的距离要相等,那么最少要栽多少棵?如果每两棵柳树之间栽2棵桃树,那么桃树一共栽了多少棵?
19.用若干个长15厘米、宽12厘米的小长方形,按照下图的样子拼成一个大正方形。
(1)这个大正方形的边长最少是多少厘米?
(2)拼成这个大正方形,至少需要多少个这样的小长方形?
20.有一根5米长的彩带剪了四次,每段长多少米?每段占全长的多少?
21.一串彩旗共57面,按照1红2黄1绿的顺序排列。绿色彩旗是红色彩旗的几分之几?
22.一个榨油厂用100千克花生榨了42千克花生油,平均1千克花生油要用多少千克花生?用1千克花生可以榨多少千克花生油?
23.修路队要修筑一条长500米的水泥路,已修了225米,已修了全长的几分之几?
24.幼儿园运来3箱饼干,一共60千克。平均分给4个班。
(1)每个班分到多少千克?
(2)每个班分到多少箱?
25.5个小朋友吃了2盒饼干,每盒4千克。
(1)平均每个小朋友吃了几分之几盒饼干?
(2)平均每个小朋友吃了这些饼干的几分之几?
参考答案:
1.1.65米
【分析】可以设大猩猩的身高为x米,由于大猩猩的身高+4.35=长颈鹿的身高,据此即可列出方程,再根据等式的性质求解即可。
【详解】解:设大猩猩的身高是x米。
x+4.35=6
x=6-4.35
x=1.65
答:大猩猩的身高是1.65米。
【点睛】本题主要考查列方程解应用题,关键是找准等量关系是解题的关键。
2.双打:5张,单打:7张
【分析】设进行双打比赛的乒乓球桌有x张,则进行单打比赛的乒乓球桌有(12-x)张;双打4人比赛,x张桌有4x人,单打比赛有2人,单打人数有2×(12-x)人,双打比单打多6人,即双打比赛人数-单打比赛人数=6,列方程:4x-2×(12-x)=6,解方程,即可解答。
【详解】解:设进行双打比赛乒乓球桌有x张,则进行单打比赛乒乓球桌有(12-x)张。
4x-2×(12-x)=6
4x-24+2x=6
6x=6+24
6x=30
x=30÷6
x=5
单打:12-5=7(张)
答:进行双打比赛的乒乓球桌5张,单打比赛的乒乓球桌7张。
【点睛】本题考查方程的实际应用,利用单打桌张数与双打桌张数之间的关系,设出未知数,再根据双打人数与单打人数,找出它们之间相关的量,列方程,解方程。
3.(1)桃树的棵数-梨树的棵数=60
(2)梨树有15棵;桃树有75棵
【分析】根据题意“桃树的棵数是梨树的5倍”设梨树有x棵,则桃树有5x棵,由“桃树的棵数是梨树的5倍,比梨树多60棵”可知:桃树的棵数-梨树的棵数=60,据此列方程解答。
【详解】(1)桃树的棵数-梨树的棵数=60
(2)解:设梨树有x棵,则桃树有5x棵。
5x-x=60
4x=60
x=15
15+60=75(棵)
答:梨树有15棵,桃树有75棵。
【点睛】此题主要考查了列方程解应用题,弄清题意,找出合适的等量关系,进而列出方程是解答此类问题的关键。
4.5个
【分析】根据题意可得等量关系式:篮球的总价+足球的总价=815元,然后列方程解答即可。
【详解】解:设王老师买了x个足球。
55×8+75x=815
440+75x=815
75x=375
x=5
答:王老师买了5个足球。
【点睛】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题。
5.我选择的问题是:问题一。平城区志愿者人数×2倍-0.2万=0.36万;0.28万名。
【分析】问题一:根据题意,设平城区志愿者有x万名,云冈区有0.36万名志愿者参加,根据云冈区比比平城区志愿者人数的2倍少0.2万名,即可得到方程(2x-0.2)=0.36,然后解方程,即可得到平城区志愿者有多少万名;
问题二:已知云州区志愿者比新荣区多0.18万名,云州区的人数是新荣区的1.5倍。设新荣区志愿者有y万名,可得出方程:1.5y-y=0.18。
【详解】我选择的问题是:问题一。
平城区志愿者人数×2倍-0.2万=0.36万
解:设平城区志愿者有x万名。
2x-0.2=0.36
2x-0.2+0.2=0.36+0.2
2x÷2=0.56÷2
x=0.28
答:平城区志愿者有0.28万名。
我选择的问题是问题二:云州区志愿者有多少万名?
云州区志愿者人数-新荣区志愿者人数=0.18
解:设新荣区志愿者有y万名。
1.5y-y=0.18
0.5y=0.18
0.5y÷0.5=0.18÷0.5
y=0.36
0.36×1.5=0.54(万名)
答:云州区志愿者有0.54万名。
【点睛】利用方程解决问题的关键是找准题目中的等量关系。
6.60千米
【分析】根据题意,经过3小时,小汽车行驶80×3=240千米,用240-30=210千米,求出两地的一半的距离是210千米,再用210×2,求出两地的距离;设摩托车每小时行x千米,摩托车3小时行3x千米,小汽车3小时行80×3千米,摩托车行驶的路程+小汽车行驶的路程=两地的距离,列方程:3x+80×3=(80×3-30)×2,解方程,即可解答。
【详解】解:设摩托车每小时行x千米。
3x+80×3=(80×3-30)×2
3x+240=(240-30)×2
3x+240=210×2
3x+240=420
3x=420-240
3x=180
x=180÷3
x=60
答:摩托车每小时行60千米。
【点睛】本题考查方程的实际应用,利用速度、时间和距离三者关系,设出未知数,找出相关的量,列方程,解方程,关键是求出两地之间的距离。
7.文艺书:256本;科技数64本
【分析】设科技书有x本,则文艺书有4x本;根据文艺书和科技书共320本列出方程求出科技书的本数,进而得出文艺书的本数;据此解答。
【详解】解:设科技书有x本,则文艺书有4x本。
x+4x=320
5x=320
5x÷5=320÷5
x=64
4x=4×64=256
答:文艺书有256本,科技数有64本。
【点睛】本题主要考查列方程解含有两个未知数的问题,找出等量关系式是解题的关键。
8.儿童票:22.5元;成人票:45元
【分析】根据题意,儿童票是成人票的一半,设儿童票为x元,则成人票为2x元,5个大人,票价为(2x×5)元;2个孩子,2个孩子票价为2x元;一共付门票270元,即2个孩子票价钱+5个大人票价=270元,列方程:2x+2x×5=270,解方程,求出儿童票价钱,进而求出成人票价。
【详解】解:设儿童票x元,则成人票2x元。
2x+2x×5=270
2x+12x=270
12x=270
x=270÷12
x=22.5
成人票:22.5×2=45(元)
答:花博园的儿童票22.5元,成人票45元。
【点睛】根据方程的实际应用,利用儿童票价与成人票价之间的关系,设出未知数,找出相关的量,列方程,解方程。
9.小玲:30张;小宁:60张;小亮:90张
【分析】设小玲有邮票x张;小宁的邮票是小玲的2倍,小宁有邮票2x张,小亮的邮票是小玲和小宁的邮票的和,即小亮有邮票(x+2x)张,他们共有邮票180张,列方程:x+2x+(x+2x)=180,解方程,即可解答。
【详解】设小玲有邮票x张,则小宁有邮票2x张,小亮有邮票x+2x张。
x+2x+(x+2x)=180
3x+3x=180
6x=180
x=180÷6
x=30
小宁:30×2=60(张)
小亮:30+30×2
=30+60
=90(张)
答:小玲有邮票30张,小宁有邮票60张,小亮有邮票90张。
【点睛】本题考查方程的实际应用,根据小玲、小宁、小亮三人邮票张数之间的关系,设出未知数,找出相关的量,列方程,解方程。
10.(1)刘超在上课第10分钟开始心跳逐渐加快,在第25分钟时达到最快,之后又开始下降;邓波的心跳在上课第5分钟开始加快,在第15分钟时达到每分钟100次,之后又开始下降,第20分钟时达到每分钟90次,之后又开始加快,在第30分钟时达到最快,之后又急剧下降。
(2)刘超从第10分钟开始运动,在第25分钟时停止运动,(不唯一)
【分析】(1)根据折线统计图,依次对两个人进行分析上升表示心跳加快,下降表示心跳减慢,分段分析即可。(2)线段上升表示在运动,线段下降表示运动减慢或停止运动,据此任找一人分析即可。
【详解】(1)刘超在上课第10分钟开始心跳逐渐加快,在第25分钟时达到最快,之后又开始下降;邓波的心跳在上课第5分钟开始加快,在第15分钟时达到每分钟100次,之后又开始下降,第20分钟时达到每分钟90次,之后又开始加快,在第30分钟时达到最快,之后又急剧下降。
(2)刘超从第10分钟开始运动,在第25分钟时停止运动,(不唯一)
【点睛】此题要求学生自己描述折线统计图中体现的相关信息,难度相对较大,注意语言表述的准确性。
11.(1)图见详解
(2)500;
(3)1050;下降;
(4)9200;上升;
(5)见详解
【分析】(1)根据表中的数据完成复式折线统计图即可;
(2)从统计图可知,纵轴从0到500,即可得知一个单位长度;
(3)用台式电脑上半年6个月的制造总台数除以6得出平均台数,根据折线图走势可知月产量趋势;
(4)将笔记本电脑上半年6个月的制造台数相加即可,根据折线图走势可知月产量趋势;
(5)根据统计图台式电脑和笔记本电脑的生产趋势,进行解答,合理即可。
【详解】(1)如下图:
(2)纵轴上一个单位长度表示500台;
(3)(1500+1200+1000+1000+850+750)÷6
=6300÷6
=1050(台)
根据统计图可知,台式电脑月产量呈下降趋势;
(4)500+1000+1200+1500+2000+3000
=2700+6500
=9200(台)
根据统计图可知,笔记本电脑月产量呈上升趋势;
(5)答:台式电脑的产量逐步下降,笔记本电脑的产量不断上升,且笔记本电脑的产量已经远超过台式电脑的产量,表明笔记本电脑的市场需求量远大于台式电脑。在生产的安排上可以适当多生产笔记本电脑,少生产台式电脑,避免过多剩余(言之有理即可)。
【点睛】解答此题的关键利用图中已知的信息,结合给出的条件,求得各部分数据解决问题;需要熟练掌握平均数=总量÷份数的平均数公式。
12.(1)1
(2)20℃
(3)这一天从8:00~16:00的气温先上升后下降。
【分析】(1)根据点的间隔,观察统计图横轴填空;
(2)将所有温度加起来÷9即可;
(3)根据折线的趋势作答即可。
【详解】(1)小红每隔( 1 )小时测量一次气温。
(2)(16+17+19+20+22+23+23+21+19)÷9
=180÷9
=20(℃)
这一天的平均气温是( 20℃ )。
(3)这一天从8:00~16:00的气温先上升后下降。
【点睛】本题考查了折线统计图的应用和分析,平均数=总数÷份数。
13.(1)甲:80;乙:80。
(2)选乙参加,因为甲乙两人成绩的平均数相等,但乙的成绩方差小,故比较稳定。
【分析】(1)根据平均数的计算方法,结合折线图读出数据可得答案。
(2)根据折线图,由于两人的平均数相等,即总体水平相同,再比较方差,选方差小的参加。
【详解】(1)甲平均数:(65+80+80+85+90)÷5=400÷5=80;
乙平均数:(70+90+85+75+80)÷5=400÷5=80;
答:甲学生5次测验的平均成绩80分,乙学生5次测验的平均成绩80分。
(2)甲方差:[(65-80)+(80-80)+(80-80)+(85-80)+(90-80)]÷5
=(225+25+100)÷5
=350÷5
=70
乙方差:[(70-80)+(90-80)+(85-80)+(75-80)+(80-80)]÷5
=(100+100+25+25)÷5
=250÷5
=50
70>50
答:由以上可知,甲乙两人成绩的平均数相等,但乙的成绩方差小,故比较稳定,故选乙参加。
【点睛】本题考查平均数、方差的计算及折线统计图的运用,折线统计图表示的是事物的变化情况,在做的过程中要注意细节。
14.8月17日
【分析】小林每6天游泳一次,小军每8天游泳一次,6和8的最小公倍数就是他们相遇两次之间间隔的时间;从7月24日向后推算这个天数即可。
【详解】6=2×3,8=2×2×2,6和8的最小公倍数是:2×2×2×3=24,所以他们每相隔24天见一次面;7月24日再过24天是8月17日。
答:8月17日他们又再次相遇。
【点睛】本题关键是找出他们每两次相遇之间相隔的天数,进而根据开始的天数推算求解。
15.边长60cm的地砖正好铺满,理由见解析。
【分析】根据题意可以计算出卫生间的总面积,除以地砖面积,没有余数说明正好铺满,有余数说明不能正好铺满。
【详解】300×240=72000(平方厘米)
50×50=2500(平方厘米)
72000÷2500=28(块)……2000(平方厘米)
边长为50厘米时,有余数,不能正好铺满。
60×60=3600(平方厘米)
72000÷3600=20(块)
边长为50厘米时,没有余数,能正好铺满。
答:边长60cm的地砖正好铺满。需要用20块。
【点睛】此题还可以从另一个角度思考:装好铺满,说明地砖的边长是300和240的公因数,据此可以推断正好铺满的是边长60厘米的地砖。
16.60人
【分析】求出三种站法每排人数的最小公倍数就是最少人数。
【详解】4=2×2
6=2×3
2×2×3×5=60(人)
答:五年级(2)班至少有学生60人。
【点睛】全部公有的质因数和各自独立的质因数,它们连乘的积就是这几个数的最小公倍数。
17.61粒
【分析】由题意可知:糖果的数量是3、4、5的公倍数+1
【详解】3、4、5的最小公倍是60
60+1<100
所以这包糖果共有61粒。
答:这包糖果共有61粒。
【点睛】本题主要考查公倍数的实际应用。
18.34棵;68棵
【分析】(1)要求最少要栽多少棵,即每相邻两棵树之间的距离最大,即相邻两棵树之间的距离是60和42的最大公因数,求出60和42的最大公因数,即相邻两棵树之间的距离,即可求出应栽树的棵数;
(2)因为此长方形的池塘四周及四角栽柳树,可以看成是一个封闭的图形,所栽的柳树的棵数和间距数相等,用间距乘2即可解答出所种的桃树的棵数。
【详解】60=2×2×3×5
42=2×3×7
60、42的最大公因数是2×3=6
(60+42)×2÷6
=102×2÷6
=204÷6
=34(棵)
34×2=68(棵)
答:最少要种14棵柳树,桃树一共栽了68棵。
【点睛】关键是理解题意,明白是从求公因数作为突破口,进而找出解决问题的方法。
19.(1)60厘米
(2)20个
【分析】(1)由题意知:拼成的大正方形的边长既是15的倍数,也是12的倍数。求得15和12的最小公倍数既是大正方形的边长。
(2)在大正方形中,一行可以摆60÷15=4个小长方形,一共可以摆60÷12=5行,所以一共可以摆4×5=20(个)
【详解】(1)15=3×5
12=2×2×3
15和12的最小公倍数是:2×2×3×5=60
答:这个大正方形的边长最少60厘米。
(2)60÷15=4(个)
60÷12=5(行)
4×5=20(个)
答:至少需要20个这样的小长方形。
【点睛】明确大正方形的边长是小长方形长和宽的最小公倍数,再求得大正方形中一行可以摆几个,可以摆几行是解答本题的关键。
20.1米;
【分析】减了4次就是剪成5段,求每段的长度,用除法即可;求每段占全长的几分之几,是把这根彩带的长度看作单位“1”,把它平均分成5份,每份占全长的。
【详解】5÷5=1(米)
1÷5=
答:每段长1米,每段占全长的。
【点睛】本题是一道易错题,主要考查对分数意义的理解。
21.
【分析】根据题意可知,1红2黄1绿4个颜色排列为一组循环,那么用57÷4即可求出几组循环和剩余几面彩旗,这样分别求出红色和绿色的彩旗数量,再根据求一个数是另一个数的几分之几用除法即可解答。
【详解】57÷4=14(组)……1(面)
红色彩旗:14×1+1=15(面)
绿色彩旗:14×1=14(面)
14÷15=
答:绿色彩旗是红色彩旗的。
【点睛】此题考查了学生对周期问题的理解与应用,以及求一个数是另一个数的几分之几的应用解法。
22.千克;千克
【分析】求1千克花生油所用花生重量,用花生重量除以花生油重量;求1千克花生所用花生油重量,用花生油重量除以花生重量。
【详解】(1)100÷42=(千克)
答:平均1千克花生油要用千克花生。
(2)42÷100=(千克)
答:用1千克花生可以榨千克花生油。
【点睛】此题主要考查学生对分数应用的实际解题能力。注意区分两问的不同:求榨油一千克油需要花生的重量是把花生的重量平均分;求每千克花生榨油的重量是把油重量平均分。
23.
【分析】求一个数是另一个数的几分之几,用除法,即用已修的路除以全长即可。
【详解】225÷500=
答:已修了全长的。
【点睛】此题主要考查学生对分数的实际应用解题能力,需要掌握求一个数是另一个数的几分之几,用除法。
24.(1)15千克
(2)箱
【分析】(1)用这3箱饼干的重量除以班级个数,即可求出每个班分到多少千克;
(2)用饼干箱数除以班级个数,即可求出每个班分到多少箱。
【详解】(1)60÷4=15(千克)
答:每个班分到15千克。
(2)3÷4=(箱)
答:每个班分到箱。
【点睛】考查了除法的意义,分数与除法的关系,学生要理解掌握。
25.(1)盒
(2)
【分析】(1)用饼干总盒数除以总人数就是平均每个小朋友吃了几分之几盒饼干;
(2)把饼干总质量看作单位“1”,用1除以总人数就是平均每个小朋友吃了这些饼干的几分之几。
【详解】(1)2÷5=(盒)
答:平均每个小朋友吃了盒饼干。
(2)1÷5=
答:平均每个小朋友吃了这些饼干的。
【点睛】解答本题要区分:第一问求的是数量;第二问求的是分率。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第1-4单元应用题综合训练-数学五年级下册苏教版
1.动物园里长颈鹿的身高6米,比大猩猩高4.35米,大猩猩的身高是多少米?(用方程解)
2.在12张球桌上同时进行乒乓球比赛,双打的比单打的多6人。进行单打和双打比赛的乒乓球桌各有几张?
3.果园里桃树的棵数是梨树的5倍,比梨树多60棵。桃树和梨树各有多少棵?
(1)根据题意写出等量关系式。
(2)用方程解答。
4.学校派王老师去购买篮球和足球,购买单据如图。王老师买了多少个足球?(用方程解答)
(小贴士数字的大写:零壹贰叁肆伍陆柒捌玖)
5.在大同市第四届保护母亲河一一万泉河净水公益活动中,云冈区有0.36万名志愿者参加,比平城区志愿者人数的2倍少0.2万名;云州区比新荣区多0.18万名,云州区的人数是新荣区的1.5倍。
问题一:平城区志愿者有多少万名?
问题二:云州区志愿者有多少万名?
①选问题:我选择的问题是:( )。
②根据所选问题完成下面两个任务。
任务一:根据数量间的相等关系写出等量关系式。
任务二:根据以上数量间的相等关系列方程解决所选问题。
6.小汽车和摩托车同时从两地相向开出,小汽车每小时行80千米,经过3小时已驶过中点30千米,此时小汽车与摩托车正好相遇。摩托车每小时行多少千米?
7.学校图书馆购进文艺书和科技书共320本,其中文艺书的本数是科技书的4倍,文艺书、科技书各有多少本?(用方程解)
8.国庆期间,李华一家5个大人和2个孩子去宁波花博园游览,儿童票价是成人票价的一半,共付门票费270元,花博园的儿童票和成人票分别为多少元?(列方程解答)
9.小宁、小玲和小亮共有邮票180张,小宁说:我的邮票是小玲的2倍,小玲说:我的邮票最少,小亮说:我的邮票是他俩的总和。他们各有邮票多少张?
10.下图是王老师体育课上对刘超和邓波每分钟心跳次数的统计图。
(1)请你说一说刘超和邓波每分钟心跳次数的变化情况。
(2)运动量大则心跳次数加快,请你任选一个人,说一说他在体育课上的运动情况。
11.某电脑制造公司 2018年上半年生产电脑情况统计如下表。
(1)请根据表中数据完成折线统计图。
某电脑制造公司2018年上半年生产电脑情况统计图
(2)纵轴上一个单位长度表示( )台。
(3)台式电脑上半年平均每月生产( )台,月产量呈( )趋势。
(4)笔记本电脑上半年共生产( )台,月产量呈( )趋势。
(5)如果你是公司经理。从统计图中能得到哪些信息?
12.小红把某天的气温变化情况记录在下面的统计图中。
某天的气温变化情况统计图
(1)小红每隔( )小时测量一次气温。
(2)这一天的平均气温是( )。
(3)这一天从8:00~16:00的气温是如何变化的?
13.为了从甲、乙两名学生中选拔一人参加今年六月份的全县小学生数学竞赛,每个月对他们的学进行一次测验,下图是两人赛前5次测验成绩的折线统计图。
(1)分别求出甲、乙两名学生5次测验的平均成绩。
(2)如果你是他们的辅导教师,应选派哪名学生参加这次数学竞赛。请说明理由。
14.暑假期间,小林每6天游泳一次,小军每8天游泳一次。7月24日两人在游池相遇,八月几日他们再次相遇?
15.李小明家卫生间的地面是一个长300厘米,宽240厘米的长方形,如果给卫生间的地面铺上地砖,选择下面哪种规格的地砖能正好铺满?请简要说明理由。
16.五年级(2)班同学站队,4人一排,5人一排,6人一排都没有剩余。五年级(2)班至少有学生多少人?
17.一包糖果在100粒以内,每3粒一数余1粒,每4粒一数也余1粒,每5粒一数还余1粒,请问这包糖果共有多少粒?
18.一个长方形的池塘,长60米,宽42米,如果在它的四周及四角栽柳树,每相邻两棵树之间的距离要相等,那么最少要栽多少棵?如果每两棵柳树之间栽2棵桃树,那么桃树一共栽了多少棵?
19.用若干个长15厘米、宽12厘米的小长方形,按照下图的样子拼成一个大正方形。
(1)这个大正方形的边长最少是多少厘米?
(2)拼成这个大正方形,至少需要多少个这样的小长方形?
20.有一根5米长的彩带剪了四次,每段长多少米?每段占全长的多少?
21.一串彩旗共57面,按照1红2黄1绿的顺序排列。绿色彩旗是红色彩旗的几分之几?
22.一个榨油厂用100千克花生榨了42千克花生油,平均1千克花生油要用多少千克花生?用1千克花生可以榨多少千克花生油?
23.修路队要修筑一条长500米的水泥路,已修了225米,已修了全长的几分之几?
24.幼儿园运来3箱饼干,一共60千克。平均分给4个班。
(1)每个班分到多少千克?
(2)每个班分到多少箱?
25.5个小朋友吃了2盒饼干,每盒4千克。
(1)平均每个小朋友吃了几分之几盒饼干?
(2)平均每个小朋友吃了这些饼干的几分之几?
参考答案:
1.1.65米
【分析】可以设大猩猩的身高为x米,由于大猩猩的身高+4.35=长颈鹿的身高,据此即可列出方程,再根据等式的性质求解即可。
【详解】解:设大猩猩的身高是x米。
x+4.35=6
x=6-4.35
x=1.65
答:大猩猩的身高是1.65米。
【点睛】本题主要考查列方程解应用题,关键是找准等量关系是解题的关键。
2.双打:5张,单打:7张
【分析】设进行双打比赛的乒乓球桌有x张,则进行单打比赛的乒乓球桌有(12-x)张;双打4人比赛,x张桌有4x人,单打比赛有2人,单打人数有2×(12-x)人,双打比单打多6人,即双打比赛人数-单打比赛人数=6,列方程:4x-2×(12-x)=6,解方程,即可解答。
【详解】解:设进行双打比赛乒乓球桌有x张,则进行单打比赛乒乓球桌有(12-x)张。
4x-2×(12-x)=6
4x-24+2x=6
6x=6+24
6x=30
x=30÷6
x=5
单打:12-5=7(张)
答:进行双打比赛的乒乓球桌5张,单打比赛的乒乓球桌7张。
【点睛】本题考查方程的实际应用,利用单打桌张数与双打桌张数之间的关系,设出未知数,再根据双打人数与单打人数,找出它们之间相关的量,列方程,解方程。
3.(1)桃树的棵数-梨树的棵数=60
(2)梨树有15棵;桃树有75棵
【分析】根据题意“桃树的棵数是梨树的5倍”设梨树有x棵,则桃树有5x棵,由“桃树的棵数是梨树的5倍,比梨树多60棵”可知:桃树的棵数-梨树的棵数=60,据此列方程解答。
【详解】(1)桃树的棵数-梨树的棵数=60
(2)解:设梨树有x棵,则桃树有5x棵。
5x-x=60
4x=60
x=15
15+60=75(棵)
答:梨树有15棵,桃树有75棵。
【点睛】此题主要考查了列方程解应用题,弄清题意,找出合适的等量关系,进而列出方程是解答此类问题的关键。
4.5个
【分析】根据题意可得等量关系式:篮球的总价+足球的总价=815元,然后列方程解答即可。
【详解】解:设王老师买了x个足球。
55×8+75x=815
440+75x=815
75x=375
x=5
答:王老师买了5个足球。
【点睛】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题。
5.我选择的问题是:问题一。平城区志愿者人数×2倍-0.2万=0.36万;0.28万名。
【分析】问题一:根据题意,设平城区志愿者有x万名,云冈区有0.36万名志愿者参加,根据云冈区比比平城区志愿者人数的2倍少0.2万名,即可得到方程(2x-0.2)=0.36,然后解方程,即可得到平城区志愿者有多少万名;
问题二:已知云州区志愿者比新荣区多0.18万名,云州区的人数是新荣区的1.5倍。设新荣区志愿者有y万名,可得出方程:1.5y-y=0.18。
【详解】我选择的问题是:问题一。
平城区志愿者人数×2倍-0.2万=0.36万
解:设平城区志愿者有x万名。
2x-0.2=0.36
2x-0.2+0.2=0.36+0.2
2x÷2=0.56÷2
x=0.28
答:平城区志愿者有0.28万名。
我选择的问题是问题二:云州区志愿者有多少万名?
云州区志愿者人数-新荣区志愿者人数=0.18
解:设新荣区志愿者有y万名。
1.5y-y=0.18
0.5y=0.18
0.5y÷0.5=0.18÷0.5
y=0.36
0.36×1.5=0.54(万名)
答:云州区志愿者有0.54万名。
【点睛】利用方程解决问题的关键是找准题目中的等量关系。
6.60千米
【分析】根据题意,经过3小时,小汽车行驶80×3=240千米,用240-30=210千米,求出两地的一半的距离是210千米,再用210×2,求出两地的距离;设摩托车每小时行x千米,摩托车3小时行3x千米,小汽车3小时行80×3千米,摩托车行驶的路程+小汽车行驶的路程=两地的距离,列方程:3x+80×3=(80×3-30)×2,解方程,即可解答。
【详解】解:设摩托车每小时行x千米。
3x+80×3=(80×3-30)×2
3x+240=(240-30)×2
3x+240=210×2
3x+240=420
3x=420-240
3x=180
x=180÷3
x=60
答:摩托车每小时行60千米。
【点睛】本题考查方程的实际应用,利用速度、时间和距离三者关系,设出未知数,找出相关的量,列方程,解方程,关键是求出两地之间的距离。
7.文艺书:256本;科技数64本
【分析】设科技书有x本,则文艺书有4x本;根据文艺书和科技书共320本列出方程求出科技书的本数,进而得出文艺书的本数;据此解答。
【详解】解:设科技书有x本,则文艺书有4x本。
x+4x=320
5x=320
5x÷5=320÷5
x=64
4x=4×64=256
答:文艺书有256本,科技数有64本。
【点睛】本题主要考查列方程解含有两个未知数的问题,找出等量关系式是解题的关键。
8.儿童票:22.5元;成人票:45元
【分析】根据题意,儿童票是成人票的一半,设儿童票为x元,则成人票为2x元,5个大人,票价为(2x×5)元;2个孩子,2个孩子票价为2x元;一共付门票270元,即2个孩子票价钱+5个大人票价=270元,列方程:2x+2x×5=270,解方程,求出儿童票价钱,进而求出成人票价。
【详解】解:设儿童票x元,则成人票2x元。
2x+2x×5=270
2x+12x=270
12x=270
x=270÷12
x=22.5
成人票:22.5×2=45(元)
答:花博园的儿童票22.5元,成人票45元。
【点睛】根据方程的实际应用,利用儿童票价与成人票价之间的关系,设出未知数,找出相关的量,列方程,解方程。
9.小玲:30张;小宁:60张;小亮:90张
【分析】设小玲有邮票x张;小宁的邮票是小玲的2倍,小宁有邮票2x张,小亮的邮票是小玲和小宁的邮票的和,即小亮有邮票(x+2x)张,他们共有邮票180张,列方程:x+2x+(x+2x)=180,解方程,即可解答。
【详解】设小玲有邮票x张,则小宁有邮票2x张,小亮有邮票x+2x张。
x+2x+(x+2x)=180
3x+3x=180
6x=180
x=180÷6
x=30
小宁:30×2=60(张)
小亮:30+30×2
=30+60
=90(张)
答:小玲有邮票30张,小宁有邮票60张,小亮有邮票90张。
【点睛】本题考查方程的实际应用,根据小玲、小宁、小亮三人邮票张数之间的关系,设出未知数,找出相关的量,列方程,解方程。
10.(1)刘超在上课第10分钟开始心跳逐渐加快,在第25分钟时达到最快,之后又开始下降;邓波的心跳在上课第5分钟开始加快,在第15分钟时达到每分钟100次,之后又开始下降,第20分钟时达到每分钟90次,之后又开始加快,在第30分钟时达到最快,之后又急剧下降。
(2)刘超从第10分钟开始运动,在第25分钟时停止运动,(不唯一)
【分析】(1)根据折线统计图,依次对两个人进行分析上升表示心跳加快,下降表示心跳减慢,分段分析即可。(2)线段上升表示在运动,线段下降表示运动减慢或停止运动,据此任找一人分析即可。
【详解】(1)刘超在上课第10分钟开始心跳逐渐加快,在第25分钟时达到最快,之后又开始下降;邓波的心跳在上课第5分钟开始加快,在第15分钟时达到每分钟100次,之后又开始下降,第20分钟时达到每分钟90次,之后又开始加快,在第30分钟时达到最快,之后又急剧下降。
(2)刘超从第10分钟开始运动,在第25分钟时停止运动,(不唯一)
【点睛】此题要求学生自己描述折线统计图中体现的相关信息,难度相对较大,注意语言表述的准确性。
11.(1)图见详解
(2)500;
(3)1050;下降;
(4)9200;上升;
(5)见详解
【分析】(1)根据表中的数据完成复式折线统计图即可;
(2)从统计图可知,纵轴从0到500,即可得知一个单位长度;
(3)用台式电脑上半年6个月的制造总台数除以6得出平均台数,根据折线图走势可知月产量趋势;
(4)将笔记本电脑上半年6个月的制造台数相加即可,根据折线图走势可知月产量趋势;
(5)根据统计图台式电脑和笔记本电脑的生产趋势,进行解答,合理即可。
【详解】(1)如下图:
(2)纵轴上一个单位长度表示500台;
(3)(1500+1200+1000+1000+850+750)÷6
=6300÷6
=1050(台)
根据统计图可知,台式电脑月产量呈下降趋势;
(4)500+1000+1200+1500+2000+3000
=2700+6500
=9200(台)
根据统计图可知,笔记本电脑月产量呈上升趋势;
(5)答:台式电脑的产量逐步下降,笔记本电脑的产量不断上升,且笔记本电脑的产量已经远超过台式电脑的产量,表明笔记本电脑的市场需求量远大于台式电脑。在生产的安排上可以适当多生产笔记本电脑,少生产台式电脑,避免过多剩余(言之有理即可)。
【点睛】解答此题的关键利用图中已知的信息,结合给出的条件,求得各部分数据解决问题;需要熟练掌握平均数=总量÷份数的平均数公式。
12.(1)1
(2)20℃
(3)这一天从8:00~16:00的气温先上升后下降。
【分析】(1)根据点的间隔,观察统计图横轴填空;
(2)将所有温度加起来÷9即可;
(3)根据折线的趋势作答即可。
【详解】(1)小红每隔( 1 )小时测量一次气温。
(2)(16+17+19+20+22+23+23+21+19)÷9
=180÷9
=20(℃)
这一天的平均气温是( 20℃ )。
(3)这一天从8:00~16:00的气温先上升后下降。
【点睛】本题考查了折线统计图的应用和分析,平均数=总数÷份数。
13.(1)甲:80;乙:80。
(2)选乙参加,因为甲乙两人成绩的平均数相等,但乙的成绩方差小,故比较稳定。
【分析】(1)根据平均数的计算方法,结合折线图读出数据可得答案。
(2)根据折线图,由于两人的平均数相等,即总体水平相同,再比较方差,选方差小的参加。
【详解】(1)甲平均数:(65+80+80+85+90)÷5=400÷5=80;
乙平均数:(70+90+85+75+80)÷5=400÷5=80;
答:甲学生5次测验的平均成绩80分,乙学生5次测验的平均成绩80分。
(2)甲方差:[(65-80)+(80-80)+(80-80)+(85-80)+(90-80)]÷5
=(225+25+100)÷5
=350÷5
=70
乙方差:[(70-80)+(90-80)+(85-80)+(75-80)+(80-80)]÷5
=(100+100+25+25)÷5
=250÷5
=50
70>50
答:由以上可知,甲乙两人成绩的平均数相等,但乙的成绩方差小,故比较稳定,故选乙参加。
【点睛】本题考查平均数、方差的计算及折线统计图的运用,折线统计图表示的是事物的变化情况,在做的过程中要注意细节。
14.8月17日
【分析】小林每6天游泳一次,小军每8天游泳一次,6和8的最小公倍数就是他们相遇两次之间间隔的时间;从7月24日向后推算这个天数即可。
【详解】6=2×3,8=2×2×2,6和8的最小公倍数是:2×2×2×3=24,所以他们每相隔24天见一次面;7月24日再过24天是8月17日。
答:8月17日他们又再次相遇。
【点睛】本题关键是找出他们每两次相遇之间相隔的天数,进而根据开始的天数推算求解。
15.边长60cm的地砖正好铺满,理由见解析。
【分析】根据题意可以计算出卫生间的总面积,除以地砖面积,没有余数说明正好铺满,有余数说明不能正好铺满。
【详解】300×240=72000(平方厘米)
50×50=2500(平方厘米)
72000÷2500=28(块)……2000(平方厘米)
边长为50厘米时,有余数,不能正好铺满。
60×60=3600(平方厘米)
72000÷3600=20(块)
边长为50厘米时,没有余数,能正好铺满。
答:边长60cm的地砖正好铺满。需要用20块。
【点睛】此题还可以从另一个角度思考:装好铺满,说明地砖的边长是300和240的公因数,据此可以推断正好铺满的是边长60厘米的地砖。
16.60人
【分析】求出三种站法每排人数的最小公倍数就是最少人数。
【详解】4=2×2
6=2×3
2×2×3×5=60(人)
答:五年级(2)班至少有学生60人。
【点睛】全部公有的质因数和各自独立的质因数,它们连乘的积就是这几个数的最小公倍数。
17.61粒
【分析】由题意可知:糖果的数量是3、4、5的公倍数+1
【详解】3、4、5的最小公倍是60
60+1<100
所以这包糖果共有61粒。
答:这包糖果共有61粒。
【点睛】本题主要考查公倍数的实际应用。
18.34棵;68棵
【分析】(1)要求最少要栽多少棵,即每相邻两棵树之间的距离最大,即相邻两棵树之间的距离是60和42的最大公因数,求出60和42的最大公因数,即相邻两棵树之间的距离,即可求出应栽树的棵数;
(2)因为此长方形的池塘四周及四角栽柳树,可以看成是一个封闭的图形,所栽的柳树的棵数和间距数相等,用间距乘2即可解答出所种的桃树的棵数。
【详解】60=2×2×3×5
42=2×3×7
60、42的最大公因数是2×3=6
(60+42)×2÷6
=102×2÷6
=204÷6
=34(棵)
34×2=68(棵)
答:最少要种14棵柳树,桃树一共栽了68棵。
【点睛】关键是理解题意,明白是从求公因数作为突破口,进而找出解决问题的方法。
19.(1)60厘米
(2)20个
【分析】(1)由题意知:拼成的大正方形的边长既是15的倍数,也是12的倍数。求得15和12的最小公倍数既是大正方形的边长。
(2)在大正方形中,一行可以摆60÷15=4个小长方形,一共可以摆60÷12=5行,所以一共可以摆4×5=20(个)
【详解】(1)15=3×5
12=2×2×3
15和12的最小公倍数是:2×2×3×5=60
答:这个大正方形的边长最少60厘米。
(2)60÷15=4(个)
60÷12=5(行)
4×5=20(个)
答:至少需要20个这样的小长方形。
【点睛】明确大正方形的边长是小长方形长和宽的最小公倍数,再求得大正方形中一行可以摆几个,可以摆几行是解答本题的关键。
20.1米;
【分析】减了4次就是剪成5段,求每段的长度,用除法即可;求每段占全长的几分之几,是把这根彩带的长度看作单位“1”,把它平均分成5份,每份占全长的。
【详解】5÷5=1(米)
1÷5=
答:每段长1米,每段占全长的。
【点睛】本题是一道易错题,主要考查对分数意义的理解。
21.
【分析】根据题意可知,1红2黄1绿4个颜色排列为一组循环,那么用57÷4即可求出几组循环和剩余几面彩旗,这样分别求出红色和绿色的彩旗数量,再根据求一个数是另一个数的几分之几用除法即可解答。
【详解】57÷4=14(组)……1(面)
红色彩旗:14×1+1=15(面)
绿色彩旗:14×1=14(面)
14÷15=
答:绿色彩旗是红色彩旗的。
【点睛】此题考查了学生对周期问题的理解与应用,以及求一个数是另一个数的几分之几的应用解法。
22.千克;千克
【分析】求1千克花生油所用花生重量,用花生重量除以花生油重量;求1千克花生所用花生油重量,用花生油重量除以花生重量。
【详解】(1)100÷42=(千克)
答:平均1千克花生油要用千克花生。
(2)42÷100=(千克)
答:用1千克花生可以榨千克花生油。
【点睛】此题主要考查学生对分数应用的实际解题能力。注意区分两问的不同:求榨油一千克油需要花生的重量是把花生的重量平均分;求每千克花生榨油的重量是把油重量平均分。
23.
【分析】求一个数是另一个数的几分之几,用除法,即用已修的路除以全长即可。
【详解】225÷500=
答:已修了全长的。
【点睛】此题主要考查学生对分数的实际应用解题能力,需要掌握求一个数是另一个数的几分之几,用除法。
24.(1)15千克
(2)箱
【分析】(1)用这3箱饼干的重量除以班级个数,即可求出每个班分到多少千克;
(2)用饼干箱数除以班级个数,即可求出每个班分到多少箱。
【详解】(1)60÷4=15(千克)
答:每个班分到15千克。
(2)3÷4=(箱)
答:每个班分到箱。
【点睛】考查了除法的意义,分数与除法的关系,学生要理解掌握。
25.(1)盒
(2)
【分析】(1)用饼干总盒数除以总人数就是平均每个小朋友吃了几分之几盒饼干;
(2)把饼干总质量看作单位“1”,用1除以总人数就是平均每个小朋友吃了这些饼干的几分之几。
【详解】(1)2÷5=(盒)
答:平均每个小朋友吃了盒饼干。
(2)1÷5=
答:平均每个小朋友吃了这些饼干的。
【点睛】解答本题要区分:第一问求的是数量;第二问求的是分率。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
