第1-3单元能力提升卷-数学五年级下册苏教版(含解析)
文档属性
| 名称 | 第1-3单元能力提升卷-数学五年级下册苏教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 518.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-06 15:28:55 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第1-3单元能力提升卷-数学五年级下册苏教版
一、选择题
1.下列的几个式子中,( )不是方程。
A.12-x>7 B.7-3a=1 C.9m+2=11 D.2x-x=0.6
2.王阿姨家在三块菜地里种了1000棵番茄,第一块菜地里种的番茄比第二块少50棵,第三块菜地里种的番茄比第二块多150棵。第二块菜地里种番茄( )棵。
A.450 B.350 C.300 D.250
3.轩轩养的小鱼数量是优优的一半,如果优优送给轩轩6条,他们的小鱼数量就一样多了,轩轩原来有多少条小鱼?设轩轩原来有x条小鱼,列方程是( )。
A.2x-x=6 B.2x+x=6+6 C.2x+x=6 D.2x-6=x+6
4.小军家和小玲家到王城公园全程都是10千米,星期天小玲和小军相约沿同一路线骑车前往,小玲比小军先出发,他俩所行的路程和时间的关系如图所示。下面说法正确的是( )。
A.他们同时到达王城公园 B.小玲在骑行途中休息了1小时
C.他们都骑行了10千米 D.他们在中途相遇了2次
5.二十四节气是中国古代劳动人民长期经验积累的结晶,它与白昼时长密切相关。春分、秋分时,昼夜时长大致相等。夏至时,白昼时长最长。下图是某地区一年中部分节气所对应的白昼时长示意图。在下列四个节气中,( )的白昼时长超过了13小时。
A.立春 B.小暑 C.秋分 D.冬至
6.如果用●代表一个不等于0的数字,用★表示0,下面组成的四位数中,一定是2、3、5的公倍数的是( )。
A.●★●★ B.●●★★ C.●★●● D.●●●★
二、填空题
7.下面哪些式子是方程?是方程的在括号里画“√”,不是的画“×”。
9+7=16( ) 3.5+2.8=6.3( ) 4.5+3=16.5( )
5a-3.5=13( ) 23-11>10( ) 7×4=28( )
8.在括号里填上“>”“<”或“=”。
(1)当x=12时,4.5x+29( )84。
(2)当m=6.4时,2.5m-m( )33.6。
9.根据图中所表示的数量关系,填一填。
“?”处应该有( )个,如果=3.6,那么=( ),=( )。
10.只填质数:12=( )+( );105=( )×( )×( )。
11.如果5m=n(m和n是不等于0的自然数),那么m和n的最大公因数是( ),最小公倍数是( )。
12.如图是小嘉和小琳跳远成绩统计图。
(1)小嘉和小琳第1次跳远的成绩相差( )m。
(2)小嘉和小琳第( )次成绩相同,第( )次成绩相差最多。
(3)小嘉的成绩呈( )趋势。
(4)( )的成绩好些。小琳第( )次进步最多。
三、判断题
13.若x+2.6=7.6,则1.5x<7.5。( )
14.若5a=5b,则a-20=b-20。( )
15.3的倍数不一定是9的倍数。( )
16.某医院要反映每天的疫苗接种人数变化情况,应选用折线统计图。( )
17.复式折线统计图可以表示两个或两个以上数量的变化情况。( )
四、计算题
18.直接写得数。
0.9×3= 3.6÷0.6= 50×0.2= 5.4÷0.9=
7.5×8= 1.8x+4.8x= 2.8a-1.9a= 2.4÷1.2=
19.解方程
(1)x÷0.26=0.52 (2)9x-2x=21.7
(3)3.18×2-2x=4.26 (4)0.25x+3.75=12
20.看图列方程并解答。
五、解答题
21.“六一”儿童节期间,李老师要将一根长24分米的黄彩带和一根长42分米的红彩带,剪成同样长的整分米数的短彩带,且没有剩余。
(1)每根短彩带最长是多少分米?
(2)一共可以剪成几根这样的短彩带?
22.某社区广场舞队由60人组成,跳舞时要排成一个长方形的队形,要求每行或每列的人数都不能少于5人,共有几种排法?试着写一写。
23.学校买来8个足球和6个排球,一共用去1080元。已知每个足球的价格都是排球的3倍,每个足球和每个排球分别是多少元?
24.有两桶油,甲桶油的质量是乙桶油的1.5倍。现在从甲桶中取出12.8千克,从乙桶中取出4.8千克,两桶中剩下油的质量正好相等,原来甲、乙两桶中各有多少千克油?
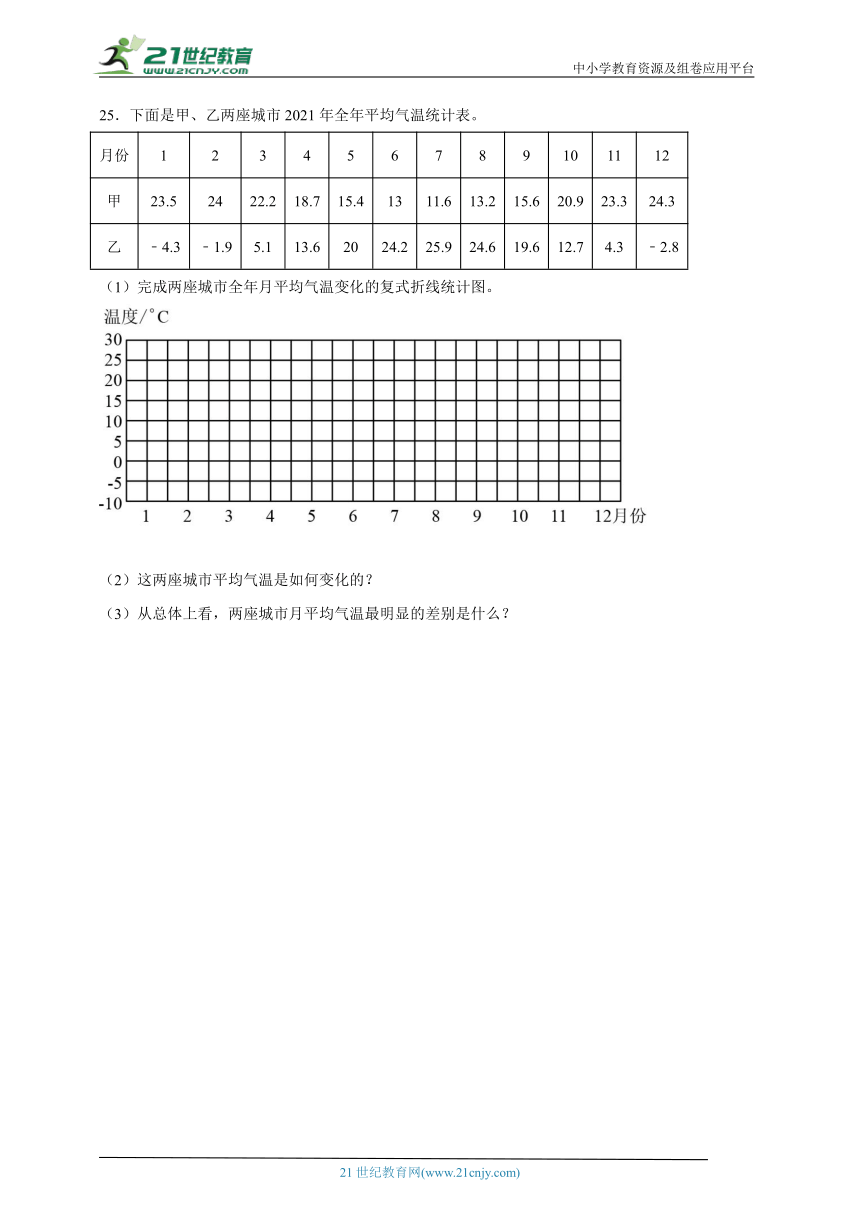
25.下面是甲、乙两座城市2021年全年平均气温统计表。
月份 1 2 3 4 5 6 7 8 9 10 11 12
甲 23.5 24 22.2 18.7 15.4 13 11.6 13.2 15.6 20.9 23.3 24.3
乙 ﹣4.3 ﹣1.9 5.1 13.6 20 24.2 25.9 24.6 19.6 12.7 4.3 ﹣2.8
(1)完成两座城市全年月平均气温变化的复式折线统计图。
(2)这两座城市平均气温是如何变化的?
(3)从总体上看,两座城市月平均气温最明显的差别是什么?
参考答案:
1.A
【分析】根据方程的定义:含有未知数的等式,可知道在方程中既要有未知数,还要是等式,据此可判断各选项正误,进而得出答案。
【详解】A.12-x>7,含有未知数x但不是等式,则这个式子不是方程;
B.7-3a=1,含有未知数a,且这个式子是等式,则是方程;
C.9m+2=11,含有未知数m,且这个式子是等式,则是方程;
D.2x-x=0.6,含有未知数x,且这个式子是等式,则是方程。
故答案为:A
2.C
【分析】设第二块菜地种的番茄是x棵,则第一块种了(x-50)棵,第三块种了(x+150)棵,根据题意可得方程:x+(x-50)+(x+150)=1000,解答求出第二块种的棵数。
【详解】解:设第二块菜地种的番茄是x棵,则第一块种了(x-50)棵,第三块种了(x+150)棵,则:
x+(x-50)+(x+150)=1000
x+x-50+x+150=1000
3x+100=1000
3x+100-100=1000-100
3x=900
3x÷3=900÷3
x=300
第二块种了300棵。
故答案为:C
3.D
【分析】设轩轩原来有x条小鱼,则优优原来的小鱼数量是2x,根据数量关系:优优原来的小鱼数量减去6等于轩轩原来的小鱼数量加上6,据此列出方程即可。
【详解】解:设轩轩原来有x条小鱼,则优优原来的小鱼数量是2x。
如果优优送给轩轩6条,则优优现在的小鱼数量是(),轩轩现在的小鱼数量是(),他们现在的小鱼数量一样多,因此列方程是:。
故答案为:D
4.C
【分析】观察折线统计图可知,实线代表小玲的行程,虚线代表小军的行程。根据统计图上的信息,逐项分析。
【详解】A.小玲是在9:00到达王城公园,而小军是在8:50到达王城公园,小军先到达,所以选项说法错误;
B.水平线是小玲休息的时间,小玲在骑行中,休息了8:30-8:20=10分钟;所以选项说法错误;
C.小军和小玲到达王城公园,都骑行了10千米,选项说法正确;
D.他们在途中遇见一次,所以选项说法错误。
故答案为:C
5.B
【分析】观察统计图,横轴表示节气名称,竖轴表示白昼时长,在图中找到相应节气,再找到对应白昼时长即可选择。
【详解】A.立春白昼不到11小时;
B.小暑白昼超过14小时;
C.秋分白昼不到13小时;
D.冬至白昼不到10小时。
故答案为:B
6.D
【分析】
2的倍数特征:个位上是0、2、4、6、8的数。
5的倍数特征:个位上是0或5的数。
2、5的倍数特征:个位上是0的数。
3的倍数特征:一个数各位上的数的和是3的倍数,这个数就是3的倍数。
【详解】设●=1;
A.●★●★,这个数是1010,1+0+1+0=2,这个数不是3的倍数,不符合题意;
B.●●★★,这个数是1100,1+1+0+0=2,这个数不是3的倍数,不符合题意;
C.●★●●,这个数是1011,1+0+1+1=3,这个数是3的倍数,但个位上是1,不是2、5的倍数,不符合题意;
D.●●●★,这个数是1110,1+1+1+0=3,这个数是3的倍数,且个位上是0,所以这个数一定是2、3、5的公倍数,符合题意。
故答案为:D
7. × × √ √ × ×
【分析】
含有未知数的等式叫做方程。
根据方程的意义可知,方程必须满足两个条件:一是含有未知数;二是等式;据此判断。
【详解】9+7=16,是等式,但不含未知数,所以不是方程。(×)
3.5+2.8=6.3,是等式,但不含未知数,所以不是方程。(×)
4.5+3=16.5,既含有未知数,又是等式,所以是方程。(√)
5a-3.5=13,既含有未知数,又是等式,所以是方程。(√)
23-11>10,既不含未知数,又不是等式,所以不是方程。(×)
7×4=28,是等式,但不含未知数,所以不是方程。(×)
8.(1)<
(2)<
【分析】(1)把x=12代入4.5x+29中,再将计算结果与84比较;
(2)把m=6.4时代入2.5m-m中,将计算结果与33.6比较即可。
【详解】(1)x=12时
4.5x+29
=
=
=
(2)m=6.4时
2.5m-m
=1.5m
=
=9.6
9.6(<)33.6
【点睛】
9. 6 1.8 10.8
【分析】
由图知:一个等于2个,一个等于3个,据此数量关系,可求得当如果=3.6时及的值。
【详解】左图:4÷2=2
一个等于2个
中图:因一个等于3个
3×2=6
所以一个等于6个白球。
当=3.6,
=3.6÷2=1.8
一个等于3个
=3.6×3=10.8
10. 5 7 3 5 7
【分析】在自然数中,除了1和它本身外,没有别的因数的数为质数,比如3,只有1和它本身这两个因数,所以3是质数,据此意义将题目中的数据分解成质数相加或者相乘的形式即可。
【详解】由分析可得:
12=5+7(两个加数顺序可以改变);
105=3×5×7(因数顺序可以改变)。
11. m n
【分析】
成倍数关系的两个数,较大数是这两个数的最小公倍数,较小数是这两个数的最大公因数。因为5m=n,说明n是m的倍数,并且n>m,那么m和n的最大公因数是m,最小公倍数是n。
【详解】如果5m=n(m和n是不等于0的自然数),那么m和n的最大公因数是m,最小公倍数是n。
12.(1)0.1
(2) 2 4
(3)上升
(4) 小嘉 5
【分析】
(1)小嘉第一次跳远成绩是2.3米,小琳第一次跳远成绩是2.4米,相减即可解答;
(2)相同次数对应的点重合,则成绩相同;相同次数对应的点距离越远,则成绩相差最多;
(3)折线向上表示成绩上升,折线向下表示成绩下降,据此解答
(4) 一条折线在另一条折线上方时,这条折线代表的成绩较好,折线向上越抖,进步越大,据此解答。
【详解】(1)2.4-2.3=0.1(米)
(2)小嘉和小琳第2次对应的点重合,成绩相同。
第1次:2.4-2.3=0.1(m)
第2次:2.5-2.5=0(m)
第3次:2.7-2.6=0.1(m)
第4次:2.8-2.5=0.3(m)
第5次:2.9-2.75=0.15(m)
0.3>0.15>0.1>0
因此小嘉和小琳第2次成绩相同,第4次成绩相差最多。
(3)小嘉的成绩呈上升趋势。
(4)小嘉的成绩分别是:2.3m、2.5m、2.7m、2.8m、2.9m
2.5-2.3=0.2
2.7-2.5=0.2
2.8-2.7=0.1
2.9-2.8=0.1
小琳的成绩分别是:2.4m、2.5m、2.6m、2.5m、2.75m
2.5-2.4=0.1(m)
2.6-2.5-0.1(m)
2.75-2.5=0.25(m)
小嘉的成绩好些。小琳第5进步最多。
13.×
【分析】先解方程x+2.6=7.6,然后计算出1.5x的值,看结果是否小于7.5即可。
【详解】x+2.6=7.6
x+2.6-2.6=7.6-2.6
x=5
当x=5时,1.5x=1.5×5=7.5
原题说法错误。
故答案为:×
【点睛】本题考查了方程的解法及利用代入法求值,需熟练掌握计算方法。
14.√
【分析】根据等式的性质2,等式两边同时除以5,再根据等式的性质1,等式两边同时减20,判断即可。
【详解】5a=5b
5a÷5=5b÷5
a=b
a-20=b-20
若5a=5b,则a-20=b-20。
原题干说法正确。
故答案为:√
【点睛】数量掌握等式的性质1和性质2是解答本题的关键。
15.√
【分析】由于9是3的倍数,那么9的倍数一定是3的倍数,3的倍数中,例如6是3的倍数,但是6不是9的倍数,据此判断。
【详解】3的倍数不一定是9的倍数,如3和6是3的倍数,但不是9的倍数;所以原题说法正确。
故答案为:√。
【点睛】本题主要考查了找一个数的倍数,解题的关键是列举出3的倍数中不是9的倍数的数。
16.√
【分析】折线统计图:能够反应数量的多少,能够反映出数量的增减变化情况;条形统计图:能够清楚的反映出数量的多少,由此即可判断。
【详解】由分析可知:
某医院要反映每天的疫苗接种人数变化情况,应选用折线统计图。原题说法正确。
故答案为:√
【点睛】本题主要考查统计图的特点,熟练掌握折线统计图和条形统计图的特点并灵活运用。
17.√
【分析】复式折线统计图是用一个单位长度表示一定的数量,根据数量的多少描出各点,然后把各点用线段顺次连接起来,以折线的上升或下降来表示统计数量增减变化。复式折线统计图用于两者或两者以上比较。
【详解】根据分析可知,复式折线统计图可以表示两个或两个以上数量的变化情况,说法正确。
故答案为:√
【点睛】考查了复式折线统计图,折线统计图不仅能表示出数量的多少,还能反映出数量的变化情况。
18.2.7;6;10;6
60;6.6x;0.9a;2
【解析】略
19.(1)x=0.1352;(2)x=3.1
(3)x=1.05;(4)x=33
【分析】解方程主要运用等式的性质,等式两边同时加上或者减去同一个数,等式不变。等式两边同时乘或者除以一个不为0的数,等式不变。把含有x的放在等号的一侧,不含x的放在等号的另一侧,然后把x前的系数除过去,就能得出x是多少
【详解】(1)x÷0.26=0.52
解:x=0.52×0.26
x=0.1352
(2)9x-2x=21.7
解:7x=21.7
x=21.7÷7
x=3.1
(3)3.18×2-2x=4.26
解:6.36-2x=4.26
2x=6.36-4.26
2x=2.1
x=2.1÷2
x=1.05
(4)0.25x+3.75=12
解:0.25x=12-3.75
0.25x=8.25
x=8.25÷0.25
x=33
20.70米
【分析】首先根据一条路全长380米,已经修了3天,还剩170米没修,设每天修x米,那么已修米数为3x,已修的米数+剩下的170米=全长380米,列方程即可解答。
【详解】解:设每天修x米
3x+170=380
3x+170-170=380-170
3x=380-170
3x=210
3x÷3=210÷3
x=70
每天修70米。
21.(1)6分米;(2)11根
【分析】(1)将24和42分别分解质因数,再求出公有质因数的乘积,求出这两个数的最大公因数,即每根短彩带最长是多少分米;
(2)利用除法,分别求出黄彩带剪成了几段、红彩带剪成了几段,再利用加法求出一共可以剪成几根这样的短彩带。
【详解】(1)24=2×2×2×3
42=2×3×7
2×3=6
所以,24和42的最大公因数是6。
答:每根短彩带最长是6分米。
(2)24÷6+42÷6
=4+7
=11(根)
答:一共可以剪成11根这样的短彩带。
【点睛】本题考查了最大公因数,掌握最大公因数的求法是解题关键。
22.5和12,12和5,6和10,10和6,共4种。
【分析】根据题意可知,先找出60的因数,可以一对一对的找;因为每行或每列不得少于5人,所以60的因数中,小于5的不考虑;去掉小于5的因数,60的因数中还剩下5、6、10、12,而5×12=6×10=60,进而可确定出每行每列的人数。
【详解】60的因数有:1,2,3,4,5,6,10,12,15,20,30,60。
因为每行或每列不得少于5人,
所以行、列分别是5和12,12和5,6和10,10和6,共4种。
答:共有4种排法。
【点睛】解答本题关键是掌握找一个数的因数的方法。
23.排球:36元;足球:108元
【分析】由于足球的价格是排球的3倍,可以设排球的价格为x元,则足球的价格为:3x元,8×足球的单价+6×排球的单价=1080,据此即可列方程,再根据等式的性质解方程即可。
【详解】解:设设排球的价格为x元,则足球的价格为:3x元。
6x+8×3x=1080
6x+24x=1080
30x=1080
x=1080÷30
x=36
36×3=108(元)
答:每个排球的价格是36元,足球的价格是108元。
【点睛】此题属于含有两个未知数的应用题,这类题用方程解答比较容易,关键是找准数量间的相等关系,设一个未知数为x,另一个未知数用含x的式子表示,然后列方程解答。
24.甲桶24千克,乙桶16千克
【分析】设原来乙桶油有x千克,则原来甲桶油有1.5x千克。根据题意,原来甲桶油的质量-12.8=原来乙桶油的质量-4.8,据此列方程解答。
【详解】解:设原来乙桶油有x千克,则原来甲桶油有1.5x千克。
1.5x-12.8=x-4.8
1.5x-x=12.8-4.8
0.5x=8
x=16
甲桶油:16×1.5=24(千克)
答:原来甲桶油有24千克,乙桶油有16千克。
【点睛】列方程解含有两个未知数的问题时,设其中的一个未知数是x,用含有x的式子表示另一个未知数,再根据等量关系即可列出方程。
25.(1)见详解
(2)甲城市2-7月平均气温逐渐降低,7-12月的月平均气温逐渐升高;乙城市1-7月的月平均气温逐渐升高,7-12月的月平均气温逐渐降低。
(3)甲城市月平均气温最高时,乙城市月平均气温最低。(合理即可)
【分析】(1)根据统计表中的数据完成统计图即可;
(2)(3)观察统计图中的折线变化趋势完成作答。
【详解】(1)统计图如下:
(2)甲城市2-7月平均气温逐渐降低,7-12月的月平均气温逐渐升高;乙城市1-7月的月平均气温逐渐升高,7-12月的月平均气温逐渐降低。
(3)甲城市月平均气温最高时,乙城市月平均气温最低。
【点睛】本题主要考查了复式折线统计图的绘制,关键是根据统计图中的信息解决实际问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第1-3单元能力提升卷-数学五年级下册苏教版
一、选择题
1.下列的几个式子中,( )不是方程。
A.12-x>7 B.7-3a=1 C.9m+2=11 D.2x-x=0.6
2.王阿姨家在三块菜地里种了1000棵番茄,第一块菜地里种的番茄比第二块少50棵,第三块菜地里种的番茄比第二块多150棵。第二块菜地里种番茄( )棵。
A.450 B.350 C.300 D.250
3.轩轩养的小鱼数量是优优的一半,如果优优送给轩轩6条,他们的小鱼数量就一样多了,轩轩原来有多少条小鱼?设轩轩原来有x条小鱼,列方程是( )。
A.2x-x=6 B.2x+x=6+6 C.2x+x=6 D.2x-6=x+6
4.小军家和小玲家到王城公园全程都是10千米,星期天小玲和小军相约沿同一路线骑车前往,小玲比小军先出发,他俩所行的路程和时间的关系如图所示。下面说法正确的是( )。
A.他们同时到达王城公园 B.小玲在骑行途中休息了1小时
C.他们都骑行了10千米 D.他们在中途相遇了2次
5.二十四节气是中国古代劳动人民长期经验积累的结晶,它与白昼时长密切相关。春分、秋分时,昼夜时长大致相等。夏至时,白昼时长最长。下图是某地区一年中部分节气所对应的白昼时长示意图。在下列四个节气中,( )的白昼时长超过了13小时。
A.立春 B.小暑 C.秋分 D.冬至
6.如果用●代表一个不等于0的数字,用★表示0,下面组成的四位数中,一定是2、3、5的公倍数的是( )。
A.●★●★ B.●●★★ C.●★●● D.●●●★
二、填空题
7.下面哪些式子是方程?是方程的在括号里画“√”,不是的画“×”。
9+7=16( ) 3.5+2.8=6.3( ) 4.5+3=16.5( )
5a-3.5=13( ) 23-11>10( ) 7×4=28( )
8.在括号里填上“>”“<”或“=”。
(1)当x=12时,4.5x+29( )84。
(2)当m=6.4时,2.5m-m( )33.6。
9.根据图中所表示的数量关系,填一填。
“?”处应该有( )个,如果=3.6,那么=( ),=( )。
10.只填质数:12=( )+( );105=( )×( )×( )。
11.如果5m=n(m和n是不等于0的自然数),那么m和n的最大公因数是( ),最小公倍数是( )。
12.如图是小嘉和小琳跳远成绩统计图。
(1)小嘉和小琳第1次跳远的成绩相差( )m。
(2)小嘉和小琳第( )次成绩相同,第( )次成绩相差最多。
(3)小嘉的成绩呈( )趋势。
(4)( )的成绩好些。小琳第( )次进步最多。
三、判断题
13.若x+2.6=7.6,则1.5x<7.5。( )
14.若5a=5b,则a-20=b-20。( )
15.3的倍数不一定是9的倍数。( )
16.某医院要反映每天的疫苗接种人数变化情况,应选用折线统计图。( )
17.复式折线统计图可以表示两个或两个以上数量的变化情况。( )
四、计算题
18.直接写得数。
0.9×3= 3.6÷0.6= 50×0.2= 5.4÷0.9=
7.5×8= 1.8x+4.8x= 2.8a-1.9a= 2.4÷1.2=
19.解方程
(1)x÷0.26=0.52 (2)9x-2x=21.7
(3)3.18×2-2x=4.26 (4)0.25x+3.75=12
20.看图列方程并解答。
五、解答题
21.“六一”儿童节期间,李老师要将一根长24分米的黄彩带和一根长42分米的红彩带,剪成同样长的整分米数的短彩带,且没有剩余。
(1)每根短彩带最长是多少分米?
(2)一共可以剪成几根这样的短彩带?
22.某社区广场舞队由60人组成,跳舞时要排成一个长方形的队形,要求每行或每列的人数都不能少于5人,共有几种排法?试着写一写。
23.学校买来8个足球和6个排球,一共用去1080元。已知每个足球的价格都是排球的3倍,每个足球和每个排球分别是多少元?
24.有两桶油,甲桶油的质量是乙桶油的1.5倍。现在从甲桶中取出12.8千克,从乙桶中取出4.8千克,两桶中剩下油的质量正好相等,原来甲、乙两桶中各有多少千克油?
25.下面是甲、乙两座城市2021年全年平均气温统计表。
月份 1 2 3 4 5 6 7 8 9 10 11 12
甲 23.5 24 22.2 18.7 15.4 13 11.6 13.2 15.6 20.9 23.3 24.3
乙 ﹣4.3 ﹣1.9 5.1 13.6 20 24.2 25.9 24.6 19.6 12.7 4.3 ﹣2.8
(1)完成两座城市全年月平均气温变化的复式折线统计图。
(2)这两座城市平均气温是如何变化的?
(3)从总体上看,两座城市月平均气温最明显的差别是什么?
参考答案:
1.A
【分析】根据方程的定义:含有未知数的等式,可知道在方程中既要有未知数,还要是等式,据此可判断各选项正误,进而得出答案。
【详解】A.12-x>7,含有未知数x但不是等式,则这个式子不是方程;
B.7-3a=1,含有未知数a,且这个式子是等式,则是方程;
C.9m+2=11,含有未知数m,且这个式子是等式,则是方程;
D.2x-x=0.6,含有未知数x,且这个式子是等式,则是方程。
故答案为:A
2.C
【分析】设第二块菜地种的番茄是x棵,则第一块种了(x-50)棵,第三块种了(x+150)棵,根据题意可得方程:x+(x-50)+(x+150)=1000,解答求出第二块种的棵数。
【详解】解:设第二块菜地种的番茄是x棵,则第一块种了(x-50)棵,第三块种了(x+150)棵,则:
x+(x-50)+(x+150)=1000
x+x-50+x+150=1000
3x+100=1000
3x+100-100=1000-100
3x=900
3x÷3=900÷3
x=300
第二块种了300棵。
故答案为:C
3.D
【分析】设轩轩原来有x条小鱼,则优优原来的小鱼数量是2x,根据数量关系:优优原来的小鱼数量减去6等于轩轩原来的小鱼数量加上6,据此列出方程即可。
【详解】解:设轩轩原来有x条小鱼,则优优原来的小鱼数量是2x。
如果优优送给轩轩6条,则优优现在的小鱼数量是(),轩轩现在的小鱼数量是(),他们现在的小鱼数量一样多,因此列方程是:。
故答案为:D
4.C
【分析】观察折线统计图可知,实线代表小玲的行程,虚线代表小军的行程。根据统计图上的信息,逐项分析。
【详解】A.小玲是在9:00到达王城公园,而小军是在8:50到达王城公园,小军先到达,所以选项说法错误;
B.水平线是小玲休息的时间,小玲在骑行中,休息了8:30-8:20=10分钟;所以选项说法错误;
C.小军和小玲到达王城公园,都骑行了10千米,选项说法正确;
D.他们在途中遇见一次,所以选项说法错误。
故答案为:C
5.B
【分析】观察统计图,横轴表示节气名称,竖轴表示白昼时长,在图中找到相应节气,再找到对应白昼时长即可选择。
【详解】A.立春白昼不到11小时;
B.小暑白昼超过14小时;
C.秋分白昼不到13小时;
D.冬至白昼不到10小时。
故答案为:B
6.D
【分析】
2的倍数特征:个位上是0、2、4、6、8的数。
5的倍数特征:个位上是0或5的数。
2、5的倍数特征:个位上是0的数。
3的倍数特征:一个数各位上的数的和是3的倍数,这个数就是3的倍数。
【详解】设●=1;
A.●★●★,这个数是1010,1+0+1+0=2,这个数不是3的倍数,不符合题意;
B.●●★★,这个数是1100,1+1+0+0=2,这个数不是3的倍数,不符合题意;
C.●★●●,这个数是1011,1+0+1+1=3,这个数是3的倍数,但个位上是1,不是2、5的倍数,不符合题意;
D.●●●★,这个数是1110,1+1+1+0=3,这个数是3的倍数,且个位上是0,所以这个数一定是2、3、5的公倍数,符合题意。
故答案为:D
7. × × √ √ × ×
【分析】
含有未知数的等式叫做方程。
根据方程的意义可知,方程必须满足两个条件:一是含有未知数;二是等式;据此判断。
【详解】9+7=16,是等式,但不含未知数,所以不是方程。(×)
3.5+2.8=6.3,是等式,但不含未知数,所以不是方程。(×)
4.5+3=16.5,既含有未知数,又是等式,所以是方程。(√)
5a-3.5=13,既含有未知数,又是等式,所以是方程。(√)
23-11>10,既不含未知数,又不是等式,所以不是方程。(×)
7×4=28,是等式,但不含未知数,所以不是方程。(×)
8.(1)<
(2)<
【分析】(1)把x=12代入4.5x+29中,再将计算结果与84比较;
(2)把m=6.4时代入2.5m-m中,将计算结果与33.6比较即可。
【详解】(1)x=12时
4.5x+29
=
=
=
(2)m=6.4时
2.5m-m
=1.5m
=
=9.6
9.6(<)33.6
【点睛】
9. 6 1.8 10.8
【分析】
由图知:一个等于2个,一个等于3个,据此数量关系,可求得当如果=3.6时及的值。
【详解】左图:4÷2=2
一个等于2个
中图:因一个等于3个
3×2=6
所以一个等于6个白球。
当=3.6,
=3.6÷2=1.8
一个等于3个
=3.6×3=10.8
10. 5 7 3 5 7
【分析】在自然数中,除了1和它本身外,没有别的因数的数为质数,比如3,只有1和它本身这两个因数,所以3是质数,据此意义将题目中的数据分解成质数相加或者相乘的形式即可。
【详解】由分析可得:
12=5+7(两个加数顺序可以改变);
105=3×5×7(因数顺序可以改变)。
11. m n
【分析】
成倍数关系的两个数,较大数是这两个数的最小公倍数,较小数是这两个数的最大公因数。因为5m=n,说明n是m的倍数,并且n>m,那么m和n的最大公因数是m,最小公倍数是n。
【详解】如果5m=n(m和n是不等于0的自然数),那么m和n的最大公因数是m,最小公倍数是n。
12.(1)0.1
(2) 2 4
(3)上升
(4) 小嘉 5
【分析】
(1)小嘉第一次跳远成绩是2.3米,小琳第一次跳远成绩是2.4米,相减即可解答;
(2)相同次数对应的点重合,则成绩相同;相同次数对应的点距离越远,则成绩相差最多;
(3)折线向上表示成绩上升,折线向下表示成绩下降,据此解答
(4) 一条折线在另一条折线上方时,这条折线代表的成绩较好,折线向上越抖,进步越大,据此解答。
【详解】(1)2.4-2.3=0.1(米)
(2)小嘉和小琳第2次对应的点重合,成绩相同。
第1次:2.4-2.3=0.1(m)
第2次:2.5-2.5=0(m)
第3次:2.7-2.6=0.1(m)
第4次:2.8-2.5=0.3(m)
第5次:2.9-2.75=0.15(m)
0.3>0.15>0.1>0
因此小嘉和小琳第2次成绩相同,第4次成绩相差最多。
(3)小嘉的成绩呈上升趋势。
(4)小嘉的成绩分别是:2.3m、2.5m、2.7m、2.8m、2.9m
2.5-2.3=0.2
2.7-2.5=0.2
2.8-2.7=0.1
2.9-2.8=0.1
小琳的成绩分别是:2.4m、2.5m、2.6m、2.5m、2.75m
2.5-2.4=0.1(m)
2.6-2.5-0.1(m)
2.75-2.5=0.25(m)
小嘉的成绩好些。小琳第5进步最多。
13.×
【分析】先解方程x+2.6=7.6,然后计算出1.5x的值,看结果是否小于7.5即可。
【详解】x+2.6=7.6
x+2.6-2.6=7.6-2.6
x=5
当x=5时,1.5x=1.5×5=7.5
原题说法错误。
故答案为:×
【点睛】本题考查了方程的解法及利用代入法求值,需熟练掌握计算方法。
14.√
【分析】根据等式的性质2,等式两边同时除以5,再根据等式的性质1,等式两边同时减20,判断即可。
【详解】5a=5b
5a÷5=5b÷5
a=b
a-20=b-20
若5a=5b,则a-20=b-20。
原题干说法正确。
故答案为:√
【点睛】数量掌握等式的性质1和性质2是解答本题的关键。
15.√
【分析】由于9是3的倍数,那么9的倍数一定是3的倍数,3的倍数中,例如6是3的倍数,但是6不是9的倍数,据此判断。
【详解】3的倍数不一定是9的倍数,如3和6是3的倍数,但不是9的倍数;所以原题说法正确。
故答案为:√。
【点睛】本题主要考查了找一个数的倍数,解题的关键是列举出3的倍数中不是9的倍数的数。
16.√
【分析】折线统计图:能够反应数量的多少,能够反映出数量的增减变化情况;条形统计图:能够清楚的反映出数量的多少,由此即可判断。
【详解】由分析可知:
某医院要反映每天的疫苗接种人数变化情况,应选用折线统计图。原题说法正确。
故答案为:√
【点睛】本题主要考查统计图的特点,熟练掌握折线统计图和条形统计图的特点并灵活运用。
17.√
【分析】复式折线统计图是用一个单位长度表示一定的数量,根据数量的多少描出各点,然后把各点用线段顺次连接起来,以折线的上升或下降来表示统计数量增减变化。复式折线统计图用于两者或两者以上比较。
【详解】根据分析可知,复式折线统计图可以表示两个或两个以上数量的变化情况,说法正确。
故答案为:√
【点睛】考查了复式折线统计图,折线统计图不仅能表示出数量的多少,还能反映出数量的变化情况。
18.2.7;6;10;6
60;6.6x;0.9a;2
【解析】略
19.(1)x=0.1352;(2)x=3.1
(3)x=1.05;(4)x=33
【分析】解方程主要运用等式的性质,等式两边同时加上或者减去同一个数,等式不变。等式两边同时乘或者除以一个不为0的数,等式不变。把含有x的放在等号的一侧,不含x的放在等号的另一侧,然后把x前的系数除过去,就能得出x是多少
【详解】(1)x÷0.26=0.52
解:x=0.52×0.26
x=0.1352
(2)9x-2x=21.7
解:7x=21.7
x=21.7÷7
x=3.1
(3)3.18×2-2x=4.26
解:6.36-2x=4.26
2x=6.36-4.26
2x=2.1
x=2.1÷2
x=1.05
(4)0.25x+3.75=12
解:0.25x=12-3.75
0.25x=8.25
x=8.25÷0.25
x=33
20.70米
【分析】首先根据一条路全长380米,已经修了3天,还剩170米没修,设每天修x米,那么已修米数为3x,已修的米数+剩下的170米=全长380米,列方程即可解答。
【详解】解:设每天修x米
3x+170=380
3x+170-170=380-170
3x=380-170
3x=210
3x÷3=210÷3
x=70
每天修70米。
21.(1)6分米;(2)11根
【分析】(1)将24和42分别分解质因数,再求出公有质因数的乘积,求出这两个数的最大公因数,即每根短彩带最长是多少分米;
(2)利用除法,分别求出黄彩带剪成了几段、红彩带剪成了几段,再利用加法求出一共可以剪成几根这样的短彩带。
【详解】(1)24=2×2×2×3
42=2×3×7
2×3=6
所以,24和42的最大公因数是6。
答:每根短彩带最长是6分米。
(2)24÷6+42÷6
=4+7
=11(根)
答:一共可以剪成11根这样的短彩带。
【点睛】本题考查了最大公因数,掌握最大公因数的求法是解题关键。
22.5和12,12和5,6和10,10和6,共4种。
【分析】根据题意可知,先找出60的因数,可以一对一对的找;因为每行或每列不得少于5人,所以60的因数中,小于5的不考虑;去掉小于5的因数,60的因数中还剩下5、6、10、12,而5×12=6×10=60,进而可确定出每行每列的人数。
【详解】60的因数有:1,2,3,4,5,6,10,12,15,20,30,60。
因为每行或每列不得少于5人,
所以行、列分别是5和12,12和5,6和10,10和6,共4种。
答:共有4种排法。
【点睛】解答本题关键是掌握找一个数的因数的方法。
23.排球:36元;足球:108元
【分析】由于足球的价格是排球的3倍,可以设排球的价格为x元,则足球的价格为:3x元,8×足球的单价+6×排球的单价=1080,据此即可列方程,再根据等式的性质解方程即可。
【详解】解:设设排球的价格为x元,则足球的价格为:3x元。
6x+8×3x=1080
6x+24x=1080
30x=1080
x=1080÷30
x=36
36×3=108(元)
答:每个排球的价格是36元,足球的价格是108元。
【点睛】此题属于含有两个未知数的应用题,这类题用方程解答比较容易,关键是找准数量间的相等关系,设一个未知数为x,另一个未知数用含x的式子表示,然后列方程解答。
24.甲桶24千克,乙桶16千克
【分析】设原来乙桶油有x千克,则原来甲桶油有1.5x千克。根据题意,原来甲桶油的质量-12.8=原来乙桶油的质量-4.8,据此列方程解答。
【详解】解:设原来乙桶油有x千克,则原来甲桶油有1.5x千克。
1.5x-12.8=x-4.8
1.5x-x=12.8-4.8
0.5x=8
x=16
甲桶油:16×1.5=24(千克)
答:原来甲桶油有24千克,乙桶油有16千克。
【点睛】列方程解含有两个未知数的问题时,设其中的一个未知数是x,用含有x的式子表示另一个未知数,再根据等量关系即可列出方程。
25.(1)见详解
(2)甲城市2-7月平均气温逐渐降低,7-12月的月平均气温逐渐升高;乙城市1-7月的月平均气温逐渐升高,7-12月的月平均气温逐渐降低。
(3)甲城市月平均气温最高时,乙城市月平均气温最低。(合理即可)
【分析】(1)根据统计表中的数据完成统计图即可;
(2)(3)观察统计图中的折线变化趋势完成作答。
【详解】(1)统计图如下:
(2)甲城市2-7月平均气温逐渐降低,7-12月的月平均气温逐渐升高;乙城市1-7月的月平均气温逐渐升高,7-12月的月平均气温逐渐降低。
(3)甲城市月平均气温最高时,乙城市月平均气温最低。
【点睛】本题主要考查了复式折线统计图的绘制,关键是根据统计图中的信息解决实际问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
